Curvas Elípticas En Profundidad (Parte 1)

La criptografía está en constante evolución.

Nuevas técnicas se desarrollan todo el tiempo. Especialmente en algunos campos que parecen estar de moda últimamente, como las Pruebas de Conocimiento Cero, la Encriptación Totalmente Homomórfica, y la Criptografía Post-Cuántica.

Métodos mejores, más rápidos y más seguros están siendo constantemente investigados. La cantidad de técnicas criptográficas que existen es abrumadora.

Sin embargo, las estructuras matemáticas fundamentales sobre las que se basa este mundo de diversas técnicas son bastante invariantes.

Aunque quizás hay algunas caras nuevas como anillos polinomiales e ideales, y algunas investigaciones sobre alternativas más exóticas como los números p-ádicos.

La mayoría de los métodos criptográficos que usamos todos los días (a menudo sin siquiera notarlo) se basan en una única construcción: una curva elíptica.

Es posible que pronto se vuelvan obsoletas. Pero al menos en el futuro muy cercano, ¡no van a desaparecer!

Recientemente hablé sobre ellas en la serie Criptografía 101. A decir verdad, eso fue solo una breve y amigable descripción general del tema. Suficientemente buena como primera aproximación, pero ni de cerca la historia completa.

Esta vez, quiero intentar una inmersión más profunda en el mundo de las curvas elípticas. Hay mucho que cubrir, así que dividiré esto en varias partes.

¡Espero que lo disfrutes!

Curvas Elípticas

Naturalmente, la primera pregunta que se nos viene a la mente es ¿qué es una curva elíptica?

Sin más preámbulos, te presento — esto es una curva elíptica:

$$E: y^2 + a_1xy + a_2y = x^3 + a_3x^2 + a_4x + a_5$$

Lo que estás viendo es la ecuación general de Weierstrass para curvas elípticas — realmente es solo un polinomio cúbico (de grado tres). Nada de qué asustarse.

En general, usaremos la siguiente versión reducida, que es equivalente bajo ciertas condiciones que no cubriremos aquí:

$$E: y^2 = x^3 + ax + b$$

Y así es como se ve una curva elíptica cuando se grafica en un plano cartesiano:

Click to zoom

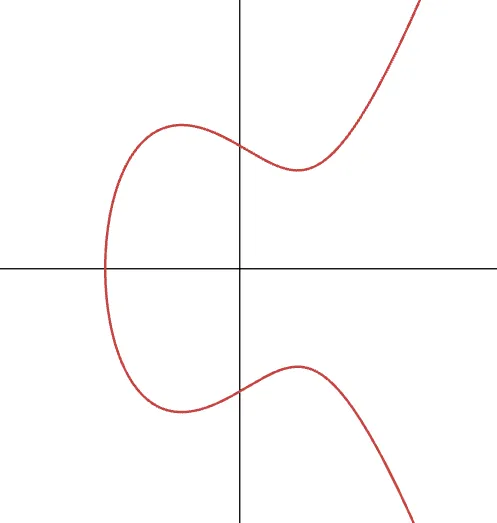
Mirando esta figura, podrías preguntarte qué hay de "elíptico" en estas curvas. Resulta que esto es en realidad un nombre inapropiado, como se explica aquí.

Lo que estamos representando aquí es la colección de puntos que satisfacen la ecuación $E$ que definimos anteriormente, al igual que una parábola satisface la ecuación $y = x^2$.

Hay un par de cosas que podemos decir sobre estas curvas desde el principio.

En primer lugar, observa cómo son simétricas respecto al eje x. Es fácil ver que el culpable es ese término $y^2$, porque cualquier valor positivo para $x^3 + ax + b$ tiene tanto una raíz cuadrada positiva como una negativa, que son ambas soluciones válidas para $y$.

En segundo lugar, la curva es suave. Sin embargo, no todas las curvas que satisfacen la expresión $E$ son suaves — como esta:

Click to zoom

Podemos ver cómo parece haber un punto de intersección. Si intentas graficar la curva $y^2 = x^3$, también notarás un comportamiento extraño.

Técnicamente no es una intersección, sino más bien dos partes puntiagudas de la curva que se tocan.

Llamamos a este tipo de curvas singulares. Las curvas singulares serán problemáticas cuando intentemos usarlas para nuestros propósitos — porque la derivada en esos puntos no está bien definida. Por esta razón, las curvas no suaves como esta no se consideran curvas elípticas.

¡Suficientes presentaciones! ¿Para qué sirven estas cosas de todos modos?

Definiendo Operaciones

Lo atractivo de estas curvas es que podemos usarlas para definir una operación. Quiero dedicar el resto de este artículo a entender dicha operación, lo que deja su utilidad fuera del panorama por ahora — pero lo cubriremos en los próximos artículos.

Aun así, me gustaría proporcionar algo de contexto antes de continuar.

Nuestra operación servirá como una pieza clave en la construcción de un grupo matemático. Hablaremos de ellos más adelante, pero la idea es que los grupos son la piedra angular para algunos problemas matemáticos extremadamente difíciles, que permiten la criptografía de clave pública que todos conocemos y amamos. Y más aún.

La operación de curva elíptica que vamos a presentar tiene una definición algo extraña. Por favor, tenme paciencia por ahora. Funciona así:

1. Elige dos puntos $P$ y $Q$ en la curva, y traza una línea a través de ellos.
2. Encontrarás que esta línea intersecta otro punto en la curva. Llamémoslo $-R$.
3. Ahora, refleja $-R$ sobre el eje x. Como $-R$ es un punto en la curva, y la curva es simétrica, llegarás a otro punto en la curva: $R$.

Todo el proceso se ve algo así:

Click to zoom

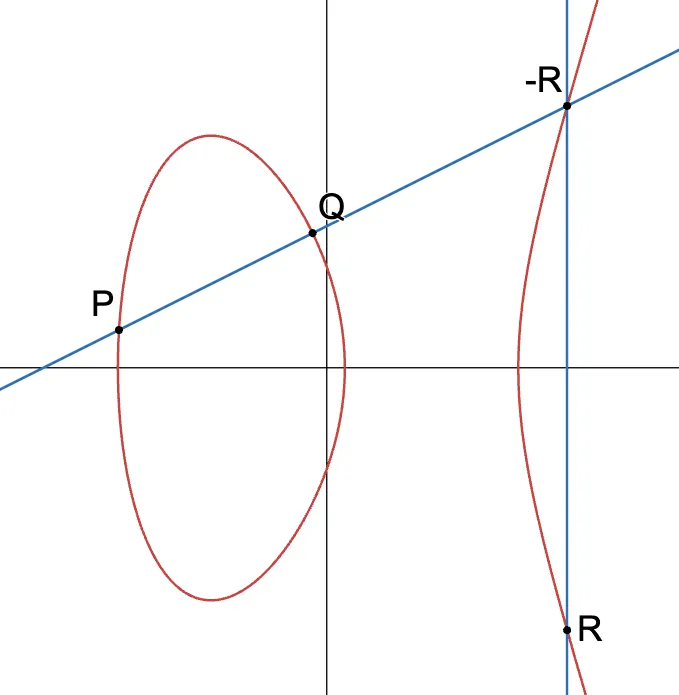
Siguiendo esta receta, hemos calculado un nuevo punto $R$ como resultado de "sumar" $P$ y $Q$. Podemos escribir esto como:

$$P \oplus Q = R$$

Es una forma extraña de definir la suma, sí, pero es útil pensar en la operación en esos términos. Usamos el símbolo $\oplus$ para diferenciarlo de la suma "normal".

Sin embargo, ¿qué sucede si queremos sumar $P$ consigo mismo?

Imaginemos, en cambio, que tenemos algún otro punto que está muy cerca de $P$ en la curva — llamémoslo $P'$. A medida que movemos $P'$ cada vez más cerca de $P$, la línea que pasa por ellos se acerca lentamente a la tangente de la curva en $P$. Muy naturalmente, podemos inferir que encontrar $P \oplus P$ se hace con el mismo proceso de antes, pero usando la tangente en $P$ como nuestra línea en el primer paso.

¡Y por eso es importante tener una primera derivada bien definida!

Para sorpresa de absolutamente nadie, la receta que seguimos se llama la regla de la cuerda y la tangente. Sin embargo, ¿siempre funciona? ¿No hay escenarios límite que puedan ser problemáticos?

El Punto de Intersección

En el paso uno de nuestra regla de la cuerda y la tangente, una suposición importante es que podemos encontrar un tercer punto de intersección. ¿Es esto siempre posible? Echemos un vistazo más de cerca — ¡es hora de algunas sustituciones!

La ecuación para una línea $l$ es muy simple:

$$l: y = mx + n$$

Lo bueno es que podemos sustituir esta expresión directamente en nuestra ecuación de curva elíptica, lo que resulta en esta igualdad polinómica de tercer grado en $x$:

$$(mx + n)^2 - x^3 - ax - b = 0$$

Un polinomio de tercer grado como este tiene como máximo tres raíces. Y como podrías adivinar, esas raíces serán las coordenadas x de los puntos donde nuestra línea intersecta la curva, si es que hay alguna intersección en absoluto.

Intentemos averiguar qué sucede cuando usamos esta expresión en los casos de la regla de la cuerda y la tangente.

La Cuerda

Si nuestro polinomio tiene tres raíces, entonces podemos factorizarlo en un producto de términos de la forma $(x - r)$. Y con un poco de reorganización, terminamos con:

$$(x - x_P)(x - x_Q)(x - x_R) = x^3 - m^2x^2 + (a - 2mn)x + b - n^2$$

Aún no hemos descubierto cuáles son los valores de $m$ y $n$, pero son bastante fáciles de calcular para una línea que pasa por dos puntos (P y Q), así que te dejaré esa parte a ti.

Es útil expandir el lado izquierdo de la expresión anterior, lo que da:

$$x^3 - (x_P + x_Q + x_R)x^2 + (x_Px_Q + x_Px_QR + x_Qx_R)x - x_Px_Qx_R$$

Y mira esto: comparando el término $x^2$ en ambos lados de la ecuación, obtenemos:

$$x_P + x_Q + x_R = m^2$$

Al mover un par de términos a la derecha, hemos obtenido una expresión para la coordenada $x$ de este tercer punto de intersección. Para encontrar $y$, todo lo que tenemos que hacer es introducirlo en la ecuación de la línea, y luego invertir el valor resultante. Y nos queda:

$$x_R = m^2 - x_P - x_Q$$ $$y_R = -(mx_R + n)$$

¡Eso es todo!

La Tangente

Encontrar $R$ es un poco más complicado ahora, porque necesitamos encontrar la línea que pasa por $P$ que es tangente a la curva. La tangente es simplemente la línea que pasa por $P$ cuya pendiente es igual a la primera derivada de la curva con respecto a $x$.

Dado que no tenemos una fórmula explícita en la forma de $E(x)$, tenemos que desempolvar nuestras habilidades de cálculo y usar un pequeño viejo truco llamado la regla de la cadena, tratando a $E(x)$ como una función implícita:

$$\frac{d}{dx}(y^2) = \frac{d}{dx}(x^3 + ax + b)$$ $$\frac{dy^2}{dy}\frac{dy}{dx} = 3x^2 + a$$ $$\frac{dy}{dx} = \frac{3x^2 + a}{2y^2}$$

Al introducir las coordenadas de $P$ en la expresión anterior, encontramos la pendiente de la línea tangente a $E$ en $P$ - este era nuestro valor $m$ en el caso anterior.

$$m = \frac{3x_P^2 + a}{2y_P^2}$$

Luego, procedemos como antes. Solo tenemos que tener cuidado de considerar $x_P$ una raíz con multiplicidad = 2. Con esto en mente, obtenemos casi exactamente el mismo resultado:

$$x_R = m^2 - 2x_P$$ $$y_R = -(mx_R + n)$$

Sumar $P$ a sí mismo es como duplicarlo. Y entonces, en lugar de escribir $P \oplus P$, escribamos $[2]P$, ¡y nos referimos a esto como - lo adivinaste - duplicación de punto!

Un Caso Extremo

¡Genial! Todo funcionando bien hasta ahora.

Ahora podríamos intentar sumar $P$ y $-P$ (su reflejo sobre el eje $x$). Sin embargo, la línea que pasa por ellos es una línea vertical, definida por $x = x_P$. Esto significa que obtendremos:

$$y_P^2 = x_P^3 + ax_P + b$$

Para un valor dado de $x_P$, esto significa que obtenemos dos valores válidos para $y_P$, no tres. No es bueno - el paso 1 de nuestro proceso requiere que exista un tercer punto de intersección. ¿O no?

Claramente, para que nuestra operación esté bien definida, necesitamos poder realizar $P \oplus (-P)$. Si esto fuera una suma simple, esto resultaría, por supuesto, en cero. Esencialmente, lo que necesitamos es definir qué significa cero para nuestra operación.

Bueno, aquí está: te presento el punto en el infinito:

$$P \oplus (-P) = \mathcal{O}$$

Click to zoom

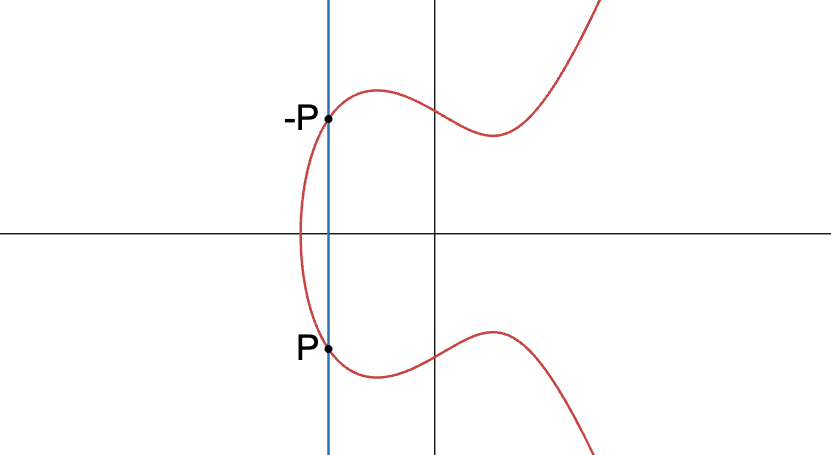
Te pido que estires un poco tu imaginación en este punto. En todo caso, piensa en esto como un "punto especial". Siempre que necesitemos sumar $P \oplus (-P)$, sabemos que la regla normal de la cuerda no se aplica y, en su lugar, sabemos que el resultado es el punto en el infinito, $\mathcal{O}$.

Le daremos más sentido a esto cuando hablemos del espacio proyectivo.

Suma Rápida

Otra cosa particularmente genial sobre esta operación que definimos es que hay un algoritmo para la suma rápida. Es decir, si quisiéramos sumar:

$$P \oplus P \oplus P \oplus ... \oplus P \oplus P = [m]P$$

Podríamos hacerlo paso a paso, sumando $P$ al resultado de cada suma subsiguiente, como ya sabemos hacer.

Sorprendentemente, podemos hacerlo mejor. Debido a que la operación es asociativa, es posible "agrupar" sumas, de una manera que podría ser conveniente para nosotros. Por ejemplo, $[5]P$ se puede escribir como:

$$[5]P = (P \oplus P) \oplus (P \oplus P) \oplus P$$ $$= [2]P \oplus [2]P \oplus P = [2]([2]P) \oplus P$$

Observa que la expresión final requiere dos duplicaciones y una suma, en contraste con las cuatro sumas requeridas en la configuración inicial. Ahorrar una sola operación puede no parecer mucho, pero cuando multiplicamos por un $m$ mayor, los ahorros son sustanciales.

El algoritmo general para la multiplicación funciona en forma de duplicar y sumar. Para cualquier entero positivo $m$ por el que queramos multiplicar, primero necesitamos encontrar su representación binaria, y hacer el siguiente proceso:

1. Establecer el valor inicial del resultado en $W = P$.
2. Luego, comenzando desde el segundo bit más significativo, asignar $W = [2]W$.
3. Si el dígito actual es un $1$, entonces también sumar $W = W \oplus P$.
4. Moverse un dígito a la derecha y repetir desde el paso $2$.

Por ejemplo, $11$ en binario es $1011$. El proceso tendría 3 iteraciones en total:

 - Inicialización: $W = P$  - Primer dígito: $W = [2]W = [2]P$  - Segundo dígito: $W = [2]W \oplus P = [5]P$  - Último dígito: $W = [2]W \oplus P = [11]P$

Un total de $3$ multiplicaciones y $2$ sumas - ya la mitad de las $10$ sumas necesarias si sumáramos un $P$ a la vez.

Típicamente, esto se llama multiplicación por $m$ en lugar de "suma rápida". Sin embargo, tenemos un algoritmo rápido y, lo que es importante, el problema inverso no es rápido en absoluto.

Con esto, quiero decir que dados dos puntos $G$ y $Q$, tales que $Q = [m]G$, no hay un algoritmo rápido para recuperar el valor de $m$.

¡Un problema tan simple es lo que permite una buena parte de la criptografía de clave pública que conocemos y amamos!

Pero ¿Por Qué Curvas Elípticas?

Vaya. Ya con las preguntas picantes.

Todavía no sabemos realmente mucho sobre cómo las curvas elípticas son útiles desde una perspectiva criptográfica. Todo lo que sabemos es cómo sumar puntos, siguiendo un proceso que, dado nuestro conocimiento actual, parece muy arbitrario y, honestamente, un poco forzado.

Por supuesto, quedan muchas cosas por decir sobre las curvas elípticas, pero al menos podemos tratar de imaginar un par de cosas.

Hay un teorema llamado teorema de Bézout que, en términos generales, dice que una línea interceptará una curva de grado tres en 3 puntos (contando el punto en el infinito y demás). Nuestra operación es entonces bastante natural: dados dos puntos en la curva, dibujar una línea a través de ellos garantiza que encontraremos un tercero, y esto es útil para obtener un resultado único.

¿Qué pasaría si intentáramos usar una curva de mayor grado? Debido al teorema de Bézout, tendríamos más de 3 puntos de intersección. Lo que significa que, si queremos sumar dos puntos $P$ y $Q$ en la curva, tendremos múltiples candidatos como resultado. ¿Cuál elegimos?

Click to zoom

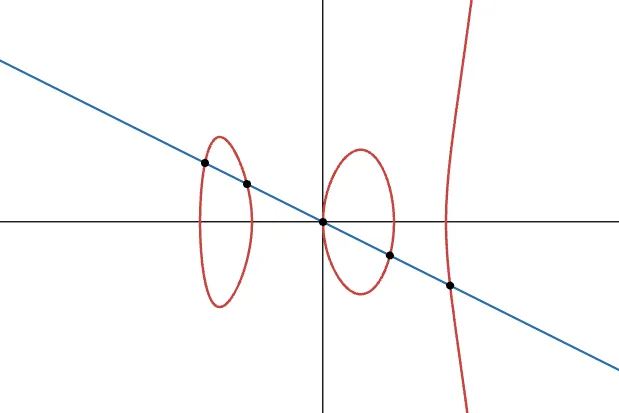
Esto hace que definir una operación sobre estos tipos de curvas sea bastante complicado.

Es posible, usando un concepto llamado divisores. Pero todavía es demasiado pronto para hablar de eso.

Si de alguna manera tuviéramos una forma de definir una operación sobre curvas de mayor grado, el otro problema que tendríamos sería la impracticidad. Encontrar expresiones para los puntos de intersección fue simple con nuestras confiables curvas elípticas, pero puede ser un lío con curvas más complejas. Es posible que ni siquiera haya fórmulas explícitas disponibles, debido al teorema de Abel-Ruffini.

Dijimos que trabajaríamos con la forma de Weierstrass, pero esto no significa que no haya otras curvas de grado tres que podríamos usar. Por ejemplo, están las curvas de Montgomery y las curvas de Edwards, que también son útiles para la criptografía, pero quizás no son las que tienen la adopción más generalizada.

Además, podríamos pensar en curvas de grado tres ligeramente más complejas, como esta:

Click to zoom

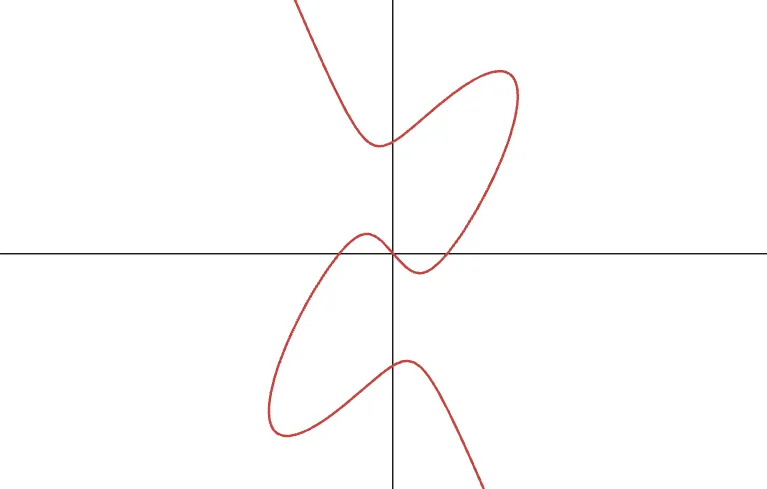
Por más que lo intentes, encontrarás que una línea intersecta esta curva como máximo en tres puntos. Pero esto no significa que sea muy práctico de usar; de hecho, las fórmulas explícitas no serán fáciles de derivar y probablemente serán más complejas computacionalmente que nuestros simples resultados de Weierstrass.

En este sentido, nuestra definición de curva elíptica se sitúa en una especie de zona "justo en el punto", equilibrando los bajos costos computacionales de las operaciones, mientras proporciona suficiente complejidad para ser útil en criptografía.

Y sobre esas fórmulas explícitas que sigo mencionando, vamos a necesitarlas con seguridad si queremos construir cualquier algoritmo a partir de nuestras curvas. Verás, estas visualizaciones son geniales como una forma de construir una comprensión inicial, pero no representan cómo se verá realmente una curva elíptica para nosotros, que se asemeja más a esto:

Click to zoom

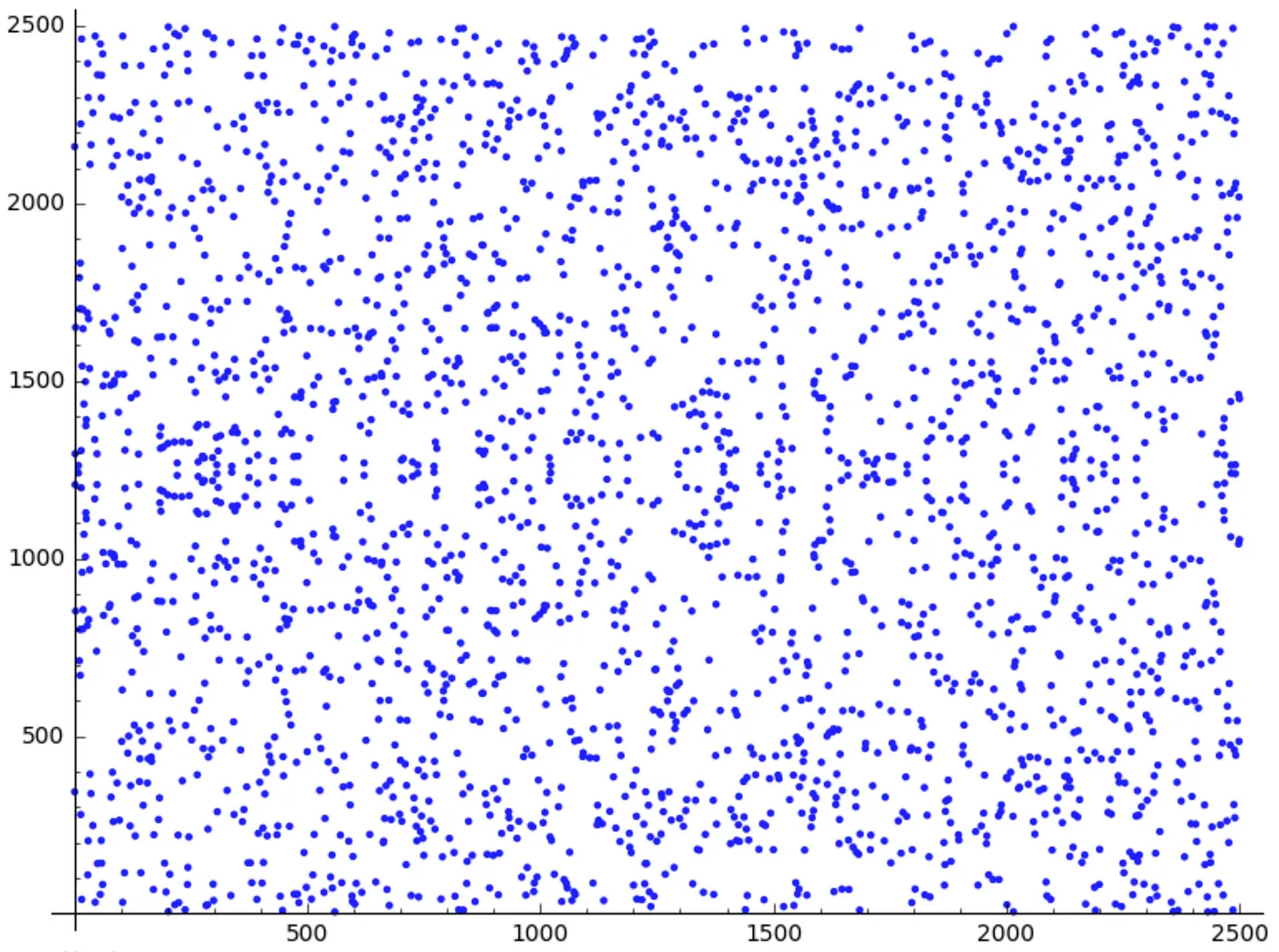
Tengo la sensación de que probablemente acabas de hacer:

No te preocupes — ¡todo tendrá sentido pronto!

Resumen

En esta primera parte de lo que (espero) será una breve serie de artículos, presentamos los conceptos básicos sobre las curvas elípticas.

Si ya leíste esto, o si tenías conocimiento previo del tema, probablemente encuentres esta introducción muy simple.

¡Pero apenas estamos comenzando! Tenemos muchas cosas divertidas por cubrir, desde problemas de millones de dólares hasta curvas en "dimensiones superiores".

Mantente despierto, ¡y te veré en la próxima parte!