Criptografía 101: Encriptación Completamente Homomórfica

Este artículo forma parte de una serie más larga sobre criptografía. Si este es el primer artículo con el que te encuentras, te recomiendo comenzar desde el principio de la serie.

Llegamos. El final del viaje.

Hemos aprendido mucho en el camino. Lo que comenzó como una simple introducción a los grupos terminó convirtiéndose en una serie completa, donde exploramos muchas ideas fundamentales en criptografía, pero también algunas técnicas que están muy cerca de ser de última generación. Estoy bastante contento con el resultado.

Sin embargo, hay un tema importante que no hemos tocado hasta ahora. No es nada menos que el santo grial de la criptografía. Y para este momento, tenemos todas las herramientas necesarias para entender cómo las técnicas modernas abordan este problema.

Eso es. Es hora de sumergirnos en la Encriptación Completamente Homomórfica.

Introducción

Homomórfico es un término que ya deberíamos conocer, ya que dedicamos un artículo completo a explicar su significado. Aún así, un breve repaso nunca viene mal.

Un homomorfismo es un tipo de función, que tiene esta simple propiedad:

$$f(a + b) = f(a) +_f f(b)$$

Nota la sutil distinción de que las operaciones no necesitan ser las mismas.

En español simple: el resultado de sumar las entradas primero y luego aplicar la función es el mismo que si invertimos el orden.

Realmente, decimos que la función es homomórfica con respecto a alguna operación, que en el escenario anterior, resulta ser la suma.

Algunos homomorfismos también son invertibles, lo que significa que para algún valor funcional $y = f(x)$, existe alguna función inversa tal que:

$$f^{-1}(y) = x$$

En este caso, la función se llama isomorfismo en su lugar.

Algunas funciones de encriptación se comportan como isomorfismos. Poder revertir la encriptación es un requisito para la funcionalidad, pero el hecho de que se comporte como un homomorfismo desbloquea algunos nuevos superpoderes.

Específicamente, puedes sumar valores encriptados, y tener la garantía de que cuando ocurra la desencriptación, obtendrás el mismo resultado que si hubieras sumado los valores no encriptados primero. Y eso es muy genial — permite que las aplicaciones realicen operaciones sobre datos encriptados, preservando así la privacidad.

Click to zoom

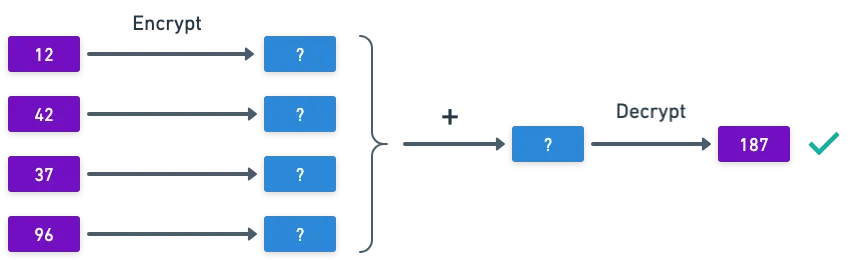
Sin embargo, hay un detalle: cuando trabajamos con grupos, solo podemos soportar una operación.

Como consecuencia, podemos crear métodos de encriptación basados en grupos que pueden manejar la suma de valores encriptados bastante fácilmente (es decir, ElGamal). ¿Pero quieres multiplicación? No. No se puede hacer eso.

Soportar la multiplicación es importante — como vimos en nuestro breve paso por circuitos aritméticos, podemos calcular casi cualquier cosa con compuertas de suma y multiplicación. Esto significa que si pudiéramos soportar ambas operaciones, ¡entonces podríamos realizar cálculos arbitrarios sobre datos encriptados, manteniendo los datos privados!

La familia de algoritmos que soportan una sola operación fue bautizada como Encriptación Parcialmente Homomórfica, o PHE.

Es importante destacar que esto podría ser suficiente para algunos tipos de aplicaciones. Por ejemplo, en caso de que solo necesitemos mantener saldos encriptados y sumar o restar de ellos, no requerimos todo el poder de FHE.

Resulta que un método que soporte tanto la suma como la multiplicación no fue fácil de concebir. Durante mucho tiempo, permaneció esquivo para los investigadores. Hubo esfuerzos como el algoritmo Boneh-Goh-Nissim, basado en emparejamientos, que podía manejar una sola multiplicación.

Simplemente no era suficiente. Soportar dos operaciones permanecía fuera de alcance.

Pero espera... ¿Dos operaciones? ¡Conocemos una mejor estructura para eso!

Encriptación Con Anillos

Los anillos suenan como la estructura algebraica que debería soportar naturalmente la encriptación completamente homomórfica. Se propusieron inicialmente esfuerzos como NTRU, pero solo podían manejar una cantidad limitada de multiplicaciones. Y hay una buena razón para esto.

En el artículo anterior, miramos Kyber, que puede usarse para encriptar mensajes cortos. Al mirar el paso de decapsulación (piensa en desencriptación), observamos que el mensaje recuperado no era exactamente el mensaje original.

Pero estaba cerca. Solo con un pequeño error. La desencriptación será posible siempre que este error se mantenga pequeño.

Esta es la idea detrás de lo que coloquialmente se llama Encriptación Algo Homomórfica, o SWHE: métodos que pueden manejar la desencriptación siempre que el error permanezca pequeño.

Y aunque Kyber no es un método de encriptación homomórfica, la idea es más o menos la misma.

Las multiplicaciones tienen una tendencia a explotar los errores, y esa es la razón por la que los métodos basados en anillos no podían soportar una cantidad ilimitada de ellas. Al menos ese era el caso, hasta que algo notable sucedió...

En 2009, Craig Gentry publicó su tesis doctoral, que introdujo un par de nuevas técnicas que desbloquearon el primer esquema verdaderamente FHE.

Como sugiere su trabajo original, la investigación comenzó con una construcción inicial, sobre la cual se aplicaron algunas técnicas que transformaron su esquema SHE base en uno FHE. ¡Creo que el mejor enfoque aquí es seguir los mismos pasos!

Construcción Base

Todo comienza con una elección adecuada de anillo. Estaremos trabajando con anillos de la forma $\mathbb{F}[X]/(f(X))$. Y también necesitamos un ideal para dicho anillo — recuerda que un ideal es un subconjunto de $R$ que es cerrado bajo suma y multiplicación por cualquier elemento de $R$:

$$x, y \in I \Rightarrow x + y \in I$$ $$x \in I, r \in R \Rightarrow r.x \in I$$

El ideal se genera aleatoriamente. Se muestrea un polinomio aleatorio $g(X)$ con coeficientes pequeños — y luego, el ideal es simplemente $(g(X))$, muy similar a como explicamos aquí.

Para continuar, debemos hablar nuevamente sobre la noción de una base. Tocamos este concepto un par de artículos atrás. En pocas palabras, una base consiste en un conjunto de vectores independientes que pueden usarse para producir cualquier punto en el retículo mediante combinación lineal. Decimos que una base genera un retículo $\Lambda$.

$$\Lambda = \left \{ \sum_{i=1}^n z_i.b_i \ | \ z_i \in \mathbb{Z} \right \}$$

Las bases para un retículo no son únicas, y hay varias bases válidas que podríamos elegir. Como ya insinuamos en artículos anteriores, hay bases buenas y bases malas — las buenas permiten resolver rápidamente el Problema del Vector Más Corto (SVP), mientras que las bases malas, aunque generan el mismo retículo, no son buenas para resolverlo eficientemente.

Click to zoom

De la imagen, podemos imaginar que una base buena debería ser un conjunto de vectores cortos, no colineales (ortogonales, si es posible). Por otro lado, las bases malas serán todo lo contrario: vectores largos, colineales.

Y así, en la construcción que estaremos viendo, se generan dos bases — sirven como las claves privada y pública para el proceso de encriptación:

$${B_J}^{sk}, {B_J}^{pk}$$

La clave secreta es una base "buena", mientras que la clave pública es una "mala".

Cabe señalar que estamos haciendo referencia a un ideal $J$ aquí, no $I$. Esto no es un error tipográfico — hay una buena razón para esto. Vamos a trabajar a través de la configuración del problema lentamente.

Realmente, todo lo que sucede es que la base mala solo es buena para calcular un valor encriptado, pero realmente ineficiente para desencriptar — mientras que la base buena permite un cálculo rápido durante la desencriptación. ¡Eso es suficiente detalle para nosotros aquí — hay otros conceptos más apremiantes para que entendamos!

Encriptación

Como de costumbre, la encriptación comienza con un mensaje. Un punto que a menudo evitamos definir claramente es a qué conjunto pertenecen los mensajes válidos — o en otras palabras, cuál es el espacio de texto plano. En nuestro caso, los valores de texto plano válidos pertenecerán al anillo cociente $R/I$. Dos cosas son notables aquí:

• Necesitamos una forma de codificar mensajes en elementos del anillo — pero podemos saltarnos esa parte por ahora.
• También necesitamos entender qué es un elemento de $R/I$. Más sobre eso en un minuto.

A continuación, y de nuevo como de costumbre, necesitamos introducir algo de aleatoriedad en nuestro esquema de encriptación. Esto asegura que cuando encriptamos el mismo valor $m$ dos veces, obtenemos dos resultados diferentes.

Se elige un nonce aleatorio del ideal $I$, con la ayuda de una base $B_i$. El texto cifrado resultante $\psi$ será el mensaje codificado original $m$, más el nonce muestreado $i$:

$$\psi = (m + i) \ \textrm{mod} \ {B_J}^{pk}$$

Usando la jerga específica de anillos, nota que $m + i$ es esencialmente un elemento aleatorio del coset $m + I$ — esto es, todos los elementos de $R$ que tienen la forma:

$$m + I = \{ m + i \ | \ i \in I\}$$

Si esto parece confuso, es porque lo es. Y como este es el último tramo de la serie, intentaré explicar esto con más detalle a través de un par de ejemplos.

Ayuda Visual al Rescate

Supongamos que estamos trabajando con el anillo $\mathbb{Z}[X]/(X^2+1)$. Cada polinomio en el anillo tendrá grado a lo sumo 1—lo que significa que podemos representar coeficientes polinomiales en un plano, como vectores 2D.

La primera coordenada corresponde al término constante, y la segunda al coeficiente de primer grado (el número multiplicando $x$).

Luego elegimos una base $B_i$ para un ideal $I$ — esto es, dos vectores que determinan un ideal. Elijamos por ejemplo los polinomios $x + 2$ y $2x - 1$; podemos asociarlos con los vectores $(2,1)$ y $(-1,2)$ en el espacio bidimensional:

Click to zoom

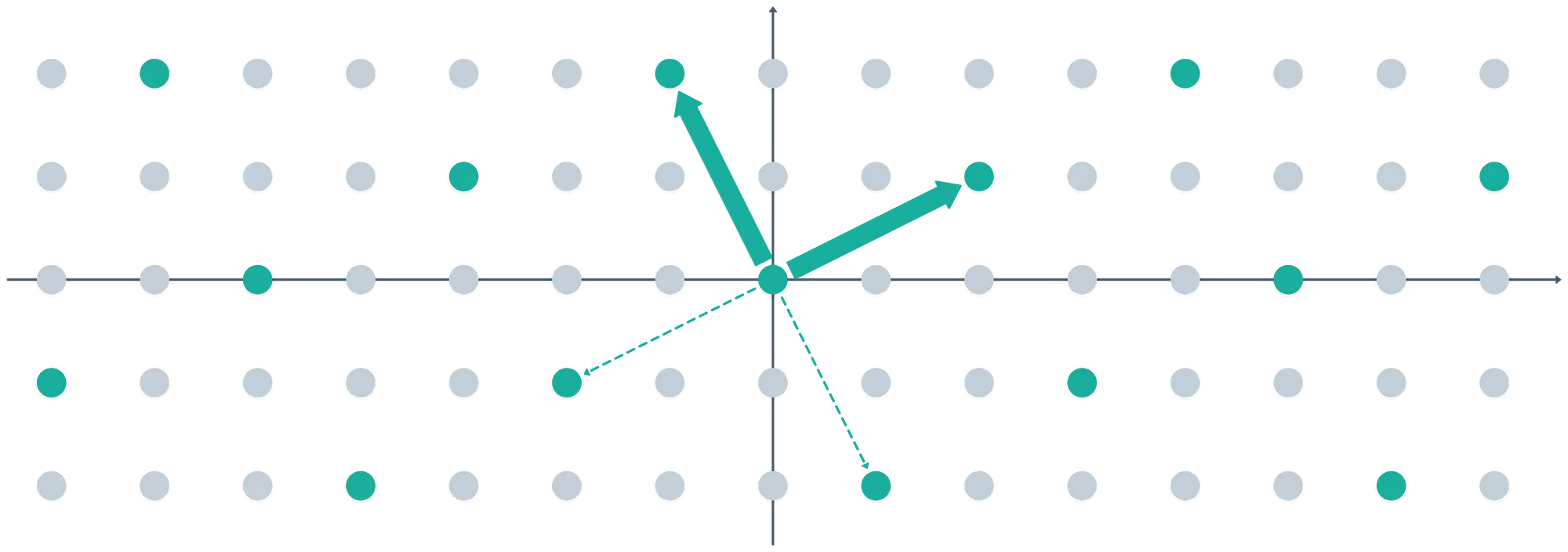
La elección de la base oculta un detalle sutil interesante. El segundo elemento se calculó como $x(x+ 2) = x^2 + 2x$. ¡Pero en el anillo que estamos usando, $x^2$ es equivalente a $-1$!

Multiplicar por $x$ tiene la agradable propiedad de rotar vectores en el anillo. ¡Por eso obtuvimos un buen par de vectores ortogonales!

Cada punto en la imagen (tanto los grises claros como los oscuros) es un elemento en el anillo $\mathbb{Z}[X]/(X^2+1)$. Y es fácil ver el ideal en acción aquí: no todos los puntos en el anillo están incluidos en el retículo del ideal.

Para entender mejor los cosets, simplemente toma un punto inicial diferente, y usa los mismos vectores base para generar un retículo:

Click to zoom

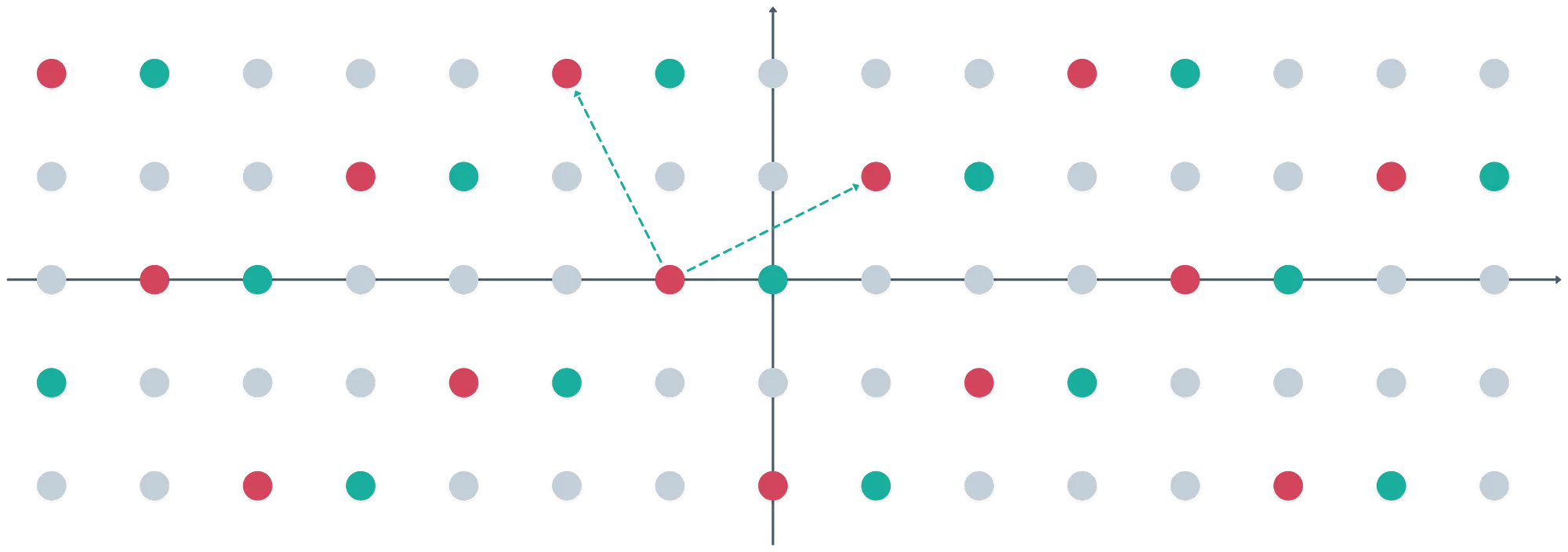
¿Ves lo que acaba de suceder? Obtenemos esencialmente el mismo patrón, pero desplazado. Estos son los cosets de los que hablamos. Interesantemente, cada coset puede identificarse por un solo elemento en él — luego, todos los demás elementos se generan sumando combinaciones lineales de los vectores base.

De hecho, el anillo cociente $R/I$ está formado por estos cosets distintos. Es solo que un único representante es suficiente para identificar el coset completo, que también es una clase de equivalencia.

Finalmente... ¿Qué significa tomar $\textrm{mod} \ B_i$? Es bastante simple, en realidad: cualquier vector en nuestro anillo $R$ puede representarse como la suma de combinaciones lineales de los vectores base, más un vector corto extra que nos permite movernos "lejos" del ideal:

Click to zoom

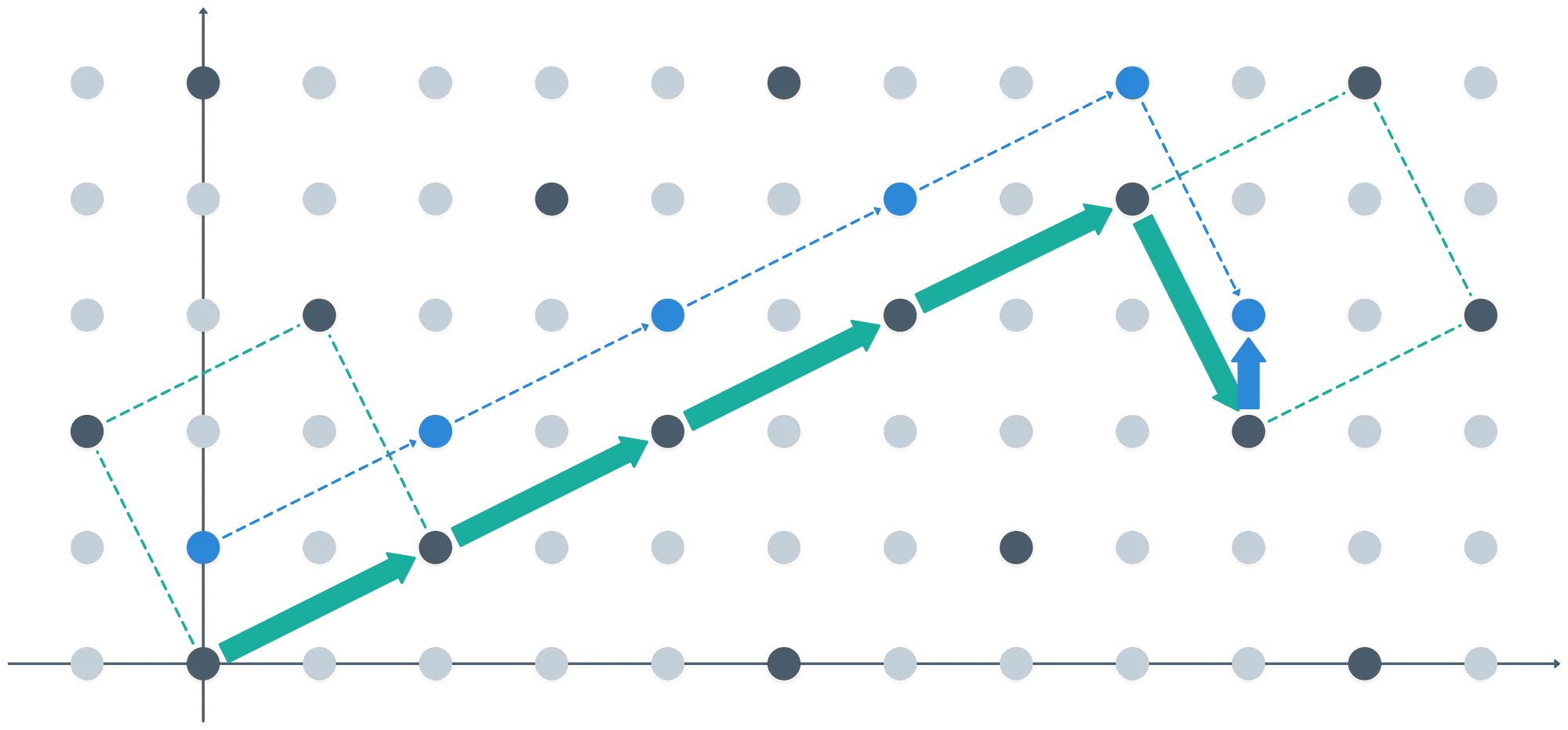
Podemos pensar en el vector azul como un residuo, siendo así el resultado de tomar $\textrm{mod} \ B_i$ en cualquier punto del anillo. ¡Pero también es un representante para un coset!

Formalmente, lo que sucede es que tomar $\textrm{mod} \ B_i$ en cualquier punto del anillo $R$, lo mapea a la clase de equivalencia respectiva en $R/I$. Por lo tanto, estos dos son equivalentes:

$$R / I = R \ \textrm{mod} \ B_I$$

Y los representantes para los cosets suelen ser elementos del paralelepípedo fundamental determinado por la base, que está resaltado por las líneas verdes punteadas en la imagen de arriba.

Esto no debería ser tan desconocido — es esencialmente la misma situación que describimos para el anillo de enteros módulo $q$:

$$\mathbb{Z}/(q) = \mathbb{Z}_q = \mathbb{Z} \ \textrm{mod} \ q$$

Y para cimentar esta idea, mira lo que sucede cuando pintamos todos los cosets en el ejemplo anterior:

Click to zoom

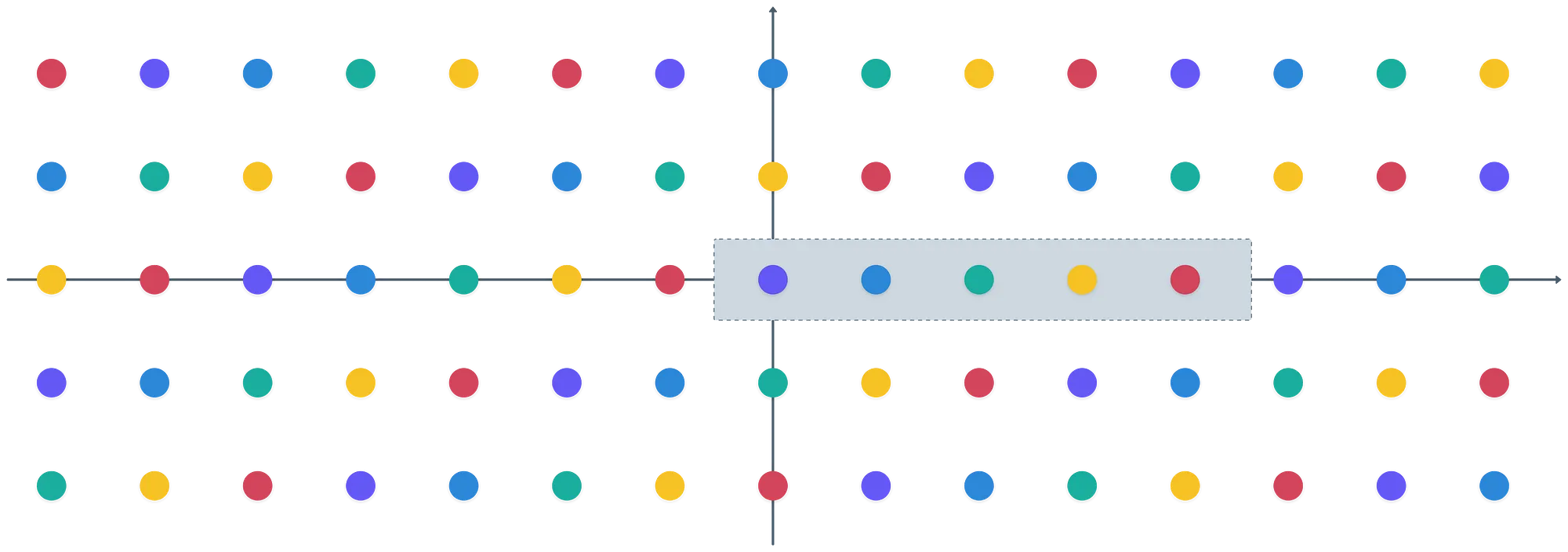
Cada elemento en $\mathbb{Z} \ \textrm{mod} \ q$ resulta mapear a un coset diferente en $R/I$, como podemos ver en el cuadro gris — y $q = 5$, que es el número de cosets distintos.

¡Genial! ¿Cómo nos sentimos hasta ahora?

La buena noticia es que después de que estos conceptos se entienden, ¡al menos podemos interpretar los procesos de encriptación y desencriptación!

Volvamos a enfocarnos en la función de encriptación:

$$\psi = (m + i) \ \textrm{mod} \ {B_J}^{pk}$$

Ahora estamos en condiciones de interpretar algunas cosas:

• $m$ representa un coset en $R/I$.
• $m + i$ es solo otro representante para el mismo coset. Podemos ver claramente cómo el espacio de texto plano está destinado a ser $R/I$.
• Sin embargo, tomar $\textrm{mod} \ B_j$ cambia las cosas un poco: el resultado será un representante de coset de $R/J$.

¿Aún no hemos hablado de $J$, verdad?

El ideal $J$ es diferente de $I$, de tal manera que usar cualquier base para $J$ en combinación con una base para I nos permite obtener cualquier elemento en el anillo $R$. Esto a veces se expresa como $I + J = R$, y decimos que $I$ y $J$ son coprimos.

Debido a esto, $i$ (que es solo una combinación lineal de los elementos base de $I$) esencialmente agrega algo de ruido a $m$. Lo que quiero decir es que estas dos expresiones generalmente no producen el mismo resultado:

$$m \ \textrm{mod} \ {B_J}^{pk} \neq (m + i) \ \textrm{mod} \ {B_J}^{pk}$$

Veremos esto en acción más adelante.

Desencriptación

Desencriptar el texto cifrado $\psi$ es tan simple como tomar un par de operaciones módulo:

$$m = (\psi \ \textrm{mod} \ {B_J}^{sk}) \ \textrm{mod} \ B_I$$

Lo que no es tan simple es entender por qué. Enfocémonos en el escenario más simple por un momento:

$$\psi = m \ \textrm{mod} \ {B_J}^{pk}$$

Entonces, sin ruido agregado.

También, asumamos por un momento que ambas bases para $J$ son iguales, y veamos qué sucede con un ejemplo, de nuevo.

$$I = (5 + 2x) \Rightarrow B_I = \{(5,2), (-2,5)\}$$ $$J = (7 + 3x) \Rightarrow B_J = \{(7,3), (-3,7)\}$$

Toma un mensaje $m$ dentro del paralelepípedo fundamental de $I$ (la forma definida por los vectores base):

Click to zoom

Como m está dentro del paralelepípedo fundamental de tanto $I$ como $J$, entonces tomar módulo durante la encriptación y desencriptación seguramente devolverá $m$. ¿Qué sucede si $J$ es "más fino", sin embargo?

Click to zoom

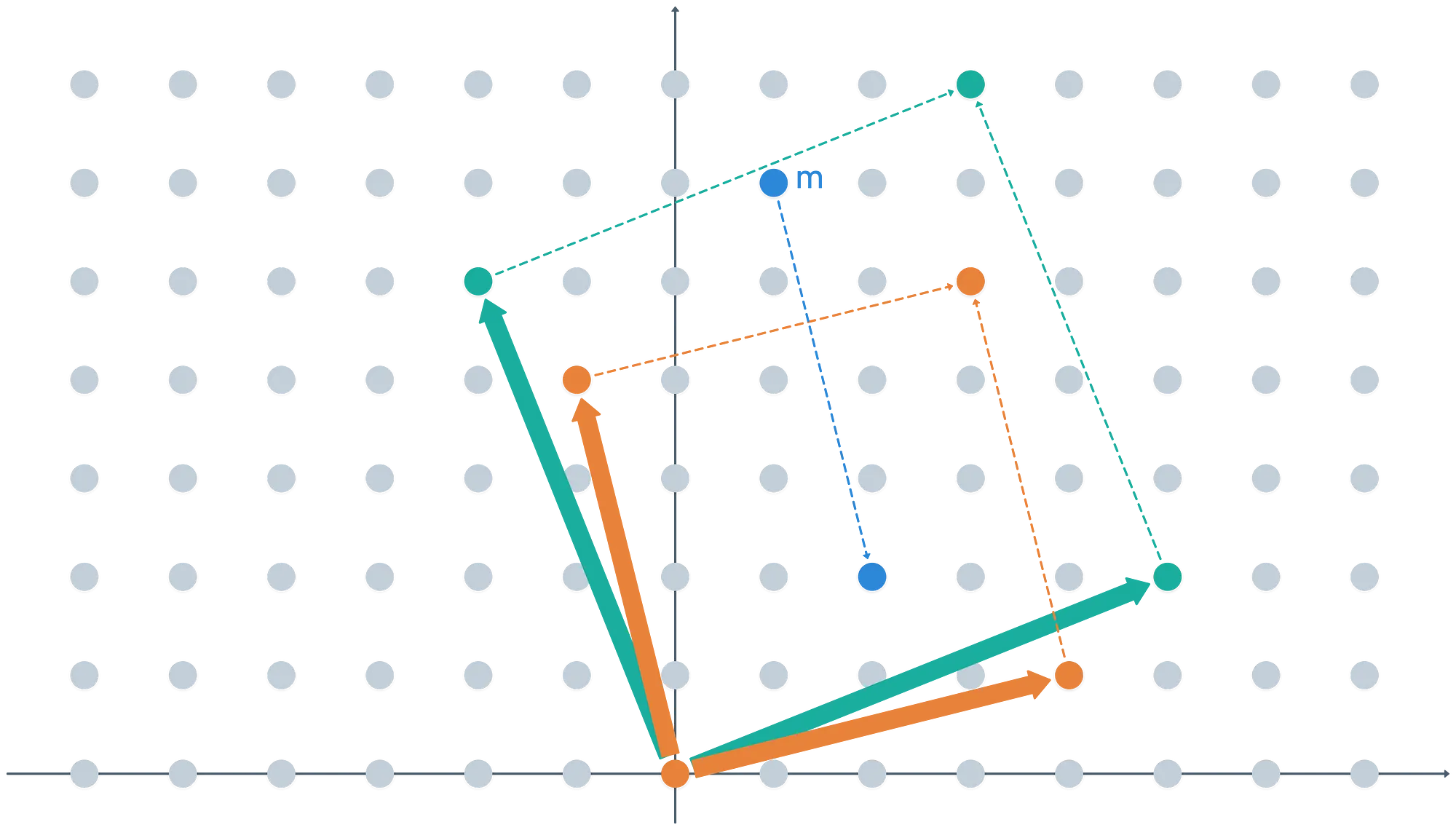
Nota que tomar la primera operación módulo mapea el mensaje a un nuevo coset de $R/I$ — ¡lo cual es algo que no queremos! Si esto sucede, obtendríamos un mensaje diferente al desencriptar. En este sentido, requerimos que $J$ sea algo así como más grueso que $I$.

Ahora, agreguemos algo de ruido $i$ al mensaje original, y usemos nuestro $J$ original. ¿Qué sucede en este caso si seguimos un ciclo completo de encriptación / desencriptación?

Click to zoom

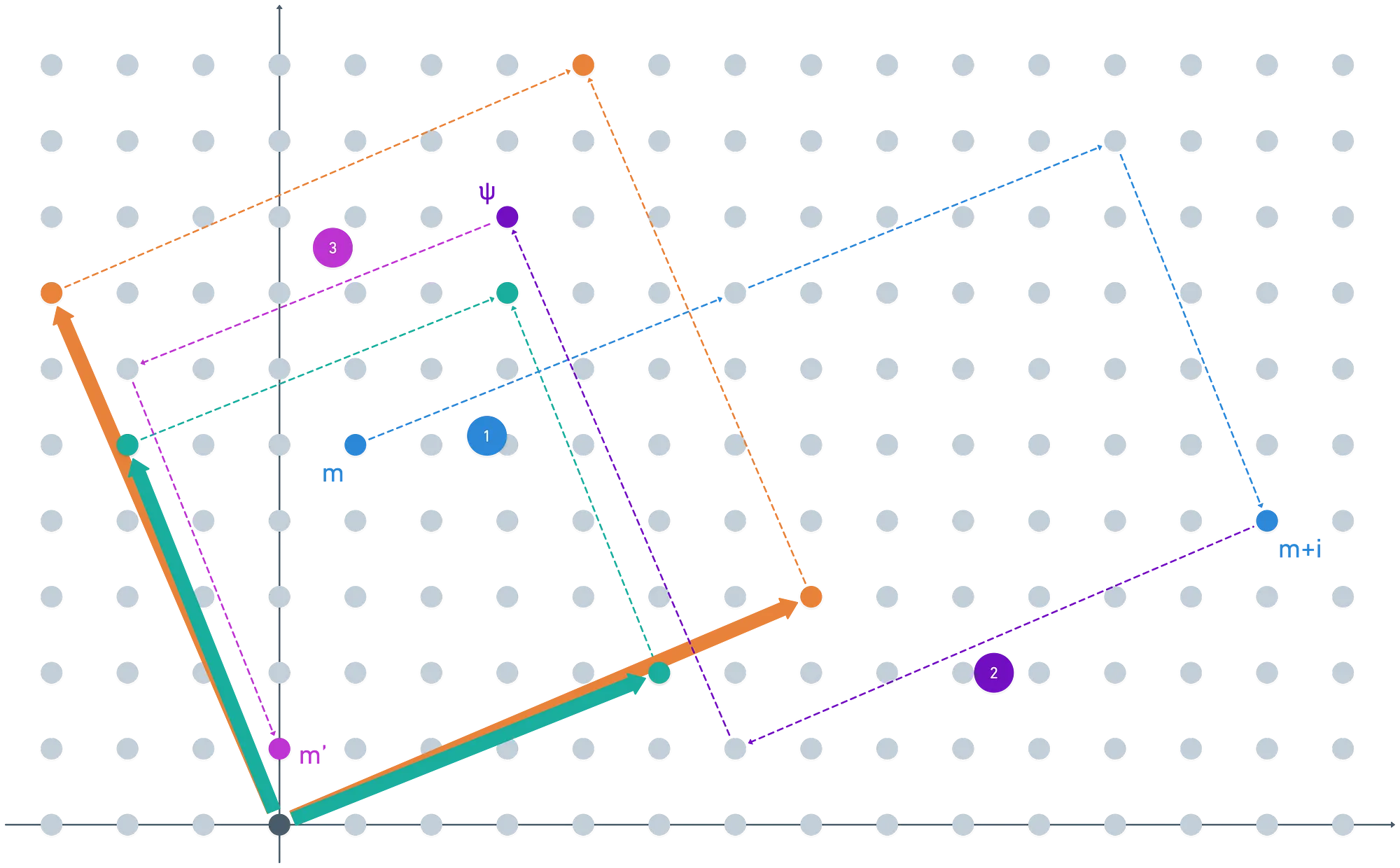
Como puedes ver... No recuperamos el texto plano original.

¿Qué está mal aquí?

En realidad, lo que acabamos de presenciar está en el núcleo de todo el asunto completamente homomórfico: nuestro error era demasiado grande. Si lo mantenemos un poco más pequeño, las cosas funcionarán bien:

Click to zoom

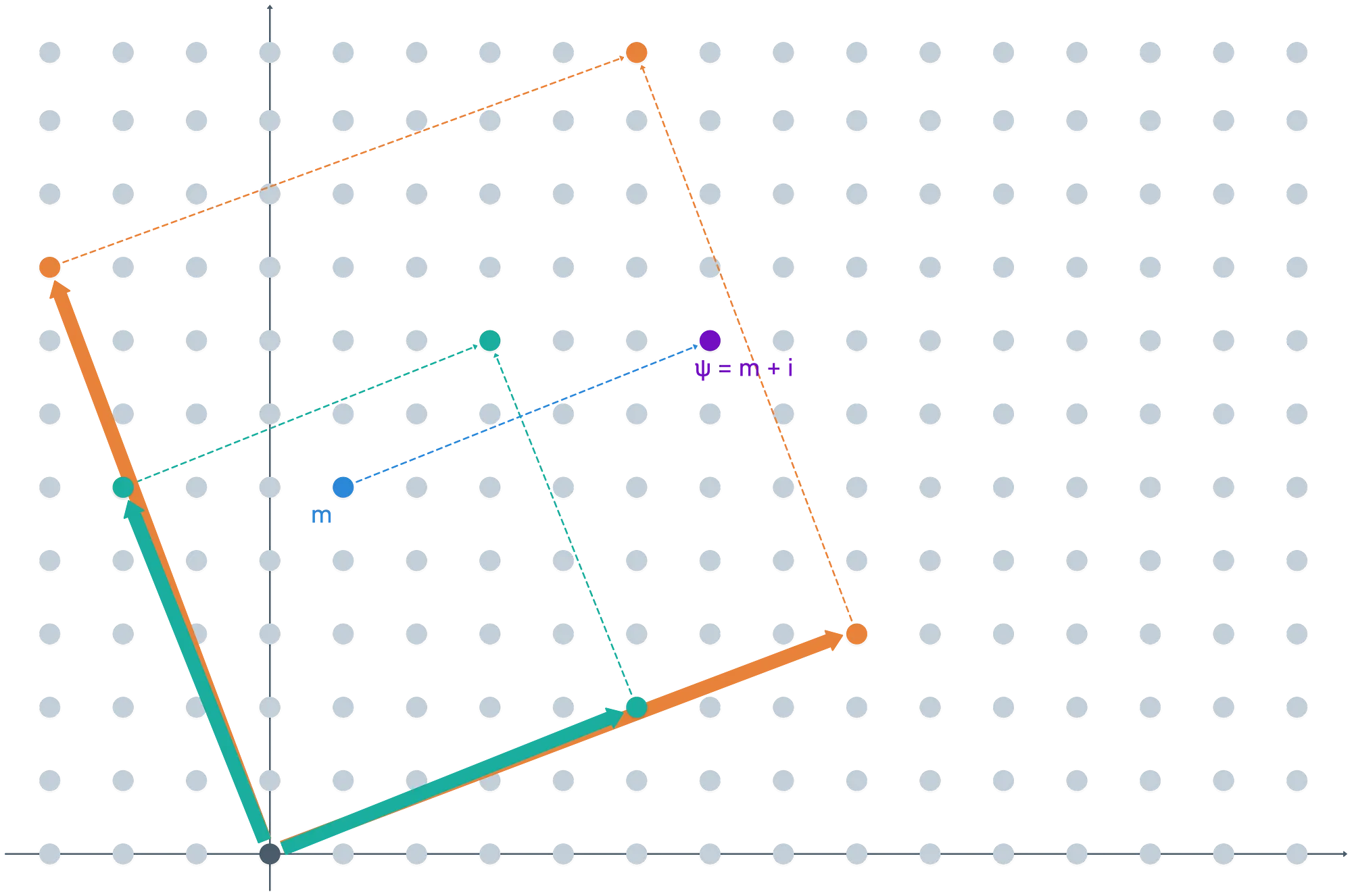
Durante la encriptación, lo más probable es que obtengamos un elemento en el coset de $J$ representado por $\psi$. Realmente no nos importa que esté dentro del paralelepípedo fundamental, solo que el valor represente el mismo coset. ¡Y eso también está estrechamente relacionado con por qué usamos dos bases!

Genial, eso lo resuelve: mientras el ruido sea pequeño, podemos desencriptar, sin problema. Pero recuerda, este artículo no es solo sobre encriptación — es sobre encriptación completamente homomórfica. ¿Qué sucede cuando comenzamos a realizar algunas operaciones?

Operaciones Homomórficas

Para que el esquema sea completamente homomórfico, debemos poder soportar tanto la suma como la multiplicación. Se comportan más o menos así:

$$\psi_1 + \psi_2 = (m_1 + m_2 + i_1 + i_2) \ \textrm{mod} \ {B_J}^{pk}$$ $$\psi_1.\psi_2 = (m_1.m_2 + m_1.i_2 + m_2.i_1 + i_1.i_2) \ \textrm{mod} \ {B_J}^{pk}$$

El ruido total durante la suma parece crecer de manera manejable, pero la multiplicación explota el ruido realmente rápido. Y esto complica las cosas: significa que después de algunas multiplicaciones, los errores pueden crecer hasta un punto donde la desencriptación ya no es posible. Como está, este es un esquema de Encriptación Algo Homomórfica — puede manejar una cantidad máxima de operaciones.

¡Aún es "mejor" que la mayoría de los otros esfuerzos previos a esta técnica, en el sentido de que teóricamente puede manejar más de una multiplicación!

Como si las cosas no fueran lo suficientemente complicadas... Oh, vaya.

¡Aguanta!

Manejo de Errores

Al realizar operaciones, los errores van a crecer sin importar qué. Es un parámetro que parece estar fuera de nuestro control — una propiedad intrínseca del esquema, por así decirlo.

Pero hay algo que podemos hacer para mantenerlos bajo control. Esta es la idea detrás de la tesis de Gentry: un esquema que permite refrescar los errores que son casi demasiado grandes, y obtener un error que es "más corto".

Obviamente, el error podría reducirse si se nos permitiera desencriptar el mensaje — solo necesitas elegir un nuevo vector de ruido pequeño. Pero por supuesto, el quid de la cuestión es hacer esto sin desencriptar. Ahí es donde las cosas se ponen interesantes. En las propias palabras de Gentry:

"¡desencriptamos el texto cifrado, pero homomórficamente!"

¡Lo sé, suena loco! Para dar una idea aproximada de lo que esto significa, llamemos a la función de encriptación $\mathcal{E}$ y a la función de desencriptación $\mathcal{D}$. Al desencriptar el texto cifrado, por supuesto esperamos recuperar el mensaje original:

$$m = \mathcal{D}(\psi, sk)$$

Si aplicamos la función de encriptación en ambos lados:

$$\mathcal{E}(m) = \mathcal{E}(\mathcal{D}(\psi, sk))$$

Esto es similar a desencriptar y encriptar de nuevo — a menos que de alguna manera tenga sentido evaluar $\mathcal{D}$ con una clave secreta encriptada, y obtener un nuevo texto cifrado refrescado.

¿Cómo podemos lograr esto?

Travesuras de Desencriptación

La idea clave aquí es pensar en el proceso de desencriptación como la evaluación de un circuito, similar a los que estudiamos unos artículos atrás. Es solo una serie de operaciones simples que resultan en el texto plano original (módulo $I$).

Con esto, podemos aprovechar el hecho de que nuestro esquema permite que se realicen algunas operaciones en el texto cifrado (es algo homomórfico). ¡Solo que, en lugar de usar la clave secreta real, usamos una encriptación de ella!

Es como resolver un rompecabezas dentro de una caja sellada. Más o menos.

Este proceso se llama bootstrapping. La mejor manera de convencerte de que todas estas travesuras funcionan es a través de un ejemplo simplificado. ¡Volvamos al tablero de dibujo!

Sea:

$$I = (4 + x) \Rightarrow B_I = \{(4,1), (-1,4)\}$$ $$J = (9 + 3x) \Rightarrow {B_J}^{sk} = \{(9,3), (-3,9)\}$$

Y también elegiremos una base mala ahora, como una combinación lineal de los vectores de la clave secreta:

$${B_J}^{pk} = \{(21,-3), (6,12)\}$$

Visualmente:

Click to zoom

Primero encriptemos un par de mensajes.

Supongamos $m_1 = (1,1)$, $m_2 = (0,2)$. Por supuesto, cuando se suman, estos deberían dar $(1,3)$. Esperamos que nuestro esquema devuelva este valor al desencriptar.

Después de agregar algo de ruido pequeño, obtenemos nuestros textos cifrados, que resultan en los vectores $\psi_1 = (5,2)$ y $\psi_2 = (4,3)$. Deberíamos poder sumarlos, y el resultado debería desencriptar a $m_1 + m_2$.

Click to zoom

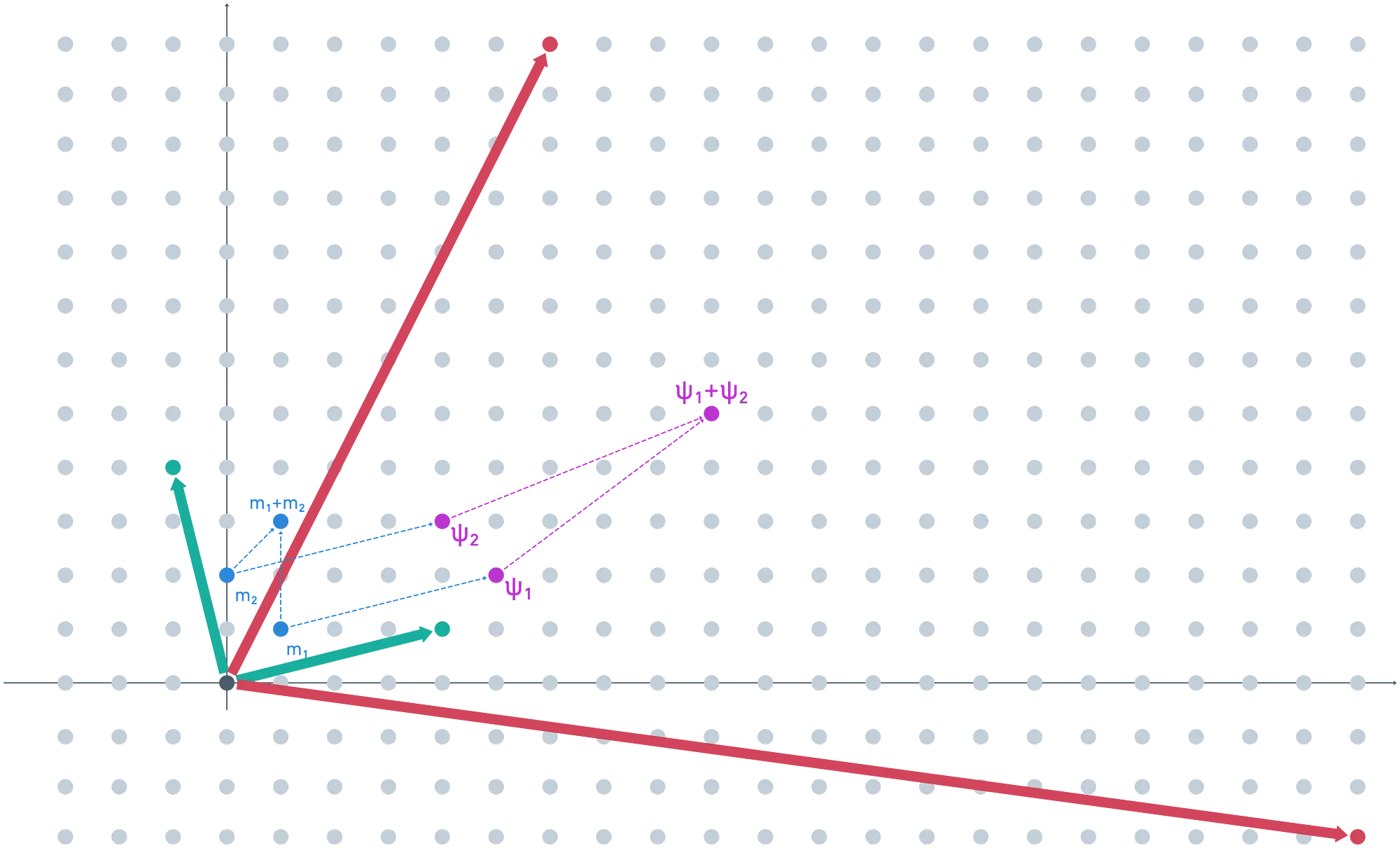
Ahora viene la parte divertida. Necesitamos encriptar la clave secreta, así que agregamos algo de ruido $i$ a cada vector (no tiene que ser el mismo valor que antes), y mapeamos los resultados módulo la clave pública. Obtenemos $k_1 = (10, -1)$ y $k_2 = (6,7)$ como los valores encriptados para la clave secreta.

Por simplicidad, elegí ruidos apropiados para que los resultados ya fueran parte del paralelepípedo fundamental de la clave pública.

Click to zoom

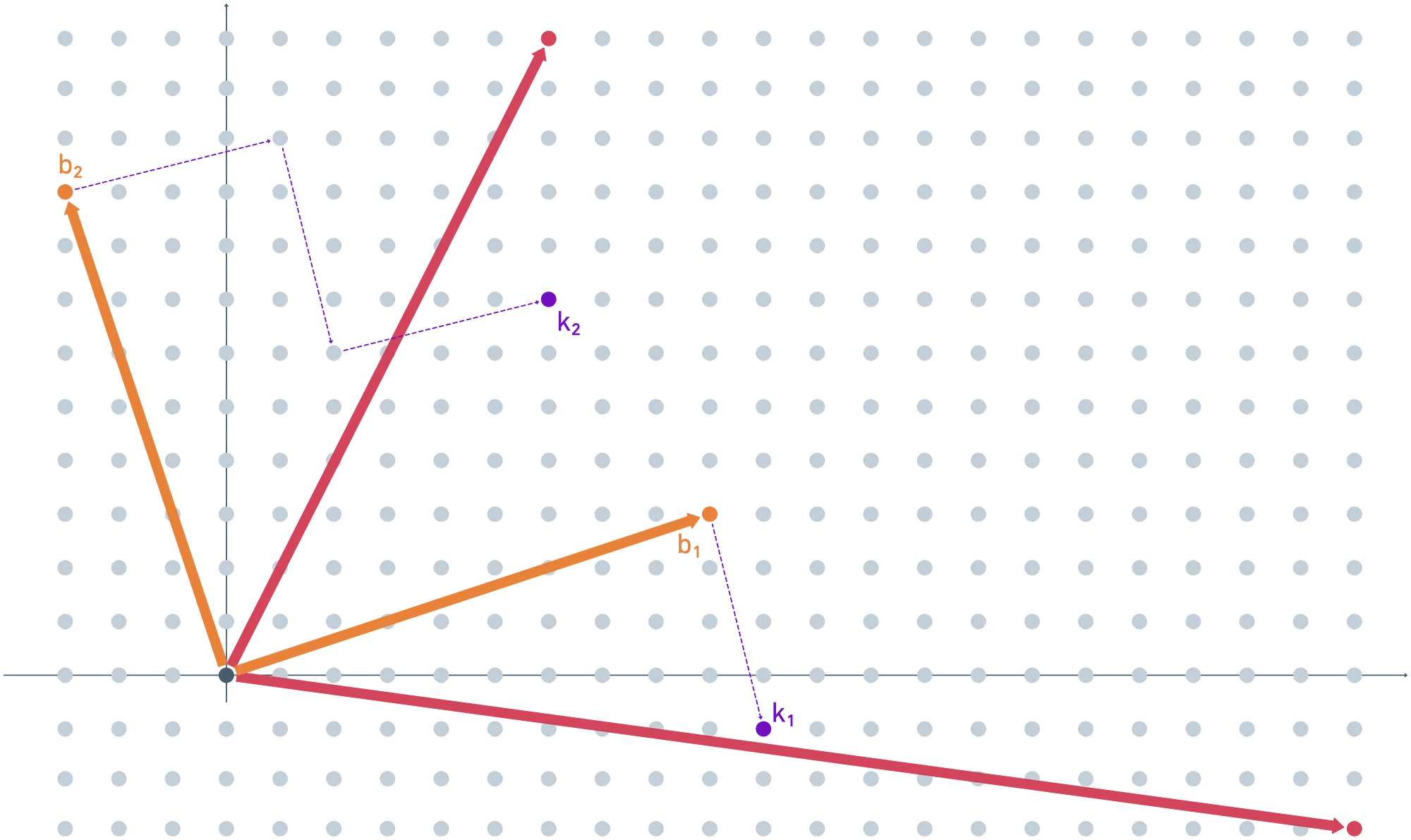
A continuación, queremos realizar esta cosa de desencriptación homomórfica. La idea es mapear el texto cifrado al dominio de la clave secreta, pero encriptado. Hacer esto produce $(12,1)$ — ¡nuestro texto cifrado refrescado!

Click to zoom

Todo lo que queda es verificar que esto se desencripta al valor correcto. Lo hacemos como antes — tomamos $\textrm{mod}$ la clave secreta (no encriptada), y luego mod nuestro dominio de texto plano, $I$.

Click to zoom

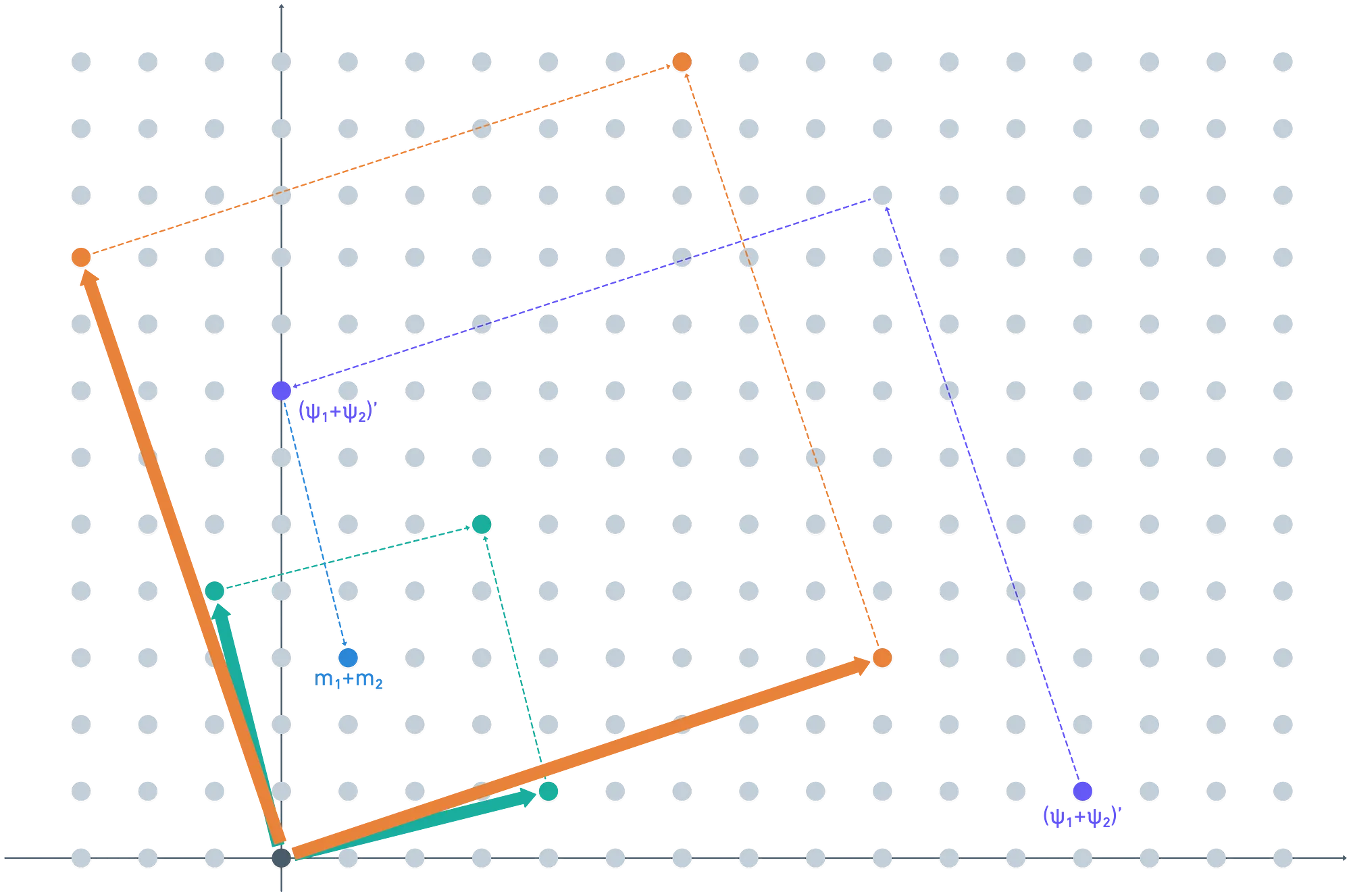
¡Justo como un reloj, recuperamos el valor correcto $(1,3)$!

Pero ¿qué pasó con los ruidos durante todo este asunto?

El ruido en este contexto se expresa como la combinación lineal más pequeña de vectores $B_I$ que resulta en un punto en el mismo coset (en $J$) que nuestro texto cifrado. Para el texto cifrado refrescado, es fácil ver que la diferencia es bastante pequeña (un solo vector en nuestra base).

Encontrar el representante para el $\psi_1 + \psi_2$ original no es tan simple, sin embargo. Aquí, te mostraré dónde coinciden los cosets:

Click to zoom

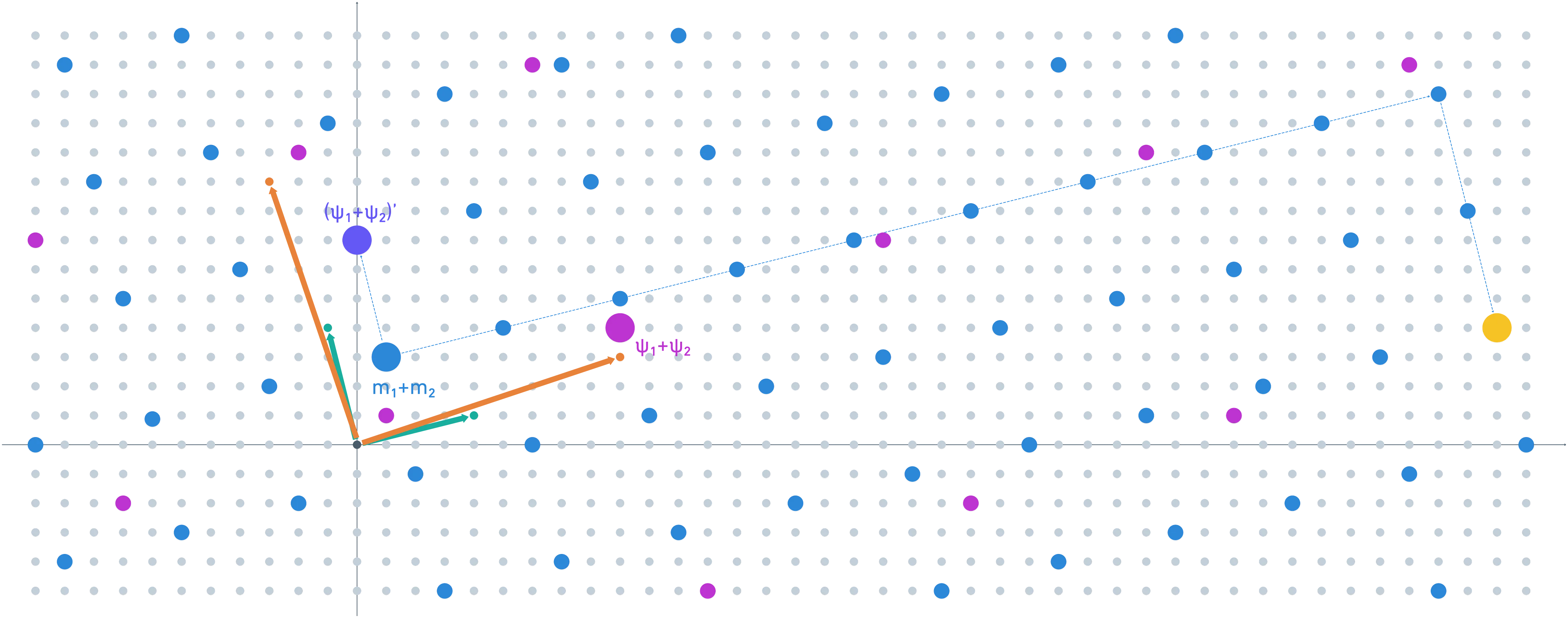
Admitidamente, este crecimiento del error se relaciona con una mala elección inicial de $J$.

En la construcción de Gentry, los vectores en la clave secreta ($R/J$) son decenas o cientos de veces más grandes que los vectores base para $R/I$. Nuestro escenario no cumple del todo con estos términos — ¡porque no podría posiblemente encajar todos esos puntos en una sola pantalla!

Pero bueno, al menos ayuda a ilustrar cómo funciona el proceso de bootstrapping. ¡Una porción bastante grande del ruido se redujo muy efectivamente!

Resumen

Por supuesto, la historia no termina aquí. Como está, este algoritmo es muy impráctico. El artículo original (y la tesis, que es un poco más amigable de leer) en realidad introduce algunas mejoras para que el algoritmo sea práctico, pero no entraremos en eso.

Lo importante es que este trabajo probó que FHE era posible. El código había sido descifrado, y algo que parecía inalcanzable se hizo posible.

Hoy en día, hay técnicas más nuevas y brillantes que mejoran el trabajo original de Gentry (después de todo, fue publicado hace 15 años). Por ejemplo, está este artículo de 2011 donde se propone otro método para FHE sin bootstrapping. O este artículo de 2014, que describe un método FHE mucho más rápido.

¡Spoiler: no se pone más fácil que este artículo aquí!

El campo ha evolucionado bastante, así que me gustaría que pienses en este texto como una breve introducción al tema.

¡Y si necesitas FHE implementado en un proyecto, hay muchas bibliotecas por ahí para este propósito.

Palabras de Cierre

¡Qué viaje ha sido!

Aunque he aprendido mucho durante la realización de esta serie, diré exactamente lo mismo que dije al principio: todavía no soy un experto en el tema — solo un tipo tratando de aprender el oficio por su cuenta.

¡Y que tal vez es un poco más conocedor!

Aún así, creo que este viaje fue profundamente enriquecedor.

La enorme cantidad de información y herramientas disponibles hoy en día es simplemente asombrosa. Es más fácil que nunca aprender cosas.

Pero a veces, es difícil no caer en agujeros de conejo sin fin, o no enredarse en las malezas — especialmente cuando se trata de temas altamente especializados. Mi objetivo era simplificar un poco, y hacer las cosas un poco más digeribles.

Espero sinceramente que esta serie haya dado en el clavo al ayudar a alguien a entender mejor los conceptos muy complejos que la criptografía tiene para ofrecer. Y espero que te hayas reído una o dos veces en el camino. Para mí al menos, ha sido súper divertido.

¡Espero verte pronto! ¡Y mantente atento para más contenido!