Criptografía 101: Emparejamientos

Este artículo forma parte de una serie más larga sobre criptografía. Si este es el primer artículo con el que te encuentras, te recomiendo encarecidamente comenzar desde el principio de la serie.

Ya hemos explorado varias aplicaciones para las curvas elípticas — algunos esquemas simples y otros más avanzados. También incorporamos polinomios cuando estudiamos las firmas de umbral. Si forzamos los límites de la creatividad, aún podemos idear muchos protocolos basados únicamente en estas construcciones.

Pero esto no significa que no existan otras herramientas por ahí. Y hay una muy importante que aún necesitamos presentar: los emparejamientos.

En este artículo, definiremos qué son — pero no cómo calcularlos. La razón es que aún no hemos definido la maquinaria matemática necesaria para el cálculo de emparejamientos. Esto lo exploraremos quizás más adelante, pero si estás interesado, este es un excelente recurso para consultar mientras tanto. ¡Y también hay muchas bibliotecas disponibles que cubren el cálculo de emparejamientos si quieres comenzar a experimentar con ellos después de leer este artículo!

Emparejamientos

Un emparejamiento (pairing), también conocido como una mapa bilineal, es realmente solo una función, típicamente representada con la letra $e$. Toma dos argumentos y produce una única salida, así:

$$e: \mathbb{G}_1 \times \mathbb{G}_2 \rightarrow \mathbb{G}_3 \ / \ e(G_1, G_2) = G_3$$

Necesitaremos algo de notación de la teoría de conjuntos esta vez, pero nada demasiado complicado.

Probablemente la más exótica (si no has tenido mucho contacto previo con la teoría de conjuntos) es el producto cartesiano — usado en el conjunto $\mathbb{G}_1 \times \mathbb{G}_2$. Es simplemente el conjunto de todos los elementos de la forma $(G_1, G_2)$ donde $G_1$ pertenece a $\mathbb{G}_1$ y $G_2$ pertenece a $\mathbb{G}_2$.

Sin embargo, esta no es una función ordinaria. Tiene una propiedad importante: es lineal en ambas entradas. Esto significa que todas las siguientes expresiones son equivalentes:

$$e([a]G_1, [b]G_2) = e(G_1, [b]G_2)^a = e(G_1, G_2)^ab = e([b]G_1, [a]G_2)$$

Como puedes ver, podemos hacer este tipo de intercambio de los productos (o más precisamente, operaciones de grupo). Aunque esta propiedad no parece gran cosa a primera vista, es realmente muy poderosa.

Los emparejamientos son una especie de licuadora, en el sentido de que no nos importa tanto el valor particular obtenido al evaluar una expresión de emparejamiento (excepto cuando verificamos algo llamado no-degeneración). En su lugar, lo que nos importa es que algunas combinaciones de entradas producen el mismo resultado, debido a la bilinealidad que mencionamos anteriormente. Esto es lo que los hace atractivos, como veremos más adelante.

Curvas Elípticas y Emparejamientos

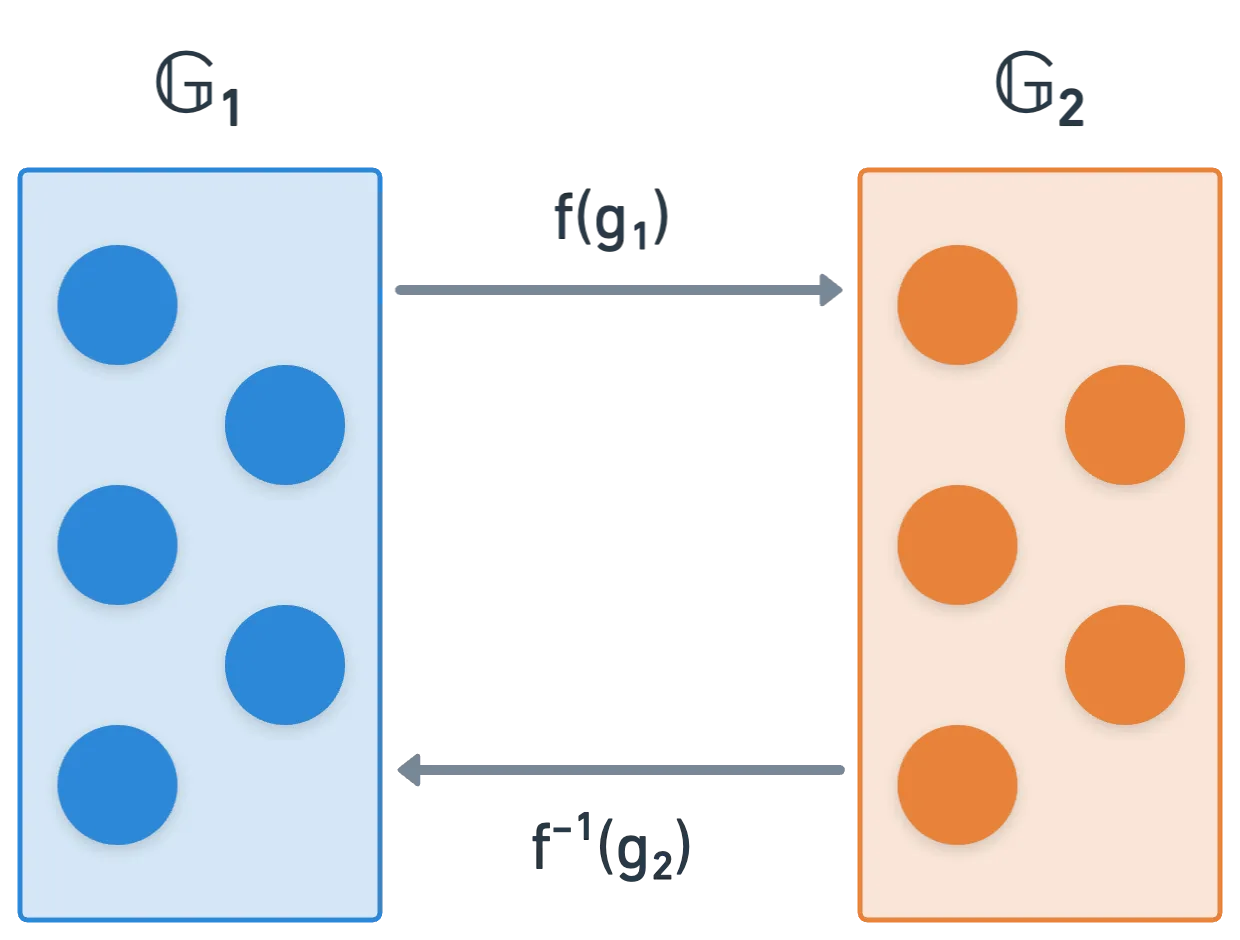
Podemos ver que las entradas provienen del producto cartesiano $\mathbb{G}_1 \times \mathbb{G}_2$. Es un conjunto bastante particular: $\mathbb{G}_1$ y $\mathbb{G}_2$ son grupos, para ser precisos. Grupos disjuntos, de hecho — lo que significa que no comparten ningún elemento. Formalmente, decimos que su intersección está vacía:

$$\mathbb{G}_1 \cap \mathbb{G}_2 = \varnothing$$

Además, $\mathbb{G}_1$ y $\mathbb{G}_2$ no son simplemente grupos cualquiera — deben ser adecuados para el cálculo de emparejamientos. Resulta que los grupos de curvas elípticas son una buena elección — y muy buena en términos de eficiencia computacional. ¡Así que es una feliz coincidencia que ya tengamos un buen dominio sobre ellos!

Si consultas la literatura, hay casos donde en lugar de usar dos grupos disjuntos, verás el mismo grupo usado dos veces. Algo como $\mathbb{G} \times \mathbb{G}$.

Estos a veces se llaman auto-emparejamientos, y lo que realmente sucede es que hay una función f que mapea $\mathbb{G}_2$ en $\mathbb{G}$ — lo que significa que podemos transformar elementos de $\mathbb{G}_2$ en elementos de $\mathbb{G}$, y simplemente usar $\mathbb{G}$ en nuestro emparejamiento.

Aunque no cubriremos cómo se hace esto, ten en cuenta que la definición formal de un emparejamiento requiere que los grupos sean disjuntos.

Click to zoom

Aplicación

Antes de llegar al punto de "¿por qué diablos estoy aprendiendo esto?" (¡asumiendo que aún no hemos llegado!), creo que es fructífero presentar una aplicación.

A pesar de que aún no sabemos cómo calcular emparejamientos, podemos entender su utilidad porque conocemos sus propiedades.

No perdamos tiempo y vayamos directo al grano.

La Configuración

Trabajar con grupos de curvas elípticas, o incluso con enteros módulo $p$, puede llevarte muy lejos. Pero ¿sabes algo que ninguno de ellos puede hacer por ti? ¡No te permiten usar tu identidad para operaciones criptográficas!

¿Identidad? ¿Te refieres a algo como mi nombre? Suena descabellado, pero se puede hacer. Aunque se requiere cierta configuración.

Para realizar esta hazaña de magia criptográfica, necesitaremos un actor especial, en quien confían otras partes — a menudo referido como una Autoridad de Confianza. Este actor estará a cargo de la generación de claves privadas, por lo que también se denomina de manera precisa (y muy descriptiva) Generador de Claves Privadas (PKG).

El PKG hace algunas cosas. En primer lugar y más importante, elige un secreto maestro, que es un entero $s$. También elige y hace públicos algunos parámetros públicos, que definiremos en un momento. Y finalmente, elige y hace pública una función de hash $H$, que devuelve valores en $\mathbb{G}_1$.

$$H: \{0,1\}^* \rightarrow \mathbb{G}_1$$

Para obtener una clave privada, Alicia debe solicitarla al PKG. Y para hacerlo, le envía su identidad hasheada. Su identidad podría ser cualquier cosa — un nombre, una dirección de correo electrónico, un número de documento de identidad, cualquier cosa que identifique de manera única a un individuo. Denotaremos esto como $ID$. Su clave pública es entonces:

$$Q_A = H(ID_A) \in \mathbb{G}_1$$

Al recibir este valor, el PKG calcula su clave privada como:

$$S_A = [s]Q_A \in \mathbb{G}_1$$

Y se la envía a Alicia.

Se asume que todas estas comunicaciones ocurren a través de un canal seguro. ¡En particular, la clave secreta de Alicia no debe filtrarse!

Click to zoom

¡Nuestra configuración está completa! Alicia tiene tanto su clave privada como pública. ¿Qué puede hacer con esto?

Encriptación Basada en Identidad

Supongamos que Alicia quiere cifrar un mensaje para Bruno. Todo lo que tiene es su clave pública, porque conoce su identidad ($ID$). Y simplemente hasheándola, obtiene su clave pública:

$$Q_B = H(ID_B)$$

También vamos a necesitar un par de cosas más:

• Un punto $P \in \mathbb{G}_2$, usado para calcular un punto $Q = [s]P$, también en $\mathbb{G}_2$. Como $s$ solo es conocido por la autoridad de confianza, estos puntos son calculados y publicados por el PKG — son los parámetros públicos que mencionamos anteriormente, y los denotaremos por $p$:

$$p = (P, Q)$$

• También necesitamos otra función hash $H'$:

$$H': \mathbb{G}_3 \rightarrow \{0,1\}^n$$

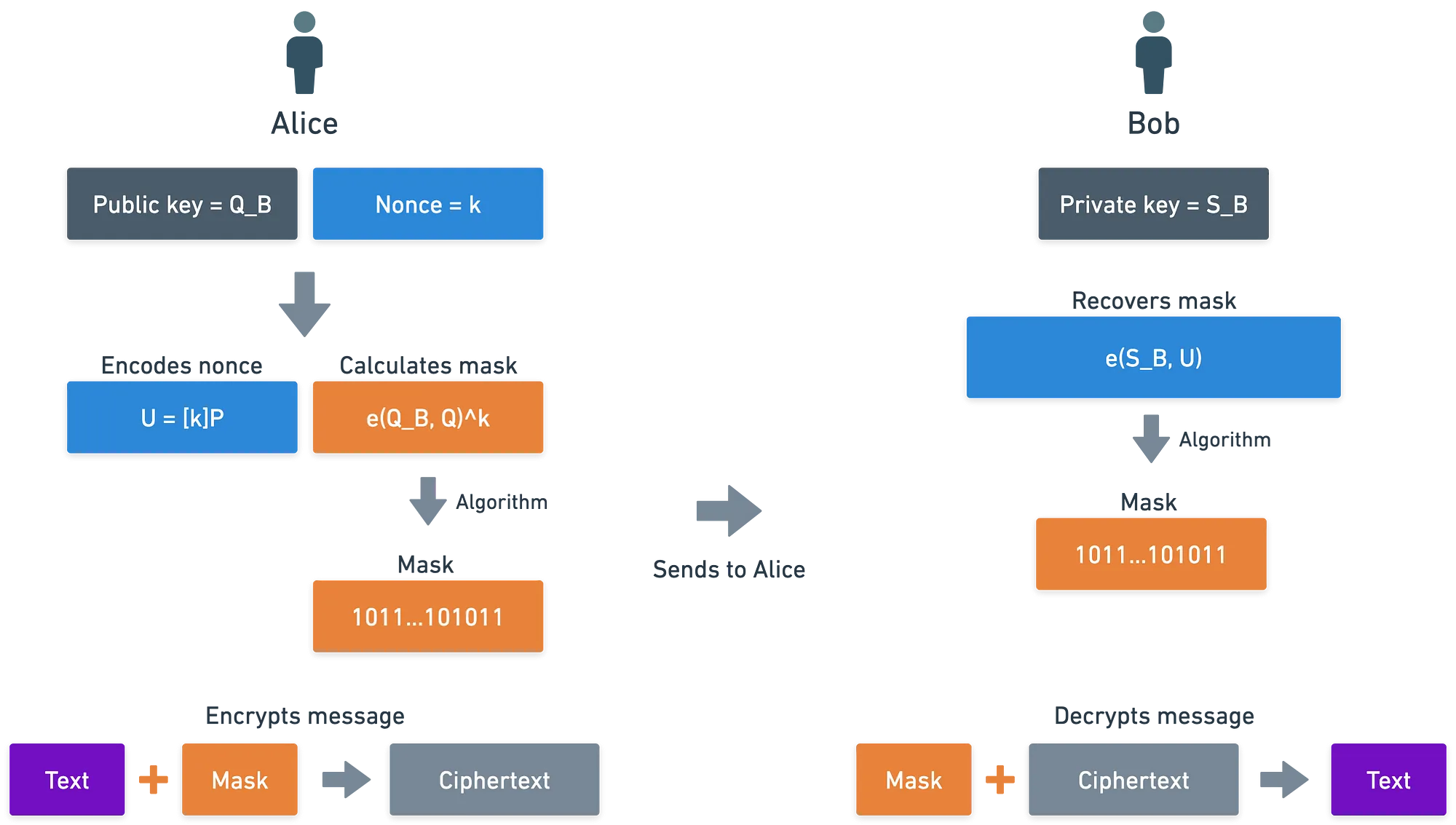
Este esquema de cifrado utiliza una estrategia similar al Esquema de Cifrado Integrado de Curvas Elípticas que vimos anteriormente en la serie: enmascaramiento. Así, para cifrar un mensaje $M$, Alicia sigue estos pasos:

• Elige un nonce aleatorio, que es un entero $k$.
• Con él, calcula $U = [k]P$. Esto se usará posteriormente para reconstruir la máscara.
• Luego, usando la clave pública de Bruno, que es simplemente el hash de su identidad, calcula:

$$e(Q_B,Q)^k$$

• Usa este valor para calcular una máscara, que se añade al mensaje:

$$V = M \oplus H'(e(Q_B,Q)^k)$$

El mensaje cifrado final será la tupla $(U, V)$.

Recuerda que el símbolo $\oplus$ representa la operación XOR. Y una de las propiedades de esta operación es: $M \oplus A \oplus A = M$. Lo que significa que añadir la máscara dos veces nos permite recuperar el mensaje original.

¿Cómo desencripta Bruno? Bueno, puede tomar $U$ y simplemente recalcular la máscara. Con ella, vuelve a obtener el mensaje original:

$$M = V \oplus H'(e(S_B,U))$$

Pero espera... ¿Cómo es que las dos máscaras son iguales? Claramente, no parecen lo mismo... ¡Son evaluaciones diferentes del emparejamiento!

$$e(Q_B,Q)^k \stackrel{?}{=} e(S_B,U)$$

No temas — prometo que esto tiene sentido. Porque es precisamente aquí donde ocurre la magia de los emparejamientos: usando su propiedad de bilinealidad, podemos demostrar que los dos valores son equivalentes:

$$e(Q_B,Q)^k = e(Q_B, [s]P)^k = e(Q_B, P)^{s.k} = e([s]Q_B, [k]P)$$ $$e(Q_B,Q)^k = e(S_B, U)$$

Y así, conocer solo la identidad de Bruno es suficiente para que Alicia cifre información solo para él — ¡con la ayuda de los emparejamientos, por supuesto!

Click to zoom

Volviendo a los Emparejamientos

Bien, ahora que hemos visto los emparejamientos en acción, estamos completamente motivados para entender cómo se definen con un poco más de profundidad. ¿Verdad? ¿VERDAD?

Esto no tomará mucho tiempo—solo echaremos un vistazo rápido a algunas de las ideas que hacen posibles los emparejamientos.

Mencionamos que $\mathbb{G}_1$ y $\mathbb{G}_2$ podrían ser perfectamente grupos de curvas elípticas.

Entonces, ¿simplemente elegimos dos curvas elípticas diferentes? Bueno, en ese caso, tendríamos que asegurarnos de que los grupos sean disjuntos, lo que no es necesariamente fácil; y hay otras preocupaciones en tal escenario.

¿Qué tal usar una sola curva elíptica? Entonces necesitaríamos dos subgrupos diferentes. Cuando utilizamos un generador de grupo, $G$, el grupo generado por él no es necesariamente la totalidad del grupo de curvas elípticas, aunque podría serlo. Esta relación de inclusión se escribe como:

$$\langle G \rangle \subseteq E(\mathbb{F}_q)$$

Lo que significa: el grupo generado por $G$ es un subgrupo, o la curva elíptica completa.

Normalmente queremos que el orden del subgrupo generado por $G$ sea lo más grande posible, para que el problema DLP sea difícil. Esto significa que:

• Si hay otros subgrupos, probablemente son pequeños.
• Si $\langle G \rangle$ es la totalidad de la curva elíptica, entonces no hay otros subgrupos disponibles.

Parece que hemos llegado a un dilema...

Expandiendo la Curva

Por suerte, esta pequeña crisis nuestra tiene solución. Verás, nuestras curvas siempre han estado definidas sobre los enteros módulo $q$ — pero ¿qué pasaría si pudiéramos extender los posibles valores que usamos?

En lugar de permitir que los puntos en la curva elíptica tomen valores solo en los enteros módulo $q$:

$$\mathbb{F}_q = \{0,1,2,3,..., q-1\}$$

Podríamos usar algo como los números complejos, y permitir que los puntos en $E$ tomen valores en este conjunto:

$$\mathbb{F}_{q^2} = \{a + bi : a, b \in \mathbb{F}_q, i^2 + 1 = 0 \}$$

Usar números complejos tiene perfecto sentido: por ejemplo, puedes comprobar por ti mismo que el punto $(8, i)$ se encuentra en la siguiente curva elíptica:

$$E/\mathbb{F}_{11}: y^2 = x^3 + 4$$

Extensiones de Cuerpo

Los números complejos son solo un ejemplo de un concepto más general, que son las extensiones de cuerpo.

Un cuerpo (o también llamado campo - lo denotaremos $F$) es simplemente un conjunto con algunas operaciones asociadas. Esto probablemente te suena familiar — es una definición muy similar a la que dimos para grupos, al principio de la serie.

Independientemente de la formalidad, hay un campo muy importante del que debemos preocuparnos: los enteros módulo $q$, cuando $q$ es un número primo.

Esto puede sonar un poco engañoso. Originalmente, te dije que los enteros módulo $q$ eran un grupo. Y de hecho, si usamos una sola operación (como la suma), se comportan como un grupo.

Más generalmente, sin embargo, son un cuerpo, ya que admiten suma, resta, multiplicación y división (bueno, realmente inversos modulares).

Una extensión de cuerpo es simplemente un conjunto $K$ que contiene el cuerpo original:

$$F \subset K$$

Bajo la condición de que el resultado de operaciones entre elementos de $F$ siempre se encuentre en $F$, pero nunca en el resto de $K$ (el conjunto $K - F$).

Un ejemplo muy conocido de extensión de cuerpo es, por supuesto, el conjunto de los números complejos. Los números reales actúan como $F$, y las operaciones entre números reales (suma, resta, multiplicación y división) también se encuentran en los números reales ($F$). Las operaciones entre números complejos pueden o no resultar en números reales.

¿Por qué importa esto? Imagina que definimos una curva sobre los enteros módulo $q$. Obtenemos un montón de puntos, que podemos denotar:

$$E(F)$$

Si extendemos el cuerpo base (los enteros módulo $q$), entonces aparecerán nuevos puntos válidos, mientras preservamos los antiguos. Esto es:

$$E(F) \subseteq E(K)$$

Debido a esto, aparecen nuevos subgrupos, y obtenemos la ventaja adicional de mantener los subgrupos originales, que fueron definidos sobre el cuerpo base.

Y cuando elegimos una extensión de cuerpo apropiada, sucede algo asombroso: obtenemos una plétora de subgrupos con el mismo orden que $\langle G \rangle$. Y estos grupos resultan ser casi disjuntos: solo comparten el elemento identidad, $\mathcal{O}$. El conjunto de todos estos subgrupos es lo que se llama el grupo de torsión.

Click to zoom

Bien, detengámonos ahí. El objetivo de esta sección es simplemente presentar una idea general de cuáles son las entradas de los emparejamientos. Sin embargo, no hay mucho más que podamos decir sin profundizar más en el tema, algo que excede el alcance de este artículo introductorio.

De nuevo, recomiendo este libro si quieres una explicación más detallada — y a su vez, hace referencia a algunos recursos más avanzados excelentes.

La idea importante aquí es que el cálculo de emparejamientos no es trivial, en absoluto. Si estás interesado en que amplíe este tema en próximos artículos, ¡házmelo saber!

Resumen

Aunque no nos hemos adentrado profundamente en el territorio de los emparejamientos, esta simple introducción nos permite entender el principio de funcionamiento detrás de los métodos basados en emparejamientos. Todo gira en torno a la propiedad de bilinealidad que vimos al principio del artículo.

La conclusión clave es:

Los emparejamientos son una especie de licuadoras, donde nos importa que el resultado calculado sea el mismo para dos conjuntos diferentes de entradas

De nuevo, podríamos profundizar en el cálculo de emparejamientos más adelante. Creo que es más fructífero comenzar a ver algunas aplicaciones en su lugar.

Por esta razón, veremos un par más de aplicaciones de emparejamientos en la próxima entrega de la serie. ¡Hasta entonces!