Criptografía 101: Protocolos a Montones

Este artículo forma parte de una serie más larga sobre criptografía. Si este es el primer artículo con el que te encuentras, te recomiendo comenzar desde el principio de la serie.

¡Muy bien! Ya hemos avanzado bastante. Tenemos grupos (y en particular curvas elípticas) y hashing como herramientas a nuestra disposición, y ya hemos visto cómo funcionan.

Pero se pueden hacer muchas más cosas con lo que ya sabemos. Este artículo estará dedicado a enumerar y explicar protocolos criptográficos basados en curvas elípticas.

Debo señalar que los mismos protocolos pueden construirse utilizando el grupo de enteros módulo $q$. Nos quedaremos con las curvas elípticas, ya que hay algunos beneficios en usarlas. Esa discusión ocurrirá en otro momento.

Esta lista no es en absoluto completa — hay muchas más protocolos por aprender. Aun así, esto debería proporcionar una base sólida para tener una buena comprensión de lo que es posible con lo que sabemos hasta ahora.

Prepárate, ¡vamos a sumergirnos directamente en esto!

Intercambio de Claves

¿Recuerdas el ejemplo de cifrado simétrico? Se basaba en el uso de una clave secreta compartida. Mencionamos brevemente que compartir una clave secreta a través de un canal inseguro no es una buena idea — cualquiera podría estar escuchando. Y si lo hacen, y obtienen la clave compartida, ¡entonces podrían descifrar cualquier mensaje posterior!

Afortunadamente, existen mecanismos para generar claves compartidas de manera segura. La técnica más común para hacer esto es el algoritmo de intercambio de claves Diffie-Hellman. Este método fue formulado originalmente utilizando los enteros módulo $q$, pero puede adaptarse fácilmente a curvas elípticas — y obtenemos el llamado método Diffie-Hellman de Curva Elíptica (ECDH). Así es como se ve:

Click to zoom

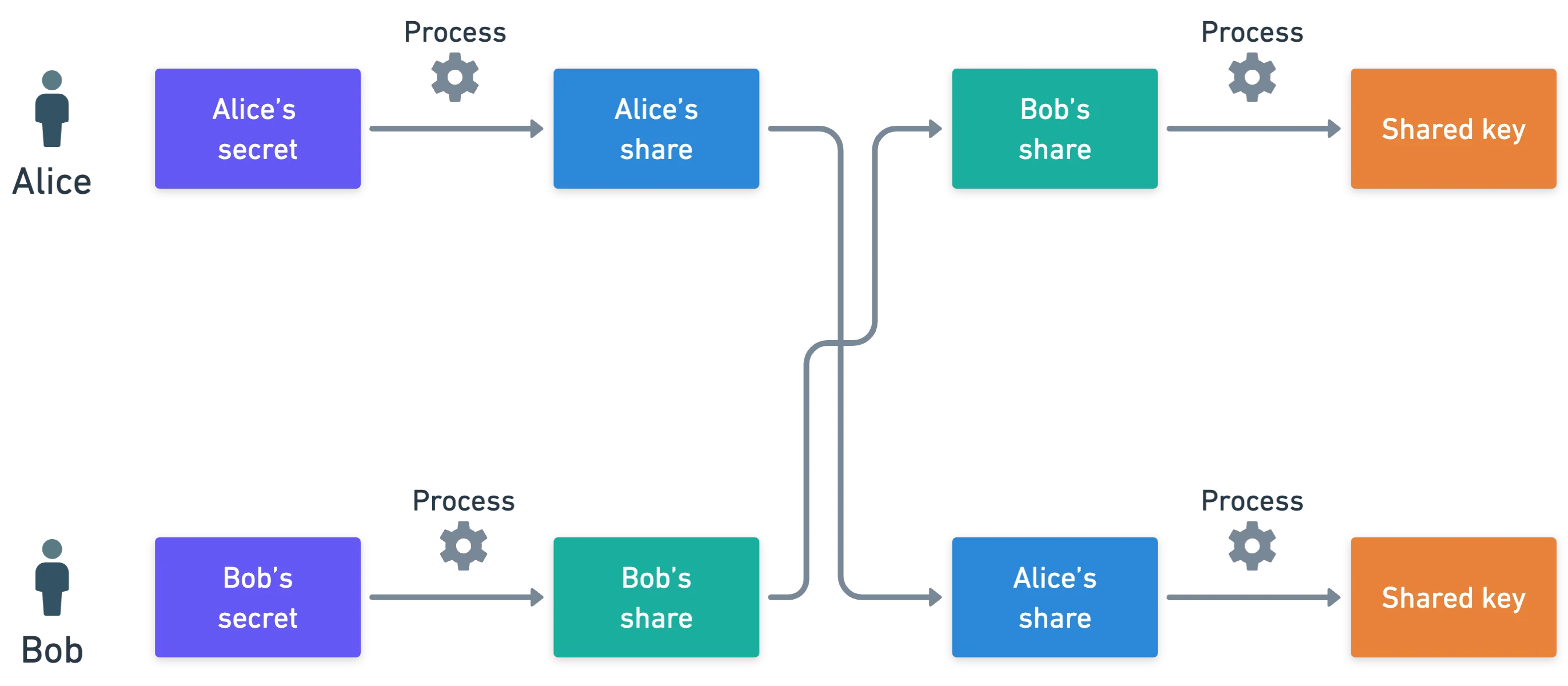
La idea es simple: Alicia y Bruno quieren combinar sus secretos individuales para producir una clave compartida.

Creando el Secreto Compartido

Para hacer esto, Alicia y Bruno acuerdan una curva elíptica para usar, y algún generador $G$ para la curva. Digamos que Alicia elige un entero secreto $a$, y Bruno elige otro entero secreto $b$. ¿Cómo los combinan?  - Alicia calcula $A = [a]G$, y envía eso a Bruno. Recuerda que Bruno no puede recuperar $a$ a partir de $A$ — es extremadamente difícil.

• Bruno recibe $A$ y calcula $S = [b]A = [b]([a]G) = [b.a]G$.

Bruno también envía $B = [b]G$, y Alicia también calcula $S = [a]B = [a]([b]G) = [b.a]G$. ¡Y mira eso — ambos han calculado el mismo punto $S$!

Lo interesante de esto es que cualquiera que intercepte las comunicaciones entre Alicia y Bruno solo obtendría $A$ o $B$. Y por sí solos, estos puntos no significan nada.

¡Así de simple, han creado una clave compartida de manera segura! Sensacional. Solo recuerda mantener la clave generada a salvo.

Esquemas de Compromiso

Muy bien, ya sabemos cómo generar una clave compartida de forma segura. ¿Qué más podemos hacer?

Otra idea es la de comprometerse con un valor por adelantado. Y para ilustrarlo, juguemos a piedra, papel, o tijera. Pero juguémoslo por turnos. Así es como sería:

Alicia juega piedra. Luego Bruno juega papel. La victoria más fácil de su vida.

Obviamente, el problema aquí es que Alicia reveló su jugada por adelantado. ¿Pero qué pasaría si pudiera ocultar su jugada?

Click to zoom

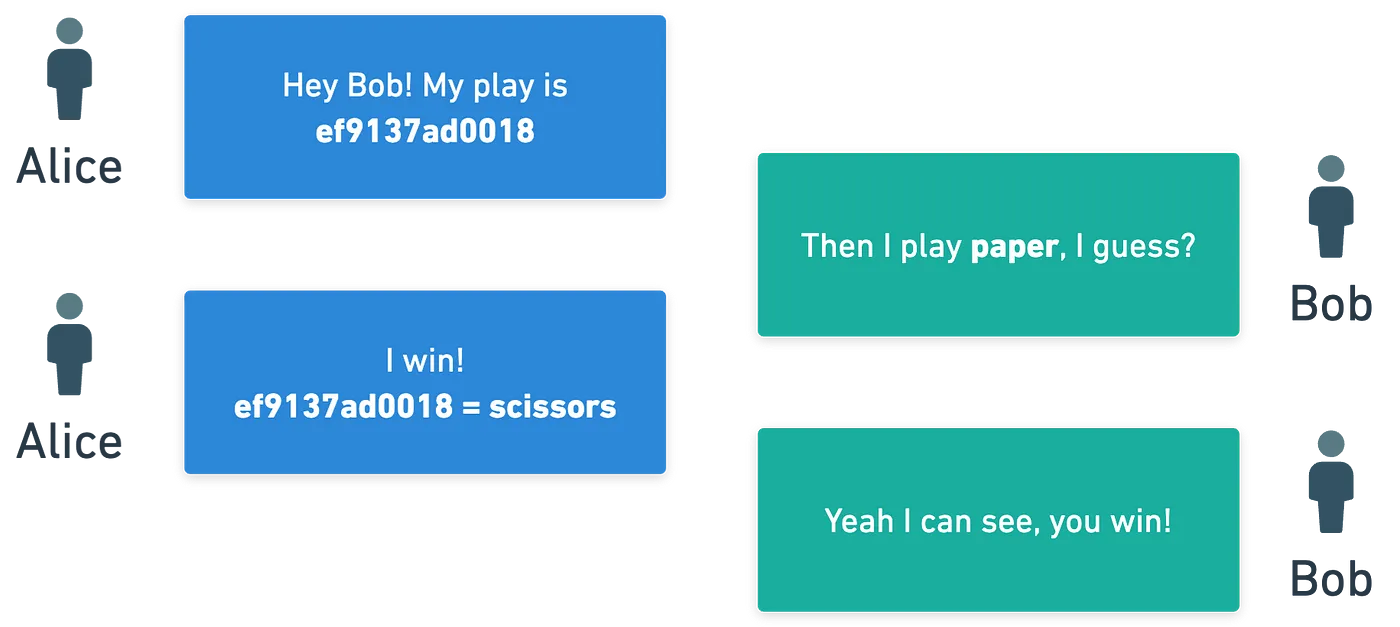
Alicia produce algún valor que está vinculado a su jugada (tijeras), pero que también oculta su decisión. Esto se conoce como un compromiso. Más tarde, Alicia revela el valor original, y Bruno verifica que coincida con el compromiso. Es realmente como poner tu jugada en un sobre sellado, y abrirlo cuando sea necesario.

Sé lo que estás pensando: ¿por qué diablos alguien jugaría piedra, papel, o tijera de esta manera? Realmente no lo sé. Pero ese no es el punto — podemos usar esta idea para crear protocolos útiles.

Creando el Compromiso

Vamos a construir lo que se llama un compromiso de Pedersen. Este tipo de esquema requiere un paso de configuración, que debería devolver un generador $G$ de un grupo de curva elíptica, y algún otro punto $H = [k]G$.

$$\textrm{setup}() \rightarrow (G, H)$$

Luego, si Alicia quiere comprometerse con algún mensaje $M$, sigue estos pasos:

• Hace hash del valor a un entero $h(M)$,
• Luego elige un entero aleatorio $r$, también llamado factor de cegado,
• Finalmente, calcula $C = [r]G + [h(M)]H$. Este será su compromiso.

El compromiso $C$ puede compartirse con cualquiera, porque es ocultante: no revela información sobre el mensaje. Más tarde, Alicia puede compartir los valores secretos $M$ y $r$, y cualquiera (por ejemplo, Bruno) puede recalcular $C$ y verificar que coincida con lo que Alicia compartió — decimos que Alicia abre el compromiso.

Formalmente, decimos que un esquema de compromiso debe ser:

• Ocultante: no debe revelar información sobre el mensaje comprometido.
• Vinculante: el compromiso solo puede abrirse con los $M$ y $r$ originales. De lo contrario, debería ser inválido.

Y finalmente, ¿qué hay del factor de cegado? Si no lo usamos, entonces $C$ siempre se vería así: $C = [h(M)]H$. Esto no es bueno, porque la función de hash es determinista: siempre producirá el mismo resultado para una entrada fija.

Así que tan pronto como veas dos compromisos idénticos, inmediatamente sabrás que están asociados a la misma información — y si ya conoces los datos secretos, ¡entonces el compromiso no oculta nada! Recuerda:

Una cadena es tan fuerte como su eslabón más débil

La introducción de un factor de cegado aleatorio soluciona este problema. En general, esta idea de introducir aleatoriedad en los esquemas se utiliza para prevenir vulnerabilidades basadas en la repetición, como la que acabamos de describir.

Los esquemas de compromiso son una piedra angular para construcciones más poderosas que exploraremos en artículos posteriores.

Firmas

Ya hemos cubierto anteriormente un ejemplo de firmas utilizando curvas elípticas, llamado Algoritmo de Firma Digital de Curva Elíptica (o ECDSA para abreviar). Pero hay otras formas de crear firmas.

En particular, existe otro protocolo llamado firma de Schnorr. Y a decir verdad, es más simple que ECDSA. Pensándolo bien, tal vez deberíamos haber cubierto esto en lugar de ECDSA. Sí. Lo siento por eso.

De todos modos, la firma de Schnorr a menudo se presenta utilizando el grupo aditivo de enteros módulo $q$, pero como mencionamos anteriormente, cualquier construcción con dicho grupo puede adaptarse a curvas elípticas. Y esto es lo que vamos a demostrar ahora.

La configuración es la misma que antes, en ECDSA: Alicia tiene una clave privada $d$, y Harold (lo siento Bruno, le debemos al menos esto) tiene la clave pública asociada $Q = [d]G$, donde $G$ es un generador de grupo sobre el que Alicia y Harold han acordado.

Para firmar, Alicia hace lo siguiente:

• Elige un entero aleatorio $r$ y calcula $R = [r]G$.
• Luego, calcula el hash $e = H(R || M)$. Aquí, $||$ representa la concatenación bit a bit — básicamente ella sólo hace hash de un montón de ceros y unos. Ah, y $e$ es un entero.
• Finalmente, calcula $s = r - e.d$.

La firma es el par $(s, e)$. Para verificar, Harold sigue este procedimiento:

• Calcula $R' = [s]G + [e]Q$,
• Y acepta si $e = H(R' || M)$.

Simple, ¿verdad? Esta vez, no necesitamos calcular ningún inverso multiplicativo modular. Y es bastante sencillo comprobar que $R'$ debería coincidir con $R$:

$$R' = [s]G + [e]Q = [r - e.d + e.d]G = [r]G = R$$

Las firmas de Schnorr ofrecen una alternativa a las ECDSA más establecidas. De hecho, son más sencillas de implementar, no dependen de inversos multiplicativos modulares y teóricamente ofrecen más seguridad. Algunas blockchains como Polkadot ya han adoptado este esquema de firma; al final, depende de ti decidir qué usar.

Pruebas de Conocimiento Cero

Las pruebas de conocimiento cero (ZKP para abreviar, por su sigla en inglés) han sido un tema candente en los últimos años. No son un descubrimiento nuevo en absoluto, pero han recibido mucho interés debido a sus propiedades y las cosas interesantes que se pueden hacer con ellas.

Esencialmente, una ZKP es una forma de demostrar o probar conocimiento de algo, sin revelar nada sobre ello. Suena loco, ¿verdad? ¿Cómo puedo decirte que sé algo sin decirte qué es ese algo?

Aquí hay un excelente video que muestra algunos excelentes ejemplos de ZKPs.

El ejemplo que más me gusta es la prueba de ¿Dónde está Wally?: lo que quiero probar es que sé dónde está Wally. Una opción es simplemente señalarlo — ¡pero esto revelaría irrevocablemente su ubicación!

Para no revelar su ubicación, puedo hacer lo siguiente: tomar un trozo grande de cartón, hacer un agujero del tamaño de Wally, y colocarlo sobre el libro. ¡Puedes ver a Wally a través del agujero, pero no puedes ver dónde está colocado en la página!

El Protocolo de Schnorr

Claramente, no vamos a construir un sistema de prueba de localización de Wally con curvas elípticas. Tendremos que contentarnos con algo mucho más simple: probar el conocimiento del logaritmo discreto de un punto. Esto es, probar que conocemos algún valor $x$, tal que $Y = [x]G$, siendo $G$ un generador de un grupo de curva elíptica. El grupo tiene orden $n$.

Lo que estamos a punto de describir se llama el protocolo de Schnorr, adaptado a curvas elípticas. Es un protocolo muy simple y elegante, y proporciona una gran base para pruebas de conocimiento más complejas.

Aquí está Claus P. Schnorr, por cierto. Con sus 80 años de edad. Toda una leyenda.

Así es como funciona el protocolo: Alicia, a quien llamaremos el probador, quiere probar que conoce $x$. Bruno, el verificador, conoce $Y$. Por supuesto, Alicia podría revelar el valor de $x$, y Bruno podría verificar que efectivamente es el logaritmo discreto de $Y$ ($Y = [x]G$). Pero por cualquier razón, digamos que $x$ debe permanecer privado.

Alicia y Bruno interactúan de la siguiente manera:

• Alicia primero elige algún entero aleatorio $r$, y calcula $R = [r]G$. Este es un compromiso que luego envía a Bruno.
• Bruno elige algún otro entero $c$ al azar, y lo envía a Alicia.
• Alicia luego calcula:

$$s = (r + c.x) \ \textrm{mod} \ n$$

• Bruno recibe $s$, y verifica si:

$$[s]G = R + [c]Y$$

¡Te dejo las matemáticas para que las compruebes!

Lo interesante es que, si por alguna razón Bruno no está convencido después de esto, puede enviar un valor fresco de $c$ a Alicia, y repetir el proceso. De hecho, puede hacer esto tantas veces como quiera hasta que esté satisfecho. Esto sugiere la idea de que algunos protocolos criptográficos son interactivos, un hecho al que volveremos más adelante en la serie.

Funciones Aleatorias Verificables

Otra cosa genial que podemos hacer es generar números aleatorios de manera verificable.

¿Qué?

Esta suena realmente loca. Creo que una analogía puede ayudar.

Supongamos que compras un boleto de lotería. Vas a una tienda, eliges alguna combinación aleatoria de números, y recibes el boleto asociado.

Luego se selecciona el ganador de la lotería, ¡y resulta que es tu número! ¿Cómo pruebas que eres el ganador? Bueno, por supuesto, ¡tienes el boleto! Así que simplemente lo presentas en la casa de lotería, ¡y obtienes tu premio!

Aunque esta analogía no es perfecta, transmite un mensaje importante: puede haber cosas que probar acerca de números generados aleatoriamente.

Las funciones aleatorias verificables (o VRFs para abreviar) hacen exactamente eso: generan un número pseudoaleatorio basado en alguna entrada de un usuario, y también proporcionan una prueba de que el proceso de generación fue honesto y correcto. Discutiremos esto con más detalle en artículos posteriores, así que por ahora, concentrémonos en una implementación de VRFs utilizando solo curvas elípticas.

Así, la intención al crear una VRF es la siguiente: Alicia quiere generar un número pseudoaleatorio, que Bruno pueda verificar. Acuerdan un generador de curva elíptica $G$ para un grupo de orden $n$, y también acuerdan dos algoritmos: $h$ y $h'$. El primero hace hash a un número, como es habitual, pero el segundo hace hash a un punto en la curva elíptica.

La configuración no diverge demasiado de lo habitual: Alicia tiene una clave privada $d$, y una clave pública $Q = [d]G$. Sin embargo, hay un elemento extra aquí: la entrada $a$ a la VRF es públicamente conocida. Todos ejecutarán el mismo número a través de sus VRFs independientes, y producirán diferentes salidas.

Ahora, hay dos pasos en el algoritmo: un paso de evaluación, donde se produce el número aleatorio junto con una prueba, y el paso de verificación. Alicia realiza la evaluación de la siguiente manera:

• Calcula $H = h'(Q, a)$. Este es un punto en la curva elíptica.
• Luego calcula $Z = [d]H$, la salida VRF.
• Ahora tiene que producir una prueba. Elige un número aleatorio $r$, y calcula $U = [r]G$, y $V = [r]H$.
• Hace hash de todo en un número $c$:

$$c = h(H || Z || U || V)$$

• Finalmente, calcula $s$:

$$s = r + d.c \ \textrm{mod} \ n$$

El resultado de la evaluación VRF es $\pi = (Z, c, s)$, donde $Z$ es la salida pseudoaleatoria actual, y los otros valores funcionan como una prueba de correctitud de $Z$.

Finalmente, Bruno necesita verificar la prueba. Esto es lo que hace:

• Calcula el mismo hash que calculó Alicia, $H = h'(Q, a)$. Puede hacer esto porque tanto $Q$ como $a$ son públicos.
• Luego calcula $U'$ y $V'$ como se muestra a continuación. Puedes comprobar que estos resultan en los mismos $U$ y $V$ de antes.

$$\\ U' = [s]G - [c]Q \\ V' = [s]H - [c]Z$$

 - Finalmente, calcula $c' = h(H || Z || U' || V')$, y acepta la prueba si $c = c'$.

Uf. Está bien. Eso fue mucho. Vamos a descomprimirlo.

La idea es que la salida $Z$ es impredecible debido a la naturaleza de la función de hash, pero es determinista no obstante. Debido a esto, somos capaces de producir una firma corta que solo puede funcionar con el conocimiento de la clave privada, $d$.

La utilidad de las VRFs puede no ser inmediatamente evidente, pero pueden ser una herramienta poderosa para la aplicación correcta. Por ejemplo, Algorand utiliza VRFs como parte de su mecanismo de consenso central. ¡Y quién sabe qué aplicaciones locas puedes encontrar para ellas! El mundo es tu ostra, siempre que tengas las herramientas adecuadas.

Resumen

Como puedes ver en los métodos que hemos explorado, algunas ideas se repiten una y otra vez. En la mayoría de los casos, realizamos dos operaciones que producen el mismo resultado. También comenzamos desde un par de claves privada/pública la mayoría de las veces. Usamos funciones hash para mapear datos en conjuntos de interés.

Combinar estas ideas básicas permite la creación de protocolos interesantes y útiles, y eso es todo. Aplicaciones más complejas pueden requerir "juegos" criptográficos más complejos.

Y por supuesto, hay más cosas divertidas que podemos hacer con curvas elípticas. Por ejemplo, existen esquemas de firma más sofisticados, como firmas ciegas, firmas en anillo, firmas de umbral, entre otras. Cubriremos esas en el próximo artículo.