Criptografía 101: Curvas Elípticas (Algo) Desmitificadas

Este artículo forma parte de una serie más larga sobre criptografía. Si este es el primer artículo con el que te encuentras, te recomiendo comenzar desde el principio de la serie.

En el artículo anterior, discutimos brevemente algunas de las ideas que sustentan una buena parte de las técnicas criptográficas más utilizadas.

Aún no hemos discutido por qué los grupos y la aritmética modular son útiles para la criptografía. Como seguramente puedes imaginar, la idea general es que nos permiten crear problemas que son tan difíciles de resolver, que es prácticamente imposible descifrarlos incluso a coste de cantidades gigantes de recursos computacionales. Entonces, por ejemplo, ¿por qué funciona una firma digital? Bueno, porque producir una firma válida es bastante simple con el conocimiento de una clave secreta, pero increíblemente difícil sin ella.

Nos ocuparemos de estas consideraciones más adelante. Por ahora, creo que es más fructífero enfocarnos en otros grupos que ayudan a hacer que los problemas a resolver sean aún más difíciles — y aquí es donde las curvas elípticas entran en escena.

¿Qué son las Curvas Elípticas?

Una curva generalmente se define mediante una ecuación. En el caso de las curvas elípticas, la ecuación $E$ (que en realidad es una forma reducida, pero la utilizaremos igualmente) se ve así:

E: y^2 = x^3 + ax + b

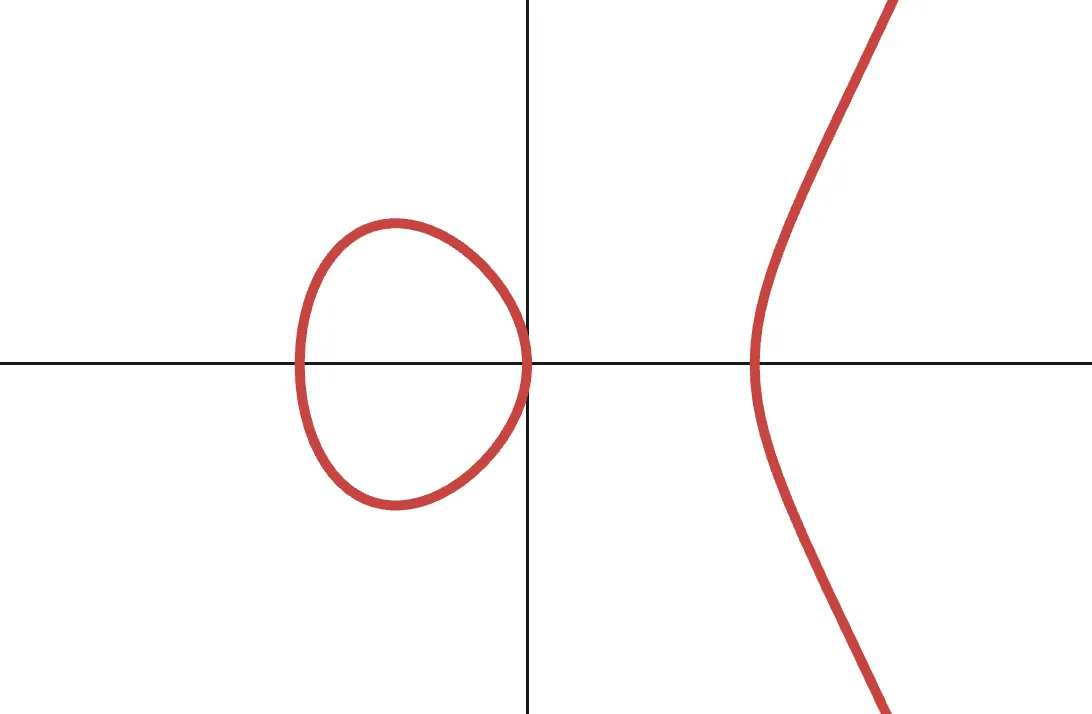
Una curva elíptica — Un gráfico de la curva y² = x³ - x

Pero espera... ¿Qué tiene esto que ver con los grupos? ¡Esto es solo una curva después de todo!

Recapitulemos lo que hemos aprendido hasta ahora. Un grupo se define por un conjunto (llamémoslo $\mathbb{G}$ ), y una operación binaria que involucra dos elementos de $\mathbb{G}$ , y produce un resultado que también está en $\mathbb{G}$ . Si podemos pensar en una manera de usar curvas elípticas para obtener un conjunto y una operación binaria válidos, entonces encontramos un grupo.

Y cómo no, ¡existe una manera de hacer esto!

•••

La Operación de Grupo

Toma dos puntos cualesquiera $P$ y $Q$ en la curva elíptica, luego dibuja una línea a través de esos puntos. Algunas sustituciones básicas muestran que (casi siempre) existirá un tercer punto de intersección. Luego toma ese punto, imagina que el eje $x$ es un espejo, y refléjalo verticalmente. ¡Felicidades, acabas de llegar al punto $R = P + Q$ !

Este proceso se llama la regla de la cuerda y la tangente. Y es, de hecho, la operación de grupo que estamos buscando.

La primera vez que vi esto, recuerdo haber pensado "qué proceso tan extraño". Recuerdo haberme preguntado: ¿por qué diablos necesito reflejar el tercer punto de intersección? Y después de profundizar más en el tema, todo lo que puedo decir es esto: explicar la razón por la que esto tiene sentido está muy lejos del alcance de este artículo. Solo voy a pedirte que confíes en que todo es perfectamente lógico, al menos por ahora.

Diagrama de cuerda y tangente — La curva elíptica y² = x³ - x + 1 (roja) con una representación de la operación P + Q = R

Puedes probar esto tú mismo en una herramienta gráfica como Desmos o GeoGebra.

Un componente resuelto, pero todavía queda uno más — también necesitamos un conjunto. Y dado que la regla de la cuerda y la tangente mapea dos puntos en la curva elíptica a otro, se deduce naturalmente que estaremos trabajando con un conjunto de puntos en la curva elíptica. Pero hay dos problemas con esto, que son:

La mayoría de los puntos en la curva elíptica tienen valores reales, lo que significa que las coordenadas pueden no ser números enteros. Y es importante que lo sean: de lo contrario, podríamos tener errores de redondeo al calcular $P + Q$ .
Hay un número infinito de puntos en la curva, y buscamos un conjunto finito.

Entonces, ¿cómo resolvemos estos problemas?

Encontrando un Conjunto Adecuado

Resulta que algunas curvas elípticas tienen un número infinito de puntos con valores enteros, es decir, puntos como $P = (1,2)$ . Debido a esto, nuestro primer problema desaparece de manera algo mágica con una selección adecuada de la curva elíptica. Asumamos que sabemos cómo hacer eso, y concentrémonos en el segundo problema.

Hay un truco ingenioso para convertir una cantidad infinita de enteros en un conjunto finito, y ya lo hemos visto en acción. ¿Puedes adivinarlo? Así es, ¡la operación módulo!

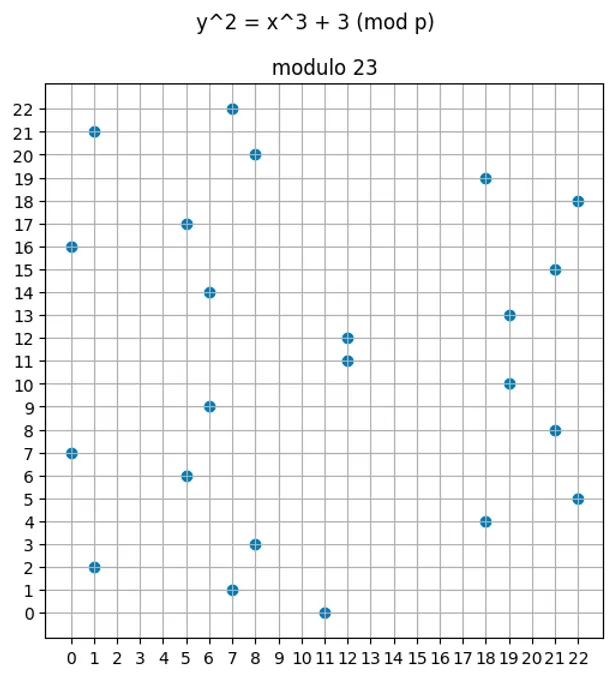
Cómo se ve una curva elíptica sobre los enteros (módulo 23) — Los puntos de una curva elíptica, módulo 23

Formalmente, decimos que la curva elíptica está definida sobre un campo finito, por lo que cualquier punto que esté "fuera de rango" simplemente se mapea de vuelta al rango con la operación módulo. Esto se denota como:

E(\mathbb{F_q}) \ / \ \mathbb{F}_q = \{0,1,2,3,...,q-1\}

¡Y ahí lo tienes! Ahora tenemos un conjunto y una forma de calcular el resultado de "sumar" dos puntos. Pero, ¿y eso es todo? Algo parece faltar...

La Identidad del Grupo

Mira la siguiente imagen. ¿Qué sucede si intentamos sumar $P + Q$ en este escenario?

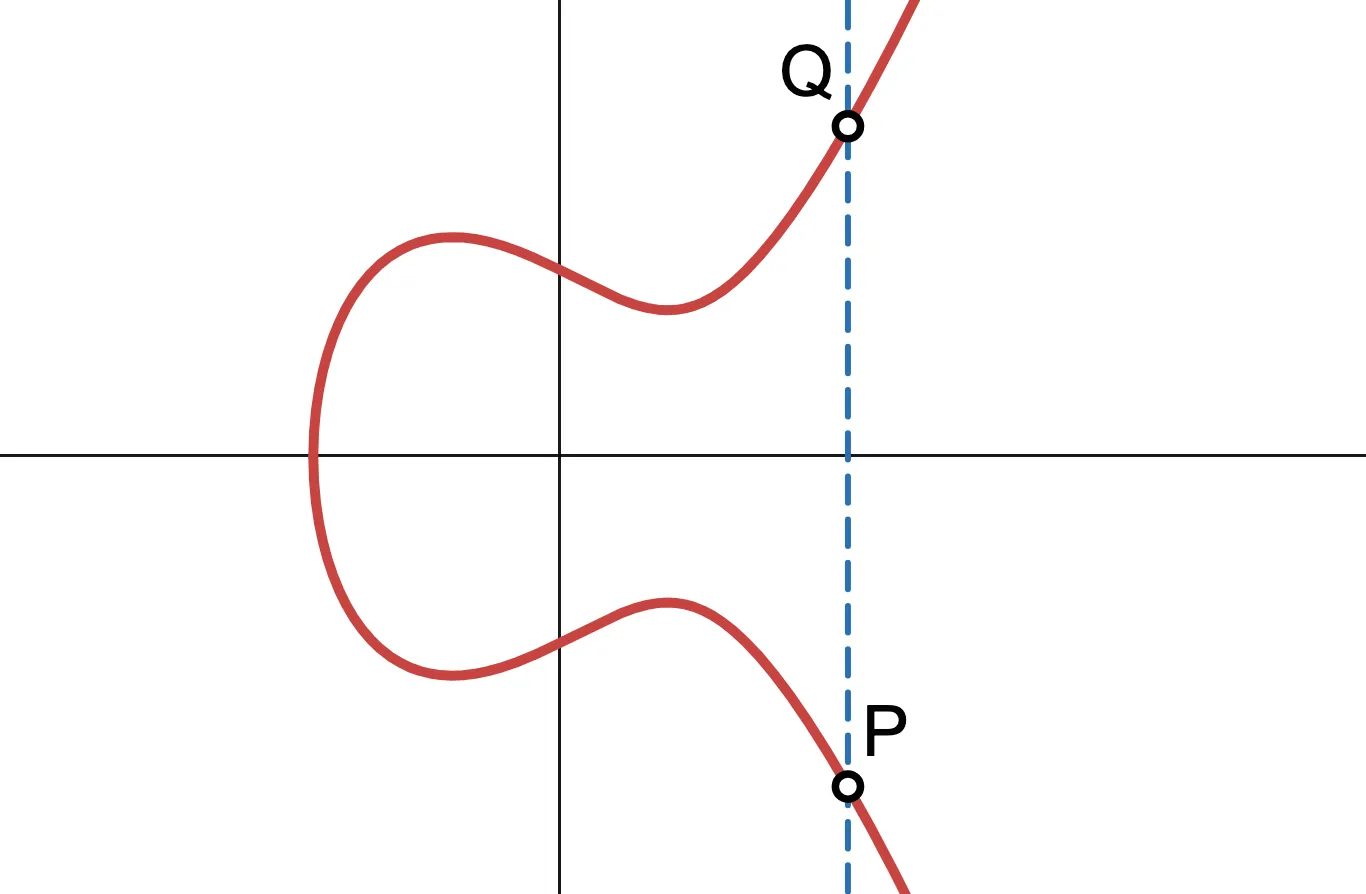
Dos puntos alineados verticalmente sumados entre sí

¡Podemos ver inmediatamente que no hay un tercer punto de intersección! El pánico crece. ¿Significa esto que nuestra construcción no funciona?

Afortunadamente, la crisis se evita fácilmente definiendo un nuevo elemento del grupo, denotado $\mathcal{O}$ . Piensa en él como un punto en el infinito — que no es realmente lo que sucede, pero puede ayudar a la conceptualización. Este nuevo elemento tiene una propiedad interesante: dado cualquier punto $P$ en la curva:

P + \mathcal{O} = \mathcal{O} + P = P

¿No te suena familiar? ¿No es esto exactamente lo que sucede cuando sumamos cero a cualquier número?

En efecto, este comportamiento es importante en la teoría de grupos: el papel que el cero juega en el grupo de los enteros, y el papel que $\mathcal{O}$ juega en las curvas elípticas es el de la identidad de los respectivos grupos. Agregar este elemento a nuestro conjunto lo hace completo, y ahora podemos sumar dos puntos y siempre tener un resultado válido.

Sin embargo, no hemos terminado. Hay un pequeño detalle más que debemos cubrir.

Duplicación de Puntos

¿Qué sucede si intentamos sumar $P + P$ ? Para intentar seguir la regla de la cuerda y la tangente: necesitamos una línea a través de los dos puntos en la operación, pero aquí... ¡Solo hay uno! Así que, como sugiere el nombre, necesitaremos considerar la línea tangente a la curva elíptica en $P$ .

Como antes, encontramos otro punto de intersección, lo volteamos y encontramos $P + P$ , que convencionalmente denotaremos $[2]P$ . En un golpe absoluto de inspiración, esta operación fue nombrada duplicación de punto.

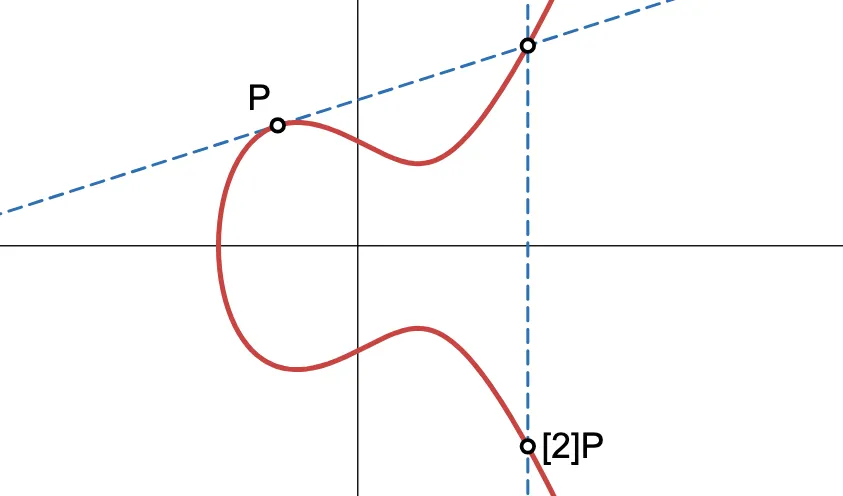
Para calcular $P + [2]P$ se procede como de costumbre: dibuja una línea a través de los dos puntos, refleja el tercer punto de intersección, ¡y voilà! Acabas de obtener $[3]P$ . Haz esto de nuevo, y obtendrás $[4]P$ . Y aquí, podemos observar algo peculiar: sumar $P$ cuatro veces ( $P + P + P + P$ ) produce el mismo resultado que sumar $[2]P + [2]P$ !

Por inocente que parezca la declaración anterior, es en realidad la herramienta más poderosa que tenemos cuando trabajamos con curvas elípticas. Supongamos que queremos calcular $[12384162178627301263]P$ . Hacer esto punto por punto tomaría muchísimo tiempo, pero al aplicar correctamente la duplicación de puntos, ¡el resultado puede obtenerse exponencialmente más rápido!

Esto es un pequeño guiño a los problemas extremadamente difíciles que se mencionaron al principio de este artículo. Y como pronto discutiremos, ¡esto es precisamente el tipo de problemas difíciles que permiten que existan construcciones criptográficas basadas en grupos!

•••

Resumen {##summary}

Acabamos de definir los grupos de curvas elípticas. Son simplemente un conjunto de puntos enteros, que podemos sumar, y que están dentro de un rango gracias a la operación módulo. Usualmente, cuando se mencionan curvas elípticas en la literatura, se refiere al grupo, no a la curva. Si la curva necesita una mención específica, a menudo se la llama curva afín.

Si te sientes así en este momento:

Meme de 'No tengo idea de lo que estoy haciendo' — Yo cada mañana

Todo lo que puedo decir es que esto puede ser difícil de comprender en un primer contacto, pero una vez que lo asimilas, se siente bastante natural. Date algo de tiempo, ¡y no dudes en contactarme si tienes alguna pregunta!

Además, puedes experimentar con curvas elípticas en este sitio web.

Nuestra base está lista. En el próximo artículo, examinaremos qué podemos hacer con nuestro conocimiento de las curvas elípticas. Veremos un esquema para cifrado asimétrico y otro para firmas digitales. ¡Mantente atento!