Criptografía 101: Encriptación y Firmas Digitales

Este artículo forma parte de una serie más larga sobre criptografía. Si este es el primer artículo con el que te encuentras, te recomiendo comenzar desde el principio de la serie.

En la entrega anterior, ampliamos nuestro conocimiento básico de grupos definiendo grupos de curvas elípticas. Y mencionamos brevemente que estos conceptos nos permitirían construir algunos mecanismos criptográficos útiles.

Y como prometimos, veremos dos ejemplos de tales técnicas básicas: una para firma digital y otra para encriptación. Pero antes de hacerlo, necesitamos definir un par de herramientas que serán esenciales en nuestro desarrollo. Trabajaremos en el contexto de las curvas elípticas, pero estos conceptos pueden generalizarse a otros grupos.

Probablemente hayas oído hablar de claves privadas y públicas. Veamos qué son realmente.

Pares de Claves

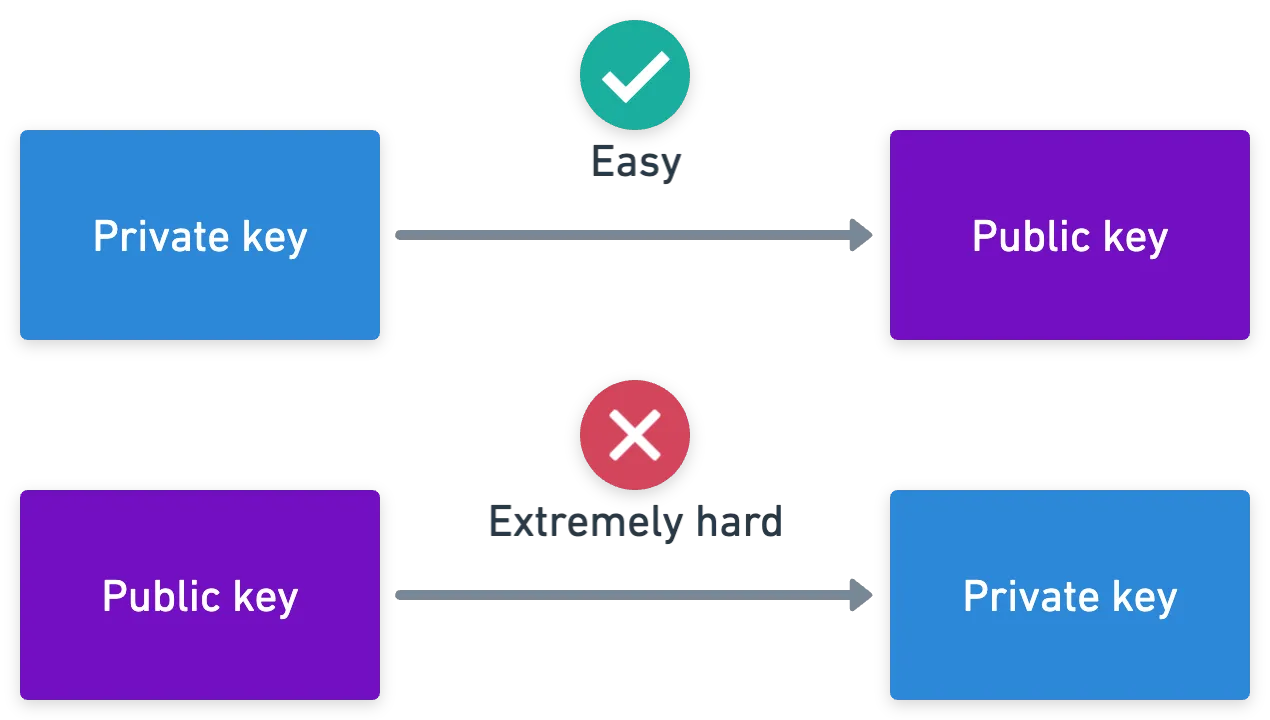
La historia que generalmente se cuenta cuando se aprende sobre firmas digitales va más o menos así: un usuario (digamos, Alicia) con una clave privada (o secreta) puede firmar un mensaje, y luego cualquiera puede verificar la firma con la clave pública asociada.

Y por supuesto, no aprendemos nada sobre los mecanismos detrás de esto. Pero hay un mensaje implícito: no debería ser posible obtener una clave privada a partir de una clave pública, ya que esto significaría que cualquier persona que tenga la clave pública de Alicia podría producir una firma en nombre de Alicia (se llama privada por una razón, después de todo). Con esto en mente, veamos qué son realmente estas claves.

Click to zoom

¿Recuerdas los generadores de grupo del primer artículo? ¡Bueno, aquí es donde entran en juego! ¡Las curvas elípticas, al ser grupos, también tienen generadores y subgrupos!

Supongamos que Alicia y otro tipo, Bruno, acuerdan un punto generador $G$ en la curva elíptica. Alicia luego elige algún número aleatorio $d$ del conjunto de enteros módulo $q$, así que $d < q$. Además, asumamos que $d$ es un número grande, no solo $12$ o $35$. Esta será su clave privada.

Alicia procede a calcular $Q = [d]G$, aprovechando el poder de la duplicación de puntos, y obtiene otro punto en el grupo — esta será su clave pública, y puede enviarla de manera segura a Bruno.

Evidentemente, $Q$ codifica información sobre la clave privada. Bruno podría intentar calcular un número $d$ tal que $Q = [d]G$ — pero el problema es que, si nuestro grupo de curvas elípticas es "lo suficientemente grande", eso le tomaría a Bruno un tiempo realmente largo. Y esto es precisamente la salsa secreta: encontrar $d$, incluso conociendo $Q$ y $G$, debería ser casi imposible. Esto se conoce como (una versión del) problema del logaritmo discreto (DLP por su sigla en inglés).

Por supuesto, si nuestro grupo resulta tener $1000$ elementos, o si el número que Alicia elige es "pequeño", probar posibles valores de $d$ es una tarea factible. Probablemente puedas escribir un script que resuelva el problema en menos de 10 minutos — esto se llama fuerza bruta. El problema DLP realmente brilla cuando tenemos grupos enormes. Por ejemplo, la curva 25519 tiene subgrupos de orden alrededor de $~2^{250}$. Eso es un número bastante grande. Buena suerte tratando de obtener $d$ por fuerza bruta.

Encriptación

Alicia ahora tiene un número $d$ como su clave privada, y Bruno tiene la clave pública correspondiente $Q$, que es solo un punto en la curva elíptica. ¿Qué pueden hacer con esto?

Estas herramientas que desarrollamos son suficientes para empezar a construir cosas divertidas (¡hurra!). ¡Vamos a encriptar algunos datos!

Imagina que Bruno quiere proteger un mensaje para que Alicia sea la única persona que pueda leerlo. Si fueran adolescentes en la escuela, podrían intercambiar un mensaje escrito en un código secreto que solo Alicia y Bruno pueden entender. Como ambos conocen el código secreto, ambos pueden "deshacer" la codificación — así que esto se llama encriptación simétrica.

Muy bien, ¡suena bastante simple!

¿Cómo sucede esto en una aplicación real? Piensa en esto: cualquier mensaje es solo un montón de ceros y unos, algún número binario. Si distorsionamos dicho número, lo transformamos esencialmente en un lío sin mucho sentido — esto generalmente se llama texto cifrado. Y si lo hacemos de manera reversible, ¡el mensaje original puede recuperarse!

Click to zoom

Aquí hay una implementación simple en caso de que quieras experimentar con ella.

Solo para aclarar, la reversibilidad aquí está dada por la operación lógica XOR. No te preocupes por esto - el punto es que pudimos enmascarar el mensaje original, con una clave secreta compartida.

¿Qué Hay de las Curvas Elípticas?

Claramente, no necesitamos curvas elípticas en la construcción anterior. Y esto demuestra que la criptografía es mucho más amplia que solo una herramienta, y realmente se remonta a mucho antes de que las curvas elípticas fueran siquiera una cosa.

Pero, ¿qué pasa con la clave secreta? ¿Cómo acuerdan Alicia y Bruno una clave compartida? Si lo hacen de manera insegura, entonces alguien más podría estar escuchando, y esa tercera persona (digamos Carlos) puede entonces leer los mensajes secretos de Alicia y Bruno! No es genial, ¡nuestra encriptación se vuelve inútil!

No entremos en pánico todavía. Aunque hay formas de compartir claves secretas de manera segura, hay otra forma de abordar esto: podemos usar curvas elípticas para obtener el secreto compartido de manera asimétrica.

Encriptación Asimétrica

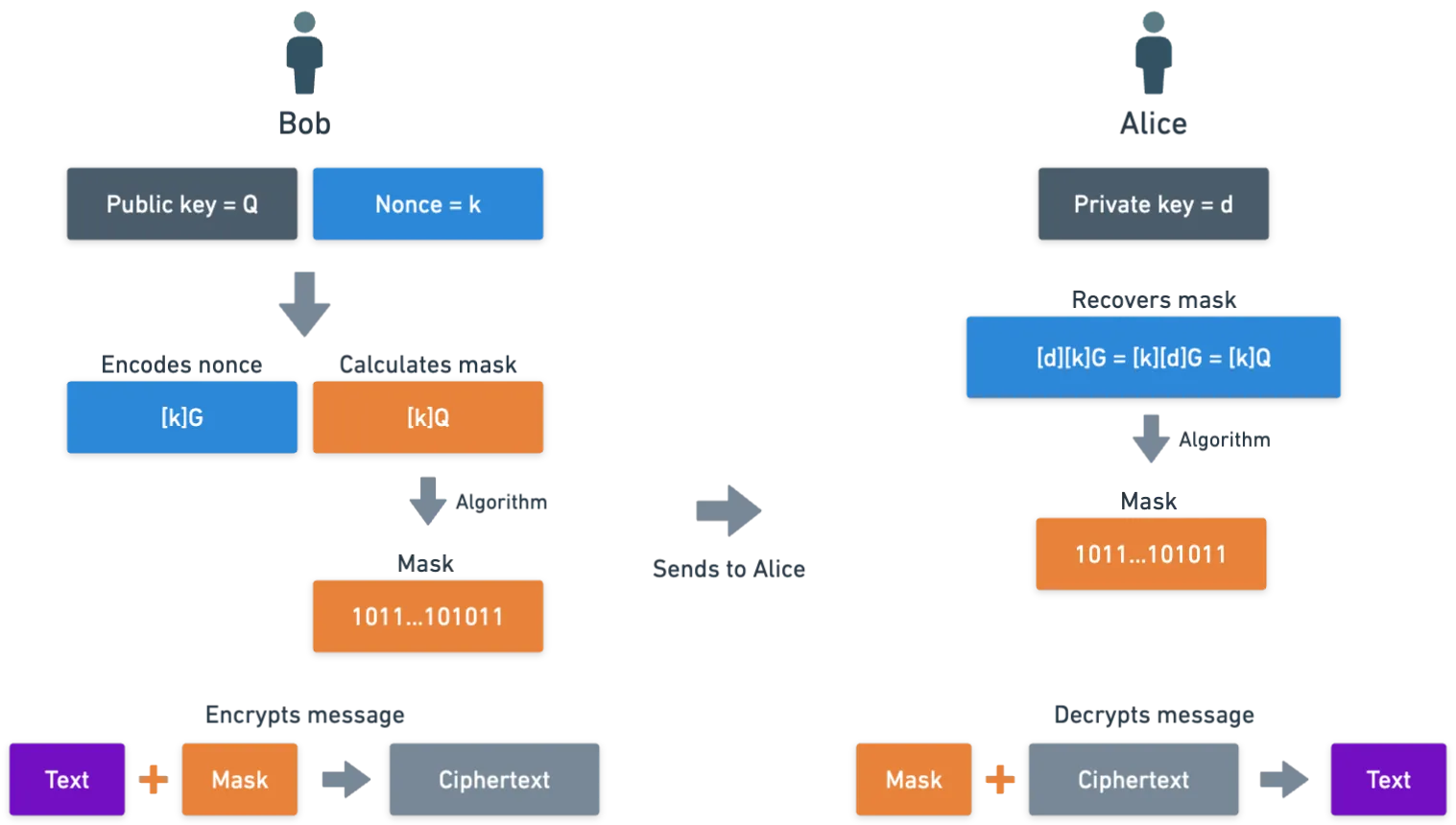
Digamos que Bruno quiere encriptar un mensaje $M$ para Alicia. En lugar de acordar una clave, Alicia puede simplemente elegir una clave privada $d$ y compartir su clave pública $Q = [d]G$ con Bruno. Con esta configuración, podemos idear una forma para que Bruno encripte mensajes solo para Alicia. Así es como va:

• Él elige algún número aleatorio $k < q$, generalmente llamado nonce,
• Bruno luego calcula $[k]Q$, y usa esto para calcular una máscara, que denotaremos $P$, usando algún algoritmo acordado,
• Enmascara el mensaje usando XOR como en el ejemplo anterior, y obtiene el texto cifrado $C = M + P$,
• Finalmente, calcula $[k]G$, donde $G$ es el generador de grupo en el que Alicia y Bruno acordaron previamente,
• Bruno luego envía el par de puntos $([k]G, C)$ a Alicia.

Alicia, que conoce la clave privada $d$, puede realizar estas acciones:

• Calcula $[d]([k]G)$. No lo mencionamos, pero la multiplicación es conmutativa en curvas elípticas, así que $[d]([k]G) = [k]([d]G) = [k]Q$. Sin conocimiento de $k$, aún podemos reconstruir la máscara que usó Bruno. Asombroso.
• Usando el algoritmo acordado, Alicia calcula la máscara y revierte el enmascaramiento con $M = C + P$.

Los elementos visuales tienden a ayudar mucho. En general, el proceso se ve así:

Click to zoom

Este proceso se llama Esquema de Encriptación Integrada de Curva Elíptica, o ECIES para abreviar. Existen otros esquemas similares, como el sistema de encriptación de ElGamal, que puede adaptarse a curvas elípticas.

No sé tú, pero yo encuentro esto fascinante. Con solo un par de operaciones, es posible proteger datos de una manera que es imposible de descifrar en la práctica sin el conocimiento de un solo número (que solo Alicia conoce).

¡Nuestra comprensión de los grupos finalmente está dando dividendos!

Resumiendo:

Este método de encriptación funciona calculando una máscara y agregándola al mensaje original.

En la encriptación simétrica, ambas partes necesitan conocer la máscara; en la encriptación asimétrica, el desenmascaramiento solo puede realizarse con el conocimiento de una clave privada por una de las partes.

Firmas Digitales

La encriptación asume que la información codificada debe permanecer en secreto para lectores no deseados. Esto no siempre es cierto: a veces la información puede ser pública, pero nuestro interés radica en probar su autenticidad. Por ejemplo:

Supongamos que Bruno quiere enviar una solicitud de pago a Alicia por $1000. Le envía a Alicia su número de cuenta bancaria y la cantidad que necesita transferir. ¿Qué pasaría si alguien más (digamos Carlos) intercepta el mensaje y cambia la cuenta bancaria de Bruno por la suya?

Alicia no tiene medios para verificar si la cuenta bancaria es de Bruno o de Carlos. ¿Hay algo que podamos hacer para evitar que Carlos use esta estrategia para robar el dinero?

Si Bruno pudiera de alguna manera firmar la información, entonces Alicia podría verificar que la firma es válida y aceptar el mensaje. A su vez, si Carlos cambia la cuenta bancaria, entonces la firma ya no es válida, y Alicia rechazaría el mensaje. Esta es exactamente la funcionalidad que proporcionan las firmas digitales.

Lo que presentaremos ahora se llama Algoritmo de Firma Digital de Curva Elíptica, o ECDSA para abreviar. Este proceso es quizás un poco más complicado que la encriptación. Implicará algunas nuevas gimnasias matemáticas. Las definiremos a medida que sean necesarias. ¡Mantente despierto!

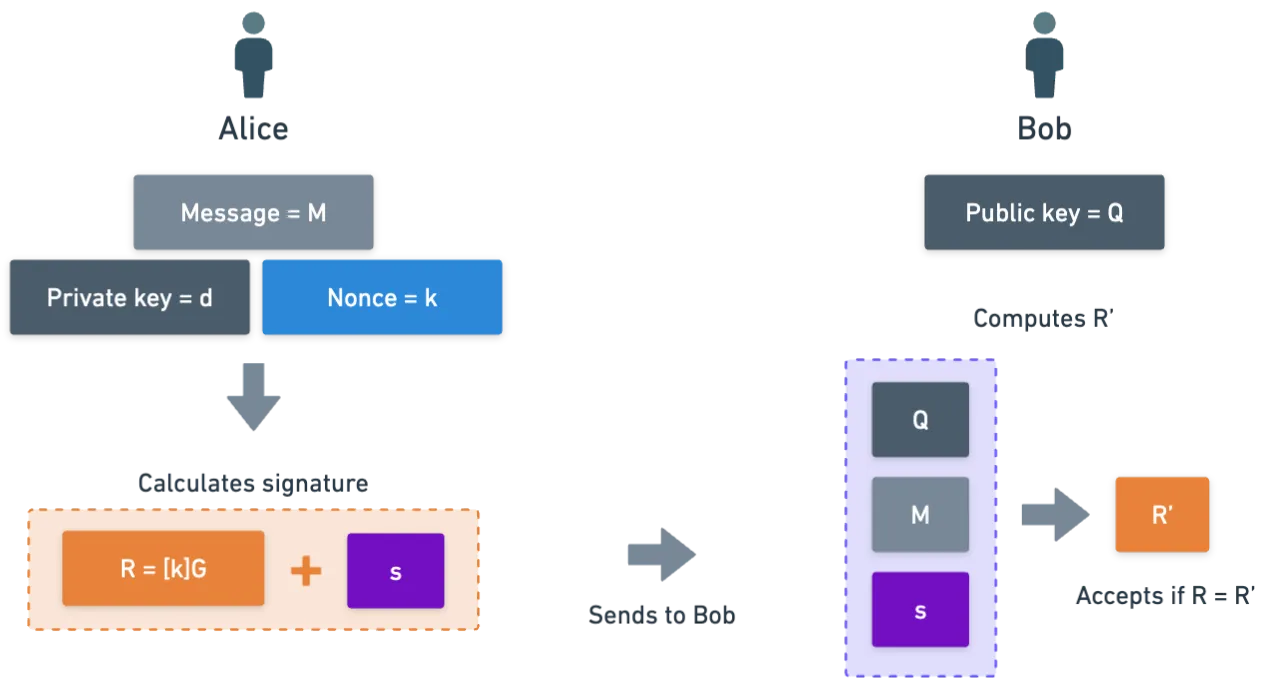
• Bruno codifica su mensaje, como lo hizo en el ejemplo de encriptación, pero esta vez la salida es un entero $M$. Veremos cómo hacer esto más adelante.
• Bruno luego elige un número aleatorio $k$, al igual que en el caso de la encriptación,
• También calcula $R = [k]G$. Denotaremos la coordenada x de $R$ con la letra $r$,
• El último cálculo que realiza es para el número $s$, calculado como:

$$s = k^{-1}(M + d.r) \ \textrm{mod} \ n$$

• Y finalmente, envía el par $(r, s)$ a Alicia.

El $k^{-1}$ en el cálculo de $s$ no es el recíproco de $k$ (es decir, no es $1/k$).

En cambio, $k^{-1}$ representa el inverso multiplicativo modular. Esencialmente, es un número que, cuando se multiplica por $k$, produce el siguiente resultado:

$$k.k^{-1} \ \textrm{mod} \ n = 1$$

Además, el módulo (n) es un número especial: es el orden del punto generador $G$. Cada punto en la curva elíptica tiene un orden, que es el entero más pequeño para el cual $[n]G = \mathcal{O}$. Este es también el orden del grupo $\mathbb{G}$.

Bien, eso fue mucho, pero tenemos nuestra firma. Todo lo que queda es verificarla. Como el mensaje es público, Bruno puede codificarlo al mismo número $M$ que usó Alicia. Y luego, sigue estos pasos:

• Calcula $w$ como el inverso modular de $s$, así que $w = s^{-1} \ \textrm{mod} \ n$.
• Bruno luego toma este valor y calcula $R' = [w.M]G + [w.r]Q$.
• Acepta la firma si la coordenada x de $R'$ coincide con el valor $r$.

Realizar los cálculos y verificar que $R' = R$ es un buen ejercicio para el lector. Si vas a intentarlo, recuerda que como $G$ es un generador de orden n, entonces $[n]G = \mathcal{O}$. También puedes necesitar usar algunas propiedades de aritmética modular.

Click to zoom

Y nuevamente, como por arte de magia, ¡una firma es realmente solo un par de números! La idea aquí es que calcular s es realmente fácil con el conocimiento de la clave privada, pero realmente difícil sin ella — ¡tendrías que resolver un problema DLP!

Si Carlos quiere cambiar el mensaje, no tiene otra opción que la fuerza bruta. Y sabemos cómo resulta eso para él (spoiler: no va a ser divertido).

Digamos esto de nuevo, para que quede claro:

Firmar implica calcular una especie de "desafío" $R$, y alguna "clave de verificación" $s$. El par $(R, s)$ constituye una firma.

El valor $s$ es especial porque, cuando se pone en una licuadora (es decir, algún proceso) junto con la clave pública $Q$ y el mensaje original $M$, produce de vuelta el desafío $R$. Y la idea es que $s$ solo puede calcularse con conocimiento de la clave privada.

Resumen

Hay varias técnicas y construcciones más que exploraremos en los próximos artículos, pero este es un buen lugar para detenernos por ahora.

Creo que no es tan importante entender cada pieza de matemática o cada cálculo en juego, sino apreciar cómo al final, tanto la encriptación como la firma digital realmente equivalen a un uso inteligente de operaciones de curva elíptica, aprovechando el poder del problema DLP.

La buena noticia es que hay mucho que podemos hacer con las herramientas que tenemos hasta ahora. Técnicas más sofisticadas requerirán la introducción de algunos conceptos nuevos y más complejos — y no iremos allí todavía.

Además, hay algunas cosas que aún no hemos explicado del todo, como cómo convertir un mensaje en un número, en el caso de firmas digitales, ni cómo obtener una máscara a partir de un punto en la curva elíptica, en el caso de encriptación.

¡Esto puede hacerse mediante hashing, una herramienta muy poderosa que será el tema central del próximo artículo!