Criptografía 101: Hashing

Este artículo forma parte de una serie más larga sobre criptografía. Si este es el primer artículo con el que te encuentras, te recomiendo comenzar desde el principio de la serie.

La última vez, analizamos un par de técnicas relacionadas con grupos de curvas elípticas, específicamente, firmas digitales y cifrado asimétrico.

Ambos métodos se basaban en la premisa de que el mensaje, o una máscara de mensaje, eran enteros. Pero, ¿cómo puede ser esto? Por ejemplo, es mucho más probable que un mensaje sea un texto secreto como "hola-mama-esto-es-un-mensaje-secreto", o más realistamente, algunos datos JSON como:

{
  "amount": 1000,
  "account": 8264124135836,
  "transactionReceiptNumber": 13527135
}

¡Estos claramente no son enteros! Por lo tanto, no son aptos para usarse "tal cual" de la manera que pretendíamos originalmente. Se requiere algún tipo de procesamiento.

A partir de ahora, nos desviaremos un poco de nuestro desarrollo de grupos y sus usos. Nos centraremos en otra herramienta que hará que nuestro arsenal criptográfico sea mucho más poderoso.

•••

Funciones de Hashing

En pocas palabras, una función de hashing o algoritmo toma algunos datos como entrada y produce información aparentemente aleatoria, como esta:

Representación de función de hashing como entrada de cualquier tipo, produciendo una salida binaria de longitud fija

La salida se suele llamar el hash de la entrada. Para nuestros propósitos, el algoritmo es como una caja negra, lo que significa que generalmente no nos interesa cómo se obtiene el hash. Lo que necesitas saber es que funciona esencialmente como una licuadora de datos: una vez que los datos entran, se mezclan por completo, y es imposible recuperar el contenido original.

Imagen de una licuadora — No estoy patrocinado por Bosch, por cierto. Espero no estar infringiendo ningún derecho de autor con esto...

De nuevo, no estamos tan interesados en cómo las funciones de hashing logran esto. Es mucho más importante entender qué propiedades tienen el algoritmo y el hash, y qué podemos hacer con ellos.

Bueno, a menos que estés tratando de desarrollar una nueva función de hashing, por supuesto. Si eso es lo que buscas, entonces OBVIAMENTE te importa el cómo. Aquí hay un documento del Instituto Nacional de Estándares y Tecnología (NIST) de EE. UU. con especificaciones para diferentes algoritmos de hashing; y aquí también hay una implementación de SHA-256 en Javascript, como referencia. Oh por Dios. Buena suerte con eso.

Para fines criptográficos, a menudo se requiere que las funciones de hashing tengan las siguientes características:

Salida determinista: Dada una entrada $A$ (como "Me encantan las tortasfritas"), se obtiene la misma salida cada vez que hasheamos $A$ .
Difusión: El más mínimo cambio en la entrada resulta en un cambio dramático en la salida. Por ejemplo, los hashes de "Me encantan las tortasfritas" y "Me encantan las portasfritas" son totalmente diferentes, irreconocibles entre sí.
No predictibilidad: El resultado de hashear algunos datos debe ser totalmente impredecible; no debe haber patrones reconocibles en el hash obtenido.
No reversibilidad: Reconstruir una entrada válida para un hash dado no debe ser posible, de modo que la única forma de afirmar que una entrada corresponde a un hash es mediante prueba y error (¡fuerza bruta!).
Resistencia a colisiones: Encontrar dos entradas que produzcan el mismo hash (o incluso hashes parcialmente coincidentes) debe ser realmente difícil.

No todos los algoritmos de hashing tienen todas estas propiedades. Por ejemplo, el algoritmo MD5 no proporciona resistencia a colisiones. Hace apenas unos días, me encontré con esta publicación que muestra una colisión de MD5 en dos cadenas que difieren en un solo bit.

Y dependiendo de nuestra aplicación del algoritmo, esto puede ser importante o no. Por ejemplo, MD5 se utiliza para verificar la integridad de archivos porque es rápido, y no nos preocupan tanto las colisiones en ese contexto.

La salida de las funciones de hashing tiene un tamaño fijo en la mayoría de los algoritmos. Y dado que todas las entradas son realmente solo bits de información, estamos esencialmente transformando una secuencia de bits de longitud arbitraria en una secuencia de bits de tamaño fijo aparentemente aleatoria. Esto se denota:

H: \{0,1\}^* \rightarrow \{0,1\}^n

Hay muchos algoritmos de hashing conocidos, como el mencionado MD5, las familias SHA-2 y SHA-3, el algoritmo de hashing de Ethereum Keccak256, Blake2, que se usa en Polkadot, y otros.

¿Para Qué Se Usan los Hashes?

Hay muchas aplicaciones para los hashes. Veremos que son útiles para construir protocolos criptográficos, pero hay otros escenarios donde el hashing resulta práctico. La lista a continuación es meramente ilustrativa; ten en cuenta que el hashing es una herramienta tremendamente poderosa con aplicación generalizada.

Verificaciones de integridad de datos: como se mencionó anteriormente, una función de hashing puede usarse para resumir un archivo grande en un pequeño fragmento de información. Incluso el más mínimo cambio en el archivo original hace que el hash cambie dramáticamente, por lo que puede usarse para verificar que un archivo no ha sido alterado.
Indexación basada en contenido: podemos generar un identificador para algún contenido, utilizando una función de hashing. Si la función es resistente a colisiones, entonces el identificador es muy probablemente único, y podría incluso usarse en aplicaciones de bases de datos como un índice.
Estructuras de datos basadas en hash: algunas estructuras de datos dependen del poder de los hashes. Por ejemplo, una lista hash puede usar el hash del elemento anterior como puntero, muy similar a lo que sucede en una Blockchain. Hay otras estructuras de datos importantes basadas en hash, como las tablas hash. Veremos una de estas estructuras más adelante en este artículo.
Esquemas de compromiso: algunas situaciones requieren que la información no se revele por adelantado. Imagina que quiero jugar piedra-papel-tijeras por correspondencia. Si envío "piedra" a mi oponente, pueden simplemente responder "papel" y ganar. Pero, ¿qué pasaría si enviamos un hash de "piedra" en su lugar? Exploraremos esto con más profundidad en el próximo artículo, pero las funciones hash son útiles en estas situaciones.

Muy bien, ahora sabemos qué son las funciones de hashing, y hemos cubierto algunas de sus aplicaciones. Volvamos a la criptografía basada en grupos y discutamos la importancia de los hashes en ese contexto.

•••

Los Hashes al Rescate

Al principio de este artículo, notamos que tanto el cifrado como la firma requieren algún tipo de procesamiento. En el cifrado, necesitábamos procesar una máscara, y en la firma digital, un mensaje. Y en ambos escenarios, necesitábamos que la salida fuera algún valor entero. ¿Pueden las funciones de hashing ayudarnos en este esfuerzo?

Recuerda que una función de hashing producirá una secuencia de bits de tamaño fijo... ¿Y qué es eso, si no una representación binaria de un entero?

(10010100010111100)_2 = (75964)_{10}

El mismo número, expresado en diferentes bases.

Así de simple, el hashing proporciona una solución a nuestro problema: todo lo que necesitamos es ejecutar nuestro mensaje $M$ a través de una función de hashing adecuada. La salida, $H(M)$ , será un número, justo lo que necesitábamos. Increíble. Las cosas están empezando a encajar.

Obteniendo Puntos de Curvas Elípticas

Al ejecutar una función de hashing, la salida será en general un número binario; otra forma de expresarlo es decir que hasheamos hacia un número entero. Sin embargo, hay situaciones en las que esto no es suficiente: podemos requerir hashear hacia un punto en una curva elíptica. De hecho, se nos requerirá hacer esto en el próximo artículo.

Una posible manera de hashear hacia una curva elíptica es calcular $h = H(M)$ normalmente, y computar un punto $[h]G$ como nuestra salida, siendo $G$ un generador de la curva elíptica. Existen métodos más sofisticados, pero no profundizaremos en más detalles. El punto es que podemos expandir la definición de lo que es una función hash, permitiendo hashear hacia algún conjunto arbitrario $A$ , como esto:

H: \{0,1\}^* \rightarrow A

De nuevo, la forma en que esto se logra es irrelevante para nosotros, y estamos principalmente preocupados por qué propiedades tiene el algoritmo: ¿es resistente a colisiones? ¿Es irreversible?

•••

El Eslabón Más Débil

Volvamos al esquema de firma digital (ECDSA) del artículo anterior. Ahora sabemos que el mensaje M puede procesarse en un número mediante el uso de una función hash, $H(M)$ .

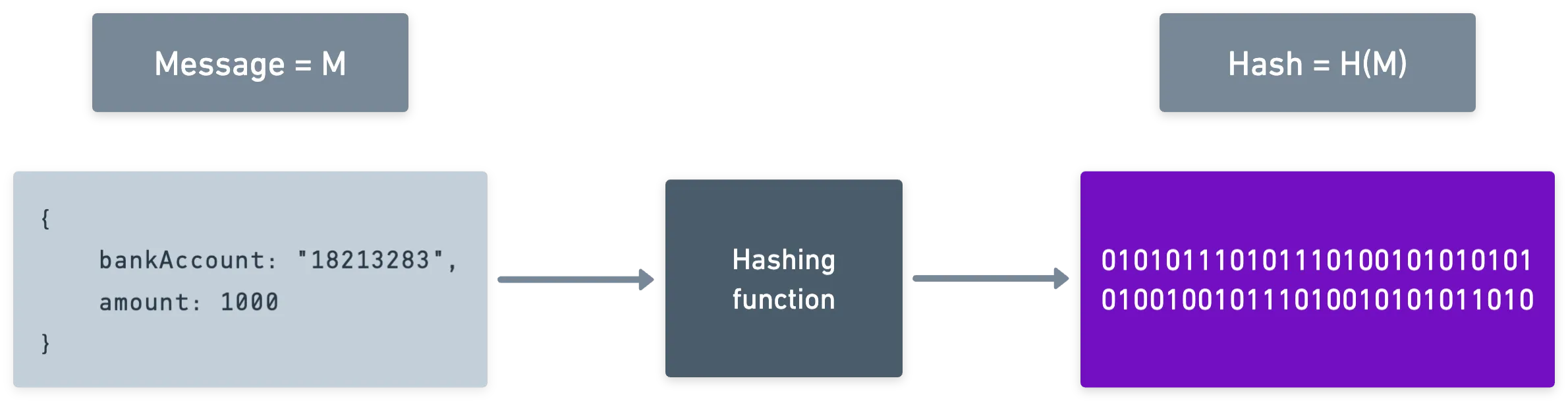
Otra visualización de función de hashing

También dijimos que la seguridad de la firma digital radica en lo difícil que es calcular la "clave" de validación $s$ . Pero el hashing introduce un nuevo problema. Y lo explicaremos mediante un ejemplo.

Charlie quiere manipular el mensaje original $M$ . Evidentemente, cambiar el mensaje cambiará el hash $H(M)$ , y esto invalida la firma.

Sin embargo, si $H$ resulta ser una función de hashing donde es fácil encontrar colisiones, entonces Charlie podría producir un nuevo mensaje $M'$ cambiando la cuenta bancaria a la suya, y luego jugar con la cantidad hasta que el hash del nuevo mensaje coincida con el original, $H(M') = H(M)$ .

¡Y boom! Así de fácil, Charlie ha burlado nuestra seguridad. En esta aplicación particular, una función de hashing no resistente a colisiones rompería el algoritmo por completo.

En primer lugar, este es un claro ejemplo de que no todas las funciones de hashing son adecuadas para cada aplicación. Y en segundo lugar, la seguridad de cualquier esquema o protocolo que podamos imaginar estará limitada por su parte más débil. Hay un sabio proverbio que dice "una cadena no es más fuerte que su eslabón más débil". Y eso ciertamente se aplica aquí.

Así que sí, es importante tener estas cosas en mente al diseñar técnicas criptográficas. Siempre debes analizar la seguridad de cada componente de tu protocolo, y no solo centrarte en un aspecto del mismo.

Si quieres más información sobre temas relacionados con la seguridad, intenta leer este apartado en la serie.

•••

Árboles de Merkle

Antes de terminar, quiero hablar sobre una importante estructura de datos basada en hash, que es esencial en el desarrollo de Blockchain: los árboles de Merkle.

En esencia, es solo una estructura de árbol donde la información contenida en cada nodo es simplemente el hash de los nodos hijos. Así:

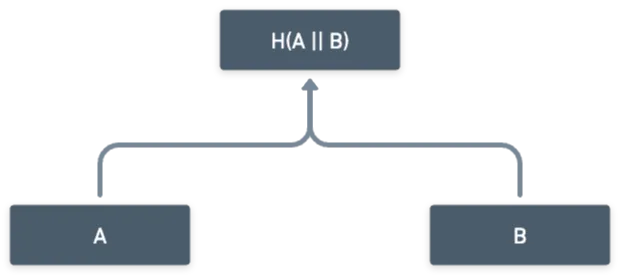
Construcción de nodos en árboles de Merkle — Un nodo de un árbol de Merkle

Repitiendo este patrón se llegará a una estructura de árbol:

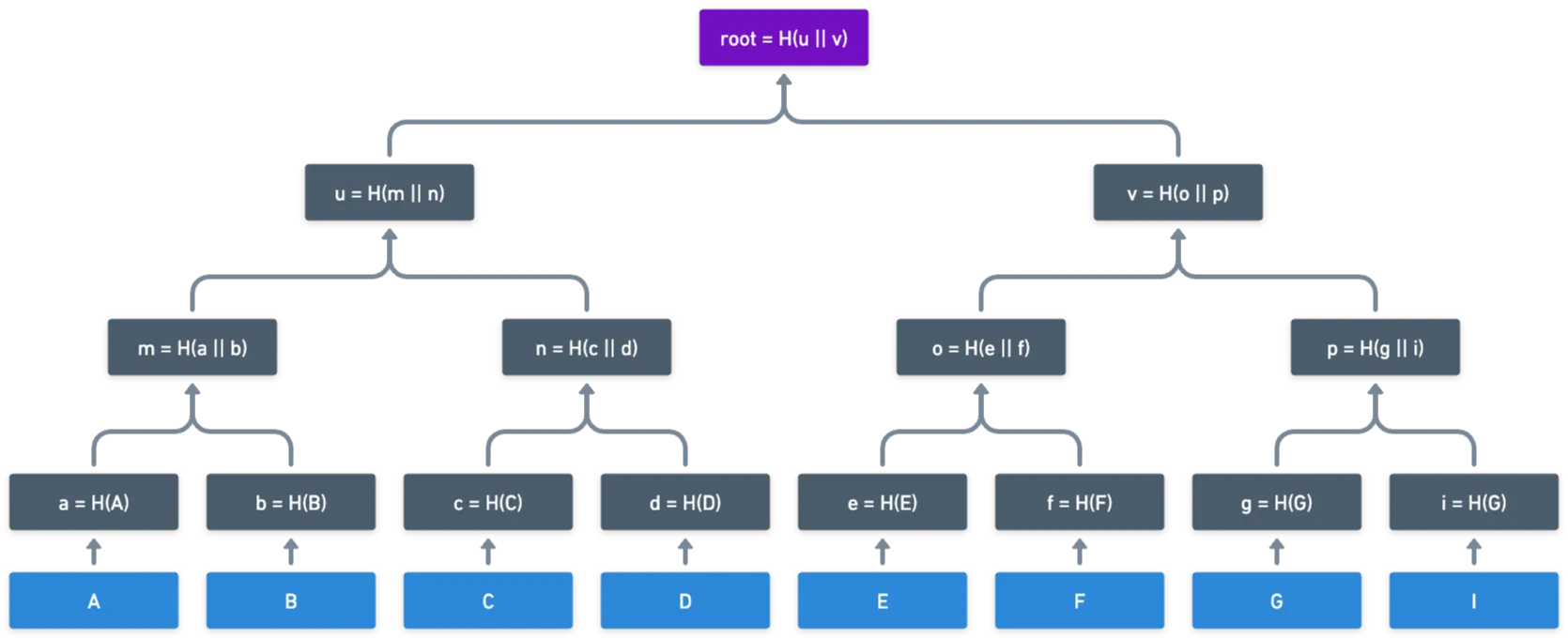
Todo lo que esto hace es reducir (posiblemente) mucha información a un solo hash, que es la raíz del árbol. Pero espera, ¿no hace una función hash lo mismo? Si simplemente hasheamos:

h = H(A || B || C || D || E || F || G || I)

También obtenemos un único hash asociado con la misma información. Cambiar un solo bit en cualquiera de las entradas originales causa cambios dramáticos en el hash producido. Entonces... ¿Por qué molestarse en crear una estructura de árbol extraña?

Por cierto, el operador $||$ significa concatenación de bits. Es simplemente pegar los bits de las entradas juntos. Por ejemplo, si $A = 0101$ y $B = 1100$ , entonces $A || B = 01011100$ .

Resulta que usar un árbol desbloquea nuevos superpoderes. Imagina esta situación: alguien (digamos Andrés) afirma que $h$ corresponde a la entrada $A$ , pero no quiere revelar las otras entradas $(B, C, D...)$ . ¿Cómo podemos comprobar si $A$ produce efectivamente $h$ ?

Nuestra única opción es hashear toda la entrada y comparar con $h$ . Y, por supuesto, para esto, necesitamos todas las entradas originales utilizadas por Andrés. Pero él no quiere compartir todas las entradas, y enviar un camión lleno de información (posiblemente miles de valores) a través de una red no suena muy tentador...

La Solución del Árbol de Merkle

La estrategia claramente se vuelve ineficiente. Los árboles de Merkle permiten una solución más elegante. Imagina que Andrés ha producido en cambio una raíz de Merkle $R$ de todas sus entradas $(A, B, C...)$ :

R = \textrm{Merkle}(A, B, C...)

Él afirma que $A$ está en el árbol. ¿Cómo puede probar esto? Y aquí es donde ocurre la magia: puede enviar unos pocos nodos del árbol como prueba, y podemos verificar que $R$ se produce efectivamente con $A$ . Mira esta imagen:

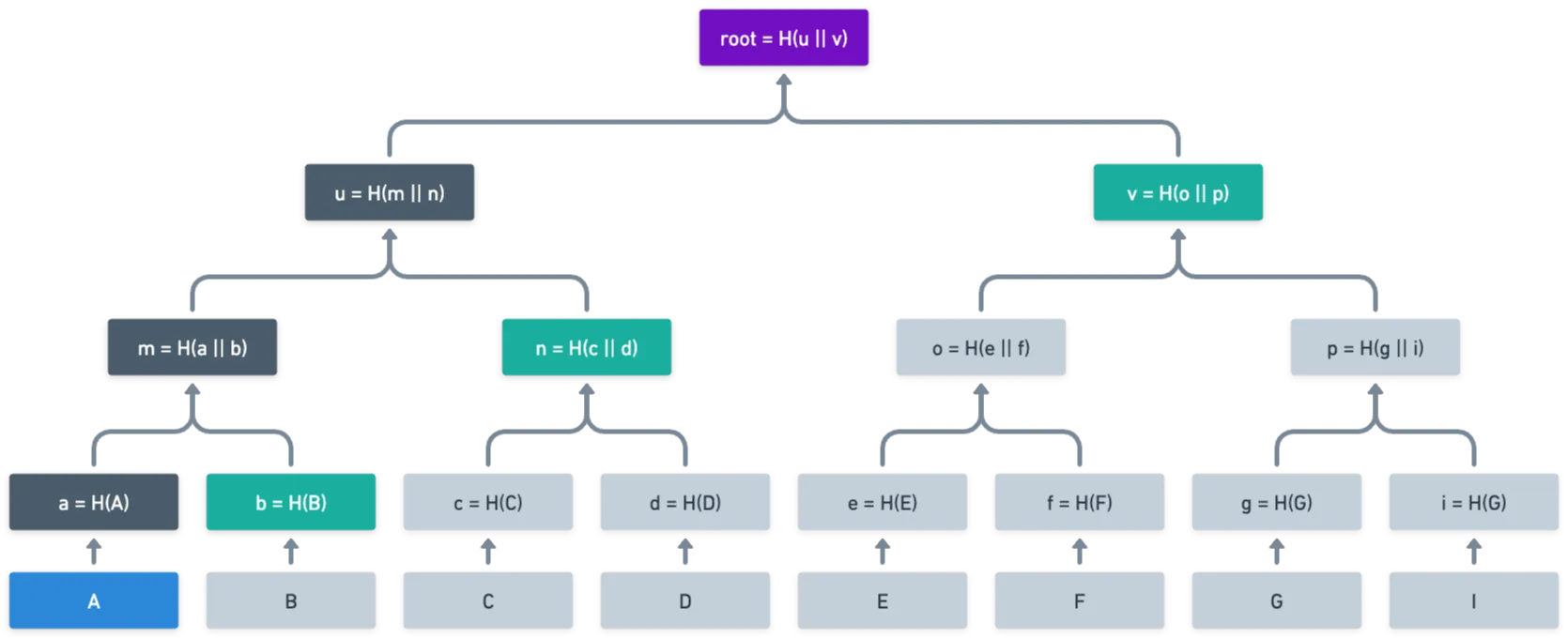
Visualización de prueba de Merkle, con solo unos pocos nodos necesarios para la prueba

¿Ves los nodos resaltados en verde? Esa es toda la información que realmente necesitamos para calcular la raíz. Mira, podemos calcular $m = H(a || b)$ , y luego $u = H(m || n)$ , y finalmente $H(u || v)$ , y listo. En lugar de revelar todas las hojas del árbol $(A, B, C, D, E, F, G, I)$ , podemos demostrar que $A$ pertenece al árbol revelando ¡solo tres nodos!

Este sistema se conoce como prueba de Merkle. Y algo muy interesante al respecto es lo bien que escala. Resulta que el número de nodos $N$ que tenemos que revelar escala logarítmicamente con el número de entradas:

N = \textrm{log}_2(\#\textrm{inputs})

Así que para 1024 entradas, solo tenemos que revelar 10 nodos. Para 32768, 15 nodos serán suficientes.

Una imagen de una foca feliz — Relajante

Los árboles de Merkle son una de las estructuras de datos criptográficas más utilizadas, potenciando Blockchains en todas partes. Hay investigación activa en curso para posiblemente reemplazarlos con un nuevo chico en el bloque, llamado árbol de Verkle, pero la idea es generalmente la misma: probar que algo pertenece a un conjunto de datos, sin revelar el conjunto de datos completo.

¡Esto solo demuestra cómo los hashes pueden utilizarse de maneras inteligentes para lograr algunas hazañas bastante mágicas!

•••

Resumen

Lentos pero seguros, estamos construyendo un sólido conjunto de herramientas criptográficas. Ahora tenemos el hashing a nuestra disposición, junto con los grupos, la aritmética modular, y las curvas elípticas. ¡Genial!

Después de este breve desvío de nuestro desarrollo en curvas elípticas, volveremos a la acción en el próximo artículo, y exploraremos qué más podemos hacer con nuestro conocimiento actual.