arkanaCriptografía 101 (Anexo): Evaluando la Seguridad
Este artículo forma parte de una serie más larga sobre criptografía. Si este es el primer artículo con el que te encuentras, te recomiendo comenzar desde el principio de la serie.
A lo largo de nuestro viaje, nuestro objetivo siempre ha sido tratar de entender los fundamentos matemáticos que sostienen la criptografía moderna. Es una tarea importante en sí misma — la criptografía consiste en crear acertijos realmente difíciles, después de todo. No hay creación si no podemos entender las herramientas involucradas.
Y aunque todavía hay mucho por explorar en cuanto al diseño de protocolos criptográficos, creo que ahora es un buen momento para tomar otro pequeño desvío y cambiar nuestro enfoque hacia un aspecto que aún no hemos discutido. Intentemos responder las siguientes preguntas:
¿Qué tan seguros son los métodos que hemos aprendido hasta ahora?
¿Qué entendemos por seguridad?
¿Cómo se mide?
La mejor manera de responder a esto, en mi humilde opinión, es hacer un viaje rápido a través de la historia de la criptografía. Al hacer esto, nos encontraremos con algunos problemas que pueden poner en peligro la utilidad de nuestros métodos desde el principio, mientras que otros se volverán más claros lentamente.
Y para empezar, volvamos al principio.
El Cifrado César
La idea de proteger datos en las comunicaciones ciertamente no es nueva.
Existen registros de intentos de ocultar mensajes secretos en civilizaciones antiguas. Un ejemplo famoso, y uno de los primeros usos registrados de técnicas criptográficas, es el cifrado César, que data del año 100 a.C. Es una técnica muy simple: cada letra del alfabeto se desplaza un número determinado de posiciones. Por lo tanto, se categoriza como un cifrado por sustitución, porque cada letra se sustituye por otra, siguiendo un conjunto específico de reglas.
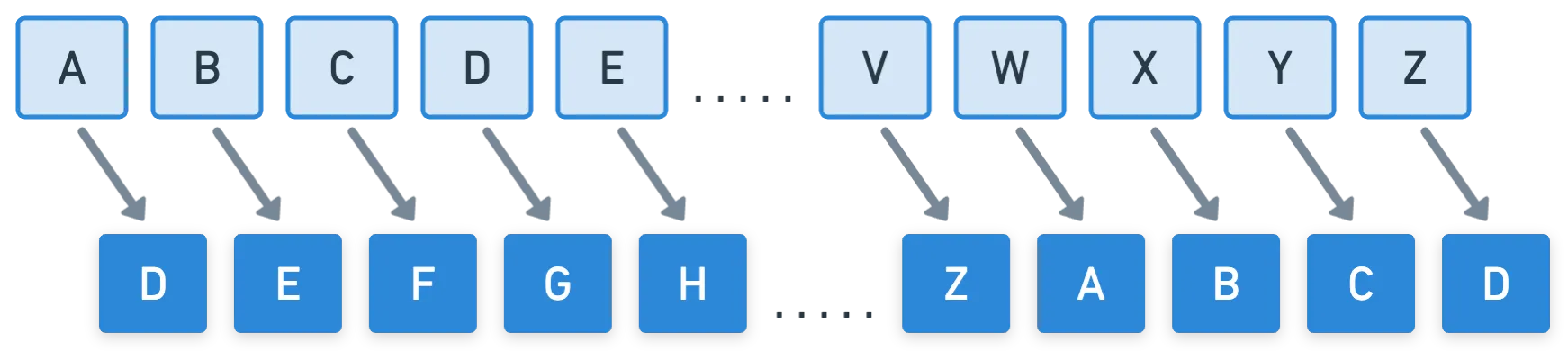
Siempre que sepas cuántas posiciones se desplazan los caracteres, entonces puedes descifrar mensajes cifrados con esta técnica. Por ejemplo, si el desplazamiento fue de letras (como en la imagen de arriba), entonces el texto cifrado "khooraruog" puede mapearse de vuelta al texto original "helloworld". Por supuesto, podríamos agregar caracteres especiales, pero mantengámonos en el método original y simple.
Todo iba bien hasta que un tipo llamado Al-Kindi llegó y descifró el código, explotando una falla fatal. ¿Puedes adivinar cuál es?
Para ser justos, pasaron casi mil años antes de que alguien propusiera esta explotación, ¡así que no te preocupes demasiado si no la detectaste!
La Explotación
En cualquier idioma, algunas letras aparecen con mayor frecuencia que otras. Si analizamos esas frecuencias en una gran cantidad de texto, emergerá una distribución. Para el inglés, esa distribución se ve aproximadamente así:
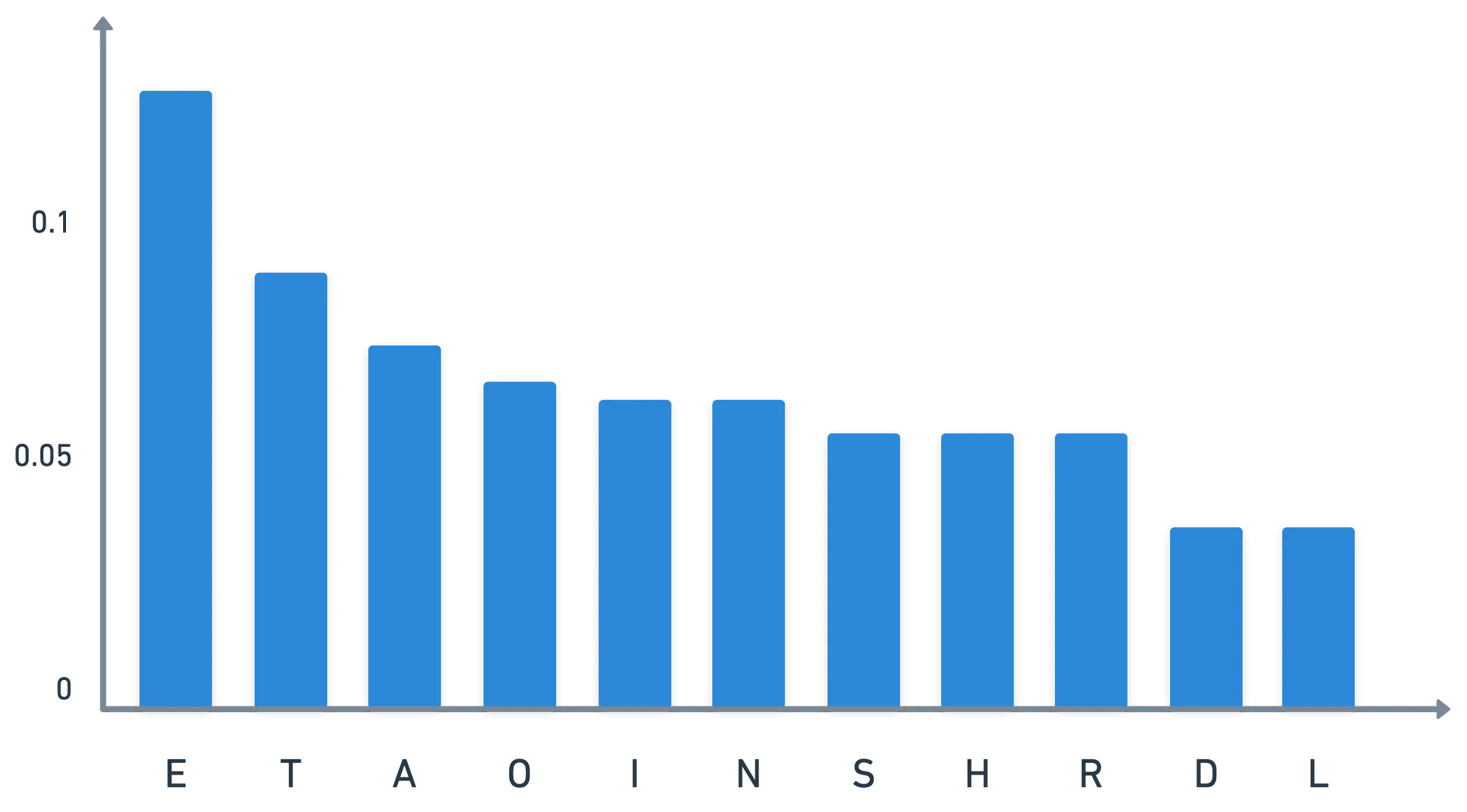
¿Qué podemos hacer con esta información, te preguntas? Bueno, si el mensaje resulta ser algún texto en inglés, entonces podemos verificar las frecuencias de las letras en nuestro mensaje cifrado. ¡Y es probable que la letra que aparece con más frecuencia sea la versión cifrada de la letra !
Pensemos en esto por un minuto: por ejemplo, si la letra se cifra como la letra , entonces es probable que aparezca con frecuencia. Y las probabilidades de que esto suceda aumentan a medida que el texto se alarga, porque las letras comienzan a repetirse.
Esto se llama análisis de frecuencia. Y el problema realmente se reduce a tener una distribución no uniforme asociada con nuestro texto cifrado.
No recuerdo si he mencionado esto antes, pero texto cifrado (ciphertext) es una forma en que llamamos a la salida de un proceso de cifrado, y la entrada a menudo se llama texto plano (plaintext).
En consecuencia, esto significa que podemos inferir cierta información solo mirando los datos cifrados. Y eso es algo que nunca deberíamos poder hacer. En el caso de un método de sustitución "ideal", esto significaría que cada carácter es igualmente probable que aparezca en el texto cifrado, lo cual no es el caso en el cifrado César.
En resumen, la gran idea aquí es la siguiente:
No deberíamos poder aprender nada de los datos cifrados mirando el texto cifrado.
Y esta es una de las grandes razones por las que la mayoría de las técnicas que hemos visto hasta ahora introducen algún tipo de aleatoriedad en la mezcla: para hacer que las cosas sean indistinguibles de datos aleatorios. Esto significa que las posibilidades de que aparezca cualquier caracter en el texto cifrado son casi las mismas, es decir, en términos probabilísticos, que la distribución de caracteres es (casi) uniforme:
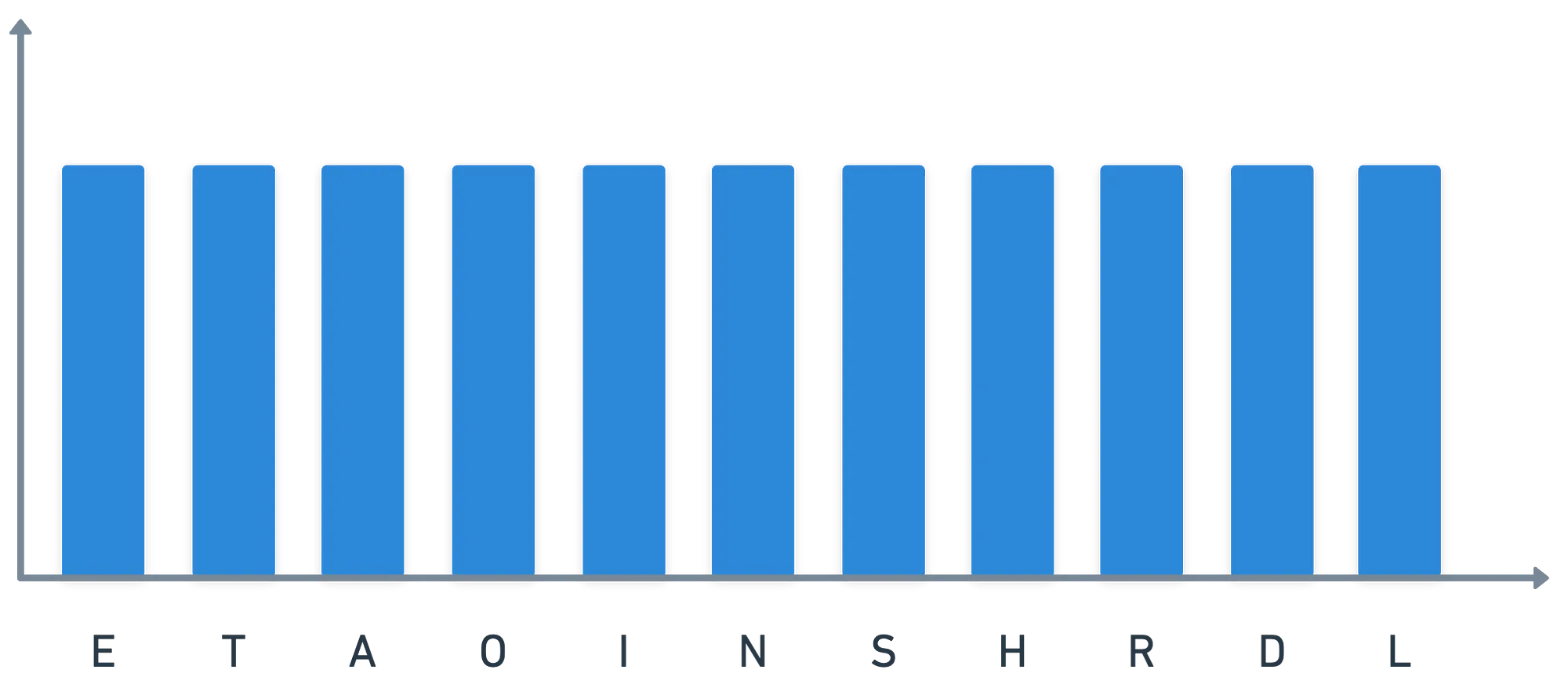
Garantizado: si no se cumple esta condición, entonces es muy probable que un método no sea seguro, ya que esto abre la puerta para análisis basados en la distribución del texto cifrado. Nos hemos topado con un requisito de seguridad al diseñar métodos criptográficos.
Tamaños de Clave
La seguridad está en parte relacionada con la ausencia de estas puertas traseras o vectores de ataque que pueden comprometer nuestros esfuerzos para proteger datos, como el ejemplo presentado anteriormente. Por supuesto, existen otros tipos de ataques, como ataques de texto plano elegido, ataques de canal lateral, entre otros.
Y es muy importante escrutar cuidadosamente cada aspecto de nuestros métodos, ya que incluso la más mínima vulnerabilidad puede romper todo el sistema. Como mencioné en el artículo sobre hashing, y repito ahora:
Una cadena es tan fuerte como su eslabón más débil
Aun así, supongamos que hemos hecho nuestra tarea y estamos bastante seguros de que nuestra técnica es muy sólida y no tiene puertas traseras obvias. ¿De qué más deberíamos preocuparnos?
Fuerza bruta, ¡eso es!
La pregunta es simple: ¿qué tan fácil sería romper un método criptográfico solo por prueba y error? Hablé brevemente sobre esto en un artículo anterior, pero ahora tratemos de cuantificar esta tarea.
En términos generales, hay dos ingredientes esenciales para este asunto:
- El tamaño de la estructura matemática subyacente
- La complejidad computacional de las operaciones involucradas en nuestro problema
Por ejemplo, en la Criptografía de Curva Elíptica (ECC), esto significa que nos preocupamos por qué tan grande es el grupo de curva elíptica, y también nos preocupamos por cuánto esfuerzo computacional se requiere para probar valores uno por uno.
Tamaños de Clave RSA
En lugar de centrarnos en ECC, comencemos analizando RSA. Repaso rápido: RSA se basa en el hecho de que es difícil encontrar los dos factores primos de un número dado .
Comencemos con algo pequeño. Digamos que y tienen como máximo byte ( bits) de longitud. Esto significa que tiene como máximo bytes de longitud. ¿Qué tan difícil sería encontrar sus factores primos?
Por supuesto, esto sería realmente fácil. Puedes probarlo tú mismo con un script rápido. Para que esto sea difícil — y por lo tanto útil para la criptografía —, necesitamos que y sean mucho más grandes. Y a medida que usamos números más grandes, la factorización se vuelve exponencialmente más difícil.
En los primeros días de RSA, se creía que usar claves ( y ) que tuvieran como máximo bits de longitud haría que el esquema de cifrado fuera seguro. Pero el poder computacional solo ha aumentado en las últimas décadas, haciendo posible resolver el problema de factorización para claves de 512 bits en cuestión de días o incluso horas. Eso no suena muy seguro...
¿Qué hacer entonces? Bueno, aumentar los tamaños de clave, ¡por supuesto! Y así, hoy en día la recomendación es usar claves de 2048 bits. Se piensa que con la potencia de cálculo disponible actualmente, todavía tomaría un tiempo monstruosamente largo resolver el problema de factorización con estos tamaños de clave. Pero eso podría cambiar en el futuro, a medida que las computadoras se vuelvan más potentes.
La computación cuántica parece estar a la vuelta de la esquina... Así que quién sabe.
Tamaños de Clave ECC
En comparación, veamos qué sucede cuando trabajamos con curvas elípticas. Mencionamos cómo multiplicar un punto por algún número involucraba algunos pasos. Y eso es muy importante, porque el algoritmo de doble y suma debe ejecutarse cada vez que probamos un número para verificar que resuelve el problema del logaritmo discreto:
Es decir, la fuerza bruta es mucho más costosa computacionalmente que simplemente multiplicar dos números, como es el caso de RSA — nuestra estructura subyacente es más compleja. Y a su vez, esto significa que podemos lograr el mismo nivel de seguridad con tamaños de clave más pequeños. Por ejemplo, una clave de 256 bits en ECC es aproximadamente equivalente en seguridad a una clave de 3072 bits en RSA.
¿Importa el Tamaño de la Clave?
¡Ah, gran pregunta! Hay un par de cosas a considerar aquí.
En general, cuanto más grandes sean tus claves, más costosos se vuelven tus cálculos. No es lo mismo calcular y , ¿verdad? Y así, si bien sabemos que aumentar el tamaño de la clave es bueno para la seguridad, definitivamente no es bueno para la velocidad. Por lo tanto, tamaños de clave más grandes no siempre son mejores.
Elegir el tamaño de clave correcto es realmente un acto de equilibrio. Depende de lo que valoremos más: velocidad, seguridad, o un punto medio entre ambos.
Si no nos importa demasiado la velocidad y necesitamos que nuestros métodos sean muy seguros, entonces se requieren claves más grandes. Pero podemos requerir algoritmos más rápidos, y así reducir los tamaños de clave puede ser una opción.
Resumen
Este breve artículo recorre rápidamente algunos de los aspectos más importantes relacionados con la seguridad. En realidad, este tipo de análisis pertenece a una rama completa por sí misma: el criptoanálisis, que es una especie de hermano de la criptografía. Sería casi de mal gusto que dijera que este es un artículo de criptoanálisis; más bien, es una introducción muy suave a algunas de las ideas detrás de la disciplina.
Sin embargo, una cosa está clara: diseñar métodos criptográficos es tan importante como entender cómo romperlos. Omitir este análisis nos deja en riesgo de crear un sistema defectuoso, que en última instancia no cubre las garantías de seguridad que podríamos estar ofreciendo a nuestros clientes, y eso no es bueno.
Intencionalmente omití introducir la idea de un parámetro de seguridad, solo para mantener las cosas simples. Es posible que veas esto en artículos o discusiones técnicas, por lo que quizás quieras leer al respecto como una generalización de algunos de los conceptos discutidos anteriormente.
Con esto, al menos tenemos una idea general de algunas posibles debilidades en nuestros métodos, aunque hay mucho más que cubrir en esta área. ¡Solo ten siempre en cuenta que la seguridad no está asociada con cuán elegantes son las matemáticas. Elegancia no equivale a seguridad, ¡y un análisis cuidadoso siempre es una buena práctica!