Criptografía 101: Firmas Recargadas

Este artículo forma parte de una serie más larga sobre criptografía. Si este es el primer artículo con el que te encuentras, te recomiendo comenzar desde el principio de la serie.

Si has estado siguiendo la serie, entonces ya has visto una buena cantidad de locuras criptográficas. Especialmente en el artículo anterior. Aun así... Eso es solo la punta del iceberg.

Hay mucho más por aprender. Podemos hacer muchas más cosas con curvas elípticas (y grupos en general, para ser justos). En particular, las firmas digitales tienen algunas variantes elegantes que resultan extremadamente útiles en el contexto adecuado. Este será el tema del artículo de hoy.

Una Advertencia Amistosa

Creo que es en este punto de la serie donde las matemáticas se vuelven un poco más picantes de lo habitual. La complejidad de los protocolos que se presentarán es un poco mayor. Si estás aquí solo para tener una idea general de las técnicas criptográficas, entonces te sugiero leer solo la introducción de cada tema. Haré mi mejor esfuerzo para mantener las introducciones simples y autónomas, de modo que proporcionen una buena idea general, sin la molestia de entender las matemáticas.

¡Vamos a ello!

Firmas Ciegas

En algunos casos, puede ser necesario firmar información privada. Por ejemplo, en un sistema de votación, un usuario puede querer mantener su voto privado, pero requerir el respaldo de algún tercero. Este último tendría que firmar el voto a ciegas — sin saber cuál es el voto del usuario.

Por supuesto, aunque esto es técnicamente posible, la firma ciega debe implementarse con cuidado. No querrás estar firmando a ciegas una transacción que vacíe tu cuenta bancaria, después de todo.

Aun así, si se necesitan firmas ciegas, hay muchas formas de construirlas. Una posibilidad es adaptar esquemas de firma existentes. En particular, adaptar las firmas de Schnorr es bastante simple. ¡Intentémoslo!

El punto es que Alicia no sabe lo que está firmando — Bruno le pedirá que firme algún mensaje $M$ que él previamente ciega o enmascara. Y después de elaborar la firma, Bruno tiene una forma de desenmascararlo, para que la verificación funcione con su mensaje original.

Click to zoom

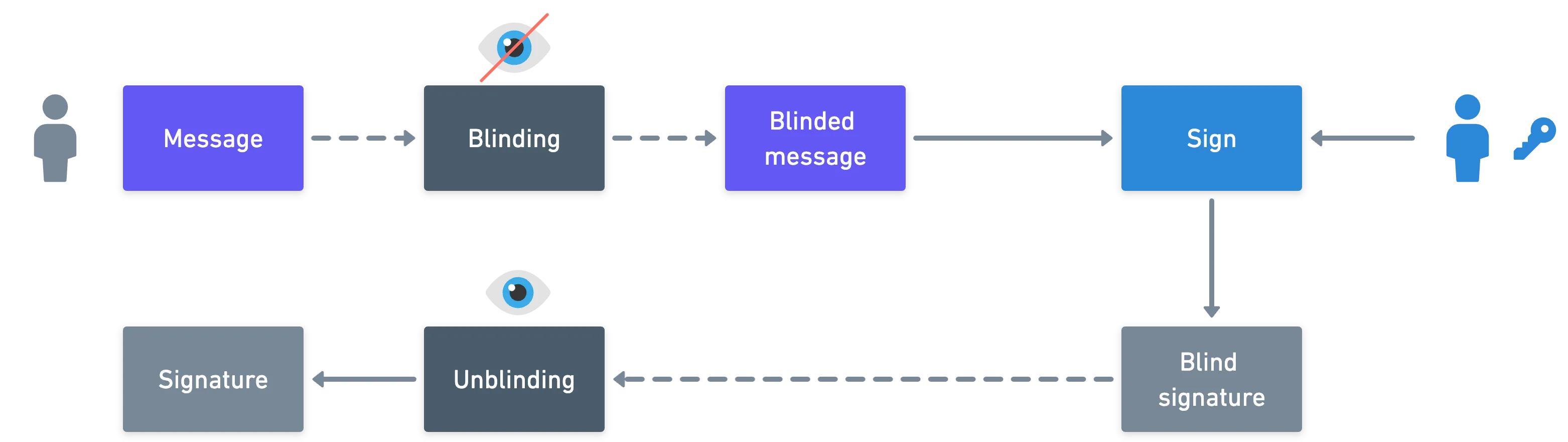
En resumen:

Las firmas ciegas permiten firmar información privada

El Protocolo

Comenzamos como de costumbre: Alicia tiene una clave privada $d$ y una clave pública $Q = [d]G$. Ella será nuestra firmante. Como siempre, $G$ es un generador para el grupo de curva elíptica elegido, y tiene orden $n$.

El proceso comienza con Alicia eligiendo un entero aleatorio $k$, y calculando $R = [k]G$. Ella envía esto a Bruno, y entonces él comienza el procedimiento de cegado:

• Bruno elige un entero aleatorio $b$, que se llama el factor de cegado,
• Luego calcula:

$$R' = R + [b]Q$$

• Y usa esto para calcular un desafío:

$$e' = H(M || R')$$

• Finalmente, también ciega el desafío:

$$e = e' + b \ \textrm{mod} \ n$$

Todo lo que queda es que Alicia firme. Ella recibe $e$, y simplemente calcula la firma como de costumbre:

$$s = k + e.d \ \textrm{mod} \ n$$

En este ejemplo particular, Bruno no tiene que hacer nada al recibir la firma — la salida es simplemente $(s, e')$. Pero en general, es posible que necesite revertir el proceso de cegado en otras versiones de firmas ciegas.

La verificación ocurre exactamente como en el caso estándar de firma de Schnorr:

$$V = [s]G - [e']Q$$

Si esto resulta ser igual a $R'$, entonces $H(M || V)$ será exactamente igual al desafío $e'$, y la firma es aceptada. Y este debería ser el caso, porque:

$$V = [e.d + k]G - [e'.d]G = [(e' + b)d - e'.d + k]G$$ $$= [e'.d - e'.d + k + b.d]G = [k]G + [d.b]G = [k]G + [b]Q = R'$$

Como un reloj, vemos que un $s$ correctamente calculado debería de hecho verificar la firma (porque recuperamos el desafío original).

Vale aclarar que estoy omitiendo intencionalmente las operaciones módulo $n$, por simplicidad. Pero para un tratamiento riguroso, deberían incluirse en la demostración.

Firmas ciegas, listo. No es tan loco, cierto?

Ahora que ya hemos calentado, subamos el nivel...

Firmas de Anillo

Cada vez que firmas digitalmente algo, la verificación ocurre con conocimiento de tu clave pública. Por lo tanto, no tienes anonimato: tu clave pública te identifica como un individuo que posee una clave privada. Pero, ¿y si te digo que hay una manera de firmar cosas anónimamente?

Las firmas de anillo ofrecen tal funcionalidad. La premisa es que una sola persona en un grupo de personas genera una firma que no revela quién en el grupo fue el firmante original. Algo como esto:

Click to zoom

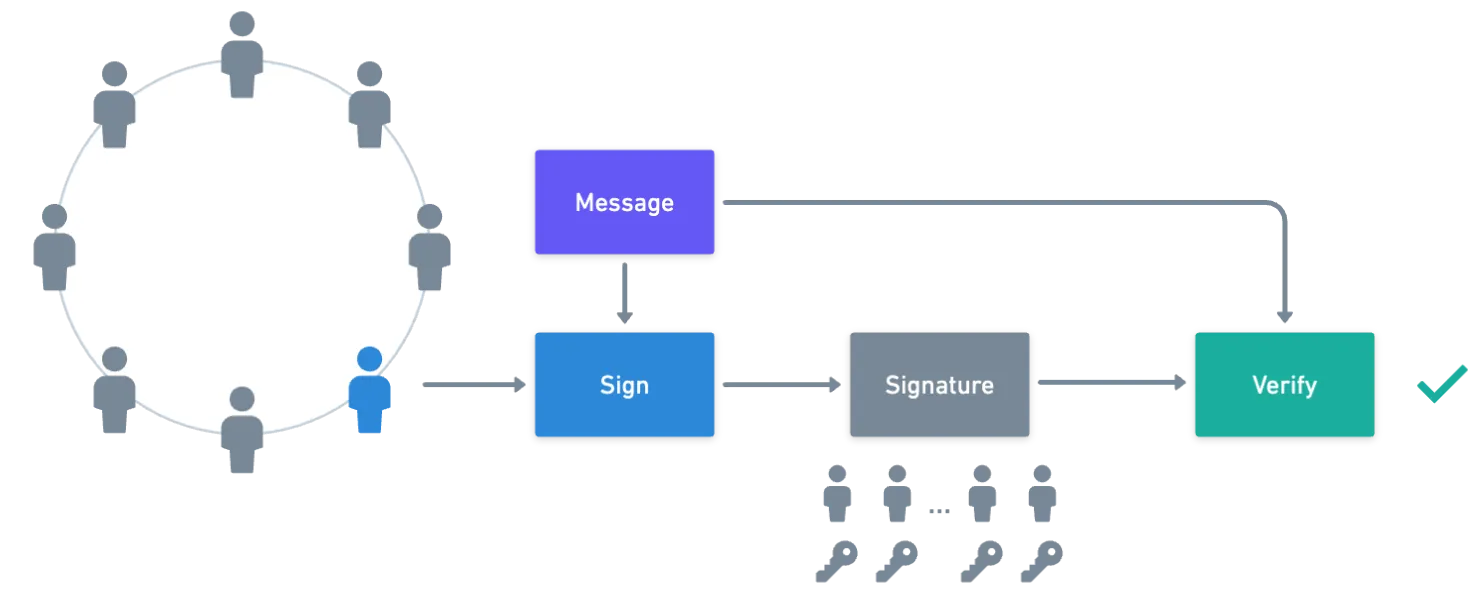
De nuevo, como un breve resumen preliminar:

Las firmas en anillo permiten a un usuario en un grupo crear una firma que podría haber sido producida por cualquier miembro del grupo, preservando así el anonimato del usuario

Creando el Anillo

Para lograr este comportamiento de anonimato, primero debemos forjar una estructura nueva y ligeramente inusual, llamada anillo.

El concepto de un anillo es el de un conjunto ordenado (en este caso, de participantes), cuyo orden determina una serie de cálculos que comienzan desde un valor $A$, y terminan en el mismo valor $A$. Y como siempre, la idea es que elaborar dicha secuencia de cálculos solo es factible con el conocimiento de una clave privada.

Por cierto, esto no es un anillo como en la estructura algebraica abstracta. Hablaremos de esos más adelante.

Entonces, para la configuración: el anillo tiene $p$ participantes, que como se mencionó anteriormente, están ordenados. Es decir, Alicia es la participante $\#1$, Bruno es el participante $\#2$, y así sucesivamente.

Sara, que es la participante $s^{th}$, tiene conocimiento de las claves públicas de todos los demás participantes — denotaremos esas como $Q_i$. También tiene su propio par de claves privada y pública, que van a ser $d_s$ y $Q_s = [d_s]G$.

Para producir una firma para un mensaje $M$, Sara hace lo siguiente:

• Elige un entero aleatorio $k$, y calcula $R = [k]G$.
• Luego calcula una semilla, $v = H(M || R)$.

Esta semilla se utilizará para un proceso iterativo. Comienza estableciendo $e_{s+1} = v$, y luego para cada otro de los $p$ participantes en el anillo:

• Elige un valor aleatorio $k_i$, y calcula:

$$R_i = [k_i]G + [e_i]Q$$

• Y calcula el siguiente desafío:

$$e_{i+1} = H(M || R_i)$$

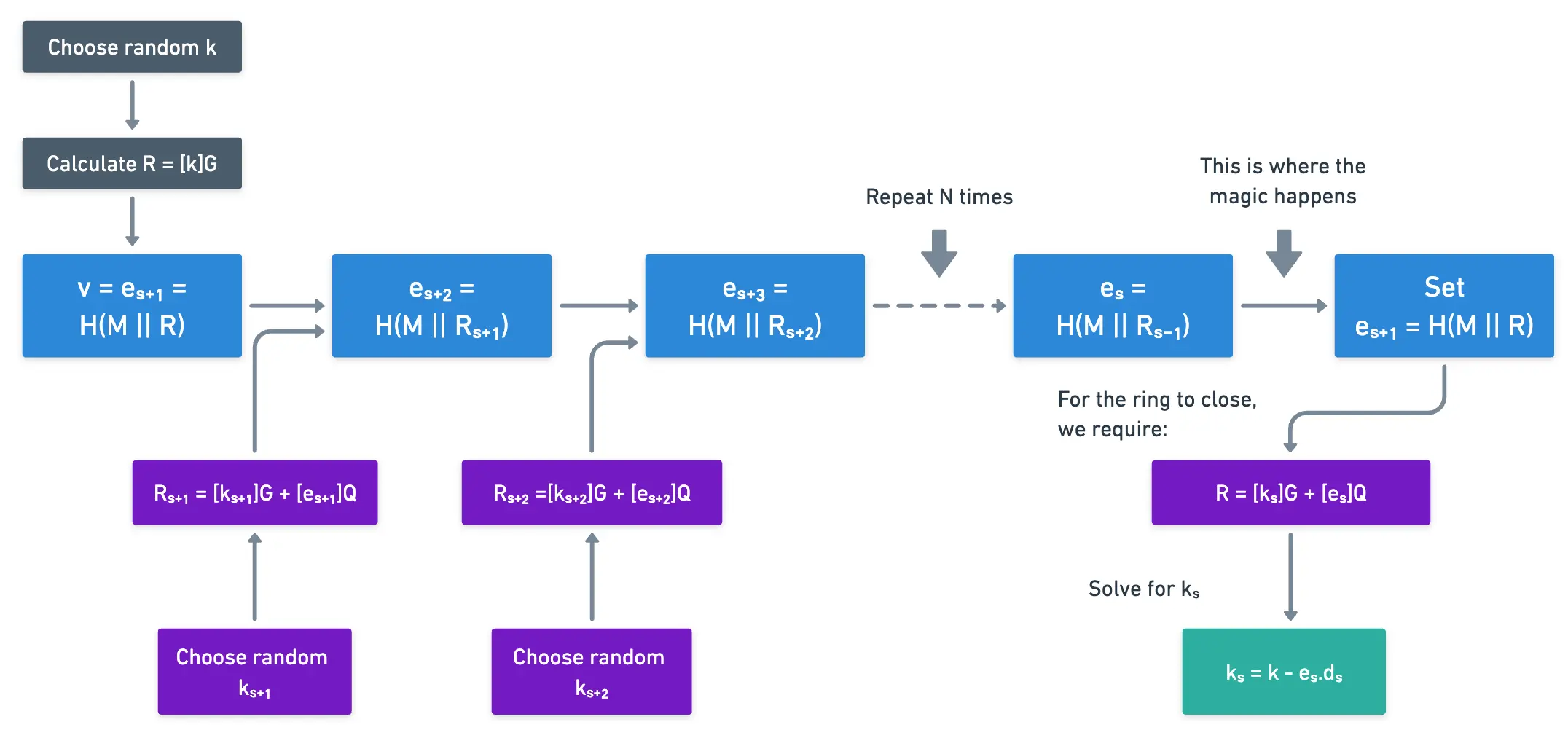
Eventualmente, Sara hace esto para todos los participantes, obteniendo así un desafío final, que simplemente llamaremos $e$. Lo hace en orden, comenzando por ella misma (s), y luego calculando $e_{s+1}$. Continúa con este proceso, y al llegar al participante $p$, cuenta desde $1$ hasta $s$. Esto es crucial, porque la firma se evaluará exactamente en este mismo orden.

$$e_{s+1} \rightarrow e_{s+2} \rightarrow ... \rightarrow e_p \rightarrow e_1 \rightarrow ... \rightarrow e_{s-1} \rightarrow e_s$$

Todo lo que queda es que ella cierre el anillo, lo que significa que el cálculo final debería devolver el valor inicial, entonces $e_{s+1} = v$. Para esto, tiene que encontrar algún valor $k_s$ tal que:

$$R_s = [k_s]G + [e_s]Q$$ $$e_{s+1} = H(M || R_s)$$

Como sabemos que $e_{s+1} = v = H(M || R)$, todo lo que necesitamos es encontrar un valor de $k_s$ tal que $R = R_s$. Moviendo un poco las cosas:

$$R = R_s \Rightarrow [k]G = [k_s]G + [e_s]Q$$ $$\mathcal{O} = [k_s]G + [e_s.d_s]G - [k]G = [k_s + e_s.d_s - k]G$$ $$k_s = k - e_s.d_s$$

Podemos obtener el valor deseado para $k_s$. Y la firma final es la tupla:

$$(e_1, k_1, k_2, ..., k_p)$$

Es importante que los valores se proporcionen en el orden del anillo. Sara estará en algún lugar en el medio, oculta...

Aquí hay una representación visual de todo el proceso de firma, para ayudar a comprender mejor todos los pasos involucrados:

Click to zoom

Verificación

Todo lo que queda es verificar la firma. Para esto, Bruno comienza desde $e_1$, y calcula lo siguiente para cada participante $i$:

• El valor $R_i = [k_i]G + [e_i]Q_i$
• Y el siguiente desafío, como:

$$e_{i+1} = H(M || R_i)$$

Si el bucle se cierra correctamente, lo que significa que el desafío final produce exactamente $e_1$, entonces él acepta la firma. Ten en cuenta que el anillo se cierra porque nos aseguramos de encontrar un $k_{s-1}$ adecuado para Sara. ¡Y hicimos esto usando la clave privada de Sara — si no la conociéramos, entonces encontrar el $k_{s-1}$ correcto no es una tarea fácil.

Desde el punto de vista del verificador, todos los valores $k$ son indistinguibles entre sí (son solo números), por lo que no puede saber cuál es el calculado — ¡recuerda que los otros son simplemente aleatorios!

Muy bien, eso fue ciertamente mucho.

Advertencia: sumatorias adelante. Toma un respiro. Hidrátate. Pausa por un minuto.

¿Listo? Sigamos adelante.

Multifirmas

La idea es simple: ¿qué pasa si requerimos que múltiples participantes firmen algo? Y esto no es tan descabellado: a menudo es un requisito al firmar documentos legales del mundo físico. Se siente como una extensión muy natural.

Las multifirmas son especialmente útiles al firmar operaciones sensibles. Por ejemplo, las acciones administrativas en una aplicación podrían requerir una firma de múltiples miembros de una organización. Esto asegura que ningún actor individual tenga privilegios de administrador, y que no exista un único punto de fallo.

Click to zoom

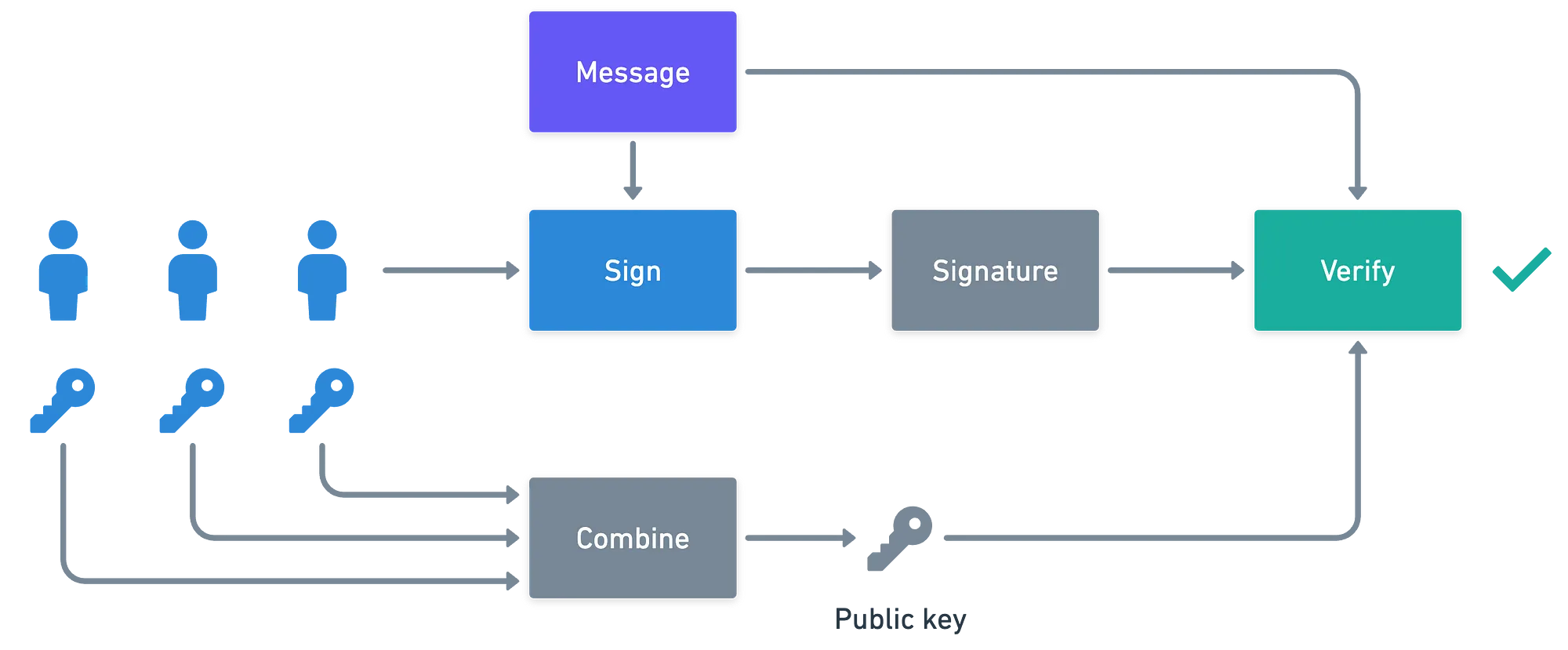
Siguiendo el patrón de ejemplos anteriores, demos un breve resumen antes de sumergirnos en las matemáticas:

Las multifirmas permiten que múltiples usuarios firmen un solo mensaje, de modo que la firma no es válida si no ha sido firmada por suficientes usuarios

Hay múltiples formas de hacer esto.

Multifirmas de Schnorr

Las firmas de Schnorr tienen una propiedad muy agradable: son lineales. En términos simples, esto significa que podemos sumar firmas individuales y aún terminar con una firma válida. No hay inversos multiplicativos complicados en la mezcla que podrían potencialmente complicar las cosas.

Debido a esto, podemos adaptar el esquema que ya presentamos, para que múltiples participantes puedan firmar un mensaje.

La configuración es ligeramente diferente de lo habitual: cada uno de los $p$ participantes tiene una clave privada $d_i$, y tiene una clave pública como $Q_i = [d_i]G$. También necesitaremos una clave pública combinada $Q$, calculada como:

$$Q = \sum_{i=1}^p Q_i$$

Ten en cuenta que este es exactamente el mismo resultado que si hubiéramos sumado las claves privadas primero, y luego calculado $Q$:

$$\left [ \sum_{i=1}^p d_i \right ]G = \sum_{i=1}^p [d_i]G = \sum_{i=1}^p Q_i$$

Después, la firma ocurre de la siguiente manera:

• Cada participante elige un número aleatorio $k_i$, y calcula $R_i = [k_i]G$.
• Luego, los $R_i$ individuales se combinan así:

$$R = \sum_{i=1}^p R_i$$

• Con esto, se calcula un desafío $e$ como $e = H(R || M)$.
• Luego, cada participante calcula una firma individual $s_i$:

$$s_i = k_i - e.d_i \ \textrm{mod} \ n$$

• Finalmente, las firmas parciales se suman para producir un solo $s$, como:

$$s = \sum_{i=1}^p s_i \ \textrm{mod} \ n$$

Y como antes, la firma producida es el par $(e, s)$. Curiosamente, ¡este par se verifica exactamente como una firma normal de Schnorr! El verificador calcula $R' = [s]G + [e]Q$, y acepta si $e = H(R' || M)$. Aquí es donde entra la linealidad: podemos mostrar que $R'$ debería ser igual a $R$, y por lo tanto la firma debería funcionar.

$$R' = [s]G + [e]Q = \left [ \sum_{i=1}^p s_i + e.\sum_{i=1}^p d_i \right ]G = \left [ \sum_{i=1}^p k_i + e.d_i - e.d_i \right ]G$$ $$R' = \left [ \sum_{i=1}^p k_i \right ]G = \sum_{i=1}^p [k_i]G = \sum_{i=1}^p R_i = R$$

Recuerda que estoy omitiendo intencionalmente las operaciones módulo $n$ para mantener las cosas lo más simples y limpias posible. ¡El tratamiento riguroso requiere que tengas en cuenta la operación!

Y así, ¡múltiples participantes han producido una sola firma! ¡Genial!

Firmas de Umbral (Threshold)

Las firmas de umbral ofrecen una funcionalidad ligeramente más avanzada. El término umbral alude al hecho de que se requerirá un cierto número mínimo de firmantes para que la firma sea válida. Requerimos que $t$ participantes de un grupo de $m$ personas participen en la firma, para producir una firma.

Como siempre, vamos a necesitar una clave privada. Pero como antes, el punto es que ningún actor individual la conoce — solo tienen acciones o partes de ella. Lograr esto en el caso de firmas de umbral no es trivial — uno no simplemente elige un entero aleatorio, como era el caso de otros esquemas.

De hecho, la generación de claves es un paso crucial para que las firmas de umbral funcionen.

En verdad, entender las firmas de umbral implica usar polinomios, que aún no hemos cubierto. Serán el tema central en próximas entregas. Por ahora, debemos contentarnos con conocer la existencia de este tipo de firmas. Volveremos a ellas más adelante en la serie.

Resumen

Las firmas vienen en muchos sabores diferentes. Al final, todo se trata de crear un juego criptográfico que tenga propiedades específicas. Cualquier necesidad que puedas tener, probablemente puedas idear una estrategia que la cubra.

¿Necesitas firma anónima pero con un administrador que pueda revocar firmas? Las firmas de grupo están ahí para salvarte. ¿Quieres alterar el mensaje, pero mantener una firma válida? Las firmas homomórficas son lo tuyo.

Ahora hemos visto un número significativo de aplicaciones criptográficas basadas en grupos. Es hora de profundizar nuestra comprensión de los grupos un paso más — así que la próxima vez, veremos homomorfismos e isomorfismos de grupos. Y a su vez, cubriremos una nueva técnica criptográfica útil.