Criptografía 101: Polinomios

Este artículo forma parte de una serie más larga sobre criptografía. Si este es el primer artículo con el que te encuentras, te recomiendo comenzar desde el principio de la serie.

Hasta ahora en la serie, hemos invertido mucho en profundizar nuestra comprensión de la Criptografía de Curvas Elípticas (ECC). Tomamos un breve desvío para introducir las funciones de hash, pero eso es lo máximo que nos hemos desviado de nuestro tema central.

Aunque la ECC es muy rica y poderosa, hay mucho más en criptografía que solo eso. Y en esta sección, quiero presentarte el fantástico mundo de los polinomios.

Podemos hacer algunas cosas con ellos que no se pueden lograr con curvas elípticas. Así que comencemos presentándolos, y luego veremos sus aplicaciones. ¡Vamos!

Polinomios

Probablemente hayas visto a estos muchachos en algún momento durante la secundaria. En esencia, son muy simples: consisten en una expresión que involucra variables, que solo pueden ser sumadas, restadas y multiplicadas. La multiplicación también implica que podemos tener potencias de variables. Y cada término en la suma puede ser multiplicado por un número, llamado coeficiente. Algo como esto:

$$P(x,y) = x^4 + 3yx^3 - y^2x^2 + 6y - 1$$

Podemos notar que un polinomio puede tener múltiples variables diferentes. No hay limitación en este sentido, pero en la mayoría de los casos, solo usaremos una variable y la denotaremos como $x$.

Como curiosidad, sumar dos polinomios da como resultado otro polinomio, y multiplicar dos polinomios también da como resultado otro polinomio; debido a esto, el conjunto de todos los polinomios forma un objeto matemático llamado anillo.

Los polinomios tienen aplicaciones en varias áreas de las matemáticas. También son útiles en criptografía, pero bajo una condición: debemos usar enteros en todas partes. Esto significa que a las variables solo se les darán valores enteros, y no podemos tener polinomios con coeficientes como $0.5$. Esto garantiza que el polinomio exclusivamente genere enteros como resultado.

Además, en criptografía, normalmente operamos bajo la operación módulo. Así que una expresión completa para el polinomio, si quieres, se vería algo así:

$$P(x) = x^4 + 3x^3 - x^2 + 6 \ \textrm{mod} \ q$$

Finalmente, el grado de un polinomio se define por la potencia más alta a la que se eleva la variable. Por ejemplo, el polinomio que acabamos de ver tiene grado $4$.

Este es típicamente el punto donde uno comenzaría a preguntarse "¿por qué necesito saber sobre esto?"

Sí, lo sé. Prometo que las aplicaciones serán muy interesantes. Por favor, ten paciencia, porque todavía necesitamos introducir un tipo particular de polinomio que resultará extremadamente útil para nosotros: los Polinomios de Lagrange.

Interpolación

¿Alguna vez has notado cómo solo hay una única línea posible que pasa por dos puntos?

Click to zoom

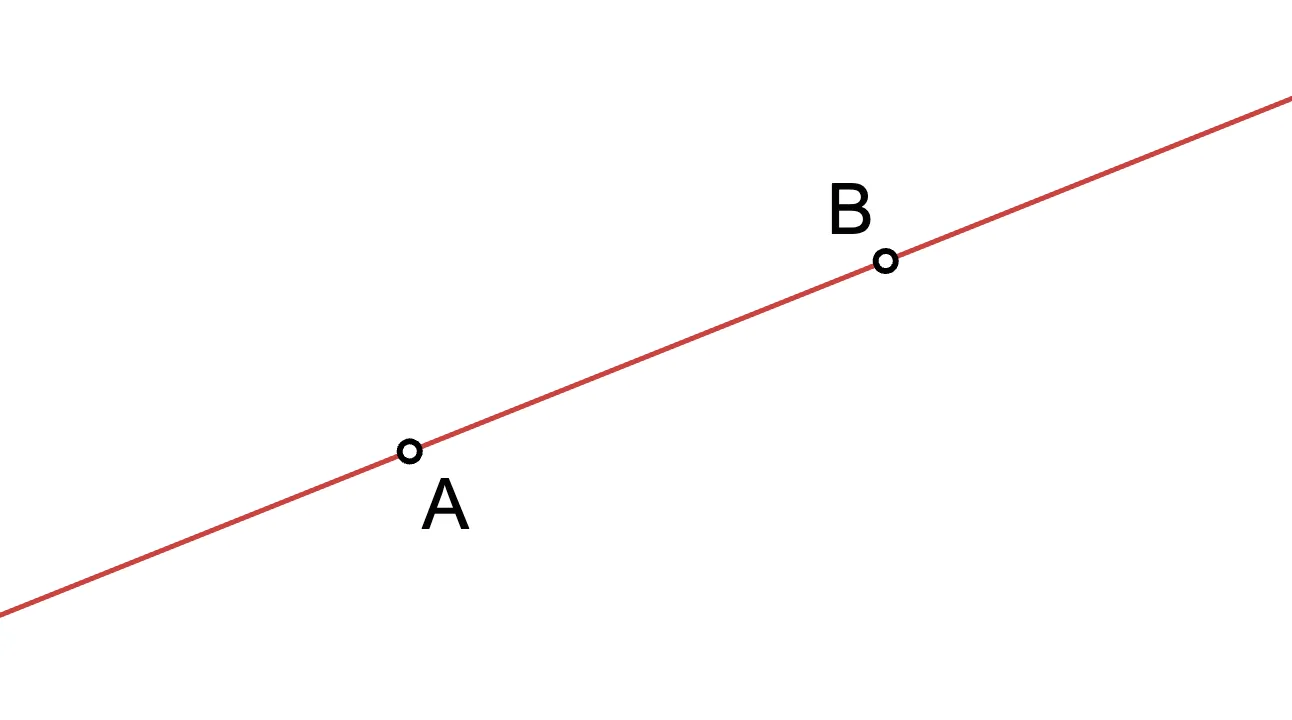
Por mucho que lo intentes, no hay otra línea que pase por $A$ y $B$. Y una línea es realmente una función polinómica, $P(x) = m.x + n$. Y esto no es una coincidencia.

Intentemos ahora con tres puntos. Pueden estar alineados, en cuyo caso puedes dibujar una línea que pase por ellos, o no alineados. En el último caso, puedes dibujar una, y solo una parábola (un polinomio de grado 2) que pase por ellos.

Click to zoom

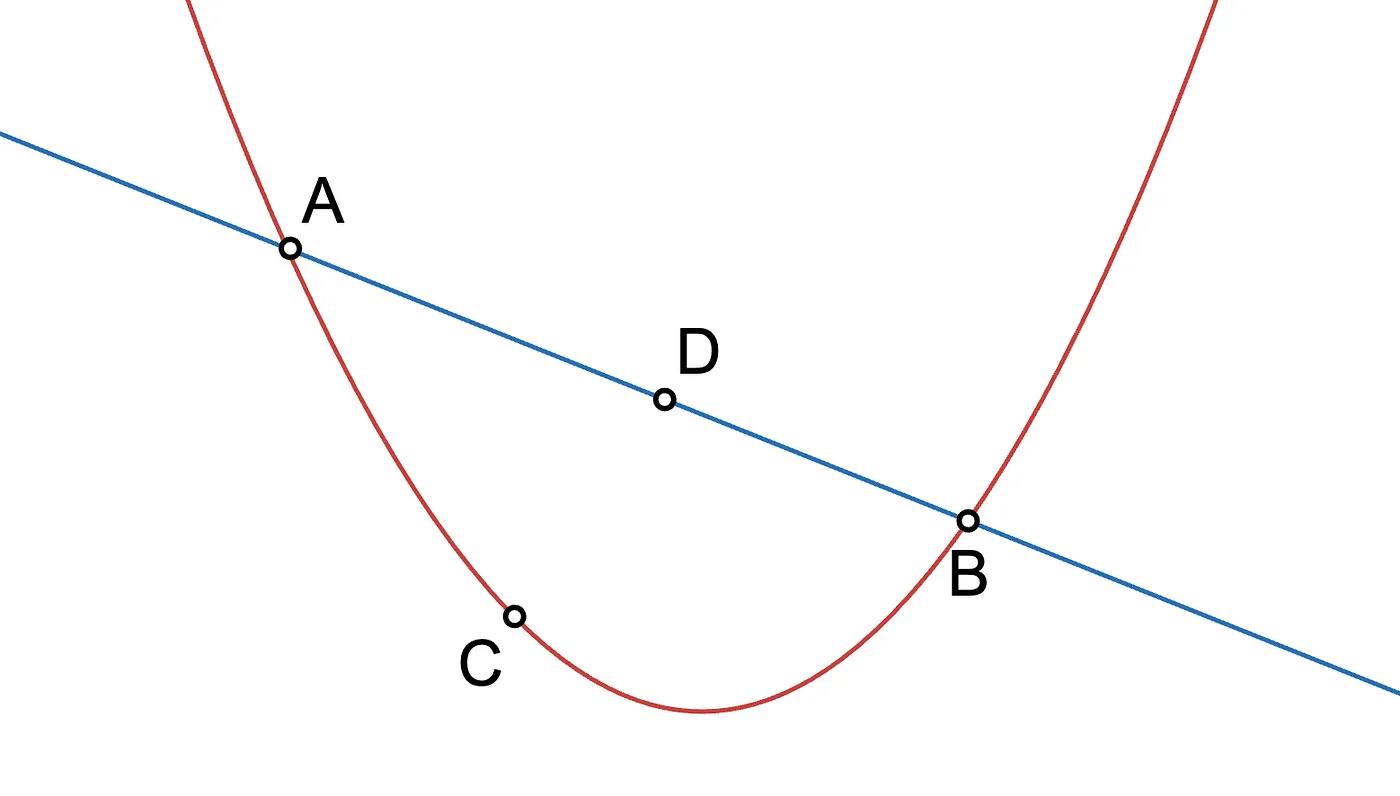
Solo para aclarar, ya que usamos enteros y la operación módulo, las curvas son solo una forma de visualizar lo que está sucediendo, pero realmente usamos puntos discretos.

En general, para un conjunto dado de $m$ puntos, hay un polinomio único de grado como máximo $m - 1$, que pasa por todos los $m$ puntos. Este polinomio es muy especial, tanto que recibe su propio nombre: un Polinomio de Lagrange. Decimos que interpola los $m$ puntos.

¿Qué lo hace tan especial? Para entenderlo, hagamos un pequeño ejercicio:

Toma tres puntos cualquiera con valores enteros $(x_1, y_1)$, $(x_2, y_2)$ y $(x_3, y_3)$. Sabemos que una parábola interpola estos tres puntos, por lo que nuestro polinomio de Lagrange se verá así:

$$L(x) = ax^2 + bx + c$$

Todavía no sabemos cómo calcular el polinomio interpolador, pero eso está bien por el momento. Ahora, toma un montón de valores de $x$ y calcula $L(x)$ para cada uno de ellos; obtenemos muchos puntos que pertenecen a la misma parábola.

Click to zoom

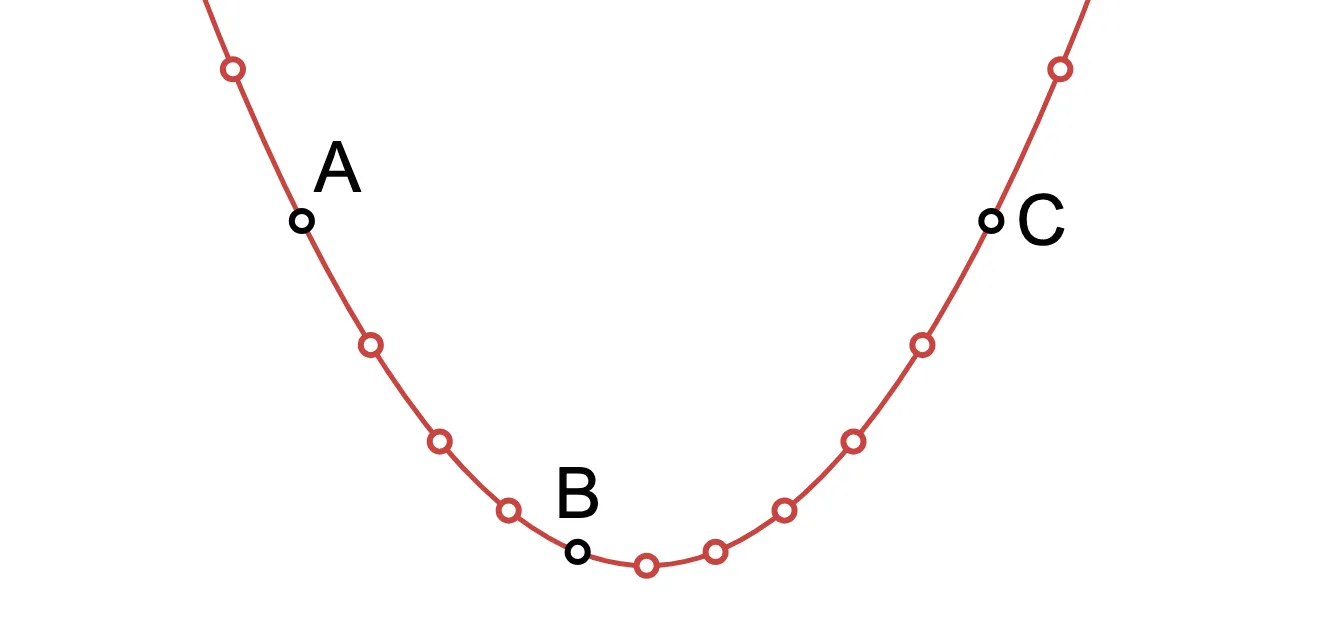
Y aquí está lo interesante: cualquier conjunto de tres o más puntos del dibujo anterior produce el mismo polinomio interpolado.

Y de nuevo, probablemente todavía te estés preguntando "bien, pero ¿por qué necesito saber estas cosas?"

Está bien, está bien. Tienes razón. Suficiente teoría. ¡Veamos cómo es una aplicación, antes de que pierda tu interés! Aquí está.

Codificación de Borrado

Cada vez que envías un video a través de una aplicación de mensajería, esperas que el receptor lo reciba en una sola pieza inalterada, ¿verdad? Pero si profundizamos un poco, no es realmente así como se transmite la información. No envías un solo paquete de información por internet, como si fuera un paquete comprado en Amazon.

Lo que realmente sucede es que el video original se envía en pequeñas piezas, llamadas paquetes de información. Y en tu dispositivo, en el dispositivo del destinatario y en muchos lugares intermedios, hay procesos ejecutándose (hola, TCP) que aseguran que cada paquete llegue a su destino, mientras se encargan del laborioso proceso de reconstruir el video original a partir de sus piezas.

Y durante sus viajes, muchas veces, los paquetes de información se pierden o se corrompen. Sí, lo has oído bien. Y los procesos que mencionamos remedian esta complicación volviendo a solicitar cualquier paquete perdido.

Pero hay otra forma de abordar este problema: introducir redundancia en nuestros datos.

Click to zoom

Redundancia significa que efectivamente vamos a enviar más información de la que realmente se necesita. Piensa en nuestro video como algo divisible en cuatro pequeños fragmentos de información; entonces enviaríamos un número de fragmentos mayor que cuatro. E incluso si se pierde información en el camino, el destinatario aún puede reconstruir los datos originales.

¿Pero Cómo?

Polinomios, así es cómo.

Como siempre, todo comienza con una idea simple: las piezas originales de datos pueden ser los coeficientes de un polinomio.

$$P(x) = a_0 + a_1x + a_2x^2 + ... + a_{m-1}x^{m-1} = \sum_{i=0}^{m-1} a_ix^i$$

Cada pieza de datos es solo un número binario, es decir, solo un entero. Y recuerda, podemos reconstruir un polinomio de grado $m - 1$ a partir de al menos $m$ puntos (mediante interpolación de Lagrange). ¿Puedes ver cómo continúa esto?

Solo tenemos que evaluar $P(x)$ en $k$ puntos diferentes $x$, y requerimos que $k$ sea mayor que $m$. ¿Cuántos más, te preguntarás? Eso depende de cuántos paquetes esperas perder, porque los puntos $(x, P(x))$ serán de hecho los paquetes a enviar a través de la red.

Y por supuesto, el receptor puede reconstruir el polinomio original mediante interpolación, usando cualquiera de los $m$ puntos de los $k$ totales. ¡Y al recuperar los coeficientes, efectivamente reconstruyen el mensaje original!

Esta técnica se conoce como códigos correctores de errores Reed-Solomon. Una aplicación interesante para ellos está en las comunicaciones del espacio profundo, donde ocurren errores y corrupción de datos al transmitir información a través de vastas distancias. Interesante, ¿verdad?

Interpolación, Revisitada

Ahora conocemos al menos una aplicación para los polinomios de Lagrange. Pero todavía no sabemos cómo interpolar.

La forma estándar o directa de encontrar una interpolación polinómica es realmente bastante engorrosa. Encontrarás expresiones como esta:

$$\ell_j(x) = \prod_{\substack{0 \leq m \leq k \\ m \neq j}} (x - x_m)(x_j - x_m)^{-1}$$ $$L(x) = \sum_{j=1}^m y_j\ell_j(x)$$

Quiero decir, podemos manejar estas ecuaciones, sin problema, pero el asunto es que esta no es realmente la forma más eficiente de interpolar un conjunto de puntos.

Para aquellos que conocen la notación Big O, la interpolación directa resulta ser $\mathcal{O}(n^2)$. Y el algoritmo más eficiente conocido hoy en día, el que se presenta a continuación, es $\mathcal{O}(n.log(n))$.

La mejor y más rápida manera de interpolar es usar el algoritmo de Transformada Rápida de Fourier (FFT por sus siglas en inglés). No entraremos en detalles sobre cómo funciona esto, porque involucra algunos conceptos que no hemos introducido, como las raíces de la unidad en un grupo.

Sin embargo, existen excelentes recursos si estás interesado en diseccionar las entrañas del algoritmo. Si eso es lo tuyo, ¡diviértete!

Compartición de Secretos

Finalmente, veamos otra aplicación, que resultará muy útil para diseñar protocolos más familiares como las firmas. Echemos un vistazo a la Compartición de Secretos de Shamir.

¿Recuerdas cómo el Intercambio de Claves de Diffie-Hellman permitía a múltiples partes generar un secreto compartido? Bueno, tiene una limitación: el secreto es generado.

Lo que esto significa es que si yo, Franco, quiero revelar un valor secreto específico a un grupo de personas, entonces Diffie-Hellman no es adecuado para la tarea. Debemos pensar en otra estrategia.

Y de nuevo, los polinomios salvan el día. Así es cómo:

• Establece el valor secreto $s$ como el término independiente (el coeficiente que no está multiplicado por $x$).
• Luego, selecciona $m$ números aleatorios como coeficientes para un polinomio, $P(x)$.
• Para terminar, elige $k$ valores de $x$ y evalúa $y = P(x)$ en todos estos valores.

Terminas con un montón de puntos $(x, y)$. Y como sabes, cualquier conjunto de $m + 1$ de estos puntos puede usarse para reconstruir el polinomio original, $P(x)$.

Entonces, ¿y ahora qué? Supongamos que me comunico con participantes en una red. Comparto $(x_1, y_1)$ con Alicia, luego $(x_2, y_2)$ con Bruno, $(x_3, y_3)$ con Carlos, y así sucesivamente. Luego comienzan a comunicarse entre ellos: Alicia envía $(x_1, y_1)$ a Bruno, Carlos envía $(x_3, y_3)$ a Alicia, etc.

Lo que sucede es que, en algún momento, Alicia tendrá suficientes piezas para reconstruir el polinomio $P(x)$. Y esto es genial, porque entonces mira el coeficiente independiente, ¡y ese es exactamente el secreto que quería compartir!

Este es un ejemplo de un amplio conjunto de técnicas conocidas como Computación Multi-Parte (MPC). Es un tema muy interesante que ampliaremos en artículos futuros.

Resumen

Curvas elípticas, hashing, polinomios: ¡nuestro conjunto de herramientas sigue creciendo! Y a medida que acumulamos más herramientas, nuevas técnicas criptográficas se vuelven disponibles para nosotros. En particular, podemos combinar firmas y polinomios para producir una nueva construcción interesante: firmas de umbral. Entraremos en detalle en el próximo artículo, estirando los límites de lo posible con las herramientas actualmente a nuestra disposición.