Criptografía 101: Firmas de Umbral

Este artículo forma parte de una serie más larga sobre criptografía. Si este es el primer artículo con el que te encuentras, te recomiendo comenzar desde el principio de la serie.

En el artículo anterior, aprendimos sobre polinomios y vimos un par de sus aplicaciones.

Sin embargo, esta nueva pieza de criptografía parece estar desconectada de todo lo que hemos aprendido hasta ahora. No obstante, hay formas interesantes de combinarla con conceptos previos, como las firmas digitales.

Este artículo estará dedicado exclusivamente a explicar un ejemplo de esto, donde combinaremos las técnicas de firma habituales con polinomios, para crear un interesante esquema híbrido. Trabajaremos en el contexto de curvas elípticas, y usaremos $G$ y $H$ para denotar generadores de grupo para un grupo $\mathbb{G}$.

Basaré ligeramente mi explicación en este artículo, con algunos ajustes con la esperanza de hacer las cosas más fáciles de entender.

Aun así, una advertencia amistosa: las firmas de umbral (threshold) no son simples de explicar. Hay muchos matices que tendremos que aclarar. Así que primero veamos un breve resumen de qué son y qué hacen, antes de sumergirnos realmente en las matemáticas detrás de ellas.

Justo los Firmantes Necesarios

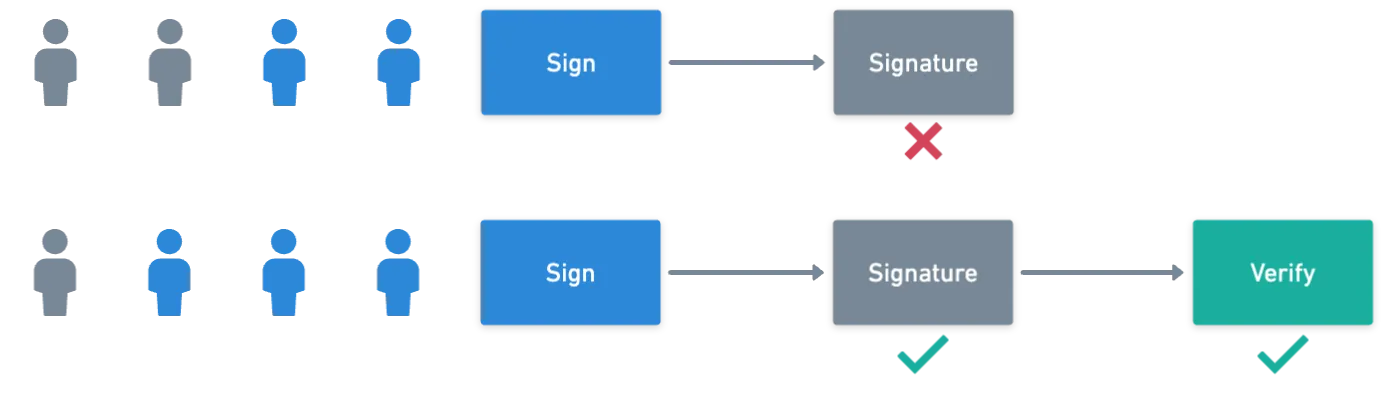
Las firmas de umbral son un tipo de multifirma, lo que significa que se requieren múltiples participantes para firmar un mensaje. Pero esta vez, no es necesario que todos los participantes lo hagan.

Imagina un grupo de diez personas que tienen privilegios de administrador para una aplicación. Para realizar alguna acción sensible, requerimos al menos tres aprobaciones.

De esta manera, no tenemos que molestar a todos los administradores al mismo tiempo; basta con un subconjunto de firmantes disponibles.

Esto se siente como una mejora al esquema de multifirma que exploramos anteriormente, donde se requería que todos los firmantes participaran. Pero en realidad, lograr este resultado implica flexionar algunos músculos criptográficos adicionales.

Click to zoom

Podemos dividir las firmas de umbral en tres pasos principales o algoritmos (como la mayoría de los esquemas de firma):

• Generación de claves (KeyGen), que es un algoritmo que genera un par de claves privada compartida y pública,
• Firma, donde un mensaje se procesa junto con la clave privada y un nonce para obtener un par $(r, s)$,
• Y verificación, el paso donde la firma se valida contra el mensaje y la clave pública.

Cuando trabajamos con esquemas de firma de umbral, los pasos de generación de claves y firma, que eran bastante directos en ejemplos anteriores, serán reemplazados por procesos más complejos que involucran comunicaciones entre los firmantes. Afortunadamente, la verificación sigue siendo la misma, por lo que nuestro enfoque estará en los dos primeros pasos.

Nota que la idea de requerir un umbral de firmantes es muy reminiscente de la cantidad mínima de puntos para reconstruir un polinomio mediante interpolación. Y de hecho, esto está en el núcleo de cómo funcionan las firmas de umbral.

Además, para mantener las cosas claras, debemos decir que los firmantes o participantes están ordenados. Cada uno tendrá un identificador o índice, que va desde $1$ hasta $n$, el número total de participantes.

Nuestros objetivos están establecidos, y la introducción ha terminado. ¿Vamos a lo bueno?

Preliminares

En los protocolos de umbral, compartir información es clave. En última instancia, la capacidad de un conjunto de firmantes para compartir información es lo que les permitirá producir firmas.

Ya hemos visto que compartir un secreto se puede lograr con la Compartición de Secretos de Shamir (SSS). La idea era evaluar un polinomio en muchos valores diferentes y compartir los resultados como puntos. Y con esos puntos, podríamos interpolar el polinomio original.

Pero hay un problema. ¿Cómo puede un receptor verificar si los valores que recibe están calculados correctamente? O, en otras palabras, ¿hay alguna forma de probar que los puntos están efectivamente relacionados con el polinomio original?

Y te puedes estar preguntando por qué los valores podrían ser incorrectos. ¿Por qué alguien enviaría un valor erróneo? Hay al menos dos razones a considerar: errores en la comunicación y actividad maliciosa. Es posible que un atacante esté tratando de romper nuestro modelo de firma; no podemos esperar necesariamente que todos se comporten correctamente, y debemos tomar medidas para mitigar este posible escenario.

Para abordar esta preocupación, necesitaremos una nueva herramienta.

Compartición de Secretos Aleatoria Verificable

Lo que hacemos es pedirle al compartidor que haga un compromiso. Esto vinculará al compartidor con su información secreta (su polinomio), para que más tarde simplemente no pueda producir valores inválidos.

Esta idea es la que está detrás de la Compartición de Secretos Aleatoria Verificable (VRSS por sus siglas en inglés), una especie de reemplazo directo para SSS. Lo que queremos hacer es comprometernos con los coeficientes de nuestro polinomio, y para esto, necesitaremos no uno, sino dos de ellos:

$$f_i(x) = a_{i,0} + a_{i,1}x + a_{i,2}x^2 + ... + a_{i,t}x^t$$ $$f_i'(x) = b_{i,0} + b_{i,1}x + b_{i,2}x^2 + ... + b_{i,t}x^t$$

¿Por qué, preguntas? Porque los compromisos necesitan ser ocultadores. No queremos revelar los coeficientes, así que sus compromisos deben estar cegados. ¡Los coeficientes del segundo polinomio son de hecho estos factores de cegado!

Así que usando nuestros generadores de grupo, cada participante $i$ calcula y transmite los valores de compromiso $C_i$, uno para cada uno de los coeficientes en los polinomios:

$$C_{i,m} = [a_{i,m}]G + [b_{i,m}]H$$

¡Genial! Ahora todo lo que queda es compartir. Y para esto, todos necesitarán evaluar su polinomio. Como cada participante tiene un índice $j$, podemos elegir evaluar la parte para un jugador objetivo en su índice, así $f_i(j)$.

Esto significa que los individuos obtendrán $f_i(j)$ y $f_i'(j)$ de algún otro participante $i$.

Y al recibir estos valores, el participante $j$ puede validarlos de la siguiente manera:

$$[f_i(j)]G + [f_i'(j)]H = \sum_{m=1}^{t-1} [(j)^m]C_{i,m}$$

¡Eso es básicamente todo! Ahora tenemos un mecanismo para compartir información secreta, de una manera que es verificable. Con esta herramienta, podemos comenzar a construir nuestro esquema de firma.

Generación de Claves

Dado que hay múltiples partes involucradas en las firmas de umbral, cada participante tendrá un entero $d_i$ como su parte (o pieza) de una clave privada.

Sin embargo, esto no es un entero elegido al azar, como de costumbre. En cambio, los participantes se involucran en un proceso donde interactúan entre sí, produciendo finalmente su parte de la clave privada. Este tipo de protocolos se llaman algoritmos de Generación de Claves Distribuida (DKG).

Y podemos usar VRSS para construir nuestro algoritmo. ¡Qué conveniente!

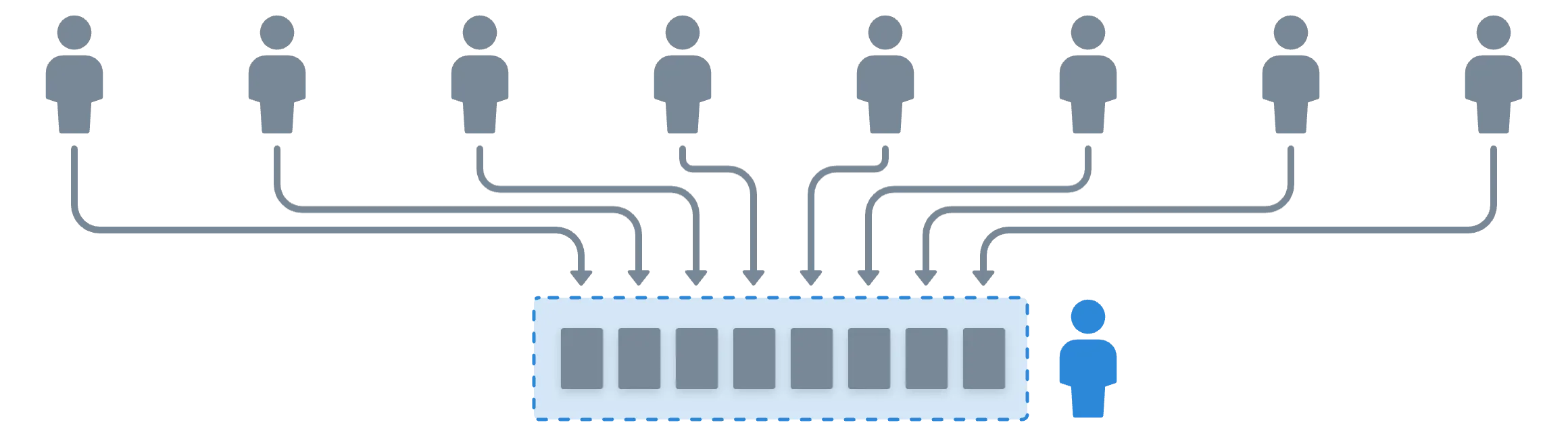
La idea es que cada participante recibirá una parte de cada uno de sus pares, y usarán estos valores verificados para calcular su parte de la clave privada:

$$d_i = \sum_{j=1}^m f_j(i)$$

Es posible que algunos valores no pasen la verificación; algunas partes pueden ser descalificadas en este caso. Es por eso que VRSS es importante.

Aún así, seguiremos el camino feliz para mantener las cosas relativamente simples.

El resultado del DKG es una pieza de una clave privada compartida, $d$. Ninguna de las partes involucradas en este protocolo conoce este valor, solo sus piezas.

Click to zoom

Finalmente, necesitamos una clave pública. Y para esto, cada participante transmite su coeficiente secreto independiente o cero, $a_{i,0}$. Este secreto no puede ser revelado como tal, y por lo tanto, se transmite como una parte de clave pública:

$$Q_i = [a_{i,0}]G$$

Creo que es bastante extraño ver que la parte de la clave pública se calcule así. ¡Apuesto a que esperabas ver $d_i$ ahí dentro!

Hay una buena razón para que no se use de esa manera. Volveremos a esta afirmación más tarde, porque necesitaremos definir un par de cosas para entender lo que realmente está sucediendo.

Una vez que todas las partes son públicas, cada participante puede calcular la clave pública global de forma independiente:

$$Q = \sum_{i=0}^m Q_i$$

Para concluir, aquí va un breve resumen de este paso:

La generación de claves implica que las partes se comuniquen entre sí, generando piezas de una clave privada compartida. Ningún jugador conoce la clave privada compartida. También se calcula una clave pública asociada con el secreto compartido.

Con todas las claves en su lugar, todo lo que queda es firmar.

Firmando un Mensaje

Lo primero que necesitaremos es un mensaje para firmar. Pero esto no es trivial, porque todos necesitan estar de acuerdo en un mensaje. No cubriremos cómo sucede esto; simplemente asumamos que todos conocen el mensaje $M$ que se está firmando.

En ECDSA, un firmante normalmente elegiría un nonce aleatorio $k$, y calcularía un desafío $R = [k]G$ en consecuencia, produciendo una firma como esta:

$$s = k^{-1}(H(M) + d.r) \ \textrm{mod} \ n$$

Pero como ya hemos visto, así no es como tiende a operar la criptografía de umbral. En cambio, un grupo de $t$ firmantes se comunicará entre sí para producir una firma. Y lo primero que necesitarán es un nonce.

Afortunadamente, ya tenemos una herramienta para generar un valor distribuido: ¡DKG! Digamos que los firmantes ejecutan una ronda de DKG, obteniendo una parte $k_i$, y un desafío asociado:

$$R_i = \sum_{i=0}^m R_i$$

Para el cálculo de la firma, todos utilizarán la coordenada x de $R$, que denotaremos como $r$.

Construyendo la Firma

Como probablemente puedas adivinar a estas alturas, la generación de la firma también se realiza en partes. Y nuevamente, la idea es que solo cuando está disponible un cierto número de partes, podremos producir una firma válida a través de la agregación de estas partes calculadas independientemente.

Nuestro requisito es el siguiente: las partes de firma $s_i$ deberían interpolar a la firma final $s$, que debería pasar la verificación cuando se usa la clave pública $Q$. Lo más natural que podemos hacer aquí es adaptar la expresión de $s$ para que use partes de sus componentes en su lugar:

$$s_i = k_i^{-1}H(M) + k_i^{-1}d_i.r \ \textrm{mod} \ n$$

¿Pero esto tiene sentido? Aquí, tenemos una suma, multiplicaciones e incluso inversos modulares. No parece obvio asumir que esto funcionará así sin más.

Parece justo que examinemos esta expresión y verifiquemos que funciona correctamente. Y realmente, no es tan complicado como podrías imaginar. Tomémoslo con calma, paso a paso.

Interpolando Sumas

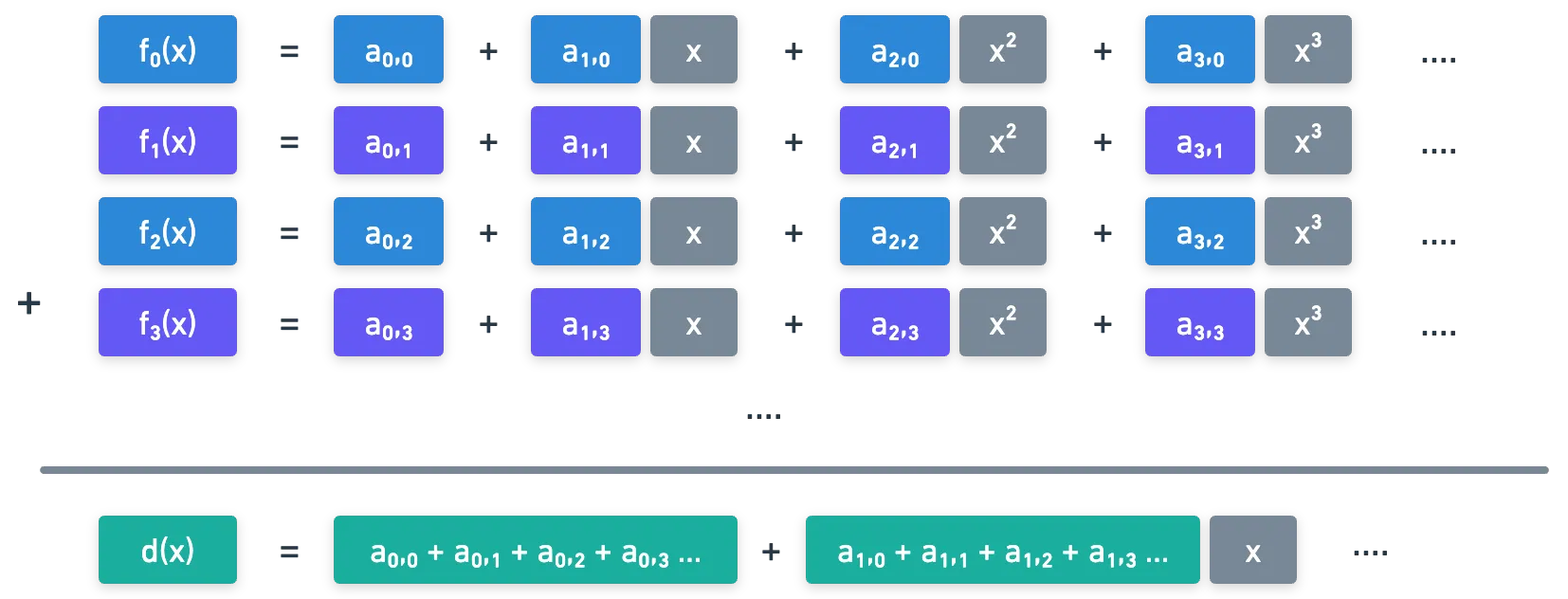
Para empezar, digamos que tenemos dos polinomios $a(x)$ y $b(x)$. Si los evaluamos en diferentes valores $i$, obtenemos conjuntos de puntos de la forma $(i, a(i))$ y $(i, b(i))$. Por conveniencia, denotémoslos como $a_i$ y $b_i$:

$$a_i = (i, a(i)) b_i = (i, b(i))$$

Sabemos que cualquier subconjunto de t puntos de estos puntos nos permite interpolar los polinomios originales. Y si definimos el término independiente de $a(x)$ como $a$, podríamos escribir que:

$$a \leftarrow \textrm{interpolate}(a_1, ..., a_t)$$

Como recordatorio, en el contexto de compartir secretos, generalmente estamos interesados en el término independiente. Es por eso que cuando decimos que interpolamos algunos valores, podemos referirnos a la salida como solo este coeficiente independiente o cero, y no a todo el polinomio. ¡Pero realmente, la salida completa es todo el polinomio!

De manera similar, asumamos que tenemos puntos donde $b(x)$ tiene un término independiente $b$, y por lo tanto:

$$b \leftarrow \textrm{interpolate}(b_1, ..., b_t)$$

Ahora, ¿qué sucede si sumamos los polinomios $a(x)$ y $b(x)$?

Click to zoom

Podemos sumar término por término, y terminamos con un polinomio con el mismo grado que los originales ($t-1$), pero donde el término independiente es $g = a + b$. Además, dado que $g(x) = a(x) + b(x)$, entonces todos los puntos que interpolan a $g$, que son $(i, g(i))$, se pueden calcular como $a_i + b_i$. Y así:

$$g \leftarrow \textrm{interpolate}(a_1 + b_1, ..., a_t + b_t)$$

¡Y eso es genial! Esto significa que esencialmente podemos sumar partes de un polinomio, y al interpolar, obtendremos como resultado la suma de los secretos compartidos. ¡Estupendo!

Ahora podemos analizar el cálculo de la clave pública. Recuerda que la parte $d_i$ se calcula como la suma de los valores $f_j(i)$.

Debido a esto, $d_i$ es esencialmente una parte de una suma de polinomios, cuyo término independiente será la suma de todos los términos $a_{i,0}$. Lo que significa que ¡el resultado de interpolar todos los $d_i$ producirá esa suma!

Click to zoom

Y esa es la razón por la cual la clave pública se calcula de la manera en que lo hace. ¡Todo cuadra!

$$\sum_{i=0}^m a_{i,0} \leftarrow \textrm{interpolate}(d_1, ..., d_m)$$ $$Q = \left [ \sum_{i=0}^m a_{i,0} \right ]G = \sum_{i=0}^m [a_{i,0}]G$$

Interpolando Productos

Los productos son ligeramente más complicados. Cuando multiplicamos $a(x)$ y $b(x)$, el polinomio resultante $h(x)$ tendrá el doble del grado. Y debido a esto, necesitamos el doble de puntos para la interpolación:

$$h \leftarrow \textrm{interpolate}(a_1.b_1, ..., a_{2t-1}.b_{2t-1})$$

Y esto no es realmente óptimo, porque ahora necesitamos más valores para interpolar, lo que significa más comunicaciones entre pares.

Independientemente de este inconveniente, la buena noticia es que esto se comporta como esperamos: cuando multiplicamos $h(x) = a(x)b(x)$, los términos independientes también se multiplican, ¡y nuestros valores $a_ib_i$ también interpolarán a $h = ab$!

También vale la pena mencionar: cuando multiplicamos partes por una constante, la interpolación resultante también se multiplicará por ella:

Click to zoom

Así que si tomamos nuestras partes como $(i, k.a_i)$, entonces la interpolación producirá $k.a$. Bastante sencillo, ¿verdad?

Muy bien, solo nos queda un caso más por analizar. El dolor y el sufrimiento terminarán pronto, lo prometo.

Interpolando Inversos

Realmente, todo lo que nos falta es manejar ese maldito inverso modular. Lo que queremos es producir valores ${k_{i}}^{-1}$ que, cuando se interpolen, produzcan $k^{-1}$. Esto llevará un par de pasos. Sí.

• En primer lugar, todos ejecutarán una ronda de VRSS para producir partes $\alpha_i$. Por supuesto, estas partes interpolan así:

$$\alpha \leftarrow \textrm{interpolate}(\alpha_1, ..., \alpha_m)$$

• A continuación, cada participante calculará y transmitirá:

$$\mu_i = \alpha_i.k_i$$

• Dado que $\mu_i$ es el resultado de una multiplicación, al recibir $2t - 1$ partes, cualquiera podría interpolar este valor:

$$\mu \leftarrow \textrm{interpolate}(\mu_1, ..., \mu_{2t-1})$$

• Finalmente, cada participante calcula ${k_{i}}^{-1}$ de esta manera:

$${k_{i}}^{-1} = \mu^{-1}.\alpha_i$$

¿Cómo funciona esta magia, te preguntas? Bueno, considera esto: $μ^{-1}$ actúa como un término constante al interpolar los valores ${k_{i}}^{-1}$. Y debido a esto, terminamos con:

$$\mu^{-1}.\alpha \leftarrow \textrm{interpolate}({k_1}^{-1}, ..., {k_{2t-1}}^{-1})$$ $$\mu^{-1}.\alpha = k^{-1}.\alpha^{-1}.\alpha = k^{-1}$$

¡Y como por arte de magia, hemos construido valores que interpolan al inverso de $k$!

¡Eso es todo lo que vamos a necesitar! Revisemos nuestra calculación de firma con nuestras conclusiones recién encontradas.

Volviendo a la Firma

Si pudiéramos reconstruir cada secreto compartido, entonces el cálculo de la firma ocurriría como en el ECDSA estándar:

$$s = k^{-1}H(M) + k^{-1}dr \ \textrm{mod} \ n$$

Pero en la práctica, no queremos que eso suceda, y solo tenemos partes. Así que nos preguntamos si esto:

$$s_i = {k_i}^{-1}H(M) + {k_i}^{-1}d_ir \ \textrm{mod} \ n$$

también se interpola a $s$. Y la respuesta es un rotundo sí, porque solo estamos tratando con sumas, productos e inversos, y ya sabemos cómo se comportan estos.

Quizás el único problema aquí es que como estamos tratando con un producto de partes (el término ${k_i}^{-1}d_ir$), necesitaremos como $3t-2$ partes para interpolar. Pero dejando eso de lado, ¡estamos seguros de que interpolar los valores $s_i$ producirá el valor esperado de $s$!

Diferentes protocolos pueden hacer uso de varias técnicas para tratar de mitigar la necesidad de puntos adicionales para la interpolación, e idealmente, querríamos mantener ese número lo más cercano posible a $t$. Además, cuantos menos pasos de comunicación se necesiten, mejor.

Para finalizar, cuando cada participante calcula su parte $s_i$, simplemente la transmite. Y cuando hay suficientes partes disponibles, cualquiera puede interpolar, producir y generar $s$.

¡Y ahí lo tienes! Simple, ¿verdad?

Estoy bromeando, por supuesto: esto es cualquier cosa menos simple. Pero la idea general es lo que realmente es la conclusión clave:

Durante la firma, las partes se comunican nuevamente entre sí, generando piezas de una firma compartida. Cuando hay suficientes piezas disponibles, se puede construir la firma final; con menos piezas de las necesarias, simplemente no es posible.

La verificación ocurre como de costumbre, porque la salida de la firma es simplemente el par $(r, s)$.

Resumen

Creo que este es el artículo más técnicamente cargado que he escrito hasta ahora. Traté de mantenerlo lo más simple posible, pero hay algunas cosas que simplemente no podemos evitar explicar. Al menos, espero que esto arroje algo de luz sobre algunos aspectos que, según mi experiencia, no suelen explicarse en detalle.

🔥 Importante: En realidad hay una vulnerabilidad bastante grande en el proceso que describí, donde las partes de la clave privada se filtran al compartir $s_i$.

Esto se aborda en el artículo que usé como guía, y la solución es bastante simple. Así que, por favor, no uses este artículo para construir tus firmas de umbral, ¡y tal vez consulta el artículo real en su lugar!

Diseñar este tipo de protocolos de Computación Multi-Parte, donde hay comunicación entre las partes, requiere considerar que puede existir actividad maliciosa. Así que en general, estos protocolos están llenos de rondas de descalificación, pruebas de corrección, tal vez incluso algo de cifrado y otras cosas divertidas. Realmente, son una consolidación de muchas técnicas diferentes, y tienden a ser complejos.

La Computación Multi-Parte es, en general, bastante compleja.

Este es realmente el esquema más simple que pude encontrar en términos de qué herramientas se necesitan, y se presenta principalmente con la esperanza de ilustrar los componentes principales de estas técnicas. Y esto significa que cuantas más herramientas podamos acumular, más fácil será elaborar esquemas más complejos.

Dicho esto, nuestro viaje continuará presentando otra herramienta extremadamente poderosa, que desbloqueará nuevos tipos de funcionalidad: emparejamientos. ¡Nos vemos en el próximo artículo!