Criptografía 101: Homomorfismos e Isomorfismos

Este artículo forma parte de una serie más larga sobre criptografía. Si este es el primer artículo con el que te encuentras, te recomiendo comenzar desde el principio de la serie.

Hasta ahora, nuestro entendimiento básico de los grupos ha demostrado ser lo suficientemente útil para diseñar esquemas criptográficos que se adaptan a muchas necesidades — cifrado, firmas, (y algunas variantes exóticas), pruebas, compromisos, aleatoriedad verificable, etc.

Creo que es el momento adecuado para profundizar un poco más en nuestra comprensión de las estructuras de grupo y, al hacerlo, descubrir un nuevo conjunto de primitivas criptográficas geniales.

Es posible que ya hayas oído hablar de homomorfismos e isomorfismos. Pero, ¿qué son estas cosas con nombres tan peculiares?

Homomorfismos en Pocas Palabras

En general, un homomorfismo es una función o mapeo que preserva propiedades algebraicas.

Recuerda que cuando trabajamos con grupos, solo tenemos un conjunto y una operación. Así que un homomorfismo de grupo realmente mapea elementos de un grupo a otro grupo, donde las propiedades de la operación se preservan.

Todo este trabalenguas se puede reducir a esto: si a y b son elementos de un grupo, entonces un homomorfismo f debería comportarse así:

$$f(a + b) = f(a) + f(b)$$

Un gran ejemplo de homomorfismo ocurre cuando tomamos un grupo de una curva elíptica con generador $G$ y orden $n$, y el grupo aditivo de enteros módulo $n$. Y simplemente definimos:

$$f: \mathbb{Z}_n \rightarrow \langle G \rangle \ / \ f(x) = [x]G$$

Podemos ver fácilmente que la adición se preserva:

$$f(a) + f(b) = [a]G + [b]G = [a + b]G = f(a + b)$$

Isomorfismos

Observa que en el caso anterior, hay una correspondencia uno a uno entre los elementos de ambos grupos. Esto no tiene que ser siempre el caso: si hubiéramos elegido los enteros módulo $q$ en su lugar, con $q > n$, entonces al menos dos enteros compartirían el mismo valor funcional.

En el caso de que exista una correspondencia uno a uno, entonces en teoría podríamos usar $f$ para mapear $\mathbb{Z}_n$ a $\langle G \rangle$, y su inversa $f^{-1}$ para mapear $\langle G \rangle$ a $\mathbb{Z}_n$.

En términos matemáticos, esto significa que f es una biyección. Ya sabes, ¡por si quieres ser más preciso al respecto!

Cuando esto sucede, decimos que $f$ es un isomorfismo en lugar de un homomorfismo. Y se dice que los grupos son isomórficos.

Por lo que nos importa en términos de teoría de grupos, los grupos isomórficos son esencialmente el mismo grupo disfrazado, ya que podemos encontrar una función que nos permita transformar un grupo en el otro, y viceversa.

¿Por Qué Debería Importarme?

Ah, la pregunta del millón.

La idea de que los grupos sean homomórficos o isomórficos es muy interesante, porque moverse de un lado a otro entre los grupos elegidos significa que podemos realizar operaciones en cualquiera de ellos. Y esto nos permite hacer algo de magia. Veremos eso en acción en un minuto.

Antes de saltar a un ejemplo, quiero aclarar algunas notaciones que podrías encontrar. Si revisas, por ejemplo, esta página sobre el criptosistema de ElGamal (un algoritmo que veremos en un momento), notarás que no parecen usar adición al trabajar con grupos. En su lugar, usan multiplicación y notación exponencial:

$$y = g^x$$

Hmm. Esto no se parece a nuestros ejemplos anteriores. ¿Cómo es eso?

La clave para entender esto es ver las cosas bajo el lente del isomorfismo. Echa un vistazo a estos dos grupos:

$$\mathbb{Z}_5 = \{0, 1, 2, 3, 4\}$$ $$G_5 = \{1, g, g^2, g^3, g^4\}$$

Si simplemente tomamos papel y lápiz y hacemos coincidir elemento por elemento, podemos ver claramente que hay una correspondencia uno a uno. Formalmente, la relación tiene la forma:

$$f(x) = g^x$$

Decimos que el segundo grupo es multiplicativo — nota que la suma de elementos en $\mathbb{Z}_5$ se reemplaza por la multiplicación de elementos en $G_5$:

$$f(a + b) = g^{a+b} = g^a.g^b = f(a).f(b)$$

Esto es totalmente aceptable, ya que las operaciones en ambos grupos no son necesariamente las mismas.

Así que sí, si alguna vez ves la notación multiplicativa mientras miras un sistema basado en grupos, ten en cuenta que probablemente también se pueda formular una versión aditiva mediante este isomorfismo.

Encriptación Homomórfica

Bien, suficientes formalismos. Vamos a lo bueno.

Supongamos que quieres realizar una suma de dos enteros, módulo $q$. Pero estos números están encriptados o cifrados. Normalmente, tendrías que desencriptar ambos números y sumarlos. Y si quieres almacenar el resultado encriptado, tendrías que volver a encriptar.

Pero, ¿qué pasaría si pudiéramos saltarnos la desencripción por completo?

Este es exactamente el objetivo del encriptación homomórfica: realizar operaciones con datos protegidos y privados, pero obteniendo el mismo resultado que si operáramos con los datos en texto plano y sin protección, y luego los encriptáramos.

Click to zoom

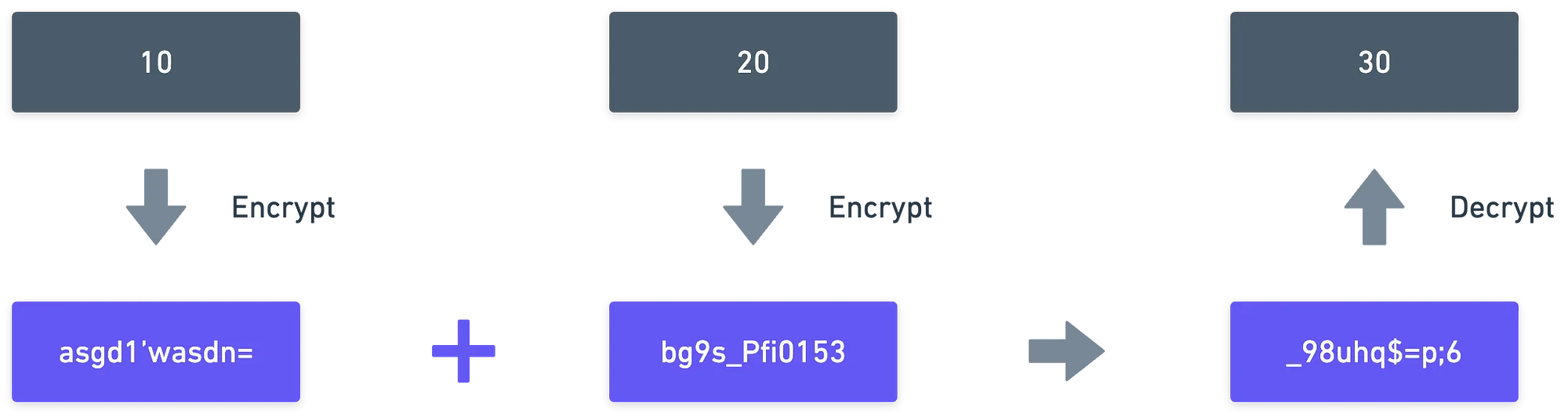
Y eso es genial, porque podemos ahorrarnos el tiempo de ejecutar operaciones de desencripción — que son costosas —, mientras preservamos la privacidad de los datos.

En teoría, al menos. Hay algunos matices en torno a esto, como discutiremos en un minuto. Pero la parte de privacidad es genial, ¡eso sí!

Entonces, ¿cómo logramos este tipo de funcionalidad?

Cifrado ElGamal

Este es uno de los criptosistemas más simples que existen. A pesar de su simplicidad, la función de cifrado o encriptación tiene una propiedad muy agradable: ¡es homomórfica!

Por lo tanto, podemos realizar operaciones con los datos cifrados. Veamos cómo funciona.

Como siempre, comenzaremos con Alicia teniendo una clave privada $d$, que usa para calcular una clave pública $Q = [d]G$. Y sí, $G$ es tu típico generador de curva elíptica.

Digamos que Bruno quiere cifrar un mensaje para Alicia, conociendo su clave pública $Q$. Para que esto funcione, debemos asumir que el mensaje es un punto en la curva elíptica, $M$. Y esto se puede obtener pasando el mensaje original a través de una función reversible (el hashing no servirá).

No cubriremos cómo hacer ese primer paso ahora — asumamos simplemente que sabemos cómo hacerlo.

Entonces, Bruno sigue este procedimiento para cifrar:

• Elige un entero aleatorio r, y calcula $R = [r]G$.
• Después, calcula una máscara (como siempre) como $[r]Q$.
• Finalmente, agrega la máscara al mensaje, así $C = M + [r]Q$.

El texto cifrado obtenido es $(R, C)$. Para descifrar, Alicia tiene que:

• Calcular $[d]R$, que será exactamente igual a la máscara $[r]Q$.
• Restar la máscara de $C$, así $C - [r]Q = M$.

Ya que estamos siendo más precisos ahora, podemos decir que restar es realmente agregar el inverso aditivo del valor restado. Es solo más fácil decir "restar".

La parte de cifrado de este proceso se puede expresar como una función que toma un mensaje $M$ y algo de aleatoriedad $r$, y produce un texto cifrado:

$$\varepsilon: \langle G \rangle \times \mathbb{Z}_q \rightarrow \langle G \rangle \times \langle G \rangle \ / \ \varepsilon(M,r) = ([r]G, M + [r]Q)$$

Y este será nuestro homomorfismo.

Imagina que cifras $M_1$ con aleatoriedad $r_1$, y $M_2$ con aleatoriedad $r_2$. ¿Qué sucede si sumamos los resultados cifrados?

$$\varepsilon(M_1, r_1) + \varepsilon(M_2, r_2) = ([r_1]G, M_1+[r_1]Q) + ([r_2]G, M_2+[r_2]Q)$$ $$= ([r_1 + r_2]G, M_1+M_2+[r_1 + r_2]Q) = \varepsilon(M_1 + M_2, r_1 + r_2)$$

¡Y boom! ¡El resultado es el mismo que si hubiéramos sumado primero los mensajes (y la aleatoriedad)!

Como por arte de magia.

Observaciones

El esquema presentado anteriormente es tan simple como puede ser. Y aunque este ejemplo es muy ilustrativo, no es perfecto de ninguna manera, y hay una o dos cosas que debemos decir al respecto.

Mensajes Codificables

Primero, nota que el mensaje que podemos encriptar está relacionado con el orden del grupo, $n$. Recuerda que el orden del grupo significa el número de elementos en el grupo, por lo que solo hay un número finito (exactamente $n$) de puntos diferentes en el grupo.

Como se requiere codificar reversiblemente nuestro mensaje a un punto $M$, entonces esto significa que cada punto $M$ corresponde a un mensaje único, por lo que solo hay $n$ mensajes únicos que podemos codificar.

Y esto, a su vez, significa que no podemos codificar un mensaje de longitud arbitraria. Podríamos pensar en estrategias ingeniosas para separar un mensaje en "trozos", pero esto podría socavar el aspecto homomórfico de nuestro esquema.

Pero esto no significa que la técnica no tenga valor — por ejemplo, piensa en los mensajes como saldos privados. Podríamos manejar un saldo máximo representable, ¿no es así?

Homomorfismo Parcial

Por otro lado, este cifrado homomórfico solo admite una operación. Y esto es de esperarse, ya que estamos trabajando con grupos. Así que si la operación del grupo es la suma, entonces no podemos hacer multiplicación. Y por lo tanto, esto se conoce como Cifrado Parcialmente Homomórfico, o PHE (por sus siglas en inglés).

Si pudiéramos soportar tanto la suma como la multiplicación, entonces nuestro esquema sería completamente homomórfico — y hablaríamos de Encriptación Completamente Homomórfica, o FHE (Fully Homomorphic Encryption) por sus siglas en inglés.

Crear un esquema de cifrado completamente homomórfico no es tarea fácil — y los grupos simplemente no servirán. Necesitaremos una estructura matemática diferente para abordar esto, una que soporte dos operaciones. Cuando ese es nuestro requisito, necesitamos adentrarnos en el dominio de la teoría de anillos, un esfuerzo que emprenderemos más adelante en la serie.

Pruebas de Conocimiento Cero

Imagina una aplicación con saldos privados. Puedes descifrar tu propio saldo, pero quien procesa una solicitud de transferencia no puede. Por lo tanto, necesitas probar de alguna manera al procesador que:

• Conoces tu saldo y la cantidad a transferir
• Tienes suficiente saldo para cubrir la transferencia

¡Pero necesitas hacer esto sin revelar los valores, porque el objetivo principal de la aplicación es mantener los saldos privados!

Para hacer esto, necesitaremos combinar nuestros esfuerzos de cifrado homomórfico con Pruebas de Conocimiento Cero (ZKPs por sus siglas en inglés). Y generalmente hablando, las ZKPs tienden a ser computacionalmente costosas — por lo que los beneficios de no tener que descifrar se equilibran de alguna manera debido a esto. Sin embargo, puede ser necesaria la privacidad de los datos — por ejemplo, la encriptación homomórfica es una solución atractiva para la privacidad en redes públicas, como las Blockchains.

Resumen

En esta ocasión, profundizamos un poco más en las matemáticas, lo que en última instancia nos permite comprender mejor las estructuras que subyacen a nuestras construcciones.

Vimos un esquema de encriptación (parcialmente) homomórfico en acción. Por supuesto, el de ElGamal no es el único sistema que tiene esta propiedad de homomorfismo. Existen otros esquemas basados en grupos, como el criptosistema de Benaloh o el muy citado criptosistema de Paillier.

Hemos recorrido un largo camino. Por ahora, pondremos fin a nuestra exploración de la criptografía de curvas elípticas (ECC). Pero este no es el final del viaje, de ninguna manera. Resulta que los grupos de curvas elípticas funcionan muy bien con otra construcción que permite criptografía muy interesante. Entraremos en eso pronto.

Sin embargo, hay un tema que quiero abordar antes: polinomios y las posibilidades que ofrecen. ¡Este será el tema del próximo artículo!