Criptografía 101: Circuitos Aritméticos

Este artículo forma parte de una serie más larga sobre criptografía. Si este es el primer artículo con el que te encuentras, te recomiendo encarecidamente comenzar desde el principio de la serie.

La última vez, nos sumergimos bastante profundo en un ejemplo particular de un protocolo de prueba de conocimiento cero. Dejando de lado las optimizaciones y cuestiones de rendimiento, cubrió el caso de uso deseado: probar que un número está en un cierto rango. Sin embargo, el protocolo era tremendamente específico, y crear otro protocolo para otra afirmación requiere investigación dedicada, probablemente resultando en una secuencia completamente diferente de pasos.

Concluimos diciendo que un marco general para pruebas de conocimiento cero podría ser una empresa interesante a seguir.

¡Y llegaremos allí — solo que no ahora mismo!

El plan para hoy es presentar algunos fundamentos sobre los cuales construiremos inmediatamente después, en el próximo artículo.

Ya que hablamos de bits en nuestro encuentro anterior, tomemos un pequeño desvío y revisemos brevemente sus usos. ¿De acuerdo?

Circuitos Binarios

Es probable que si estás leyendo esto, estés al menos algo interesado en las computadoras, así que hablemos de eso.

El hecho de que el bit sea la unidad básica para la representación de datos en la ciencia de la computación está estrechamente relacionado con cómo funcionan las computadoras. En términos simples, la corriente eléctrica que fluye a través de un circuito puede considerarse un uno ($1$), mientras que el estado donde no fluye corriente eléctrica a través del mismo circuito puede representar un cero ($0$). Y, de hecho, estas corrientes son cómo se representan los bits en el mundo físico.

Pero las computadoras no serían tan geniales como son si no pudiéramos realizar algunas operaciones con dichos datos.

Lo primero que podemos hacer es combinar dos bits (recuerda, son solo señales eléctricas), de varias maneras. Por ejemplo, podríamos crear una caja que solo genere $1$ cuando ambas entradas de señal también son $1$, y $0$ en caso contrario:

Click to zoom

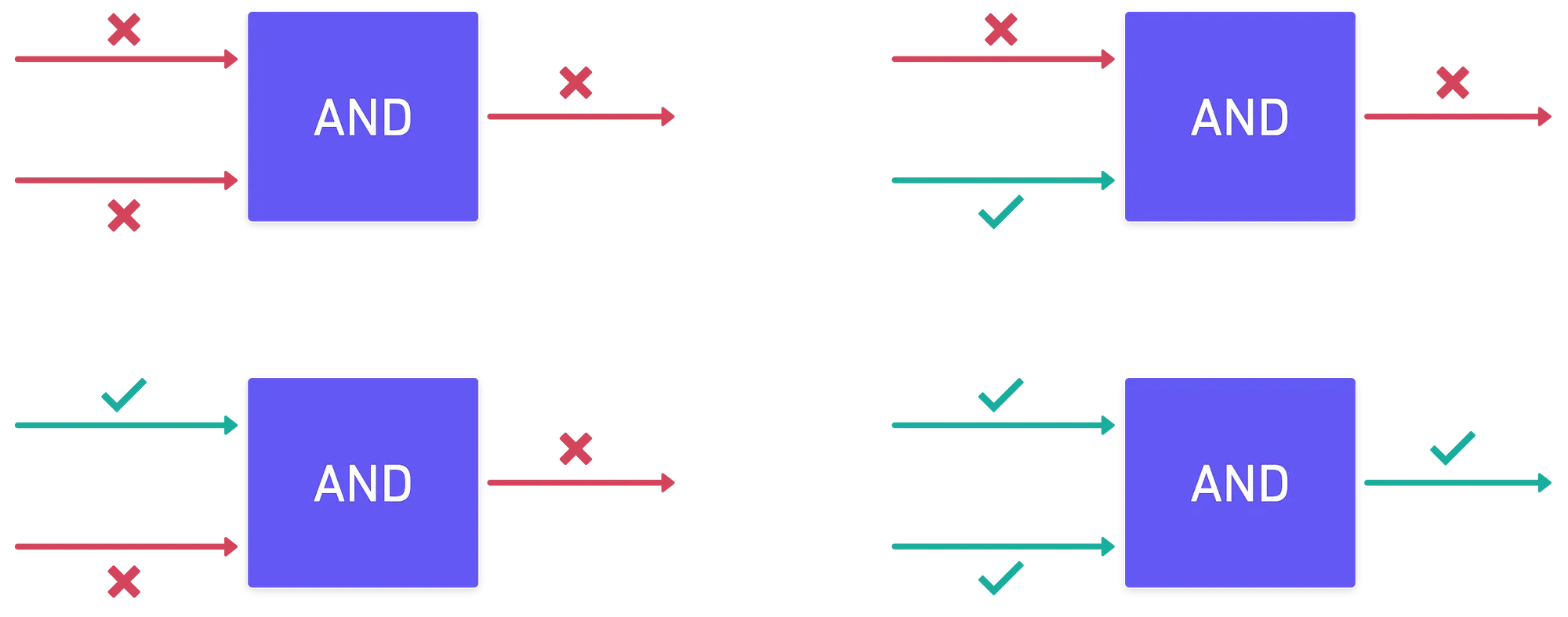
Este tipo de cajas se llaman compuertas lógicas, y son las que permiten a las computadoras hacer su magia. Existen otras compuertas simples, como $\textrm{NOT}$, $\textrm{OR}$, $\textrm{XOR}$, $\textrm{NAND}$, $\textrm{NOR}$ y $\textrm{XNOR}$ — todas ellas siendo disposiciones ingeniosas de circuitos eléctricos.

Click to zoom

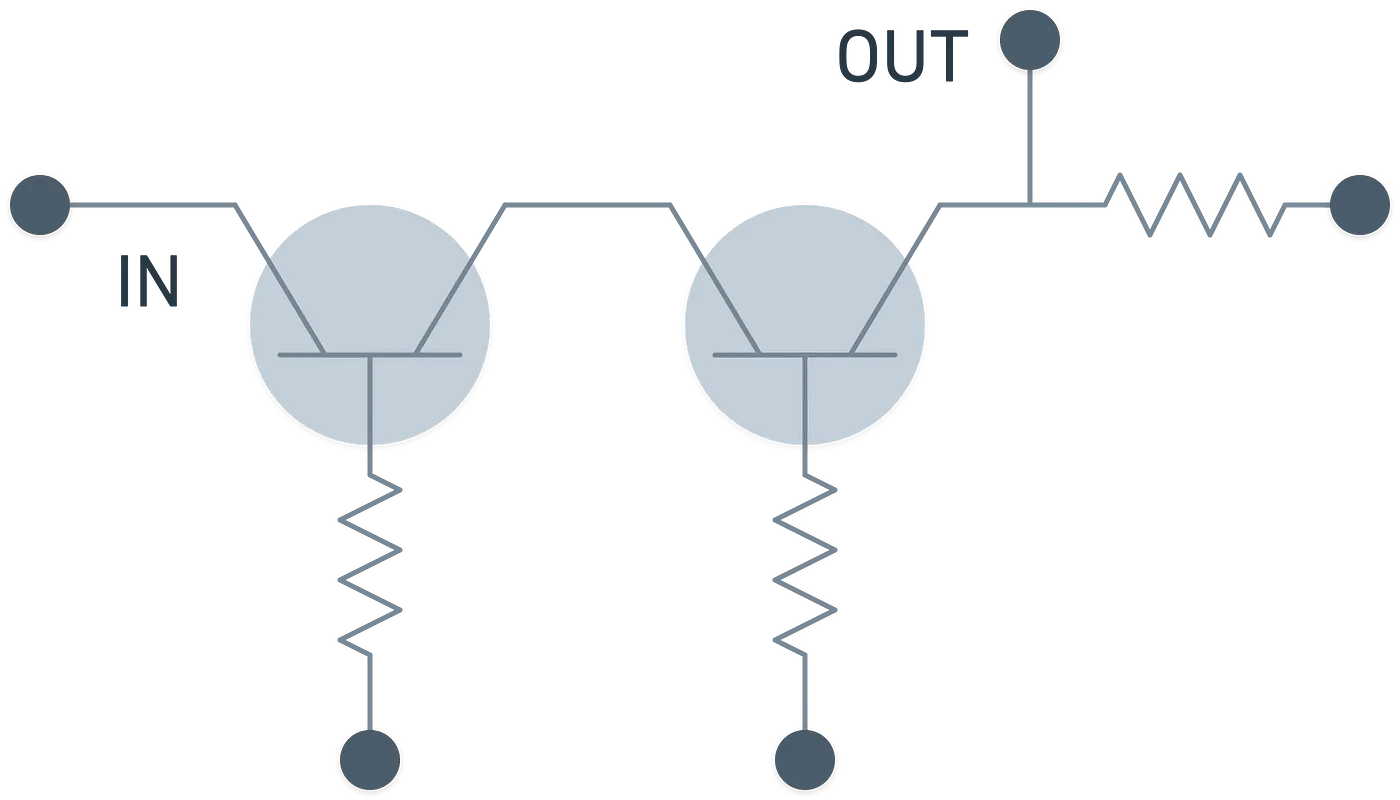
Dos señales todavía es muy poco — podemos hacerlo mejor. Así que podemos procesar múltiples entradas colocando algunas compuertas y obteniendo una serie de salidas en el proceso. La forma en que se disponen las compuertas se llama circuito, que es esencialmente un modelo para computación.

Por ejemplo, podemos sumar dos números de dos bits $A = (a_0, a_1)$ y $B = (b_0, b_1)$ con este circuito bastante simple:

Click to zoom

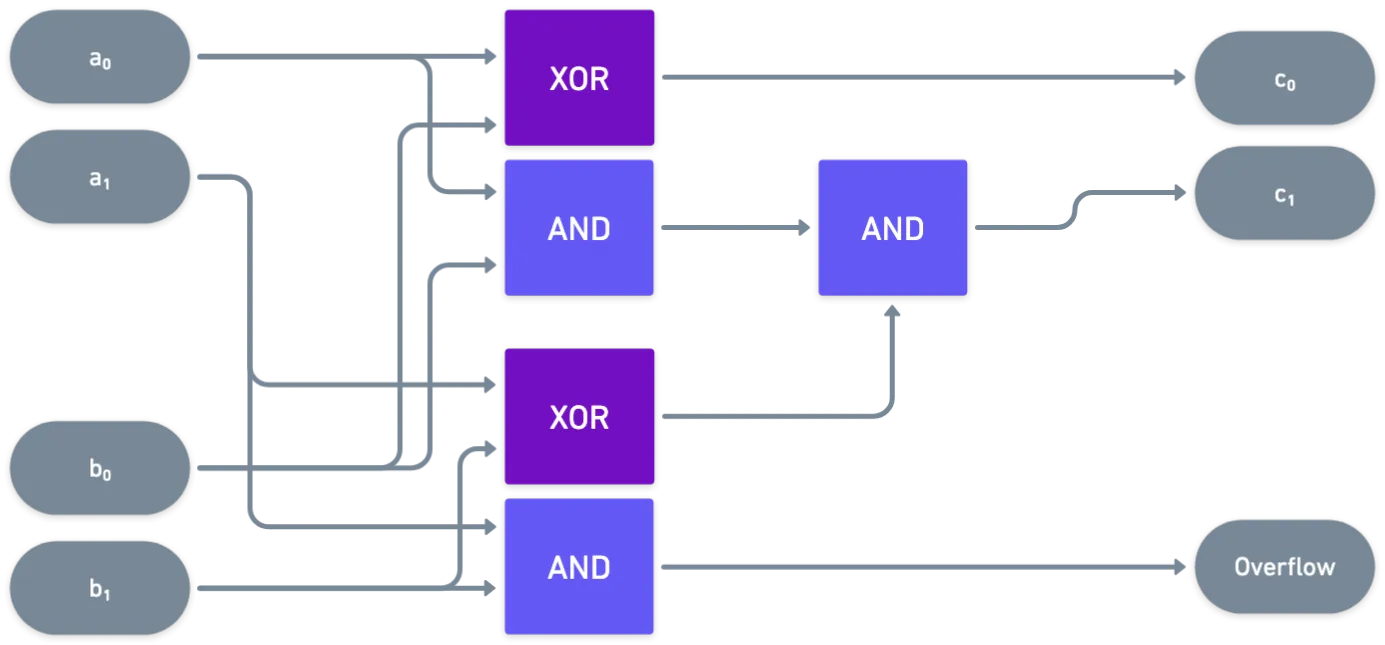
Se pueden crear todo tipo de circuitos para todo tipo de propósitos usando múltiples compuertas y manejando múltiples entradas.

Cambiando Perspectivas

Veamos estos circuitos binarios desde otra perspectiva. Un bit es simplemente un número que pertenece al conjunto $\{0,1\}$. Y este conjunto también funciona como un campo finito: la suma, multiplicación, resta y división (excepto por $0$) están todas definidas. Usamos la operación módulo para que nos mantengamos en rango — por ejemplo, $1 + 1 \ \textrm{mod} \ 2 = 0$.

En este sentido, podríamos pensar en las compuertas como operaciones matemáticas sobre dicho campo finito. Una compuerta $\textrm{XOR}$ representa correctamente la suma módulo $2$, mientras que una compuerta $\textrm{AND}$ representa la multiplicación módulo $2$:

Click to zoom

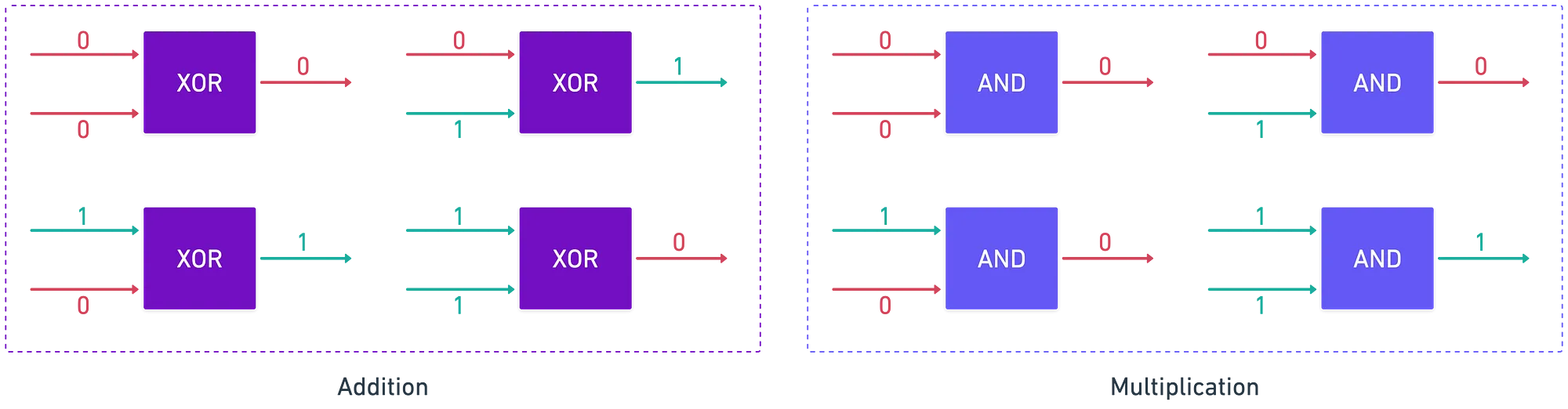
Bien, genial... ¿Y ahora qué?

Digamos que etiquetamos las entradas como $x$ e $y$. Agreguemos también $1$ como entrada, para mayor seguridad. ¿Qué sucede si configuramos algunas compuertas?

Click to zoom

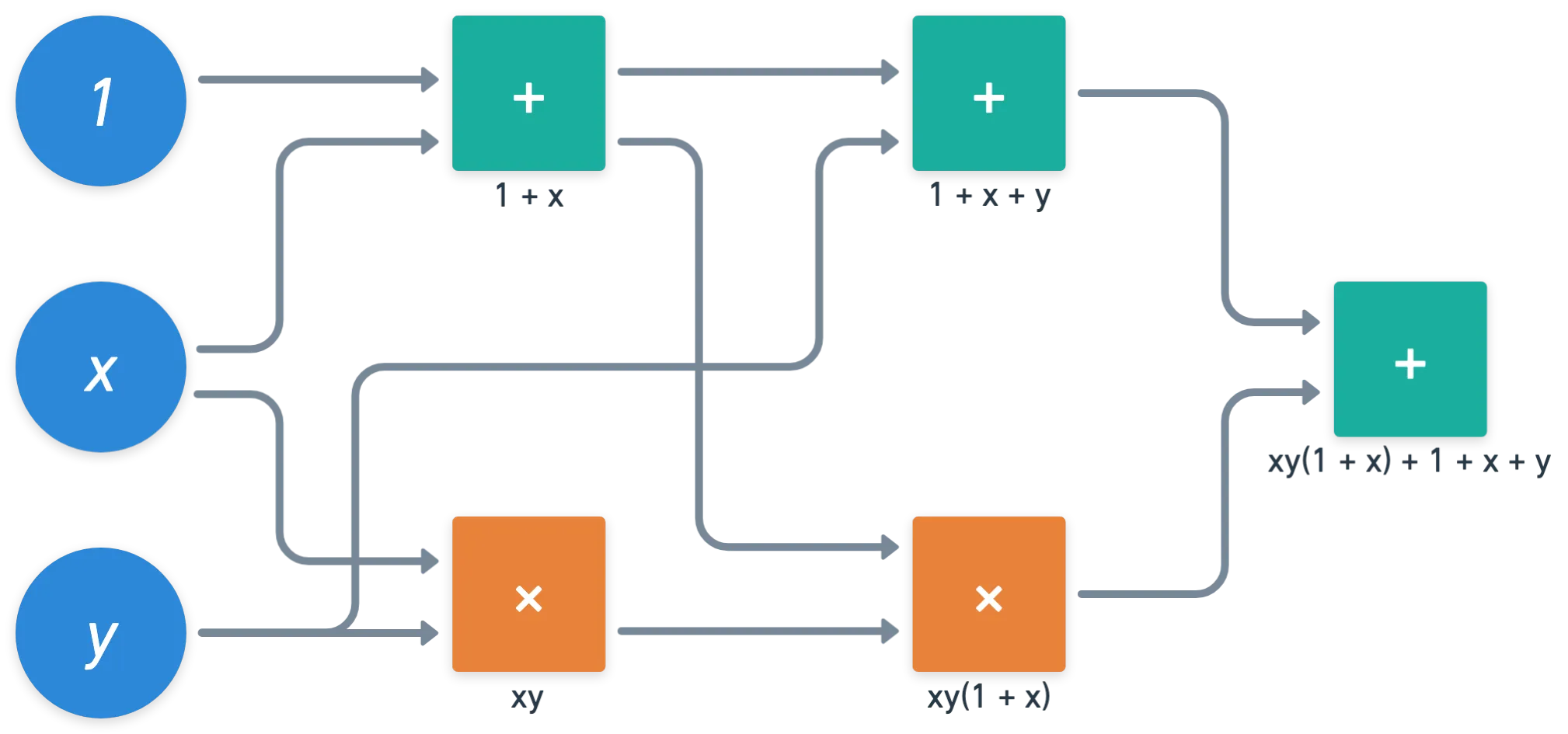
¿Qué es eso en la salida? ¿Es... Un polinomio? ¡Bien!

Básicamente, podemos representar un polinomio binario con solo un montón de compuertas de suma y multiplicación. De hecho, es una prescripción sobre cómo calcular el polinomio en sí mismo, paso a paso.

Y ya sabemos que los polinomios tienen bastantes aplicaciones en criptografía. Así que aquí va una idea: ¿por qué limitarnos al módulo $2$? ¿Qué nos impide extender esta receta para computación a cualquier campo finito arbitrario?

Circuitos Aritméticos

Para un campo finito con $q$ elementos (por ejemplo, los enteros módulo $q$), podemos usar el mismo tipo de circuito para prescribir el cálculo polinómico. La única diferencia con el circuito anterior es que todas las operaciones se realizan módulo $q$ en lugar de módulo $2$, ¡pero eso es toda la diferencia!

Click to zoom

Formalmente, esto se conoce como un circuito aritmético. Es solo un grafo, que mapea entradas a nodos (llamados compuertas) que representan operaciones binarias (aquí, binario significa que cada compuerta toma dos entradas).

En su versión más simple, las únicas compuertas que se utilizan son suma y multiplicación. Estas operaciones simples son realmente económicas de ejecutar — lo que hace que este sea un buen modelo de cálculo en entornos con recursos limitados, como las Blockchains.

Por cierto, es importante que el circuito sea un grafo acíclico dirigido (DAG), para que el cálculo solo se realice hacia adelante, obteniendo así un resultado único.

¿Por Qué la Molestia?

En este punto, podrías estar preguntándote "¿por qué definir un grafo y demás, si puedes calcular el polinomio directamente?". Es decir, si tienes la fórmula y los coeficientes... ¿Por qué no simplemente hacer los cálculos directamente, y olvidarse del circuito?

Aunque esto es justo, hay algunas consideraciones que hacer — sobre descomponibilidad, paralelismo, generalidad, etc. Veremos esto en acción más adelante.

Por ejemplo, en protocolos homomórficos, uno podría desear realizar operaciones que se sabe que preservan la estructura algebraica. Y tales operaciones suelen ser la suma y multiplicación "simples" — descomponer un polinomio en sus pasos simples puede entonces ayudar a preservar las propiedades algebraicas y, por lo tanto, permitir que los protocolos homomórficos admitan cálculos complejos.

Aplicación

Los circuitos aritméticos son otra herramienta a nuestra disposición. Pero como siempre, las herramientas no valen mucho si no tienen aplicación.

Avanzando, quiero centrarme en un aspecto que es de particular interés para las pruebas de conocimiento cero. Y para hacer esto, juguemos al Sudoku.

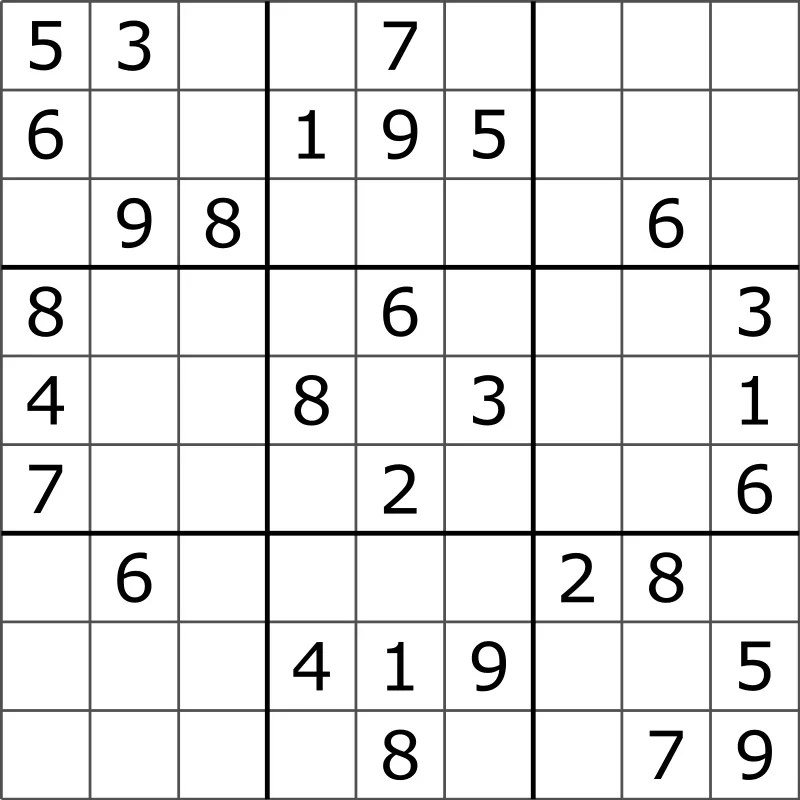
Resolver un viejo y querido Sudoku normalmente no es tan difícil (¡aunque a veces puede volverse bastante desafiante!). Lo que seguramente es más fácil es comprobar si una solución dada es válida — ya sabes, siempre que no haya números repetidos en cada fila, columna y caja cuadrada, estamos bien.

Pero ustedes están pensando en el Sudoku "estándar", que es una cuadrícula de $9 \times 9$. El juego podría expandirse usando una cuadrícula más grande, algo como $16 \times 16$, $25 \times 25$, $100 \times 100$, y así sucesivamente. A medida que la cuadrícula crece en tamaño, el problema se vuelve mucho, mucho más difícil. Sin embargo, comprobar una solución válida sigue siendo fácil: todavía verificas que no haya números repetidos en cada fila, columna y caja cuadrada.

Esto alude al hecho de que a veces, verificar la solución de un problema es mucho más fácil que encontrarla — y esto, podemos usarlo a nuestro favor.

Si estás interesado en el tema, es posible que ya hayas oído esto citado como un ejemplo del problema P vs NP. Realmente, no se ha demostrado que los problemas que son difíciles de resolver y fáciles de verificar realmente existan — es decir, no se ha demostrado matemáticamente que es más difícil resolver un sudoku gigante que verificarlo.

Y esto es tan fundamental para la ciencia de la computación, que hay una recompensa de un millón de dólares para cualquiera que demuestre si P = NP o no.

Sí, es así de importante.

Comprobando la Solución

La verificación, como se mencionó anteriormente, ocurre comprobando que los números no se repiten. ¿Qué tal si intentamos escribir esto en forma de ecuaciones?

Si los números no deben repetirse, esto significa que cada fila, columna y cuadrado deben sumar el mismo número, $S$:

$$S = \sum_{i=1}^n i$$

Y creo que nadie se quejará si represento los valores de un Sudoku como una matriz — quiero decir, ¡incluso es un cuadrado! Servido en bandeja para nosotros.

$$\begin{bmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n^2}\\ a_{2,1} & \ddots & & \vdots \\ \vdots & & \ddots & \vdots \\ a_{n^2,1} & \cdots & \cdots & a_{n^2,n^2} \\ \end{bmatrix}$$

Algunos de estos valores son, por supuesto, prescritos, ya que el rompecabezas necesita un estado inicial para que tenga una única solución.

Concentrémonos por un segundo en la columna $1$. Si sumamos todos los elementos, una solución válida debería dar el valor esperado $S$:

$$S = \sum_{i=1}^n a_{i,1}$$

Por supuesto, tenemos que escribir el mismo tipo de verificación para cada fila, columna y cuadrado — dando un gran total de $3n$ ecuaciones. Incluso si una sola de esas verificaciones falla, entonces inmediatamente sabemos que la solución no es válida.

¡Y estas ecuaciones pueden representarse como un circuito aritmético muy simple! Solo, tal vez, con bastantes compuertas de suma.

Click to zoom

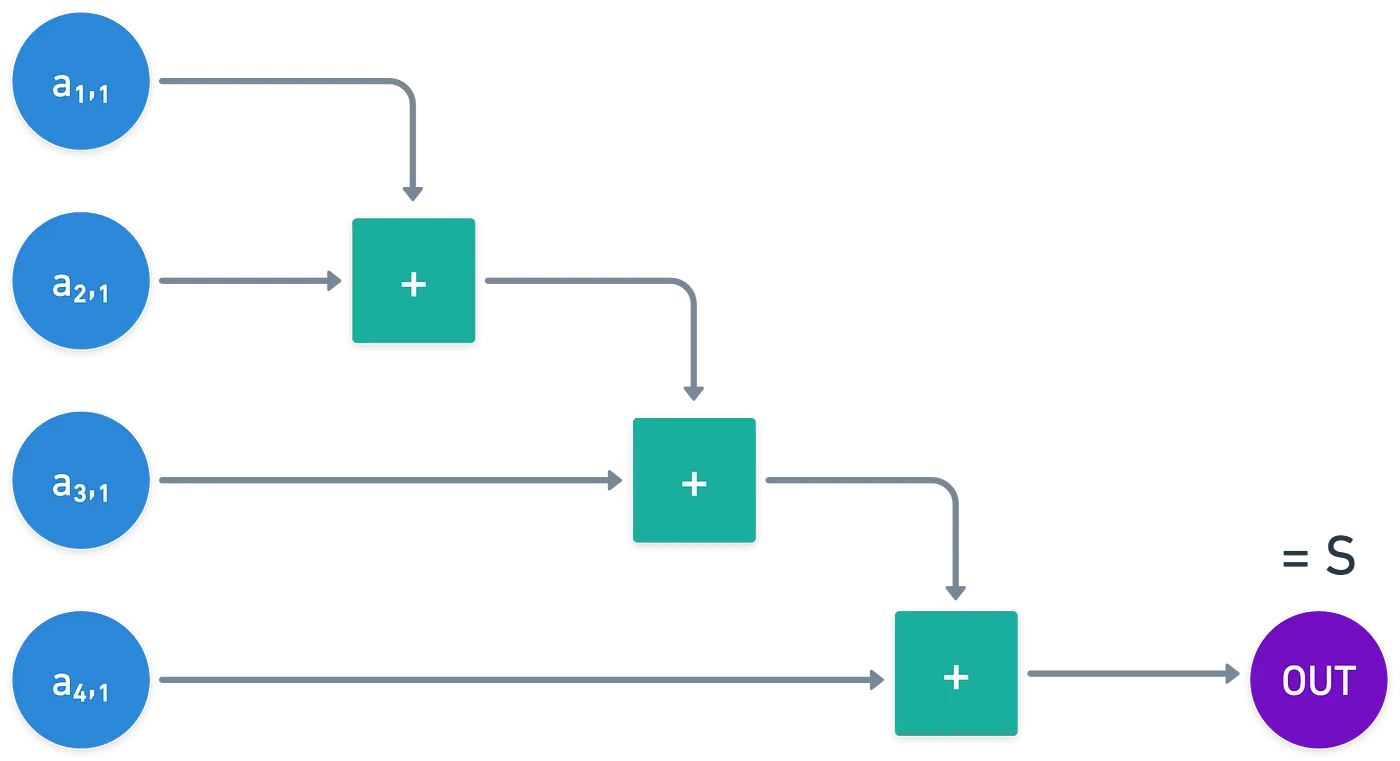
Ahora tenemos un modelo de cálculo general para la verificación de una solución a un problema. En otras palabras, conocimiento de una solución. Así, cuando trabajamos con pruebas de conocimiento, podríamos construir un circuito que represente la verificación de una solución a un problema de elección.

Dicho problema podría ayudarnos a probar una miríada de afirmaciones: que un número está en un rango dado, que conocemos algún logaritmo discreto, que conocemos el hash de un valor — realmente, muchas afirmaciones. ¡Y esto es lo que da a los circuitos aritméticos su flexibilidad!

Una Nota sobre Conocimiento Cero

¡Fantástico! Ahora sabemos que dada alguna afirmación, podemos crear un circuito aritmético para representar su verificación. Excepto que la verificación requiere las entradas al circuito.

En pruebas de conocimiento cero, nos gustaría evitar revelar dichas entradas (o al menos, las que deberían ser privadas). Entonces, ¿qué hacemos? ¿Hemos introducido circuitos aritméticos para nada?

No te preocupes, querido amigo — no fue en vano.

Debido a que los circuitos aritméticos pueden ser descompuestos en elementos simples (sus compuertas), podemos hacer algo de magia que permitirá a un verificador comprobar un cálculo válido sin conocimiento de las entradas elegidas. ¡Llegaremos a eso pronto!

Resumen

Este artículo presentó la noción de circuitos aritméticos y su papel como modelo de cálculo general. En este sentido, discutimos cómo pueden usarse para verificar soluciones a un problema — siendo que el problema está correctamente representado por el circuito aritmético.

Los circuitos aritméticos son modelos generales para cálculos que se descomponen fácilmente en sus bloques de construcción: las compuertas.

Y mencionamos cómo estos circuitos aritméticos pueden ser fácilmente descompuestos, y cómo esto ayudará en el aspecto "cero" de las pruebas de conocimiento cero. Sin embargo, esto involucrará algunas nuevas hazañas matemáticas.

Explicar esas hazañas, que finalmente nos llevarán a construir un protocolo de prueba de conocimiento cero, será el tema central del próximo artículo. ¡Hasta entonces!