Criptografía 101: Pruebas de Conocimiento Cero (Parte 2)
Este artículo forma parte de una serie más larga sobre criptografía. Si este es el primer artículo con el que te encuentras, te recomiendo encarecidamente comenzar desde el principio de la serie.
En los últimos artículos, hemos cubierto muchos bloques de construcción. Es hora de finalmente combinar todas estas piezas de lego en un protocolo. ¡Hurra!
Recuerda, la razón por la que hicimos tanto esfuerzo para entender estas partes móviles fue para tratar de construir un marco general para pruebas de conocimiento cero — porque, como vimos, crear un protocolo para una aplicación específica era algo poco práctico, requiriendo investigación específica.
Ahora estamos listos para introducir una familia de pruebas de conocimiento que utiliza cada elemento que hemos definido preventivamente: SNARKs.
Específicamente, veremos un esquema llamado Plonk. Para una divulgación completa de la técnica, ve aquí. Haré mi mejor esfuerzo para explicar esto con la mayor precisión posible. Además, este no es el único protocolo que califica como SNARK por ahí. Existen otros mecanismos como Groth16, Marlin y Halo. Podría abordar esos en el futuro, pero por ahora, ¡solo dejaré un par de enlaces aquí en caso de que quieras seguir tu curiosidad!
Advertencia
Este artículo va a ser largo, y honestamente, complejo. Es decir, probablemente más difícil de lo habitual. Hay un límite en lo que puedo hacer para simplificar la explicación de un protocolo que es bastante complejo.
Pero, si tuviera que resumir todo este proceso en una sola frase, sería:
![]()
![]() En Plonk, codificamos el cálculo de un circuito en una serie de polinomios, que representan las restricciones impuestas por el circuito, para los cuales podemos probar afirmaciones mediante una serie de pruebas, sin revelar jamás los polinomios mismos — y por lo tanto, sin filtrar las entradas secretas.
En Plonk, codificamos el cálculo de un circuito en una serie de polinomios, que representan las restricciones impuestas por el circuito, para los cuales podemos probar afirmaciones mediante una serie de pruebas, sin revelar jamás los polinomios mismos — y por lo tanto, sin filtrar las entradas secretas.![]()
![]()
Llegar a entender esto completamente será un viaje salvaje. Y hay varios elementos que necesitaremos cubrir. Aquí hay una visión general del plan, que también funciona como una especie de tabla de contenidos:
- Circuitos como conjuntos de restricciones
- Codificando el circuito en polinomios
- Listando los requisitos para la verificación
- Técnicas para la verificación
- Verificación
Además, estoy asumiendo que ya revisaste el artículo sobre esquemas de compromiso polinomial, y también el de circuitos aritméticos. Si no lo has hecho, ¡te recomiendo encarecidamente leerlos!
Sin más preámbulos, ¡aquí vamos!
¿Qué es un SNARK?
El acrónimo significa Succint Non-interactive ARguments of Knowledge (Argumentos de Conocimiento Sucintos No Interactivos). En español simple: un mecanismo para probar conocimiento de algo, que es sucinto (o corto, o pequeño) y no interactivo. Hay un par de cosas que necesitamos analizar aquí, para entender mejor el objetivo de la construcción:
- Sucinto significa que cualquier prueba que produzcamos debe ser pequeña en tamaño y rápida en tiempo de evaluación.
- No interactivo significa que al recibir la prueba, el verificador no necesitará más interacción con el probador. Más sobre esto más adelante.
- Finalmente, decimos que esta es una prueba de conocimiento, pero no necesariamente una prueba de conocimiento cero (aunque puede serlo). En particular, Plonk califica como conocimiento cero debido a cómo está construido.
No te preocupes — aún no podemos construir nuestro SNARK. Primero necesitaremos cubrir algunos conceptos.
Revisitando los Circuitos
En el artículo anterior, vimos cómo los circuitos aritméticos eran una buena manera de representar un cálculo. Y cómo permitían la elaboración de recetas para la validación de afirmaciones.
Y así, el objetivo del probador será tratar de convencer a un verificador de que conoce algún valor secreto — realmente, un vector de valores — tal que:
Esto se lee: "existe algún vector cuyos elementos están en el campo finito , tal que , donde es públicamente conocido.
El probador no quiere revelar , pero además, no queremos que el verificador ejecute el cálculo costoso del circuito. Y así, lo que realmente sucederá es que el probador evaluará el circuito, y luego de alguna manera codificará tanto las entradas como los resultados para cada una de las compuertas — también llamado el rastro de cálculo.
Aquí hay un ejemplo de evaluación, utilizando el campo :
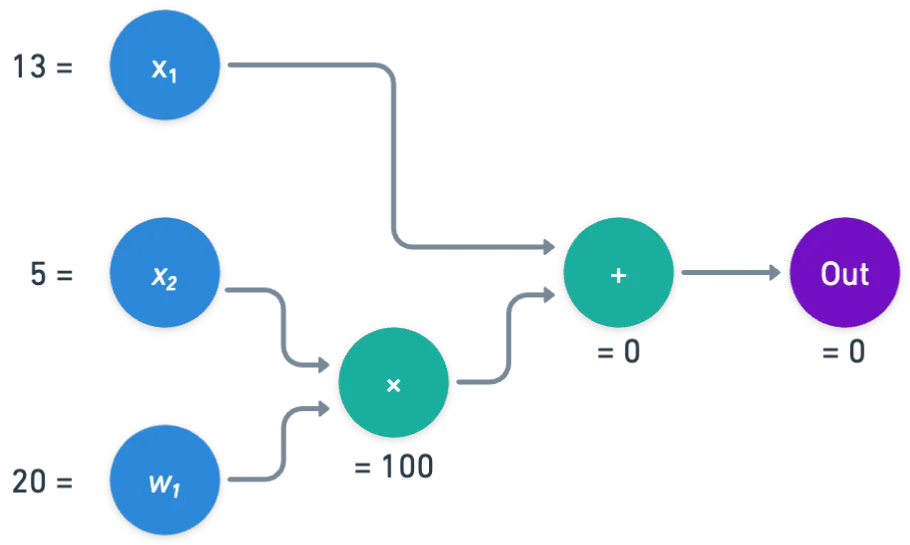
Y podríamos pensar en esta evaluación como el siguiente rastro, visualizado como una tabla:
| entradas | 20 | 13 | 5 |
| entrada izquierda | entrada derecha | salida | |
|---|---|---|---|
| compuerta 0 | 5 | 20 | 100 |
| compuerta 1 | 13 | 100 | 0 |
La fantástica idea detrás de los SNARKs modernos, incluido Plonk, es codificar este rastro como polinomios, lo que finalmente permitirá a un verificador comprobar que el cálculo es válido. Válido aquí significa que se sigue un conjunto específico de restricciones. Concretamente:
- Que cada compuerta se evalúa correctamente
- Que los cables con el mismo origen tienen el mismo valor
Por cable, me refiero a las conexiones entre compuertas, o conexiones desde entradas a compuertas, en el circuito. Podemos pensar en estos cables como portadores de los valores del circuito, en lugar de los nodos mismos:
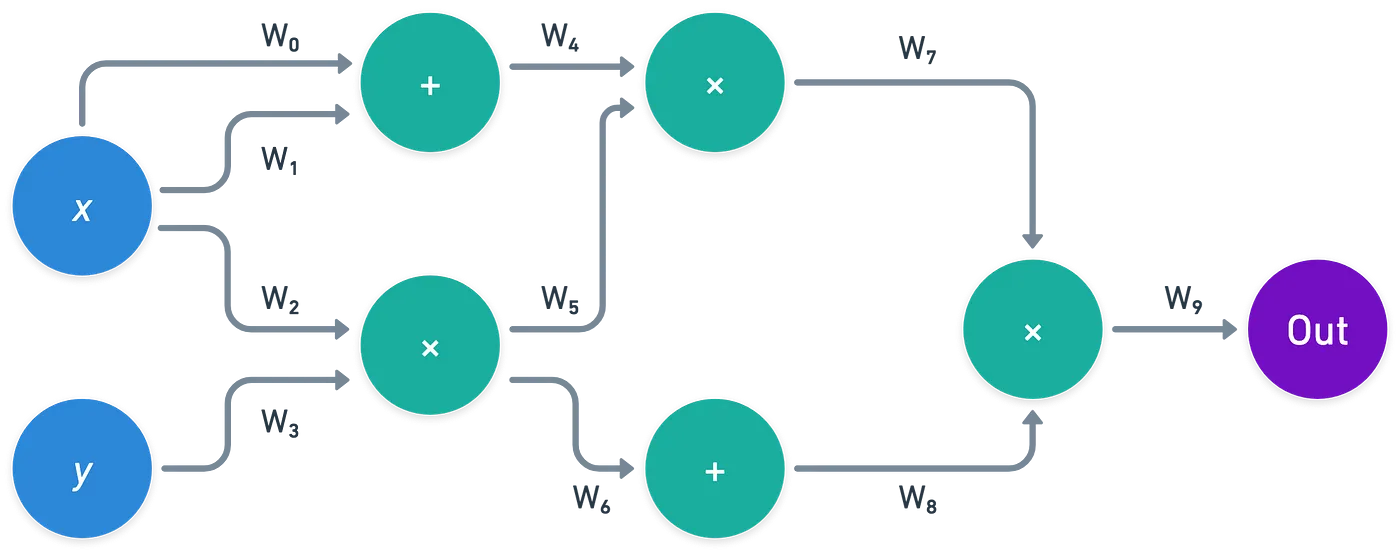
Aquí, puedes ver que algunos de estos cables deberían tener el mismo valor: , y — y también y . Además, las compuertas deberían tener sentido — lo que significa que, por ejemplo, debería ser igual a .
¡Un circuito puede ser una receta para el cálculo o un conjunto de restricciones para verificar!
Cada uno de estos conjuntos de restricciones — valores de cables, restricciones de compuertas y restricciones de cableado — se codificará en diferentes polinomios.
Por ejemplo, todo el rastro de cálculo puede codificarse en un solo polinomio , donde corresponde a un cable.
Tenemos los valores de los cables , pero necesitamos elegir a qué valores los codificamos. Usar algunos enteros es una opción perfectamente válida — ya sabes, el conjunto . Pero hay mucho que ganar usando las raíces de la unidad de nuestro campo en su lugar.

Raíces de la Unidad
Mencioné este concepto antes, pero evité tener que explicarlo más como Neo en Matrix.
Creo que ahora es un buen momento para ampliar un poco, para que podamos entender mejor la notación que viene más adelante.
Así que, sí, es hora de algunas definiciones. Llamamos a un valor (la letra griega omega) una raíz de la unidad -ésima del campo si:
En este caso, el conjunto :
también funciona como un grupo multiplicativo cíclico, generado por :
Hay dos cosas buenas sobre usar elementos de este conjunto como entradas a nuestro polinomio de codificación . Primero, pasar de una raíz de la unidad a la siguiente es tan simple como multiplicar por . Del mismo modo, moverse hacia atrás se hace multiplicando por el inverso de . Y da toda la vuelta - por definición:
En segundo lugar — y esta es la parte más importante — , usar este conjunto nos permite realizar interpolación utilizando el algoritmo más eficiente que conocemos: la Transformada Rápida de Fourier. No profundizaremos en cómo funciona (¡al menos no ahora!), pero debes saber que esto mejora el tiempo de interpolación dramáticamente — lo que significa que las pruebas son más rápidas de generar (que otros métodos de interpolación).
Codificando el Circuito
Habiendo dicho todo esto, es hora de ir al grano. Es momento de ver realmente cómo se codifica el rastro de cálculo.
Denotemos el número de entradas a nuestro circuito por , y el número de compuertas por . Con esto, definimos:
Cada compuerta tiene tres valores asociados: dos entradas y una salida. Y es por eso que usamos . Nota que este número mágico resulta ser exactamente el número de valores en el rastro de cálculo.
Codificaremos todos estos valores en las raíces de la unidad de orden :
Pero, ¿qué raíz codifica a qué cable? ¡Necesitamos un plan!
- Las entradas se codificarán usando potencias negativas de . Para la entrada , usamos:
- Los tres cables asociados a cada compuerta , ordenados como entrada izquierda, entrada derecha y salida, serán codificados por los siguientes valores:
Si miramos nuestro ejemplo de rastro, obtendríamos algo como esto:
Con esto, todos los valores en nuestro rastro de cálculo están incluidos en el polinomio. Solo tenemos que interpolar y obtener , que tendrá grado .
Codificación de Compuertas
Las compuertas presentan una complicación: pueden ser compuertas de suma o de multiplicación. Esto significa que probar que una compuerta se evalúa correctamente requiere que transmitamos información sobre su tipo.
Hacemos esto a través de un polinomio selector . Para la compuerta :
Cuando la compuerta es una compuerta de suma, entonces tomará el valor , y si es una compuerta de multiplicación, entonces tomará el valor . Para hacer esto simple de escribir, definamos:
Y luego construyamos la siguiente expresión:
No dejes que la expresión te asuste — lo que está sucediendo es en realidad bastante directo. Verás, ya sea o . Debido a esto, solo uno de los términos que contienen estará activo para alguna compuerta , y en consecuencia, esta expresión vincula entradas ( y ) y salidas (codificadas en ) de una compuerta, junto con el tipo de compuerta.
Codificación de Cableado
Esta es la más complicada de todas. Como se mencionó antes, puede suceder que algunos cables correspondan al mismo valor, ya que provienen de la misma fuente, como esto:
Lo que esto significa es que algunos de los valores codificados en necesitan coincidir:
Si analizamos el circuito completo, terminaremos teniendo un conjunto de este tipo de restricciones:
Esto es para el ejemplo anterior. Pero en general, las igualdades pueden tener más de miembros cada una
Cada una de estas debe ser codificada de alguna manera, por supuesto, en polinomios. La forma en que hacemos esto es bastante interesante: para cada restricción, definimos un polinomio que permuta o rota el subconjunto de raíces cuya evaluación debería coincidir. Así que por ejemplo, si la condición es:
Entonces definimos el subconjunto:
Y usando , creamos un polinomio que tiene el siguiente comportamiento:
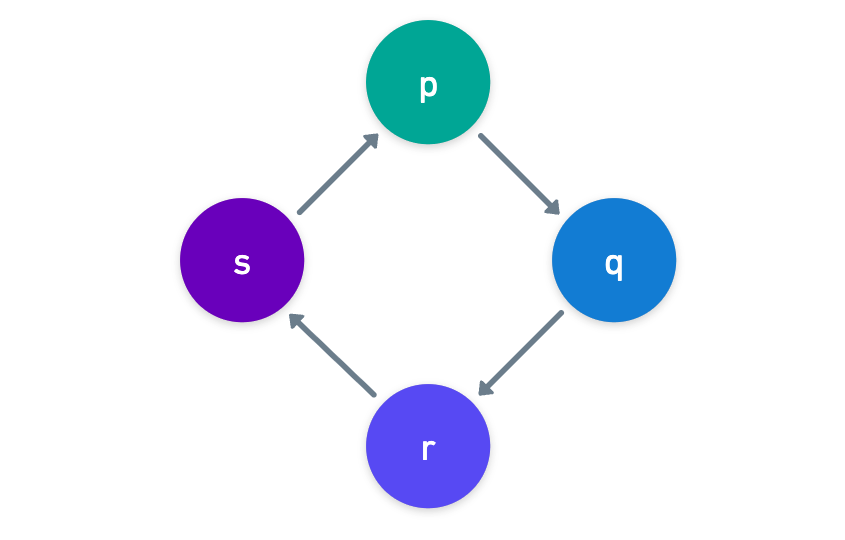
Debido a que siempre devuelve "el siguiente" elemento en , y dado que todos los valores de deberían ser iguales para las raíces en , la forma en que probamos que se cumple la restricción de cableado es probando que:
Esto debe hacerse para cada elemento en , cubriendo así todas las igualdades en una sola restricción.
¡Vaya! Eso fue ciertamente mucho. Sin embargo, ya hemos cubierto mucho terreno con esto.
En este punto, el probador tiene todos estos polinomios que codifican todo el rastro de cálculo. ¿Qué falta entonces? Solo la parte más importante: convencer a un verificador de que el rastro es correcto. Una vez que entendamos cómo sucede esto, finalmente todo estará unido.
Requisitos de Verificación
Por supuesto, el verificador no conoce los polinomios de los que acabamos de hablar. En particular, es crítico que nunca aprendan el completo. La razón de esto es que, si lo consiguen, entonces podrían fácilmente descubrir la información secreta , calculando:
¡La capacidad de nunca revelar estos valores mediante el uso de polinomios es lo que le da a Plonk sus propiedades de conocimiento cero!
Si el verificador no puede conocer los polinomios, entonces ¿cómo podemos convencerlos de algo? ¿Llegamos a un callejón sin salida? ¿Deberíamos entrar en pánico ahora?

Si bien el verificador no puede pedir los polinomios completos, seguramente puede pedir evaluaciones individuales de ellos. Deberían poder pedir cualquier valor de , o los — lo que significa que deberían poder consultar cualquier parte del rastro de cálculo. Excepto las entradas secretas, por supuesto.
Es en este punto donde nuestro PCS elegido resulta útil: cuando se solicita el valor de en algún punto (así, ), ¡el verificador puede comprobar que está correctamente calculado verificándolo contra un compromiso! Bieeeen.
¿Por qué harían eso, sin embargo? ¡Para comprobar que se mantienen las restricciones, eso es!
Para estar convencido de que el rastro de cálculo es correcto, el verificador necesita comprobar que:
- La salida de la última compuerta es exactamente (esto es una convención),
- Las entradas (las públicas, o el testigo) están correctamente codificadas,
- La evaluación de cada compuerta es correcta (ya sea que se cumpla la suma o la multiplicación),
- El cableado es correcto.
El primero es fácil — el verificador solo pide la salida en la última compuerta, que es:
Para las otras comprobaciones, sin embargo, necesitaremos agregar algo de magia (como de costumbre, a estas alturas).

Los Últimos Toques de Criptomagia
Tendremos que desviarnos un poco por un momento. Aquí hay una pregunta: dado algún polinomio de grado a lo sumo , y que no es idénticamente (así que ), ¿qué tan probable sería que para una entrada aleatoria (muestreada de los enteros módulo ), obtengamos que ?
Debido a que el polinomio tiene grado a lo sumo , tendrá a lo sumo raíces. Entonces, la probabilidad de que es exactamente la probabilidad de que resulte ser una raíz de :
Y siempre que sea suficientemente mayor que , entonces este es un valor despreciable (muy cercano a cero). Esto es importante: ¡si elegimos aleatoriamente algún y obtenemos que , entonces podemos decir con alta probabilidad que es idénticamente cero (la función cero)!
Esto se conoce como una prueba de cero. No parece ser mucho, pero vamos a necesitar esto para hacer funcionar nuestro SNARK.
Hay un par de comprobaciones más que podemos realizar, a saber, una comprobación de suma y una comprobación de producto. Esto ya es bastante información para digerir, así que omitamos esas por ahora.
Lo interesante es que existen Pruebas de Oráculo Interactivas eficientes para realizar estas pruebas.
Lo siento... Pruebas de QUÉ?

Pruebas de Oráculo Interactivas
¡Te advertí que esto no iba a ser fácil! Solo un poco más, y habremos terminado.
Las Pruebas de Oráculo Interactivas (IOPs, por sus siglas en inglés) son esencialmente una familia de mecanismos, mediante los cuales un probador y un verificador interactúan entre sí, para que el probador pueda convencer al verificador sobre la verdad de cierta afirmación. Algo como esto:
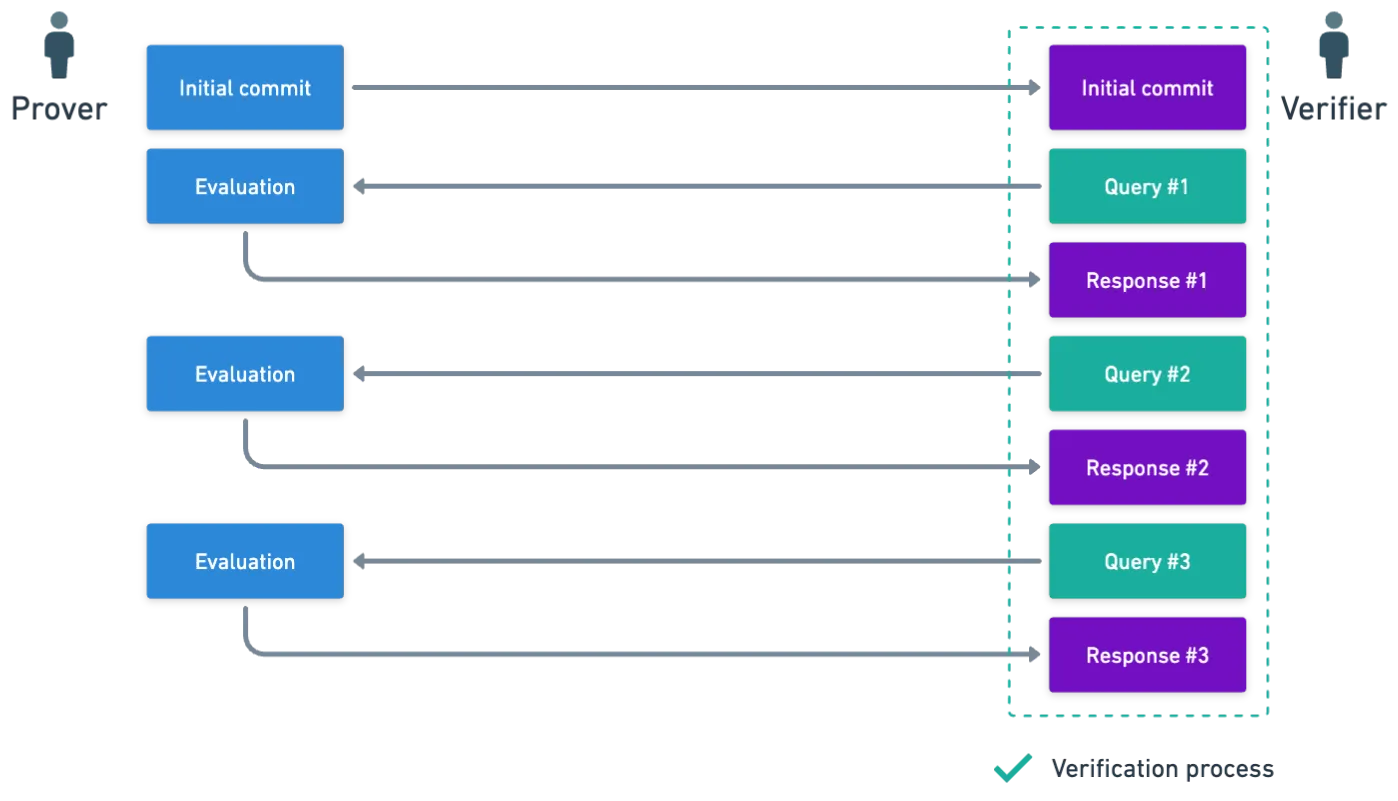
¡Espero que ya puedas ver cómo esta imagen se parece a la que usamos para describir los Esquemas de Compromiso Polinomial (PCSs)!
Y usaremos este modelo para realizar nuestras pruebas. Con fines ilustrativos, describamos cómo sería una prueba de cero.
Imagina que quieres probar que algún conjunto es una colección de raíces de un polinomio dado :
¿Qué puedes hacer al respecto? Bueno, dado que los valores en son raíces, puedes dividir el polinomio por lo que se llama un polinomio de anulación para el conjunto :
El término anulación se debe al hecho de que el polinomio es cero solo en el conjunto , por lo que son exactamente sus raíces.
Si realmente son las raíces de , entonces debería ser divisible por , sin resto.
Y ahora, vamos a tener que usar un Esquema de Compromiso Polinomial para continuar. ¡Puede que tengas que leer ese artículo primero!
Esencialmente, lo que sucede es que el probador se compromete tanto con como con , y luego, solicitan una evaluación en algún aleatorio. Con estas evaluaciones, pueden comprobar si lo siguiente es cierto:
Si resulta ser cero, entonces vimos que pueden concluir con alta probabilidad que este polinomio es exactamente cero! Lo que significa que:
Por lo tanto, pueden estar convencidos de que, efectivamente, es un conjunto de raíces de . Si por alguna razón no están convencidos, podrían pedir otro conjunto de evaluaciones de y , y ejecutar la verificación de nuevo.

Existen IOPs similares para la comprobación de suma y la comprobación de producto.
También vale la pena mencionar que esto no asegura que el polinomio no tenga otras raíces que no estén contenidas en . ¡Pero no iremos por ese camino esta vez!
De Interactivo a No-interactivo
Pero espera... ¿No dijimos que los SNARKs eran no interactivos? Entonces, ¿cómo es posible que algún protocolo interactivo sea una parte clave de nuestra construcción?
Resulta que hay una manera de convertir la interactividad en no interactividad: la transformación de Fiat-Shamir. Suena más intimidante de lo que es, confía en mí.
Si lo pensamos, podríamos preguntarnos "¿por qué estos protocolos son interactivos en primer lugar?" La razón es que en cada consulta, el verificador muestrea algún número aleatorio de algún conjunto. Y estos valores no pueden ser predichos por el probador — solo se vuelven disponibles para ellos cuando el verificador elige ejecutar una consulta. Esta impredecibilidad es una especie de mecanismo anti-trampa.
En lugar de esperar a que el verificador envíe valores aleatorios, podemos simular esta aleatoriedad usando una primitiva criptográfica bien conocida que también tiene una salida impredecible: funciones de hash!
No nos centremos en los detalles, sin embargo — todo lo que necesitas saber es que la heurística de Fiat-Shamir es una poderosa transformación, ¡que puede ser muy útil para convertir cualquier protocolo interactivo en uno no interactivo!
Después de lo que solo puede categorizarse como tortura, tenemos todos los elementos que necesitamos. Nuestro extenuante viaje está casi terminado — todo lo que queda es poner la cereza encima de esta pila de locuras.

De Vuelta a la Verificación
Bien, veamos. Recuerda, estamos tratando de convencer a un verificador de que conocemos tal que:
Y tenemos que convencerlos de algunas cosas:
- Entradas correctas
- Cálculo correcto de compuertas
- Cableado correcto
Comencemos con las entradas. El verificador tiene el testigo público, . Ahora, imagina que el verificador codifica este testigo en un polinomio , de modo que:
En este escenario, debería ser cierto que los valores y coinciden para las raíces de la unidad que codifican el testigo público:
Entonces, ¿qué hacemos? ¡Pues claro, una prueba de cero para el polinomio en las entradas que codifican el testigo!

¡Ajá! Comienza a tener sentido, ¿no es así?
Comprobando las Compuertas
De manera similar, recuerda que las compuertas deberían satisfacer la expresión:
Así que de nuevo, ¿qué haces? Una prueba de cero en esta expresión masiva, en cada compuerta. Maravilloso. Espléndido.
Para esto, por supuesto, el verificador necesitará un compromiso con .
Comprobando los Cables
Por último, necesitamos verificar las restricciones de cableado. Estas fueron codificadas en algunos polinomios que recorrían cíclicamente un conjunto de entradas , y teníamos que comprobar que:
Para cada elemento en . Esto no es realmente eficiente de hacer con pruebas de cero (aunque se puede hacer), así que hay una forma alternativa de hacerlo a través del uso de una comprobación de producto. Usando esta expresión casualmente mencionada:
Sí
La esencia de esto es que la expresión completa debería ser igual a ! Si lo piensas, tiene perfecto sentido: todos los valores deberían ser los mismos, y dado que permuta los elementos de , y porque el producto cubre todo , simplemente obtenemos:
Hay más que decir sobre esto, como ¿por qué necesitamos incorporar y en la mezcla? Pero honestamente, creo que es suficiente matemática por hoy.
En resumen, y para concluir: ¡usamos algunas IOPs para verificar las restricciones en un circuito aritmético, que fueron codificadas en polinomios!
Resumen
Uff. Eso fue un montón. Lo sé.

Aún así, me parece increíble cómo todas estas cosas se unen para formar un protocolo tan sofisticado: usamos interpolación polinómica para codificar cosas, esquemas de compromiso polinomial para consultar información, pruebas de oráculo interactivas para crear pruebas, y la heurística de Fiat-Shamir para convertir todo este lío en una prueba no interactiva. In-cre-í-ble.
El resultado final, Plonk, logra la generalidad que estábamos buscando al permitir que se use cualquier circuito. Y dado que esto no revela nada sobre , ¡entonces esto es realmente un SNARK de conocimiento cero (zkSNARK)!
Por razones de exhaustividad, diré que hay algunos otros detalles a considerar para asegurarse de que el protocolo sea de conocimiento cero, específicamente en torno a los desafíos. No te preocupes demasiado, sin embargo, ¡a menos que, por supuesto, estés planeando implementar Plonk tú mismo!
Para una mirada más interactiva, puedes consultar esta excelente lección en video.
¡Y aquí hay otro intento de explicar el protocolo, en caso de que te resulte más fácil de seguir!
Con suerte, ahora puedes entender mejor la breve descripción de Plonk que proporcioné al principio del artículo:
![]()
![]() En Plonk, codificamos el cálculo de un circuito en una serie de polinomios, que representan las restricciones impuestas por el circuito, para los cuales podemos probar afirmaciones mediante una serie de pruebas, sin revelar jamás los polinomios mismos — y por lo tanto, sin filtrar las entradas secretas.
En Plonk, codificamos el cálculo de un circuito en una serie de polinomios, que representan las restricciones impuestas por el circuito, para los cuales podemos probar afirmaciones mediante una serie de pruebas, sin revelar jamás los polinomios mismos — y por lo tanto, sin filtrar las entradas secretas.![]()
![]()
Dado que ahora podemos crear pruebas para circuitos arbitrarios, me gustaría volverme más práctico. Así que, la próxima vez, construiremos un par de circuitos para algunas afirmaciones, que luego pueden ser las entradas para Plonk, convirtiéndolas en zkSNARKS. ¡Hasta pronto!

¿Te resultó útil este contenido?
Apoya a Frank Mangone enviando un café. Todos los ingresos van directamente al autor.
