Criptografía 101: Pruebas de Conocimiento Cero (Parte 3)

Este artículo forma parte de una serie más larga sobre criptografía. Si este es el primer artículo con el que te encuentras, te recomiendo encarecidamente comenzar desde el principio de la serie.

¡Con la teoría detrás de nosotros, es hora de ser más prácticos!

En el artículo de hoy, me gustaría centrarme en algunos ejemplos simples de afirmaciones que podemos probar utilizando un zkSNARK como Plonk. Así que, esencialmente, estaremos construyendo algunos circuitos aritméticos.

Y no veo mejor manera de empezar esto que ¡revisitar las pruebas de rango! Vamos directo a la acción.

Pruebas de Rango Revisitadas

Durante nuestra no tan breve mirada a Bulletproofs, vimos lo difícil que era construir una prueba de rango desde cero. Pero ahora, tenemos algunas nuevas herramientas a nuestra disposición. Y como prometimos, veremos cómo podemos construir un circuito aritmético para representar la afirmación:

Hay una representación válida de N bits para un número $v$

¡Construir tal circuito nos permite probar el conocimiento de dicho número $v$ usando Plonk! Así que intentemos expresar esto en ecuaciones, de nuevo.

Realmente, este es el mismo sistema que describimos antes. Por lo tanto, la siguiente descripción será algo condensada — ¡recomiendo la explicación anterior para una mayor atención al detalle!

Si nuestro número $v$ puede ser representado con $N$ bits, esto significa que hay alguna representación binaria válida para él:

$$(b_0, b_1, b_2, b_3, ..., b_{N-1})$$

Y a su vez, estos números deberían satisfacer esta ecuación:

$$v = 2^0b_0 + 2^1b_1 + 2^2b_2 + ... + 2^{N-1}b_{N-1} = \sum_{i=0}^{N-1} 2^ib_i$$

También sabemos que todas nuestras entradas estarán en un campo finito de tamaño $q$:

$$x_i, w_j \in \mathbb{F}_q$$

Tanto $v$ como los $b_i$ serán entradas a nuestro circuito — por lo tanto, necesitamos alguna manera de probar que los valores $b_i$ son bits (ya sea $0$ o $1$). Y podemos hacer esto con la siguiente comprobación:

$$b_i(1 - b_i) = 0$$

Para cada uno de los N bits.

Resta

¡Genial! Ya tenemos el sistema... Pero ¿cómo lo convertimos en un circuito aritmético? En particular, necesitamos poder representar la resta, pero solo podemos usar compuertas de suma y multiplicación. ¿Qué hacer entonces?

Bueno, cuando trabajamos con campos finitos, existe el concepto de inversos aditivos! Piensa en restar $1$ como lo mismo que sumar $-1$. Pero, por supuesto, $-1$ no es un elemento de nuestro campo:

$$\mathbb{F}_q = \{0,1,2,3,..., q-1\}$$

¿Cómo nos ayuda esto, entonces? Verás, así como dijimos que la suma se envuelve hasta el principio del conjunto cuando el resultado es mayor que $q - 1$, también es cierto que la resta se envuelve hasta el final del conjunto cuando el resultado es menor que $0$.

Realmente, lo que sucede es que podemos mapear $-1$ al conjunto utilizando la operación módulo:

$$(-1) \ \textrm{mod} \ q = q - 1$$

También puedes ver esto expresado como $-1 \equiv q - 1 (\textrm{mod} \ q)$. Esto se llama una relación de congruencia, y se lee "$-1$ es congruente con $q - 1$ módulo $q$".

Hay mucho que decir sobre las relaciones de congruencia, que también definen clases de congruencia — pero evitaremos entrar en esos temas hoy. Puedes leer sobre ello aquí si estás interesado.

En conclusión, sumar $q - 1$ tiene exactamente el mismo efecto que restar $1$!

Esto funciona para cualquier grupo aditivo.

Juntándolo Todo

Ahora que sabemos cómo restar, ¡podemos crear nuestro circuito!

Para empezar, debemos verificar que $b_i$ es un bit. Esto se puede hacer de esta manera:

Click to zoom

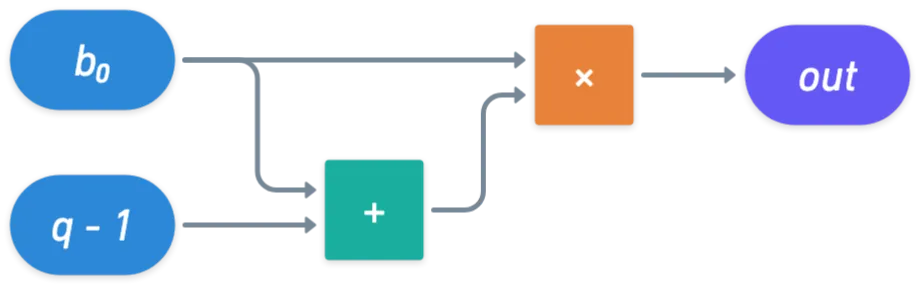
Por supuesto, si sumamos todas las salidas de estas verificaciones, el valor resultante también debería ser $0$.

Luego, necesitamos representar la suma de cada bit multiplicado por la potencia correspondiente de $2$. Una vez que obtengamos el resultado, restar $v$ también debería dar $0$. Y como podrías adivinar, restar $v$ es lo mismo que sumar $-v$, que por supuesto, es el resultado de multiplicar $-1$ y $v$.

Para mantener las cosas manejables, digamos que $N = 4$. Para esta cantidad de bits, nuestro circuito se vería así:

Click to zoom

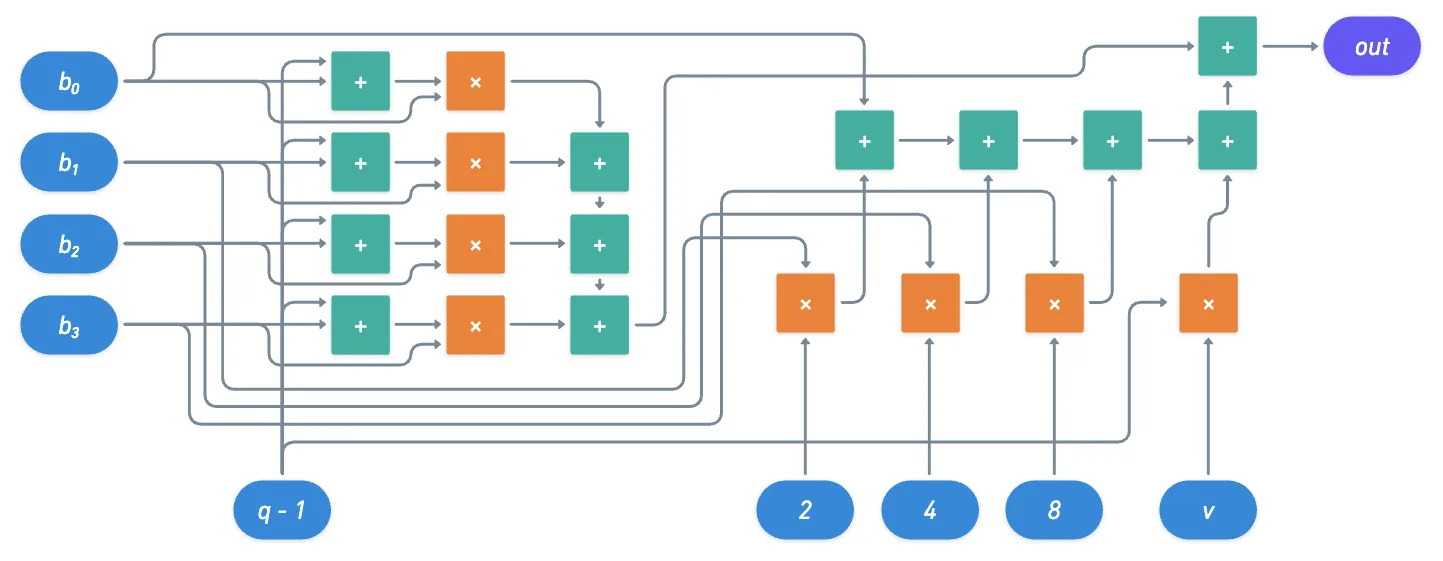
¡Y ahí lo tienes! Este circuito debería dar $0$ como salida si un número $v$ y su representación binaria $b_0$, $b_1$, $b_2$ y $b_3$ se introducen en él. Por supuesto, no queremos revelar ninguno de ellos — así que serán la afirmación privada. Todas las demás entradas pueden considerarse parte del testigo — solo un montón de valores que permiten una evaluación eficiente del circuito.

Si nos referimos a nuestra nomenclatura del artículo anterior, entonces la información secreta y el testigo serían:

$$x = (v, b_0, b_1, b_2, b_3) \in {\mathbb{F}_q}^5$$ $$w = (q - 1, 2, 4, 8) \in {\mathbb{F}_q}^4$$

A partir de aquí, todo lo que hacemos es aplicar Plonk como se presentó en el artículo anterior, ¡y entonces tenemos un zkSNARK para probar que $v$ está en el rango de $0$ a $15$. ¡Genial!

Pertenencia a Conjuntos

El ejemplo anterior introdujo un par de ideas interesantes, como cómo restar con compuertas. E implícitamente, también usamos algunos números mágicos como entradas, para evitar cálculos excesivos.

Sin embargo, estos no son los únicos trucos que podemos usar al construir circuitos — como veremos en un momento. Pasemos a nuestro siguiente ejemplo para ver qué nos espera.

Imagina que tenemos un conjunto de valores $S$:

$$S = \{s_0, s_1, s_2, ..., s_n\}$$

Lo que intentaremos hacer es probar el conocimiento de un valor $s_i$ que pertenece a dicho conjunto. Necesitaremos alguna afirmación matemática que represente este hecho. Esta es bastante fácil — aquí, simplemente escribiré la ecuación para ti:

$$P(x) = (x - s_0)(x - s_1)...(x - s_n) = \prod_{i=0}^n (x - s_i)$$

Si $s_i$ es, de hecho, parte del conjunto, entonces uno de los términos será cero, haciendo que todo el producto dé como resultado $0$. De lo contrario, el valor de $P(x)$ será algún valor positivo no cero.

Es decir, los $s_i$ son las raíces de $P(x)$.

Construir un circuito para este polinomio no es difícil. Probablemente implicaría proporcionar los valores $s_i$ como el testigo, para un cálculo más rápido, y para que el protocolo tenga algún sentido. Es decir, ¿de qué sirve probar el conocimiento de un valor en un conjunto, si el verificador no sabe de qué conjunto están hablando?

Sin embargo, parece haber un problema aquí: si $S$ es público, entonces todo el mundo puede leerlo. Así que en teoría, cualquiera podría probar el conocimiento de algún $s_i$ en el conjunto. Construir una prueba de conocimiento cero en ese escenario no tiene mucho sentido...

Ocultando el Conjunto

Arreglar esto no es difícil: para hacer el conjunto secreto, podemos hashear cada elemento, y hacer que los valores hasheados sean públicos en su lugar. El conjunto ahora se ve así:

$$S' = \{H(s_0), H(s_1), H(s_2), ..., H(s_n)\} = \{s'_0, s'_1, s'_2, ..., s'_n\}$$

Ahora estamos hablando

Con este ajuste, entonces conocer el conjunto $S'$ no revela nada sobre los valores reales en $S$, que permanecen secretos. Nuestra ecuación también necesita una ligera modificación:

$$P(x) = (H(x) - s'_0)(H(x) - s'_1)...(H(x) - s'_n) = \prod_{i=0}^n (H(x) - s'_i)$$

Por supuesto, la función de hash $H$ debe hashear en nuestro campo finito, para que podamos usar estos valores en nuestro circuito.

Maravilloso. Espléndido. Hasta que... Notamos que necesitamos incluir la función de hash en nuestro circuito.

Está bien, respira. No es tan malo. Por supuesto, si tuviéramos que implementar un circuito para una función de hash nosotros mismos, sería un verdadero dolor de cabeza.

Afortunadamente, algunas personas ya han pensado en esto, y proporcionan funciones de hash como paquetes en algunos Lenguajes de Dominio Específico (DSL) populares para construir circuitos, como Circom y Noir.

Por ejemplo, está Poseidon. Puedes encontrar su implementación aquí.

Pensemos en la función de hash como una caja, que incluiremos en nuestro circuito, como un componente. Con esto en mente, nuestro circuito se vería así:

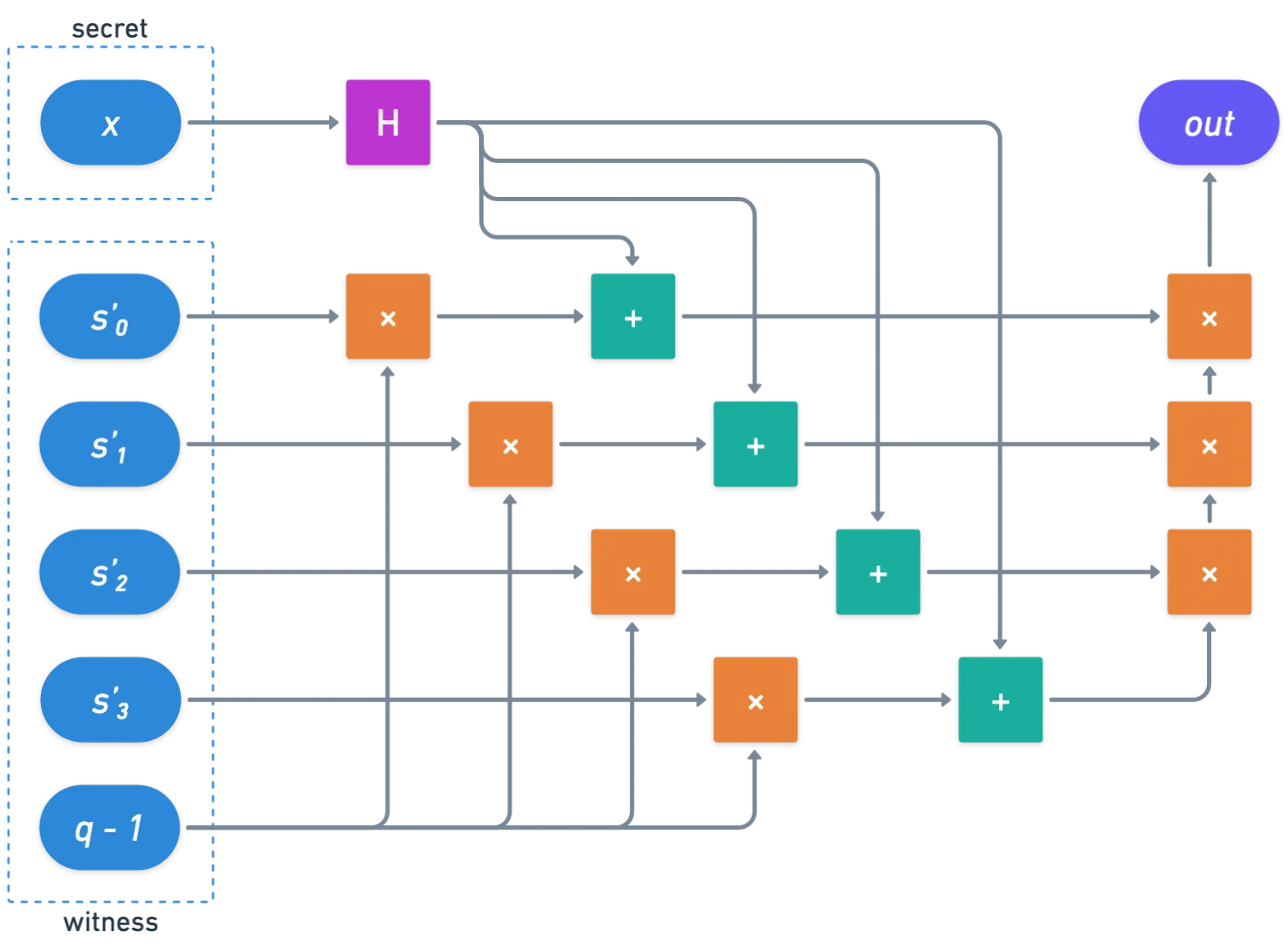
¡Impresionante! Todo lo que queda es ejecutar esto a través de Plonk — ya sabes, calculando el rastro, codificándolo, todas esas cosas buenas que ya discutimos en el capítulo anterior de la serie.

Verificación de Cero

Tener un componente de hash reutilizable para incluir en nuestros circuitos es ciertamente una buena idea. Uno puede preguntarse si hay otras acciones o verificaciones que podríamos querer reutilizar de manera similar — siendo así un buen objetivo para este tipo de proceso de caja negra.

¡Muy similar al proceso de crear componentes de computadora!

Una idea muy simple para tal componente, es construir algo que verifique si algún valor es cero o no. Es decir, una función que hace lo siguiente:

$$f(x) = \left\{\begin{matrix} 1 \ \textrm{si} \ x = 0 \\ 0 \ \textrm{si} \ x \neq 0 \end{matrix}\right.$$

Quiero decir, podría ser útil... ¿Quién sabe, verdad? ¡Verificar que algunos cálculos den $0$ en un circuito grande podría ser necesario! Además, no hay un if (x == 0) directo disponible para usar.

Construyamos tal componente. Aquí hay una idea para ello:

Click to zoom

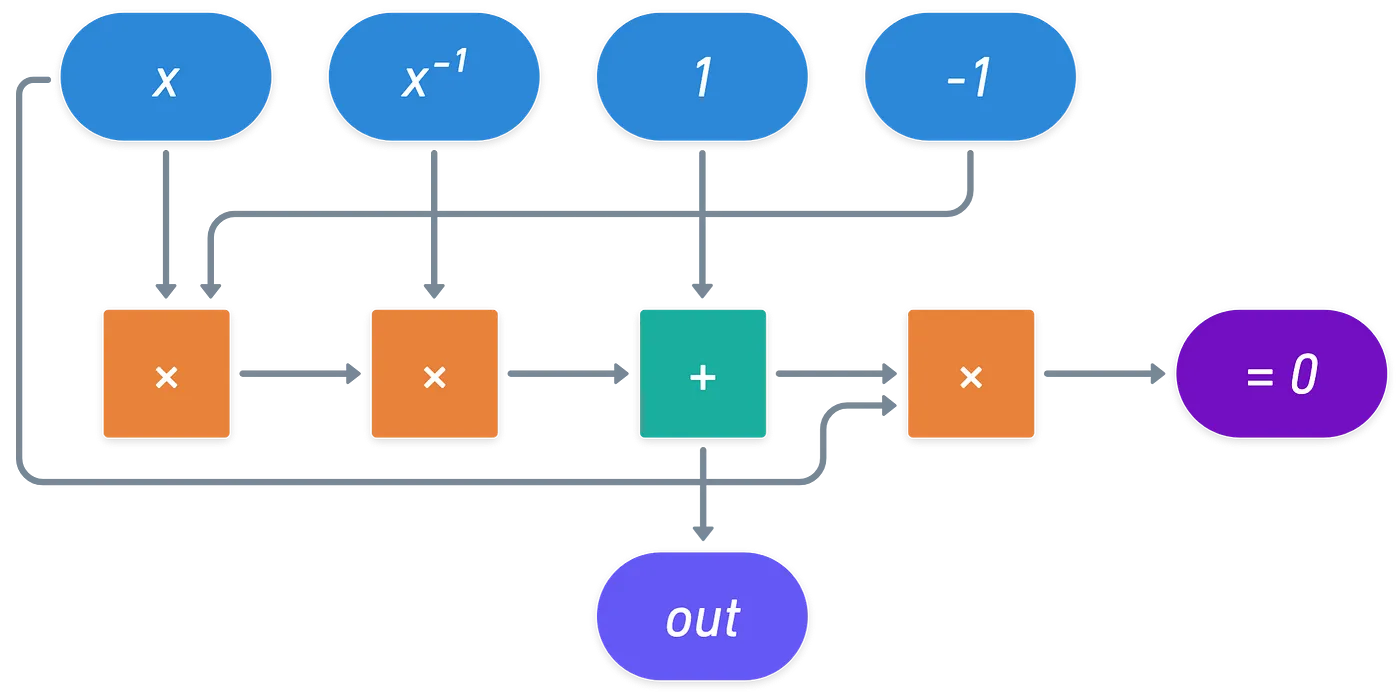
Una inspección más detallada paso a paso revela lo que está haciendo este circuito: las primeras tres compuertas calculan la expresión:

$$1 = x.x^{-1}$$

Si $x$ es $0$, entonces su inverso también será cero, y la expresión dará $1$. Si $x$ no es $0$, entonces por definición sabemos que $x.x^{-1} = 1$, y por lo tanto, la expresión devolverá $0$.

Esta es la razón por la que la salida de este componente no está en la última compuerta, sino en la tercera. Entonces, ¿por qué hay una cuarta compuerta? ¿Qué propósito tiene?

Para responder a la pregunta, te preguntaré: ¿no has notado algo fuera de lo común en este circuito? Míralo de nuevo.

Pronto te darás cuenta de que esta es la primera vez que usamos un inverso modular. Es una entrada a nuestro circuito — simplemente no podemos calcular inversos modulares solo con compuertas de suma y multiplicación. Y así, el valor del inverso modular debe ser proporcionado.

Recuerda que en Plonk, solo verificamos que el rastro de cálculo tenga sentido — está perfectamente bien que se proporcione un inverso como entrada, ¡siempre que nos aseguremos de que el valor sea correcto!

La idea es que la cuarta compuerta existe como un medio para verificar que el inverso modular reclamado es de hecho correcto. Llamemos al inverso modular reclamado $y$. En total, hay cuatro escenarios posibles para analizar, que puedes corroborar tú mismo siguiendo el circuito:

• $x = 0$: No importa qué inverso proporcionemos, la salida será $1$. Realmente no nos importa si el inverso está bien o no, lo cual es consistente con que la última compuerta siempre dé $0$.
• $x \neq 0, y = x^{-1} \neq 0$: El inverso es correcto, y la salida es $0$. La última compuerta también debería dar $0$, lo que significa que el inverso es correcto.
• $x \neq 0, x^{-1} = 0$: El inverso es incorrecto. La salida será $1$ (que es incorrecta), y además, la última compuerta no dará $0$. ¡Debido a que la última restricción no se cumple, esto significa que algo en las entradas está mal!
• $x \neq 0, y \neq x^{-1} \neq 0$: El inverso es incorrecto, y en este caso, la salida no será $1$, sino algún otro elemento en el campo finito. Debido a esto, la última compuerta ciertamente no dará $0$ — y esto significa que el inverso proporcionado no es correcto.

¡Y ahí lo tienes! Nuestro circuito verificador de cero está listo.

Tener estos elementos simples que realizan tareas simples puede ser enormemente útil a medida que construimos circuitos cada vez más grandes. Permite cierto grado de componibilidad en el proceso, ¡lo que puede acelerar dramáticamente la creación de tus circuitos!

Resumen

Estos son solo algunos ejemplos de las cosas que puedes hacer con circuitos aritméticos: dado que son un modelo de cálculo tan general, puedes construir casi cualquier tipo de afirmación.

Es cierto que crear el circuito en sí mismo podría ser un poco desafiante si tuviéramos que unir muchas compuertas nosotros mismos. Por eso nunca lo hacemos realmente.

Usamos otros tipos de representaciones, que pueden ser conceptualizadas como circuitos.

Circom, que es un DSL popular para construir circuitos, no te obliga a escribir compuertas. En su lugar, se basa en una técnica llamada aritmetización para transformar un conjunto de restricciones en la forma adecuada para zkSNARKs.

Finalmente, los SNARKs tienen muchos beneficios (tamaños de prueba pequeños, tiempos de verificación cortos), pero también hay algunos aspectos que generan cierto grado de preocupación (por ejemplo, Plonk requiere una configuración de confianza). Por esta razón (y otras), esta sigue siendo un área de investigación muy activa. ¡Quién sabe qué podríamos ver en el futuro!

Hablando de configuraciones de confianza e idealmente evitándolas, hay otro tipo de prueba sucinta de conocimiento que no lo requiere — es transparente. Así que en el próximo capítulo de nuestra aventura, exploraremos el mundo de los STARKs, el hermano menor de los SNARKs que trae algunas propiedades interesantes a la mesa. ¡Hasta la próxima!