Criptografía 101: Pruebas de Conocimiento Cero (Parte 1)

Este artículo forma parte de una serie más larga sobre criptografía. Si este es el primer artículo con el que te encuentras, te recomiendo encarecidamente comenzar desde el principio de la serie.

¡Finalmente es hora de algunas pruebas de conocimiento cero!

Anteriormente en esta serie, esbozamos qué son. Sin embargo, esta vez seremos más minuciosos en nuestra definición y veremos un ejemplo más avanzado.

La idea general de una ZKP es convencer a alguien sobre la verdad de una afirmación respecto a cierta información, sin revelar dicha información. Dicha afirmación podría ser de diferentes naturalezas. Podríamos querer probar:

• conocimiento de un logaritmo discreto (el protocolo de Schnorr)
• que un número está en un cierto rango
• que un elemento es miembro de un conjunto

entre otros. Normalmente, cada una de estas afirmaciones requiere un sistema de prueba diferente, lo que significa que se requieren protocolos específicos. Esto es algo poco práctico — y sería realmente bueno si pudiéramos generalizar las pruebas de conocimiento.

Así que nuestro plan será el siguiente: veremos una técnica de ZKP llamada Bulletproofs. Veremos cómo resuelven un problema muy específico, y en los próximos artículos, evaluaremos cómo casi lo mismo se puede lograr de una manera más general.

Nos centraremos solo en la versión simple, no optimizada (¡ya es bastante complicada!). Y si este artículo no es suficiente para saciar tu curiosidad, quizás el artículo original o este artículo sean lo que estás buscando.

Comencemos con una introducción suave al tema, antes de sumergirnos en las matemáticas.

Fundamentos de Conocimiento Cero

Cuando hablamos de probar la validez de afirmaciones, la familia más amplia de técnicas se llama pruebas de conocimiento. En estos tipos de protocolos, generalmente hay dos actores involucrados: un probador y un verificador.

Y también hay dos elementos clave: una afirmación que queremos probar, y un testigo, que es una pieza de información que permite verificar eficientemente que la afirmación es verdadera. Algo como esto:

Click to zoom

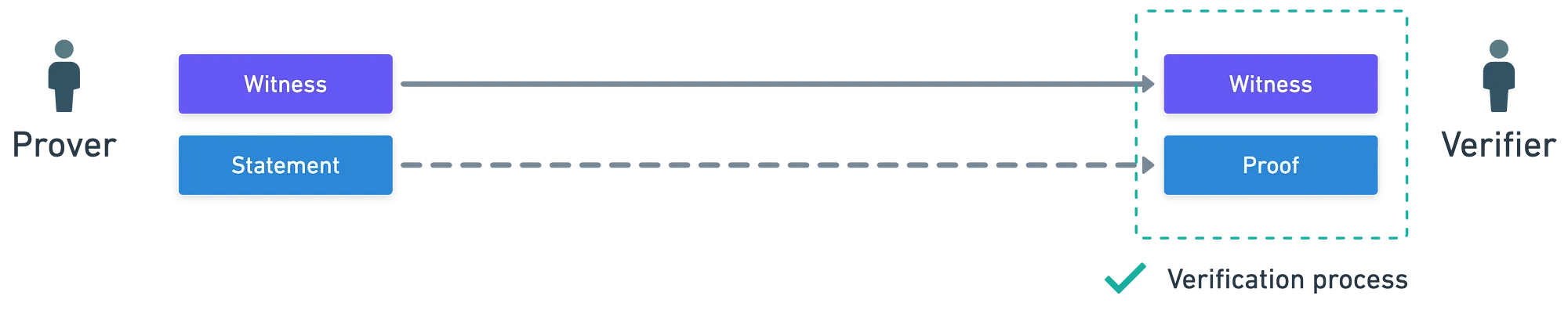
¡Solo que esta no es toda la historia!

Si recuerdas nuestra breve mirada al protocolo de Schnorr, vimos cómo había cierta comunicación de ida y vuelta entre el probador y el verificador. Y hay una buena razón para esto: el verificador proporciona una pieza de información impredecible al probador. Lo que esto logra es hacer extremadamente difícil producir pruebas falsas — y muy simple producir pruebas válidas, siempre y cuando el probador sea honesto. Este factor "comodín" se denomina típicamente un desafío.

Un Ejemplo Simple

Para entender mejor esta idea, aquí hay un ejercicio muy simple: imagina que Alicia coloca una secuencia secreta de cartas de póker boca abajo sobre una mesa. Bruno, que está sentado al otro lado de la mesa, quiere verificar que Alicia conoce dicha secuencia secreta. ¿Qué puede hacer al respecto?

Bueno, podría preguntar "dime qué carta está en la cuarta posición". Si Alicia realmente conoce la secuencia, puede responder con confianza "7 de espadas", y Bruno podría simplemente mirar la carta boca abajo y verificar que coincide. Bruno ha proporcionado un desafío al seleccionar una carta, y es solo a través del conocimiento honesto de la secuencia que Alicia puede proporcionar información correcta. De lo contrario, tendría que adivinar — y es improbable que diga la carta correcta.

Concedido, esto no es conocimiento cero, ¡porque se revelan partes de la secuencia!

Agregando este desafío a la mezcla, obtenemos una imagen más completa:

Click to zoom

La idea es que el probador hace un compromiso con su información, antes de conocer la entrada del verificador (en nuestro ejemplo, Alicia se compromete colocando las cartas boca abajo) — y esto de alguna manera les impide hacer trampa.

Formalmente, la estructura que acabamos de describir es típica de los protocolos Sigma. También puedes ver el término verificador de Moneda Pública, que simplemente significa que la elección aleatoria del verificador se hace pública. Ya sabes, ¡solo para evitar confusiones!

Para finalizar nuestra breve introducción, aquí están las dos propiedades clave que las pruebas de conocimiento deberían satisfacer:

• Completitud: Un probador honesto con una afirmación honesta puede convencer a un verificador sobre la validez de la afirmación.
• Solidez: Un probador con una afirmación falsa no debería poder convencer a un verificador de que la afirmación es verdadera. O realmente, debería haber una probabilidad muy baja de que esto suceda.

Ahora, si agregamos la condición de que la prueba no revele nada sobre la afirmación, entonces tenemos una prueba de conocimiento cero. No entraremos en definir formalmente qué significa "no revelar nada", pero hay algunos recursos que explican la idea si quieres profundizar más.

Con esto, la introducción ha terminado. Turbulencia por delante, agárrate fuerte.

Pruebas de Rango

Como mencionamos anteriormente, un elemento crucial que necesitamos decidir es qué queremos probar. Por ejemplo, en el caso del protocolo de Schnorr, queremos probar el conocimiento del logaritmo discreto de un valor.

Otra afirmación que podríamos desear probar es que algún valor se encuentra dentro de un rango. Esto puede ser útil en sistemas con saldos privados, donde es importante probar que después de realizar una transacción, el saldo restante es no negativo (positivo o cero). En ese caso, solo necesitamos probar que dicho valor se encuentra en un rango:

$$b \in [0, 2^{n-1} - 1]$$

Y aquí es donde entran en juego técnicas como Bulletproofs. Ahora... ¿Cómo demonios vamos a probar esto?

Cambiando Perspectivas

Piensa en un número $v$ representado por un byte (8 bits). Entonces, este número solo puede estar en el rango de $0$ a $255$ ($2^8 - 1$). Así que, si podemos probar la afirmación:

Hay una representación válida de 8 bits de $v$

Entonces hemos construido una prueba de conocimiento de que $v$ se encuentra entre $0$ y $255$. Y eso es todo lo que haremos, en esencia.

Click to zoom

Sin embargo, debemos convertir esta idea en un conjunto de restricciones matemáticas que representen nuestra afirmación.

Para empezar, denotemos los bits de $v$ por los valores $a_{l,0}$, $a_{l,1}$, $a_{l,2}$, y así sucesivamente — siendo $a_{l,0}$ el bit menos significativo. Esto significa que se cumple la siguiente igualdad:

$$a_{l,0}2^0 + a_{l,1}2^1 + a_{l,2}2^2 + ... a_{l,n-1}2^{n-1} = v$$

Para evitar expresiones largas y engorrosas, introduzcamos una nueva notación. Piensa en nuestro número $v$ representado como un vector binario, cada componente siendo un bit:

$$\vec{a_l} = (a_{l,0}, a_{l,1}, a_{l,2}, ..., a_{l,n-1}) \in {\mathbb{Z}_q}^n$$

Y también, definamos esto:

$$\vec{W}^n = (W^0, W^1, W^2, ..., W^{n-1}) \in {\mathbb{Z}_q}^n$$

Podemos introducir cualquier valor para $W$ — y en particular, introducir $0$ o $1$ resulta en un vector de ceros o unos, respectivamente.

Ahora, podemos ver que la ecuación anterior se puede escribir como un producto interno:

$$\langle \vec{a_l}, \vec{2}^n \rangle = a_{l,0}2^0 + a_{l,1}2^1 + a_{l,2}2^2 + ... a_{l,n-1}2^{n-1} = v$$

Ah, los recuerdos del álgebra lineal

Esta notación es bastante compacta, así que utilizaremos expresiones similares a lo largo de este artículo.

Si esta ecuación se cumple, significa que $a_l$ representa correctamente a $v$, y en consecuencia, que $v$ está en el rango esperado. Excepto que, de nuevo, esa no es toda la historia.

Nos falta un pequeño detalle: ¡los valores en $a_l$ podrían no ser ceros y unos! Los posibles valores para cada dígito o componente del vector pueden realmente variar de $0$ a $q$, dependiendo de qué campo finito estemos usando. En otras palabras: cada componente puede ser cualquier elemento en los enteros módulo $q$. Y la igualdad todavía podría cumplirse.

Así que requeriremos una condición adicional. Para esto, definimos:

$$\vec{a_r} = \vec{a_l} - \vec{1}^n$$

Todo lo que estamos haciendo ahí es restar $1$ de cada elemento de nuestro vector. Lo que significa que:

• Si algún componente $a_{l,i}$ tiene valor $1$, entonces $a_{r,i}$ tendrá valor $0$
• Si $a_{l,i}$ tiene valor $0$, entonces $a_{r,i}$ dará la vuelta (una especie de underflow, si quieres) a $q - 1$.
• De lo contrario, ni $a_{l,i}$ ni $a_{r,i}$ tendrán valor $0$.

Esto es importante porque si $a_l$ realmente es un número binario, debería suceder algo como esto:

Click to zoom

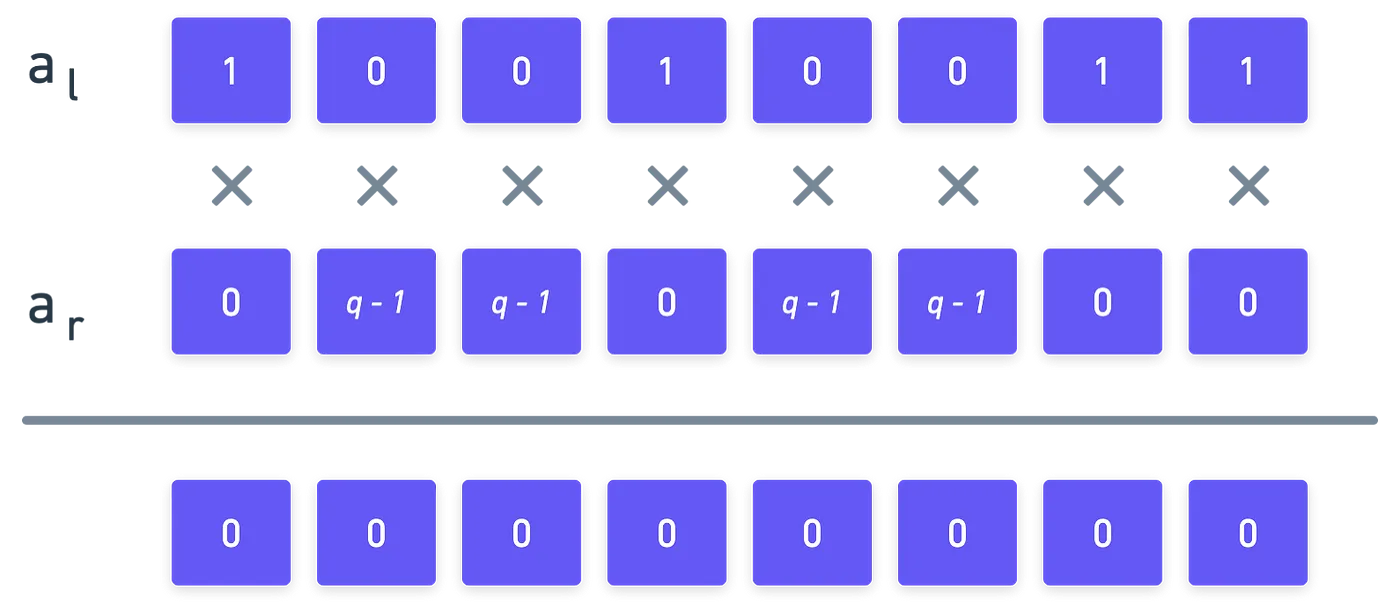
¡Mira eso! Siempre que nuestra representación binaria sea correcta, entonces el producto interno de $a_l$ y $a_r$ dará como resultado $0$!

$$\langle \vec{a_l}, \vec{a_r} \rangle = 0$$

Resumiendo, tenemos un total de dos condiciones que conforman nuestra afirmación (recuerda, la afirmación es lo que queremos probar).

$$\left \{ \begin{matrix} \langle \vec{a_l}, \vec{2}^n \rangle = v \\ \\ \langle \vec{a_l}, \vec{a_r} \rangle = 0 \end{matrix}\right.$$

El Protocolo

Nuestro sistema está configurado. Si conocemos los valores de $v$ y $a_l$, entonces verificar que la representación binaria es correcta es bastante sencillo — simplemente comprobamos que el sistema se cumple.

Sin embargo, dado que estamos siguiendo la ruta de conocimiento cero, el verificador no conocerá estos valores. Así que para convencerlo, el probador tendrá que hacer algo de magia — nada sorprendente, a estas alturas de la serie.

Los Compromisos

Todo comienza con compromisos. Recuerda que los compromisos solo pueden abrirse con valores válidos — por lo tanto, vinculan al probador con la afirmación que quiere probar.

Comencemos comprometiéndonos con el valor $v$. Para esto, se utiliza un compromiso de Pedersen. Usaremos un grupo multiplicativo $\mathbb{G}$ de orden primo $q$ (consulta el artículo sobre isomorfismos si necesitas un repaso, o revisa el artículo anterior), con generadores $g$, $h$.

El compromiso se ve así:

$$V = g^vh^{\gamma}$$

En segundo lugar, queremos comprometernos con $a_l$ y $a_r$, que también son parte de nuestro sistema. Como estos son vectores, necesitaremos un compromiso ligeramente más complejo. Usaremos generadores $g_k$ y $h_k$, con $k$ que va de $0$ a $n$. Aquí, la cantidad de bits en nuestro rango será $n + 1$. Y aquí está el compromiso (redoble de tambores por favor):

$$A = h^{\alpha}\prod_{i=0}^n {g_i}^{a_{l,i}}{h_i}^{a_{r,i}} = h^{\alpha}{\vec{g}}^{\vec{a_l}}{\vec{h}}^{\vec{a_r}}$$

Vaya, vaya, hay muchos símbolos ahí! Detengámonos y examinemos la expresión.

El símbolo grande $\Pi$ es un producto, que es como una sumatoria, pero en lugar de sumar términos, los multiplicamos.

Para hacer la expresión menos intimidante, usamos notación vectorial. Con ella, nos ahorramos el tiempo de escribir el símbolo del producto, pero en realidad, ambas expresiones representan lo mismo.

Lo interesante de los compromisos de Pedersen es que podemos combinar muchos valores en un solo compromiso, con solo un factor de cegado. ¡Estupendo!

También necesitaremos factores de cegado para los componentes de $a_l$ y $a_r$ — estos serán dos vectores muestreados aleatoriamente $s_l$ y $s_r$, a los que nos comprometemos con:

$$S = h^{\rho}\prod_{i=0}^n {g_i}^{s_{l,i}}{h_i}^{s_{r,i}} = h^{\rho}{\vec{g}}^{\vec{s_l}}{\vec{h}}^{\vec{s_r}}$$

Estos compromisos se envían al verificador, de modo que el probador está vinculado a v y a su representación binaria.

El Desafío

Ahora que el verificador tiene algunos compromisos, puede proceder a hacer un desafío. Para esto, elegirá dos números aleatorios $y$ y $z$, y los enviará al probador.

Lo que hace el probador ahora es bastante enrevesado y confuso, para ser honesto. Y esto es parte del punto que quiero señalar en este artículo: tal vez intentar elaborar un marco más general para las pruebas de conocimiento cero podría ser una idea interesante.

El probador calculará tres expresiones, que realmente representan un montón de polinomios (2n + 1 en total, para ser precisos). Intentaremos entenderlo en un momento — por ahora, simplemente sigamos con las definiciones. Estos polinomios son:

$$l(X) = (\vec{a_l} - z \cdot \vec{1}^n) + \vec{s_l} \cdot X \in {\mathbb{Z}_q}^n$$ $$r(X) = \vec{y}^n \circ (\vec{a_r} + z \cdot \vec{1}^n + \vec{s_r}) + z^2 \cdot \vec{2}^n \in {\mathbb{Z}_q}^n$$ $$t(X) = \langle l(X), r(X) \rangle = t_0 + t_1X + t_2X^2 \in {\mathbb{Z}_q}$$

Sé que así es como me sentí la primera vez que vi esto:

Hay mucho que desempacar aquí. Primero, un par de aclaraciones sobre la notación:

• El producto punto ($\circ$) se interpretará como multiplicación componente por componente. Esto es, si escribimos $a \circ b$, entonces el resultado será un vector de la forma $(a_0b_0, a_1b_1, a_2b_2, ...)$. Esto se usa en la expresión $r(X)$.
• El producto escalar ($\cdot$) se usa para multiplicar cada componente de un vector por un escalar (un entero, en nuestro caso). Así que por ejemplo, $z \cdot a$ (donde $z$ es un escalar) dará como resultado un vector de la forma $(za_0, za_1, za_2, ...)$.

En particular, concentrémonos en el término independiente del último polinomio, $t_0$. Se puede calcular mediante esta expresión:

$$t_0 = z^2.v + \delta(y,z)$$ $$\delta(y,z) = (z - z^2).\langle \vec{1}^n, \vec{y}^n \rangle - z^3.\langle \vec{1}^n, \vec{2}^n \rangle$$

Observa que $\delta$ es una cantidad que el verificador puede calcular fácilmente, lo que será útil en un minuto.

Importante, este término contiene el valor $v$, que es central para nuestra afirmación original. De alguna manera, probar el conocimiento de un $t_0$ "correcto" está ligado a probar el conocimiento de $v$. Y esto es exactamente lo que viene a continuación: proporcionar una evaluación correcta de los polinomios.

Así, el verificador se compromete con los coeficientes restantes de $t(X)$, $t_1$ y $t_2$ — muestreando algunos factores de cegado aleatorios $\tau_1$ y $\tau_2$, y calculando:

$$T_1 = g^{\tau_1}h^{t_1} \in \mathbb{G}$$ $$T_2 = g^{\tau_2}h^{t_2} \in \mathbb{G}$$

Y estos se envían al verificador. Pero aún no hemos terminado...

El Segundo Desafío

Para que esto funcione, requeriremos otro desafío más. Si lo piensas, esto tiene sentido debido a cómo hemos enmarcado el protocolo hasta ahora: tenemos un montón de polinomios, así que ahora necesitamos evaluarlos.

Y así, el verificador muestrea un nuevo desafío $x$, y lo envía al probador. Con él, el probador procede a calcular:

$$\vec{l} = l(x), \ \vec{r} = r(x), \ \hat{t} = \langle \vec{l}, \vec{r} \rangle$$

Se requieren dos herramientas más para que la prueba funcione. El probador necesita calcular:

$$\mu = \alpha + \rho x$$ $$\tau_x = \tau_2 x^2 + \tau_1 x + z^2 \gamma$$

No te preocupes demasiado por estos — solo son necesarios para que las matemáticas funcionen. De hecho, actúan como factores de cegado compuestos.

Finalmente, todos estos valores (los vectores $\vec{l}$ y $\vec{r}$, $\hat{t}$ y los factores de cegado) se envían al verificador, quien por fin procede al paso de verificación. ¡Hurra!

Verificación

En este punto, el verificador ha recibido varios valores del probador, concretamente:

$$V, A, S, T_1, T_2, \mu, \tau_x, \vec{l}, \vec{r}, \hat{t}$$

Como se mencionó anteriormente, lo que el verificador quiere comprobar es que las evaluaciones polinomiales son correctas. Y a su vez, esto debería convencer al verificador de que $v$ está en el rango especificado. La conexión entre estas dos afirmaciones no es evidente, sin embargo — así que intentaré dar algo de contexto a medida que avanzamos.

Vinculando los Polinomios

La primera igualdad que el verificador comprueba es esta:

$$g^{\hat{t}}h^{\tau_x} \stackrel{?}{=} V^{z^2}g^{\delta(y,z)}{T_1}^x{T_2}^{x^2}$$

Si estás interesado, esto tiene sentido porque:

$$V^{z^2}g^{\delta(y,z)}{T_1}^x{T_2}^{x^2} = (h^{\gamma}g^v)^{z^2}g^{\delta(y,z)}(g^{t_1}h^{\tau_1})^x(g^{t_2}h^{\tau_2})^{x^2}$$ $$g^{vz^2 + t_1x + t_2x^2 + \delta(y,z)}h^{\tau_2x^2 + \tau_1x + z^2 \gamma} = g^{\hat{t}}h^{\tau_x}$$

¿Qué significa todo esto? Si prestas mucha atención, verás que en un lado de la igualdad tenemos la evaluación $t(X)$, y en el otro lado, el valor $v$ (presente en el compromiso $V$). Así que lo que esta igualdad comprueba efectivamente es que el valor $t(x)$ está vinculado al valor original $v$. Entonces, el conocimiento de $t(x)$ también significa conocimiento de $v$. ¡Esto es de lo que el verificador debería estar convencido por esta igualdad! En resumen:

Esta comprobación convence al verificador de que $v$ es correcto siempre y cuando $t(x)$ también sea correcto

Para la siguiente comprobación, necesitaremos definir este nuevo vector:

$$h'_i = h_i^{y^{-i+1}} \rightarrow \vec{h'} = (h_1, h_2^{y^-1}, h_3^{y^-2}, ...)$$

Por muy enrevesado que pueda parecer esto, en realidad hace que la próxima comprobación funcione de maravilla. El verificador primero calcula:

$$P = AS^x(\vec{g})^{-z}(\vec{h'})^{z\vec{y}^n + z^2\vec{2}^n} \in \mathbb{G}$$

Y luego evalúa:

$$P \stackrel{?}{=} h^{\mu}(\vec{g})^{\vec{l}}(\vec{h'})^{\vec{r}}$$

Esta vez no proporcionaré una prueba de que las expresiones deberían coincidir — creo que es un buen ejercicio en caso de que estés interesado y no quieras tomar mi palabra!

Ya sea que elijas creerme o comprobarlo por ti mismo, esto es lo que está sucediendo aquí: $P$ contiene los valores para todos los valores $a_l$ y $a_r$, mientras que en el otro lado de la igualdad, tenemos las evaluaciones de $l(X)$ y $r(X)$. Debido a que el probador recibió un desafío del verificador ($x$), es inviable que $P$ satisfaga la igualdad si los polinomios están evaluados incorrectamente. En definitiva, esto es lo que sucede:

Esta comprobación convence al verificador de que la representación en bits de $v$ (los vectores $a$) es correcta siempre y cuando $l(x)$ y $r(x)$ sean correctos

Así que, finalmente, necesitamos comprobar que las evaluaciones de los polinomios coinciden. Y esto es muy fácil de comprobar:

$$\hat{t} \stackrel{?}{=} \langle \vec{l}, \vec{r} \rangle$$

Esta comprobación asegura que $\hat{t}(x)$ coincide con el valor esperado. Si bien es simple elegir valores de $t(x)$, $l(x)$ y $r(x)$ que se ajusten a esta expresión, es extremadamente improbable que también satisfagan las dos comprobaciones anteriores. Así que, en conjunto con ellas, lo que hace es:

Esta comprobación convence al verificador de que las evaluaciones polinomiales son correctas

¡Et voilà! Esa es la prueba completa. Un pedazo de torta, ¿verdad?

Diré esto de nuevo, ya que la reafirmación en esta etapa podría ser importante: esto es muy entreverado y ciertamente no es simple. Pero hey, ¡funciona!

Resumen

Sé que esta no fue una lectura ligera — probablemente todo lo contrario. Sin embargo, no hay muchas formas de esquivar la complejidad del protocolo, ¡es lo que es! Pero al final, somos capaces de cumplir nuestro propósito, y tenemos una forma de probar que un número se encuentra en un rango dado.

Alejándonos un poco, lo que podemos ver es que nuestra afirmación era bastante simple de plantear. Tres ecuaciones simples, y listo. Aún así, necesitamos una elaborada gimnasia criptográfica para demostrarlo.

Y esto está completamente bien, pero también despierta cierta inquietud: ¿podemos ser más generales? ¿Existe un marco más general para probar afirmaciones?

De hecho, lo hay. No me malinterpretes — los Bulletproofs y otros tipos de ZKP hechos a medida son muy interesantes, útiles y quizás más eficientes que una implementación generalizada. Pero si cada afirmación requiere investigación específica e implementaciones complejas, entonces puede convertirse en un cuello de botella para nuevas aplicaciones.

Es con este espíritu que avanzaremos en la serie — explorando un cierto marco para pruebas más generales: SNARKs. Pero primero necesitaremos sentar algunas bases — ¡y ese será el tema del próximo artículo!