Criptografía 101: Esquemas de Compromiso Revisitados

Este artículo forma parte de una serie más larga sobre criptografía. Si este es el primer artículo con el que te encuentras, te recomiendo encarecidamente comenzar desde el principio de la serie.

¡Muy bien! A estas alturas, ya hemos visto los emparejamientos en acción, en el contexto de la criptografía basada en identidad. Pero también hemos visto que los emparejamientos son poderosos por sí mismos, permitiendo otros métodos que no dependen de la identidad. En este artículo, me gustaría expandir esa idea.

Es hora de revisar un concepto de algunos artículos atrás: los esquemas de compromiso. Anteriormente definimos qué son: formas de comprometerse con un valor, sin revelarlo con antelación.

Una especie de mecanismo criptográfico anti-trampas.

Esta vez, examinaremos un tipo de esquema de compromiso que aún no hemos mencionado: los compromisos polinomiales. En particular, el método que se presentará es el que se describe en este artículo: el compromiso KZG (Kate-Zaverucha-Goldberg).

Una Breve Aclaración

Creo que, a esta altura de la serie, sería difícil etiquetar los artículos como 101 — en el sentido de que ya no son tan introductorios. Independientemente, el espíritu de estas presentaciones es hacer que el contenido y la notación algo crípticos de los artículos académicos sean un poco más accesibles. En este sentido, es cierto que he eliminado algunos elementos complejos, pero aun así, esto no significa que estos temas sean más fáciles.

Sin embargo, si has llegado a este punto de la serie, probablemente significa que estás muy interesado en comprender conceptos criptográficos complejos. Así que felicitaciones por el esfuerzo, gracias por seguir leyendo, ¡y espero que aún encuentres útil el contenido!

Comprometiéndose con un Polinomio

Nuestra descripción de los esquemas de compromiso hasta ahora solo cubre realmente el escenario donde hay un valor secreto que no queremos revelar con antelación. Y abrir el compromiso significa revelar el valor.

Pero, ¿y si pudiéramos tener toda una fábrica de compromisos?

Es decir, ¿qué pasaría si pudiéramos comprometernos con una función? Entonces, lo que podríamos hacer es proporcionar evaluaciones de la función a un verificador, y ellos pueden comprobar su evaluación correcta usando nuestro compromiso.

Para ser justos, aunque esto suena como una idea interesante para seguir, no está inmediatamente claro si hay aplicaciones adecuadas.

Así que para mantenerlos motivados, diré esto: comprometerse con una función es un ingrediente clave en algunas Pruebas de Conocimiento Cero que veremos en artículos futuros.

Además, recuerda que cuando hablamos de criptografía de umbral, mencionamos que había situaciones que requerían compartición de secretos verificable. Esto es, no solo se requieren las evaluaciones de un cierto polinomio, sino también una prueba de su corrección.

Los esquemas de compromiso polinomial pueden ayudar en este sentido.

El contexto está (más o menos) establecido. Quizás un diagrama ayude a aclarar lo que quise decir antes:

Click to zoom

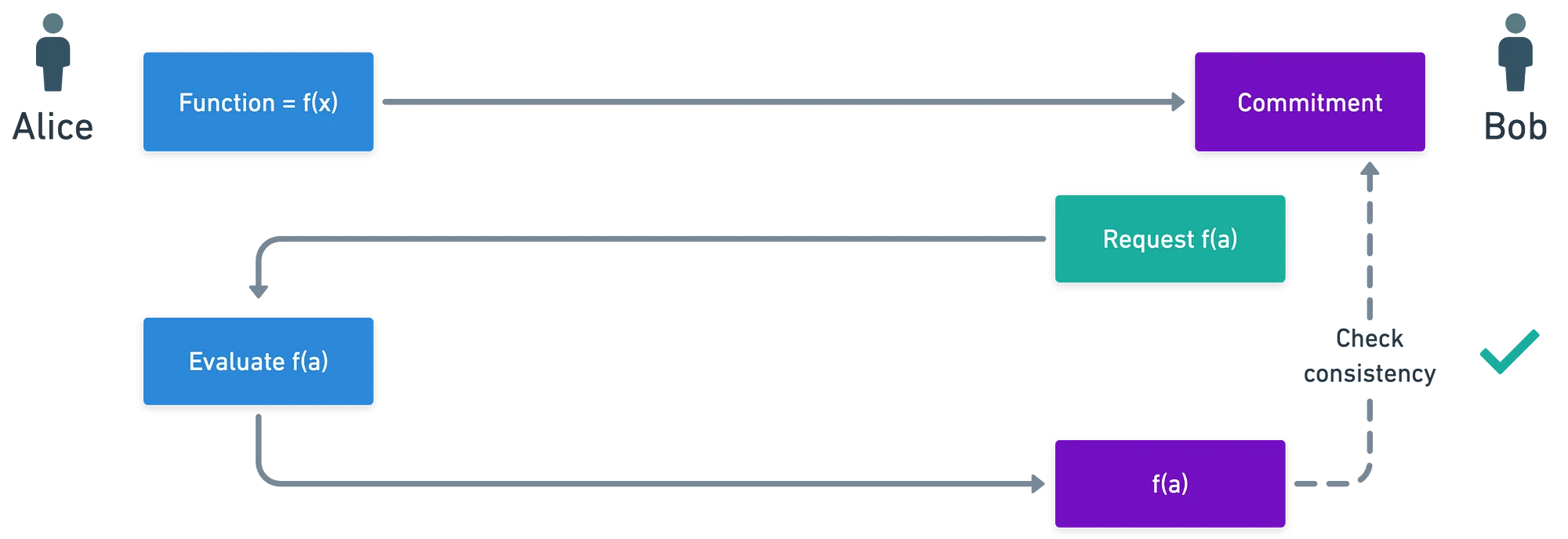
Observa que en el diagrama anterior, la función $f$ es secreta y nunca se revela realmente. Y como ya estarás adivinando a estas alturas, la verificación de consistencia se realizará con la ayuda de un emparejamiento.

Dicho esto, vayamos directamente al asunto.

Preparando las Cosas

Nuestro esquema de compromiso consistirá en al menos tres pasos. El artículo en sí describe unos seis algoritmos, pero podemos acortar algunas cosas para hacer la explicación más digerible.

Para empezar, vamos a necesitar dos grupos de orden $n$: llamémoslos $\mathbb{G}_1$ y $\mathbb{G}_3$. También necesitaremos un generador para $\mathbb{G}_1$, que denotaremos por $G$. Estos grupos se generan de tal manera que existe un emparejamiento simétrico (o auto-emparejamiento) de la forma:

$$e: \mathbb{G}_1 \times \mathbb{G}_1 \rightarrow \mathbb{G}_3$$

Y esta será una pieza crucial del rompecabezas para nosotros.

Además, dado que estaremos tratando con polinomios, esta vez preferiremos la notación multiplicativa para representar los elementos de $\mathbb{G}_1$; esto es, el grupo tendrá la forma:

$$\mathbb{G}_1 = \{G^0, G^1, G^2, G^3, ..., G^{n-1}\}$$

Una nota importante: dado que $G$ será un input a un polinomio, y normalmente presentamos nuestros ejemplos con grupos de curvas elípticas, tenemos un problema: los puntos en una curva elíptica se multiplican por un escalar (es decir, $[s]G$), y no se elevan a una potencia.

Para aliviar este problema, podemos hacer uso de un isomorfismo en un grupo multiplicativo, con un razonamiento similar al explicado aquí.

Así que realmente, $G^s$ significará simplemente $[s]G$.

Bien, bien. Con esto realmente podemos empezar a preparar las cosas.

La Configuración

Ahora, este proceso funciona con lo que se conoce como una configuración de confianza. Para que funcione, el sistema debe ser inicializado, en el sentido de que algunos parámetros públicos deben ser calculados. Estos parámetros serán importantes durante el proceso de verificación.

Vamos a hacer un compromiso con un polinomio de grado como máximo $d$. Y para eso, esta es la configuración que necesitamos: un actor de confianza toma un entero aleatorio $\alpha$. Lo usa para calcular el siguiente conjunto de parámetros públicos:

$$p = (H_0 = G, H_1 = G^{\alpha}, H_2 = G^{\alpha^2}, ..., H_d = G^{\alpha^d}) \in \mathbb{G}^{d+1}$$

Y después de obtener estos valores, $\alpha$ debe ser descartado. El conocimiento de $\alpha$ permite que se forjen pruebas falsas — y es por eso que necesitamos confiar en quien realiza esta acción. Veremos cómo se podrían producir pruebas falsas más adelante.

Comprometiéndose al Polinomio

Ahora que todos tienen los parámetros públicos $p$, podemos crear el compromiso real.

Curiosamente, el compromiso será un único valor funcional:

$$\tilde{f} = G^{f(\alpha)} \in \mathbb{G}$$

Usaremos la notación de tilde ($~$) para denotar compromisos con funciones. Por ejemplo, $\tilde{f}$ representa un compromiso con $f$.

Al examinar más de cerca, podemos ver que se requiere $\alpha$ para calcular el compromiso. Pero en teoría, ¡α ha sido descartado en este punto! Entonces, ¿cómo podemos calcular esto?

¿Recuerdas los parámetros públicos calculados durante la configuración? Aquí es donde resultan útiles. Dado que nuestro polinomio tiene la forma:

$$f(x) = a_0 + a_1x + a_2x^2 + ... + a_dx^d$$

Lo que podemos hacer es producir el siguiente producto, utilizando los parámetros públicos:

$$S = {H_0}^{a_0}.{H_1}^{a_1}.{H_2}^{a_2}....{H_d}^{a_d} = \prod_{i=0}^d {H_i}^{a_i}$$

Si desarrollamos un poco la expresión:

$$S = G^{a_0}.G^{\alpha.a_1}.G^{\alpha^2.a_2}....G^{\alpha^d.a_d} = G^{a_0 + a_1.\alpha. + a_2\alpha^2 + ... + a_d.\alpha^d} = G^{f(\alpha)}$$

¡Y ahí lo tienes! Sin conocimiento de $\alpha$, todavía somos capaces de calcular nuestro compromiso. Este valor es calculado por el probador, y enviado al verificador, quien almacenará este valor, y lo usará más tarde cuando tenga que verificar que las evaluaciones adicionales del polinomio son correctas.

¡Veamos cómo!

Evaluación

Con el conocimiento del compromiso, podemos solicitar evaluaciones del polinomio secreto. Refiriéndonos a nuestro esquema original del proceso, esto significa que un verificador quiere conocer el valor del polinomio secreto $f(x)$ en algún entero específico $b$, por lo que realmente solicita el valor $f(b)$:

$$f(b) = a_0 + a_1b + a_2b^2 + ... + a_db^d$$

El probador puede simplemente calcular esto y enviarlo al verificador, pero el verificador necesita asegurarse de que el cálculo sea correcto y consistente, y que no está recibiendo un valor aleatorio y sin sentido.

Así que, junto con el valor $f(b)$, el probador deberá producir una prueba corta que el verificador pueda comprobar contra el compromiso que tiene.

Click to zoom

Veamos cómo se produce la prueba.

La Prueba

Reiterando rápidamente el objetivo, queremos probar que $f(b)= v$. Reorganizando un poco las cosas, también es cierto que:

$$f(b) - v = 0$$

Y esto significa que $b$ es una raíz de este polinomio:

$$\hat{g}(x) = f(x) - v$$

Con este simple cambio de perspectiva es lo que finalmente nos permitirá producir la prueba requerida.

Gracias al teorema del factor, sabemos que $\hat{g}$ puede ser perfectamente dividido (sin resto) por el polinomio $(x - b)$. Podemos calcular el polinomio cociente $p(x)$, que es el polinomio que satisface:

$$p(x)(x - b) = \hat{g}(x) = f(x) - v$$

Lo que sucede a continuación es que se calcula un compromiso con $p(x)$; esto se hace exactamente como lo hicimos con $f(x)$: usando los parámetros públicos. Y este compromiso será la prueba corta que necesitábamos. Así que nuestro diagrama anterior puede actualizarse así:

Click to zoom

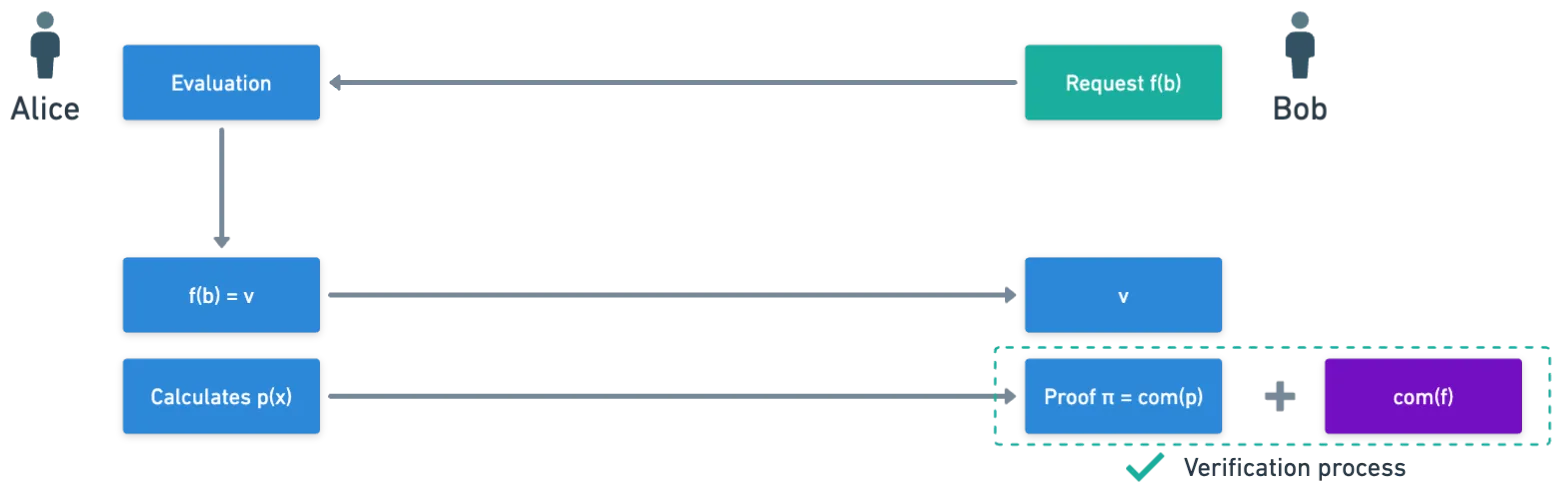
Al recibir la evaluación del polinomio $v$ y el compromiso con $p(x)$, el verificador puede comprobar que estos dos valores tienen sentido. Y aquí es donde las cosas se ponen interesantes.

¿Todo bien hasta ahora? Me tomó varias lecturas entender completamente la idea — recomiendo tomarlo con calma si es necesario.

Y spoilers: esta próxima parte podría ser un poco más pesada de lo habitual. Oh, vaya. Abróchate el cinturón.

Verificación

En términos simples, el verificador solo aceptará la evaluación si la siguiente validación resulta ser verdadera:

$$\tilde{p}^{\alpha - b} = \tilde{f}.G^{-v}$$

Hay un problema obvio aquí: $\alpha$ fue descartado, por lo que es desconocido. Veremos cómo evitar este problema en un momento. Pero primero, asegurémonos de que esta expresión tenga sentido.

Recuerda lo que son los compromisos: dado un polinomio $f$, es simplemente el valor:

$$\tilde{f} = G^{f(\alpha)} \in \mathbb{G}$$

Y ya vimos cómo calcular esto usando los parámetros públicos. Si introducimos esto en la expresión de validación, obtenemos:

$${\left ( G^{p(\alpha)} \right )}^{\alpha - b} = G^{f(\alpha)}.G^{-v}$$

Comprobando solo los exponentes, vemos que:

$$p(\alpha)(\alpha - b) = f(\alpha) - v$$

Por supuesto, si $p(x)$ se calculó correctamente y se evaluó, sabemos que las expresiones $(\alpha - b).p(\alpha)$ y $(f(\alpha) — v)$ deberían coincidir. ¡Así que el procedimiento de verificación tiene sentido!

Es aquí donde podemos visualizar claramente por qué el conocimiento de $\alpha$ permite la falsificación de pruebas.

Verás, podría enviarte algún número arbitrario $A$ en lugar de $f(\alpha)$ como el compromiso inicial, y no tendrías forma de saber que no es legítimo. Luego, como conozco $\alpha$, podría elegir algún $v$ arbitrario y convencerte de que $f(b) = v$ simplemente calculando directamente y enviándote el valor $P$:

$$P = \frac{A - v}{\alpha - b}$$

Y lo peor es que nunca tendrías ni la más mínima pista de que las pruebas son falsas. Así que sí, ¡es importante que $\alpha$ sea descartado!

En conclusión, $\alpha$ sigue siendo desconocido. ¿Qué podemos hacer al respecto?

La Magia de los Emparejamientos

Y aquí, amigos míos, es donde entran los emparejamientos. Simplemente presentaré cómo funciona el proceso, y comprobaremos que tiene sentido. ¡No es necesario tener mucha más motivación que esa!

Para introducir algo de terminología que usaremos a partir de ahora, llamemos al compromiso con $p(x)$ — que está relacionado con el valor $b$ —, un testigo. Y denotémoslo por $w(b)$:

$$w(b) = G^{p(\alpha)} = G^{\frac{f(\alpha) - f(b)}{\alpha - b}}$$

Ahora, la idea es que necesitamos verificar que este valor es consistente con el compromiso con $f$. Y para esto, necesitaremos evaluar nuestro emparejamiento, y comprobar:

$$e(w(b), G^{\alpha}.G^{-b}).e(G,G)^{f(b)} = e(\tilde{f}, G)$$

Woah woah woah. Un momento, Toretto. ¿Qué?

Bien. Tratemos de darle sentido a esto.

La esencia del asunto es que ambas evaluaciones producirán el mismo resultado solo si $w(b)$ está correctamente calculado. Y solo puede estar correctamente calculado si el probador realmente conoce el polinomio secreto.

Recuerda que la notación exponencial para elementos del grupo realmente significa multiplicación de puntos de curva elíptica (por escalar).

Formalmente, podemos ver que la igualdad se mantiene porque, usando la propiedad de bilinealidad de un emparejamiento:

$$e(w(b), G^{\alpha}.G^{-b}).e(G,G)^{f(b)} = e(G^{p(\alpha)}, G^{\alpha - b}).e(G,G)^{f(b)}$$ $$e(G,G)^{p(\alpha)(\alpha - b)}.e(G,G)^{f(b)} = e(G,G)^{p(\alpha)(\alpha - b) + f(b)}$$ $$e(G,G)^{f(\alpha)} = e(G^{f(\alpha)},G) = e(\tilde{f}, G)$$

Tómate un minuto. Léelo de nuevo. Deja que se asiente.

Si compruebas todos los parámetros en la expansión anterior, verás que los elementos en la explicación "más simple" que vimos primero se mezclan en la evaluación del emparejamiento.

Además, observa que hacemos uso de $G$ y $G^{\alpha}$. Estos valores se proporcionan en los parámetros públicos, y de hecho son los dos primeros valores: $H_0$ y $H_1$. ¡Así que esos son todos los parámetros públicos que vamos a necesitar para realizar la validación!

Fantástico, ¿no es así?

Resumen

Reconozco que este artículo no fue en absoluto simple de seguir. Los 10 minutos estimados de duración probablemente se sintieron como una estafa. Lo siento por eso. ¡Hice mi mejor esfuerzo para mantenerlo simple!

Para una visión diferente y más interactiva, sugiero consultar esta conferencia de Dan Boneh. No cubre la verificación de emparejamiento, pero prácticamente todo lo demás está incluido allí.

Así que, como se mencionó al principio del artículo, esta construcción por sí sola no parece ofrecer aplicaciones interesantes de inmediato. Sin embargo, vamos a usar esto como base para otras construcciones — en particular, para construir una familia de pruebas de conocimiento (cero) poderosas: SNARKs.

Sin embargo, ese no será nuestra próxima parada en la serie. En cambio, hablaremos de un tipo diferente de pruebas de conocimiento cero en el próximo artículo: Bulletproofs. Esto nos preparará naturalmente para pasar luego a los SNARKs. ¡Hasta la próxima vez!