Criptografía 101: STARKs
Este artículo forma parte de una serie más larga sobre criptografía. Si este es el primer artículo con el que te encuentras, te recomiendo encarecidamente comenzar desde el principio de la serie.
Pasamos cuatro artículos completos hablando sobre SNARKs — así que a estas alturas, deberíamos estar muy familiarizados con las ideas importantes detrás de esos frameworks. Principalmente, la concisión (coloquialmente, brevedad) de las pruebas es muy atractiva. También está el hecho de que son muy generales porque se basan en circuitos aritméticos para construir declaraciones.
Pero tienen un par de pequeños problemas que quizás debamos preocuparnos. Tratar de evitar estos problemas es una de las motivaciones para adentrarnos en el tema del artículo de hoy: STARKs.
Aviso
Evitaré entrar en demasiados detalles en algunas de las ideas detrás de los STARKs aquí. Va a ser bastante intenso tal como está... Pero siento que es un buen punto de partida. ¡Considera este artículo como una base sólida para que continúes explorando por tu cuenta, como siempre!
¿Qué es un STARK?
Esta vez, el acrónimo significa Scalable Transparent ARguments of Knowledge (Argumentos Escalables y Transparentes de Conocimiento).
¿Escalable? ¿Transparente? ¿Qué significan estos términos? Hagamos un rápido ejercicio de comparación para entender mejor estos conceptos.
SNARKs vs STARKs
Supongo que hay dos puntos principales a considerar aquí. Primero, está el hecho de que los SNARKs requieren una configuración de confianza.
Como recordatorio, una configuración de confianza es aquella donde algún actor necesita generar algunos parámetros públicos y descartar un valor secreto en el proceso. Si dicho valor secreto no se descarta, entonces podrían crear pruebas falsas en cualquier momento, ¡lo cual es ciertamente un gran riesgo!
Las configuraciones de confianza pueden realizarse con el máximo cuidado, pero aún así, siempre existe la posibilidad persistente de que los valores secretos no fueron descartados, lo que realmente socava cualquier protocolo que hayamos creado. Debido a esto, a veces incluso se les llama residuos tóxicos.
En contraste, los protocolos Transparentes no requieren ninguna configuración. En consecuencia, eliminan la amenaza silenciosa que representan las configuraciones de confianza. Suena interesante, ¿verdad?
Por otro lado, está el asunto de la escalabilidad, que es un término que ni siquiera hemos mencionado al hablar de SNARKs. Hay algo que no discutimos sobre ellos: ¿cómo sabe un verificador qué verificar?
La respuesta es que se les permite leer el circuito aritmético que se está utilizando. Puedes imaginar cómo esto toma un tiempo creciente a medida que el circuito se hace más grande — de hecho, toma tiempo lineal. Y los circuitos pueden volverse realmente grandes. Así que esto puede ser un gran no no.

Los STARKs intentan aliviar este problema adoptando un enfoque diferente. Los cálculos no se modelan como circuitos aritméticos, sino como una función de transición de estado en su lugar, y esto permite un tiempo de verificación más rápido en las circunstancias adecuadas. Analicemos eso con más detalle.
Funciones de Transición de Estado
Después de todo, los circuitos aritméticos son solo una forma de representar un cálculo. Existen otras estrategias para lograr el mismo propósito.
Imaginemos que tenemos algún cálculo que puede representarse como una serie de pasos. Comienzas desde algún estado inicial y aplicas una única función una y otra vez, hasta que alcanzas un estado final. Así:
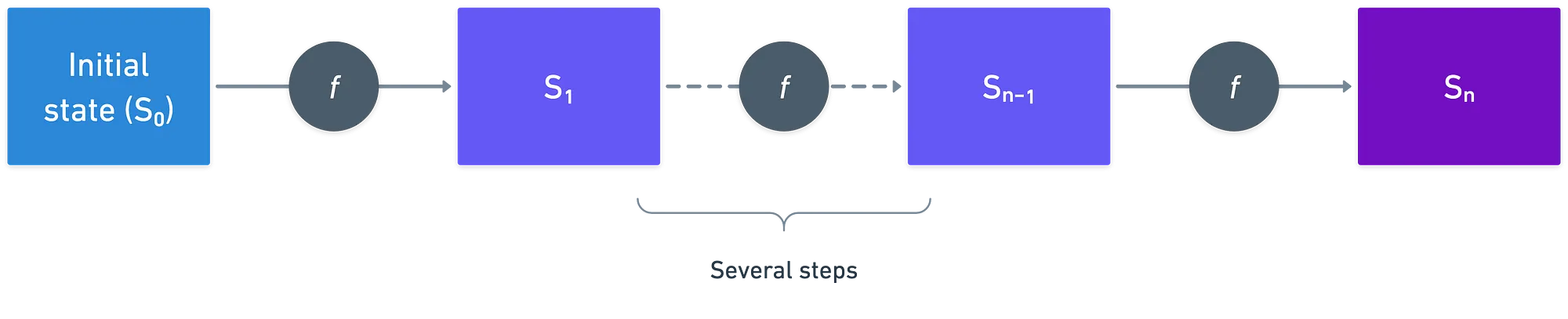
Todo el cálculo está impulsado por esta única función — esto es, una función de transición de estado. Nada nos impide escribir un circuito aritmético para representar el mismo cálculo — pero observa que tal circuito sería mucho más grande que la función de transición de estado, que solo representa un paso. En consecuencia, leer el primero toma mucho más tiempo que leer el segundo.
Y esta es la razón por la que los STARKs tienen escalable en su acrónimo: los verificadores pueden ejecutarse en tiempo sublineal.
Entonces, ¿qué es esta función de transición de estado, formalmente? Es simplemente una función de esta forma:
Donde el estado está representado por un vector de longitud , que por supuesto está compuesto de elementos de algún campo finito. Cada estado se calcula a partir del anterior:
Todo lo que nos importa es verificar que un cálculo sea correcto. O, refiriéndonos de nuevo a nuestro análisis sobre Plonk, verificar que una traza de cálculo satisfaga un conjunto de restricciones. En este caso, ¡la restricción siempre está dada por la misma función de transición de estado!
Nuestra traza de cálculo se verá como una tabla con columnas y filas, que representan todos los estados por los que pasamos:
| estado inicial () | 1 | 1 |
| paso 1 () | 2 | 3 |
| paso 2 () | 5 | 8 |
| paso 3 () | 13 | 21 |
| paso 4 () | 34 | 55 |
| paso 5 () | 89 | 144 |
Puede que reconozcas esto — ¡es la secuencia de Fibonacci! Podemos seguir aplicando la misma función de transición de estado una y otra vez para seguir generando números en la secuencia.
Codificación del Cálculo
Por supuesto, el siguiente paso tiene que ver con codificar esta traza, para que después un verificador pueda comprobar que las restricciones — dadas por la función de transición de estado — se cumplen. El proceso para hacerlo se llama aritmetización.
En Plonk, también realizamos una aritmetización. La técnica específica se llama en realidad aritmetización PLONKish.
Para codificar esta transición de estados, utilizaremos una técnica llamada Representación Intermedia Aritmética, o AIR para abreviar (por su sigla en inglés). Este algoritmo con nombre elegante funciona como un proceso de dos pasos:
- Codificar cada columna de la traza como un polinomio.
- Construir polinomios de restricción.
En este punto de la serie, estamos muy familiarizados con el primer paso. Todo lo que se necesita es asignar los valores en cada fila a algún valor de entrada índice (que representa el paso) de esta manera:
Esto es, el componente del estado, en el paso
Como en los SNARKs, el paso no es realmente un entero, sino una raíz de la unidad! Así que, realmente pertenece al conjunto:
Naturalmente, obtendremos polinomios, uno para cada columna — se llaman los polinomios de traza (de ahí el uso de para denotarlos). Y, por supuesto, los obtenemos mediante interpolación.
La segunda parte implica codificar la propia función de transición de estado. Al examinarla más de cerca, veremos que está compuesta por funciones individuales, una para cada componente del estado:
Cada una de estas componentes de función necesita ser escrita como una restricción, utilizando los polinomios de traza. Examinemos nuestro ejemplo de Fibonacci como ejercicio. Es fácil ver que la función puede expresarse como:
Basándonos en esto, podemos definir estos polinomios, que deberían evaluar a en las raíces de la unidad:
Recuerda que multiplicar por nos mueve al siguiente paso!
Así, si un verificador puede consultar los valores de los polinomios de traza en y , debería poder comprobar que las expresiones realmente evalúan a , lo que asegura que el cálculo satisface la función de transición de estado!
Si un verificador tuviera estos polinomios de restricción, simplemente podría ejecutar la comprobación mencionada anteriormente. Pero nunca realmente obtienen estos polinomios, por razones que discutiremos más adelante. Lo que sabemos por ahora es que los polinomios de restricción pueden derivarse de los polinomios de traza — así que imaginemos que esto se hace para reducir la redundancia, por ahora.
Bien, tenemos nuestra traza codificada. Hay alguna manipulación adicional que debe ocurrir — pero hablaremos de eso más tarde. Al igual que en Plonk, la codificación es necesaria para que podamos crear un marco en el que un verificador pueda consultar algunos valores y realizar algunas comprobaciones.
¿Te suena? Sí, necesitaremos una Prueba Oráculo Interactiva.

Volviendo a la Codificación
Ahora que sabemos cómo un verificador comprobaría la corrección de un cálculo en el contexto de los STARKs, y cómo se comprometen los valores polinomiales, podríamos diseñar una primera iteración de un sistema de prueba con solo estas piezas. Funcionaría así:
- el probador se compromete con los polinomios de traza
- el verificador lee la función de transición de estado, y luego solicita aperturas (a través de la IOP) para comprobar que las restricciones se cumplen
¡Oh, si solo fuera tan simple!
Veamos cómo un probador podría engañar en tal marco. Momentos divertidos nos esperan.

Supongamos que somos un probador malicioso, lo que significa que queremos convencer a un verificador de que una traza inválido es correcta. Y digamos que nuestra traza tiene pasos.
Por cualquier razón, digamos que manipulamos la traza en algún paso — haciendo que haya una única transición de estado inválida, mientras que todas las demás son correctas. ¿Qué probabilidad tiene un verificador de consultar esa transición de estado en particular?
Es bastante obvio que la respuesta es que tienen una probabilidad de entre de consultar exactamente la transición de estado inválida. Incluso si hacen múltiples consultas, las probabilidades realmente no suman mucho, especialmente cuando es grande.
¡Esto no parece muy seguro! ¿Qué podemos hacer para mejorar esta situación?
Mejorando la Seguridad
Nuestra estrategia será similar a la prueba de cero que usamos en Plonk. ¡Así que recomiendo consultar eso primero, si aún no lo has hecho!
Los propios polinomios de traza no codifican la restricción de la transición de estado — los polinomios de restricción lo hacen. Lo que necesitamos es manipularlos de una manera que nos permita comprobar la consistencia global a lo largo de la traza. Suena genial, ¿verdad?
Así que primero necesitaremos construir los polinomios de restricción. Estos dependen de nuestra función de transición de estado — recordando nuestro ejemplo de Fibonacci, se veían así:
En este ejemplo simple, los polinomios de restricción tienen grado a lo sumo . Pero es totalmente posible que tengan grado mayor que , porque la función de transición de estado puede muy bien contener multiplicaciones.
Ya hemos mencionado cómo estos polinomios tienen raíces en las raíces de la unidad — esto es, el dominio de evaluación . Estos valores pueden usarse para construir un polinomio conocido como el anulador o polinomio de anulación:
Como estamos usando las raíces de cada , cuando dividimos los por , obtenemos otro polinomio de grado menor, sin resto:
Naturalmente, llamaremos a estos los polinomios cociente.
¿Qué tienen de tan interesante, podrías preguntar? La respuesta es muy elegante: si alteramos la traza aunque sea un poco, entonces los polinomios de restricción originales no serán divisibles por , lo que significa que quedará algún resto. Y en consecuencia, si muestreamos algún valor aleatorio , y encontramos que:
Entonces es altamente probable que sea de hecho divisible por , lo que significa que satisface las restricciones de transición de estado.
¡No me digas que eso no es bonito!
Sin embargo, hay algo a considerar: si muestreamos del conjunto , entonces tanto como siempre darán , lo que significa que nos quedamos con:
Y en este caso, podría ser cualquier cosa. En consecuencia, realmente no estamos comprobando la igualdad polinomial aquí.
Los STARKs superan este problema expandiendo el dominio de evaluación. Esto es, al verificador se le permite muestrear de un dominio más grande . La relación de los tamaños de y tiene un nombre especial — se llama el factor de expansión. Su valor generalmente está en algún lugar entre y .
Al evaluar tanto como los en los nuevos puntos añadidos en , ninguno dará cero. Y así, en este dominio expandido, nuestra comprobación original realmente nos permite verificar la igualdad polinomial.
Por cierto, no creo que haya mencionado esto antes, pero este tipo de comprobación tiene un nombre: es el lema de Schwartz-Zippel en acción. Lo usamos sin mencionarlo en el artículo de Plonk también!
¡Este es un gran progreso! Tristemente, no es suficiente.

Hay formas sutiles de engañar a través de estas nuevas medidas de seguridad — para las cuales querremos realizar otra comprobación.
Creo que este artículo se está haciendo bastante largo. ¡Ahora es un buen momento para una pausa para tomar café!
Rompiendo el Sistema
Intentemos engañar, de nuevo.
Supongamos que modificamos el valor de la traza en algún paso . Pero en lugar de interpolar solo la traza, añadimos más valores a la interpolación.
Al calcular los polinomios de restricción, ocurrirán dos cosas:
- No evaluarán a cero en el(los) paso(s) que fueron manipulados,
- Tendrán grado más alto de lo esperado.
Nuestra estrategia para detectar actividad maliciosa es evaluar:
Dentro del dominio de evaluación , esta comprobación fallará para el(los) paso(s) que fue(ron) modificado(s), pero pasará para todos los demás. El problema es lo que sucede fuera de , en el dominio expandido .
Allí, el polinomio de anulación evaluará a algún valor no cero. Así que, mientras podamos crear polinomios y de alto grado que coincidan con la condición anterior... Estamos esencialmente de vuelta al punto de partida.
El problema es similar a nuestro problema original, pero ligeramente peor: hay una probabilidad de entre (el tamaño de ) de muestrear exactamente el valor donde la comprobación no se cumple. Así que podría decirse que es peor porque es más grande que .
En resumen: ¡estamos en problemas!
¡Y eso es todo! El sistema que tan cuidadosamente hemos construido hasta ahora ha sido engañado.

Gran (pero extremadamente extraña) película, por cierto.
Afortunadamente, hay una manera inteligente de defenderse de este tipo de ataque.
Verás, la única forma en que un probador malicioso puede hacer el proceso que describimos es creando polinomios de traza con grado más alto de lo esperado. Y si conocemos la longitud de la traza, sabemos qué grado esperar.
Así que esa es nuestra solución: comprobar que algunos de estos polinomios tienen grado bajo. Y eso atará todo.
Como sutileza: en KZG, no necesitamos este tipo de comprobación porque el grado del polinomio está codificado en los parámetros públicos. Esencialmente, el grado no es algo con lo que un atacante pueda jugar.
Comprobando Grado Bajo
Ahora, esta es la verdadera razón por la que elegimos FRI. Veamos cómo funciona.
Utilizaremos los polinomios cociente. Queremos comprobar que su grado es como máximo , donde puede calcularse conociendo tanto la función de transición de estado como el número de pasos en la traza.
La estrategia que aplicaremos se llama dividir y plegar. La idea aproximada detrás de esto es separar una afirmación (en este caso, que las evaluaciones corresponden a un polinomio de grado bajo) en dos afirmaciones de la mitad del tamaño, que se combinan con alguna entrada imprevisible del verificador. La mejor manera de entender esto es verlo en acción.
Nuestro polinomio tiene grado como máximo , así que podemos representarlo de esta manera:
Los son simplemente los coeficientes del polinomio. Podemos dividir esto en sus potencias pares e impares, así:
Donde:
Puede llevarte un momento entender esto. Tómate tu tiempo.
Si prestaste mucha atención a las expresiones anteriores, notarás que puede no ser un entero, lo cual es un problema. El protocolo utiliza un truco interesante para asegurar que este sea el caso, pero no lo cubriremos aquí.
Estos dos polinomios tienen la mitad del grado del original.
A continuación, se le pide al verificador un entero aleatorio . Y los dos polinomios se condensan en uno nuevo, con la mitad del grado (de ahí el plegado, como en plegar por la mitad), así:
Con el conocimiento de , podemos construir la palabra código (es decir, evaluaciones) para este nuevo polinomio . No entraré en todos los detalles de cómo sucede esto, pero puedes imaginar que es solo cuestión de hacer algunas sustituciones aquí y allá. Este artículo entra en todos los detalles si estás interesado.
El resultado de este proceso es una palabra código (de nuevo, evaluaciones) del polinomio reducido, en un dominio que es la mitad del tamaño, al cual el probador se compromete.
En este punto, el verificador tiene ambos compromisos con y , y el valor muestreado . Su objetivo es comprobar que ambos polinomios son consistentes — lo que significa que esta relación aquí debería mantenerse:
¡Te dejo a ti comprobar que esto debería mantenerse! Es bastante sencillo.
Esto se hace a través de una comprobación de colinealidad, que no cubriremos esta vez.
Realmente, hay muchos matices, optimizaciones y detalles para cubrir para que tengamos una comprensión completa de los STARKs. Me contento con capturar las ideas principales del protocolo en este humilde artículo, pero debes saber que hay más para que explores si estás interesado.
Una vez que el verificador comprueba que la relación entre polinomios es correcta, el proceso simplemente se repite, usando como el nuevo punto de partida. Y después de suficientes rondas, el probador terminará con una constante, que envían al verificador, ¡dejando claro que han terminado de plegar la palabra código original!

Eso fue mucho, y siento que apenas hemos arañado la superficie. Aún así, es suficiente para entender esto: el número de rondas en este proceso de reducción nos permite establecer una cota superior para el grado del polinomio con el que comenzamos!
Y así, este proceso nos permite demostrar que un polinomio tiene algún grado acotado, que como vimos anteriormente, es importante para asegurar tanto que la traza original no fue manipulada, como que la comprobación de consistencia es realmente significativa.
Volviendo a las IOPs
Cuando exploramos Plonk, vimos cómo las Pruebas Oráculo Interactivas (IOPs) eran una forma para que un verificador consultara evaluaciones específicas de polinomios — o solicitara aperturas en puntos específicos. Con dichas aperturas, pueden verificar algún tipo de afirmación alrededor de dichos polinomios.
Por ejemplo, en Plonk, vimos cómo podíamos construir IOPs para comprobar que un polinomio es cero en un conjunto dado.
Haremos básicamente el mismo proceso. La idea es que un verificador no necesita comprobar cada restricción de transición, sino que puede quedar satisfecho comprobando solo algunas muestras aleatorias, para las cuales solicitará aperturas.
Aunque, para los STARKs, no usaremos la misma IOP que usamos para Plonk. En su lugar, usaremos algo llamado Prueba Oráculo Interactiva de Proximidad Reed-Solomon Rápida, o FRI para abreviar.

Buenas noticias, sin embargo — esta técnica de nombre elegante utiliza un ingrediente principal, que ya hemos cubierto en la serie: árboles de Merkle!
Las Pruebas Oráculo Interactivas generalmente requieren un esquema de compromiso. Así que primero describiremos cómo funciona el esquema de compromiso para FRI.
Dado algún polinomio , podemos elegir algún dominio de evaluación , que es solo un conjunto de valores de que usaremos para producir valores de :
Evaluar en simplemente produce otro conjunto de valores, a saber:
Este conjunto a veces se denomina palabra código Reed-Solomon. Y lo que haremos con él es ponerlo en un árbol de Merkle. Al calcular la raíz del árbol, lo que obtenemos es esencialmente un compromiso con todas estas evaluaciones de . ¡Genial!
Usar una estructura de árbol de Merkle nos permite realizar un protocolo de ida y vuelta (sigma) que permite a un verificador solicitar valores del polinomio secreto y comprobar que son correctos (o al menos, consistentes con el compromiso). Esto se hace a través de pruebas de Merkle, a veces también denominadas caminos de autenticación.
¿Por qué Árboles de Merkle?
Cuando comparamos esto con otros esquemas de compromiso, como el esquema KZG, podemos ver que hay algunas diferencias clave que se alinean bien con nuestras necesidades.
La primera diferencia clave se relaciona con la transparencia. Verás, los esquemas de compromiso basados en árboles de Merkle no requieren ninguna configuración. En comparación con otros métodos, alivia la posibilidad de que los parámetros secretos no sean descartados, lo que es una amenaza para la seguridad de cualquier sistema de prueba.
En segundo lugar, debemos considerar la escalabilidad y la eficiencia. Los árboles de Merkle son muy eficientes cuando manejan grandes cantidades de datos — las pruebas son logarítmicas en tamaño debido a la estructura del árbol, como hemos mencionado anteriormente. Esquemas como KZG son lineales respecto al número de entradas, lo que hace que su escalabilidad no sea tan buena. Además, los datos comprometidos son simplemente evaluaciones polinomiales en un campo finito, que son operaciones baratas en comparación con las operaciones de grupo de curva elíptica, utilizadas por KZG.
También podríamos estudiar las suposiciones criptográficas alrededor de nuestro método. Digamos simplemente que el ingrediente principal para las estructuras basadas en árboles de Merkle son las funciones de hash, en contraste con los emparejamientos en el caso de KZG. Actualmente no se sabe cómo evolucionará la seguridad de los métodos basados en emparejamientos con la llegada de la computación cuántica (¡más sobre esto en artículos posteriores!), mientras que se piensa que las funciones de hash son más robustas en ese entorno.
¡Bien, perdón por el exceso de información! El TL;DR de esto es:
![]()
![]() Usamos árboles de Merkle como nuestro esquema de compromiso porque es adecuado para nuestro caso de uso, por razones de transparencia, escalabilidad y eficiencia.
Usamos árboles de Merkle como nuestro esquema de compromiso porque es adecuado para nuestro caso de uso, por razones de transparencia, escalabilidad y eficiencia.![]()
![]()
Sin embargo, hay más en FRI. Los árboles de Merkle son solo una pieza del rompecabezas. Por ahora, volvamos a nuestros polinomios.
Resumen
Hemos profundizado bastante en el funcionamiento interno de los STARKs.
Juntando todas las piezas, el protocolo tiene aproximadamente estos pasos:
- El probador aritmetiza la traza de cálculo en polinomios de traza, y calcula los polinomios de restricción y cociente,
- El probador luego se compromete con los polinomios de traza y cociente a través de árboles de Merkle,
- El verificador solicita algunas aperturas para comprobar que los polinomios cociente son consistentes,
- Finalmente, FRI se utiliza para asegurar que los polinomios cociente tienen grado acotado.
Los polinomios de traza son necesarios para las comprobaciones de restricciones de límite, que no cubrí. ¡Solo debes saber que son necesarios para garantizar que los estados inicial y final del cálculo son correctos!
Si todo está en orden, entonces el verificador acepta la prueba.
Es difícil reducir la complejidad de los STARKs a una explicación simple. Algunos de los conceptos que hemos cubierto son bastante complicados, pero en su núcleo, todo lo que estamos usando son elementos y técnicas simples, orquestados de manera compleja para producir resultados asombrosos.
Y, como con cualquier sistema criptográfico complejo, siempre hay más por explorar. Para material introductorio adicional, consulta este artículo complementario. También, sugiero fuertemente leer esta serie de artículos para una mirada mucho más profunda a los STARKs — ¡pero incluso entonces, encontrarás que algunos detalles se omiten!
Es así de complicado, sí.
Realmente espero que este artículo haya proporcionado algunos fundamentos sólidos del marco general de los STARK. La criptografía continúa evolucionando, pero aprender las ideas detrás de estas técnicas es siempre un gran ejercicio para mantenerse mejor al día con lo que está por venir en el futuro.
Dicho esto, nuestra próxima parada en la serie nos acercará un paso más a un tema que es muy debatido en la escena criptográfica actual: la Criptografía Post-Cuántica, o PQC. La mayoría de los métodos en esta área se basan en una estructura matemática que aún no hemos cubierto: los Anillos. Y ese será el tema para nuestro próximo encuentro. ¡Hasta pronto!

¿Te resultó útil este contenido?
Apoya a Frank Mangone enviando un café. Todos los ingresos van directamente al autor.
