Criptografía 101: Criptografía Post-Cuántica

Este artículo forma parte de una serie más larga sobre criptografía. Si este es el primer artículo con el que te encuentras, te recomiendo comenzar desde el principio de la serie.

Ahora que hemos cubierto la teoría básica sobre el problema de aprendizaje con errores en anillos y los retículos ideales, el siguiente paso natural es ponerlos en práctica.

En 2016, el Instituto Nacional de Estándares y Tecnología de EE.UU. lanzó una iniciativa llamada Proyecto de Estandarización de Criptografía Post-Cuántica. La idea era recibir nominaciones para algoritmos resistentes a la computación cuántica (más sobre esto en un momento) con la esperanza de seleccionar los mejores candidatos y estandarizar un conjunto de técnicas que podrían usarse para construir la próxima generación de una web segura.

Después de unos años, se anunciaron cuatro ganadores — y tres de ellos eran algoritmos basados en retículos.

En este artículo, veremos cómo funcionan algunos de estos algoritmos y también dedicaremos tiempo a discutir cómo las computadoras cuánticas amenazan los métodos criptográficos que protegen nuestras comunicaciones diarias.

Computación Cuántica en Resumen

No soy un experto en el campo de la mecánica cuántica en absoluto (aunque he tomado un curso o dos). Con mi conocimiento limitado, puedo decir que es un tema bastante complejo, e incluso es desafiante comprender algunas de las ideas más básicas y fundamentales. Esta es la razón por la que no entraremos en muchos detalles sobre cómo funcionan las computadoras cuánticas. Sin embargo, un pequeño repaso es necesario para entender por qué es importante preocuparse por su poder computacional.

Nuestras computadoras cotidianas operan usando corriente eléctrica, que esencialmente se usa para representar números binarios. Ya sabes, la corriente fluyendo indica un $1$, y la corriente sin fluir indica un $0$ — eso es lo que conocemos como un bit. Cada bit solo puede representar dos estados.

Además, las operaciones en las computadoras tradicionales se realizan secuencialmente, lo que significa que necesitas leer algunos bits de datos, realizar una operación (como una suma), almacenar los datos resultantes... Y solo entonces puedes pasar a la siguiente operación.

Esto ha funcionado abundantemente bien para la humanidad. Las computadoras son capaces de resolver todo tipo de problemas muy rápido, lo que ha ayudado a desarrollar muchas áreas del conocimiento.

Y también nos dieron Minecraft.

Pero, para algunas operaciones, estas simples limitaciones hacen que resolver algunos problemas sea absolutamente inviable. De hecho, de eso se trata la criptografía: crear rompecabezas lo suficientemente difíciles como para que nuestro poder computacional actual no pueda resolverlos en un tiempo razonable.

Las computadoras cuánticas están construidas de manera diferente. La unidad fundamental de información es el bit cuántico o qubit para abreviar. Un qubit puede existir en un estado que no es ni $0$ ni $1$. Existe en una superposición de ambos estados, lo que significa que es una combinación de estados.

Una posible analogía es una cuerda de guitarra vibrando. Mientras vibra, produce un sonido, por lo que su "estado" es muy real para nosotros. Pero, ¿cómo describimos matemáticamente dicha vibración? Bueno, podemos describirla como una combinación de diferentes patrones de vibración "simples" llamados modos de vibración.

Esto es lo que la superposición esencialmente hace: representar el estado actual como una suma ponderada de partes más simples. ¡Pueden ser infinitas partes, pero eso es aceptable!

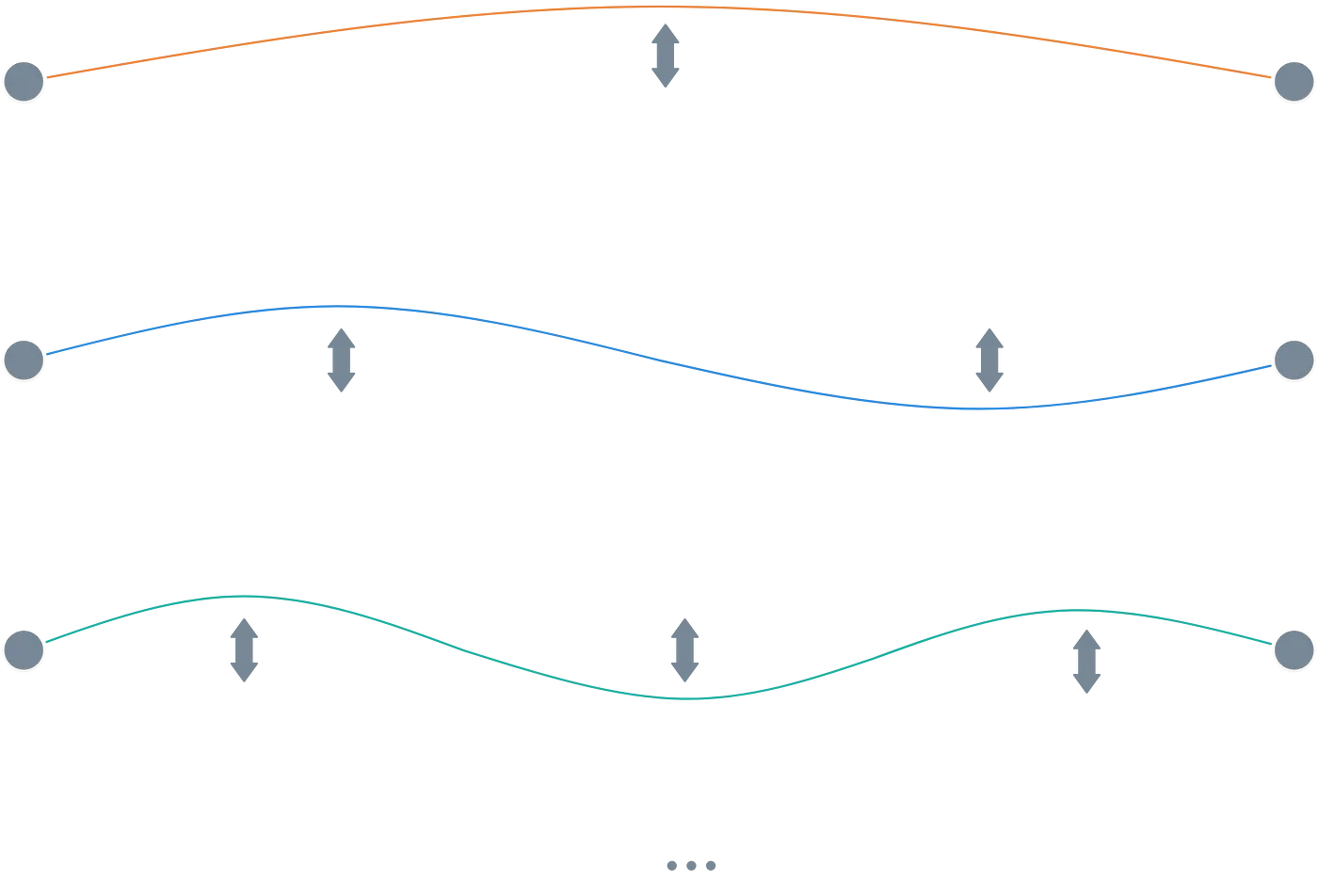
Debido a que un qubit codifica mucha más información que un simple $0$ o $1$, permite que múltiples operaciones se ejecuten al mismo tiempo. Y esto aumenta exponencialmente cuantos más qubits tengamos.

El resultado de esto (junto con un par de términos más extraños que ni siquiera hemos mencionado, como el colapso de la función de onda y el entrelazamiento) es una computación mucho, mucho más rápida. ¡Tanto que nuestros métodos actuales basados en curvas elípticas no tendrían muchas posibilidades!

Podríamos ejecutar el algoritmo de Shor y resolver rápidamente problemas como el de factorización de números primos.

Las computadoras cuánticas no son muy prácticas hoy en día — es poco probable que estés leyendo este artículo en una pronto. Pero nunca sabemos lo que el futuro puede deparar, y aunque las computadoras cuánticas no sean para uso cotidiano, instalaciones especializadas que las alberguen podrían resolver problemas complejos muy rápido y romper nuestros modelos de seguridad actuales.

En resumen:

Los métodos ECC actuales pueden ser descifrados con computadoras cuánticas, por lo que necesitamos algoritmos mejores y más seguros.

Esta es la razón principal por la que PQC ha sido un tema tan candente recientemente: intentar proteger la información de esta amenaza latente. Se cree que los problemas basados en retículos son tan difíciles que ni siquiera las computadoras cuánticas pueden resolverlos rápidamente.

Con esta promesa de robustez y seguridad, echemos un vistazo a dos de los algoritmos propuestos por NIST para estandarización. Pero antes de eso...

Generación de Claves

Ambos algoritmos compartirán la misma construcción para claves privadas y públicas. Esto es muy similar a la criptografía de curva elíptica, donde las claves casi siempre eran un entero grande $d$ (clave privada) y un punto $[d]G$ en la curva elíptica (clave pública).

Esta vez, sin embargo, las claves involucrarán anillos y basarán su seguridad en el problema RLWE que ya vimos en el artículo anterior.

¡Bien, suficiente preámbulo! Veamos cómo funciona esto.

Al igual que necesitas seleccionar una curva elíptica para cualquier método ECC (como ECDSA), necesitaremos seleccionar un anillo aquí y también algunos parámetros públicos para el sistema.

Primero, elegimos el anillo $R$, generalmente de la forma:

$$R = \mathbb{Z}_q[X]/(X^n + 1)$$

Luego, tomaremos muestras de varios polinomios aleatorios de él. Estos se colocarán en una matriz $k \times l$ que llamaremos $A$:

$$A \in R^{k \times l}$$

El par $(R, A)$ es similar al par $(E, G)$, donde $E$ es una curva elíptica y $G$ un generador. ¡No hay sorpresas aquí!

Con esto en mano, la generación de claves es bastante simple. Necesitamos alguna información secreta para nuestra clave privada — estos serán dos vectores de polinomios, uno de longitud $l$ y uno de longitud $k$.

$$\\ s_1 \in R^l \\ s_2 \in R^k$$

Tienen una particularidad, sin embargo — son polinomios cortos. En este contexto, corto se relaciona con la representación vectorial de cada polinomio, que, como recordarás, viene de usar los coeficientes como las coordenadas de un vector.

Para que un vector sea "corto", necesitamos que los coeficientes sean pequeños. Y así, para muestrear estos polinomios $s_1$ y $s_2$, también requerimos que los coeficientes sean pequeños, típicamente limitados a un rango $\{−\eta, ..., \eta \}$, donde $\eta$ es un entero pequeño.

¡Al igual que los polinomios o vectores de error!

Tenemos nuestra clave privada $(s_1, s_2)$. Con ellos, simplemente calculamos:

$$t = A.s_1 + s_2 \in R^k$$

La clave pública será simplemente $(A, t)$. ¡Observa que recuperar $s_1$ y $s_2$ a partir de $A$ y $t$ implica resolver el problema RLWE — lo que significa que podemos compartir la clave pública de manera segura!

Claves asimétricas, listo. Ahora podemos pasar a nuestros métodos de hoy.

Kyber

CRYSTALS Kyber es formalmente un Mecanismo de Encapsulación de Claves (KEM por sus siglas en inglés), lo que significa que es una forma para que un remitente transmita un mensaje secreto corto a través de una red de manera segura — y un receptor puede luego recuperar dicho secreto.

Es similar al cifrado pero generalmente se usa para un propósito diferente, como transmitir claves simétricas para su uso posterior en comunicaciones subsiguientes.

Esta técnica consiste en tres pasos bastante estándar: generación de claves, encapsulación (similar al cifrado) y desencapsulación (que es análogo al descifrado).

Afortunadamente, ya sabemos cómo funciona la generación de claves. Un receptor generará una clave privada $(s_1, s_2)$ y compartirá la clave pública asociada $(A, t)$ con el remitente del mensaje.

Con esto, podemos pasar directamente al segundo paso.

Encapsulación

Bien, esto comienza más o menos como esperarías que funcionara el cifrado: un remitente quiere compartir un valor $M$ con un receptor. Pero lo que sucede a continuación puede sonar bastante exótico para nosotros: transforman dicho valor en su representación binaria — y luego codifican los dígitos en un polinomio. No solo eso, sino que luego escalan ese polinomio por un factor de la mitad del tamaño del campo, redondeado.

Sí, probablemente fue mucho para asimilar. Creo que intentar visualizar esto nos ayudará a entender el proceso, así que continuemos con un ejemplo juguete.

Toma el número $13$. Su representación binaria es $1101$. De derecha a izquierda, si mapeamos cada dígito a una potencia de $x$, este es el polinomio que obtenemos:

$$x^3 + x^2 + 1$$

Luego, supongamos que estamos trabajando con módulo $19$. Necesitamos escalar este polinomio por un factor de la mitad de $19$, que, redondeado, resulta en $10$. Y así, nuestro valor $13$ se ha transformado en:

$$10x^3 + 10x^2 + 10$$

Lo sé, definitivamente no es lo que estamos acostumbrados — esta parte podría ser un poco confusa, pero prometo que tendrá sentido en un minuto.

Entonces, tenemos nuestro mensaje en forma polinómica — llamémoslo $m$. Lo que el remitente necesita hacer ahora es calcular el texto cifrado. Para esto, toman muestras de tres vectores aleatorios: $r$, $e_1$ y $e_2$, y realizan estas operaciones:

$$u = A^T.r + e_1$$ $$v = t^T.r + e_2 + m$$

El superíndice $T$ significa que tomamos la transpuesta de un vector o matriz.

Y el texto cifrado resultante es simplemente $(u, v)$. Esto se envía al receptor, quien procede a desencapsular.

Nota que podemos trazar algunos paralelismos con ECC aquí: $r$ es lo que usualmente llamamos un nonce, y necesitamos un valor para codificar el nonce ($u$) y el otro para codificar el mensaje junto con el nonce ($v$).

Desencapsulación

El paso final es muy directo, pero es en realidad donde encontramos la salsa secreta que hace que todo este lío funcione.

El receptor simplemente calcula:

$$m' = v - {s_1}^T.u$$

Haciendo las sustituciones y cancelaciones, lo que el receptor obtiene es:

$$m' = m + {s_2}^T.r + {s_1}^T.e_1 + e_2$$

Hmm... Eso es extraño. Normalmente, los procesos de descifrado devuelven el mensaje original, pero ese no es el caso aquí. ¿Qué está pasando? Parece que estamos en un aprieto. ¿Hemos llegado a un callejón sin salida?

¡Por supuesto que no! Verás, la diferencia entre $m$ y $m'$ es solo un montón de polinomios. Si son pequeños, entonces $m$ y $m'$ estarán muy cerca en valor. ¡Y porque aplicamos un escalado adecuado antes de enviar la información, entonces los coeficientes de $m'$ estarán cerca de $0$ o $10$!

¡Ayuda que elegimos $s_1$, $s_2$, $e_1$ y $e_2$ como polinomios pequeños! ¡Yay!

Así, para cada coeficiente, simplemente elegimos el que esté más cerca — $0$ o $10$. Finalmente, ¡revertimos el escalado dividiendo por $10$ y recuperamos el mensaje original!

Visualmente:

Click to zoom

Es bastante complejo, lo sé. Pero en esencia, no es muy diferente de otros métodos de cifrado: el remitente tiene algún tipo de clave pública, realiza un par de operaciones y envía algún texto cifrado que solo puede ser decodificado con la clave privada del receptor.

¡Lo bueno es que a medida que el campo y los tamaños de los polinomios se hacen más grandes, este problema se vuelve inimaginablemente difícil de resolver sin conocimiento de la información secreta. ¡Increíble!

Para más información sobre este método, sugiero leer este artículo o este otro, o ver este video:

Dilithium

Aparte del cifrado, solemos pensar en las firmas digitales como el otro tipo de operación primitiva en criptografía. Es lógico que este sea el siguiente tipo de algoritmo que nos gustaría tener en nuestra caja de herramientas PQC.

CRYSTALS Dilithium fue uno de los primeros algoritmos de este tipo. Es parte de la misma suite de algoritmos criptográficos a la que pertenece Kyber, llamada CRYSTALS. La generación de claves sigue siendo exactamente la misma que antes.

¡No hay mucho más que decir sobre esto, realmente! Vamos directo al grano.

Firma, Parte Uno

Firmar un mensaje $M$ requerirá algunos pasos. Dividiré esta sección en dos partes para mantener las cosas organizadas.

Comenzamos de una manera muy estándar: necesitamos elegir un nonce, como en otros algoritmos de firma. Esta vez, el nonce es un vector de polinomios cortos:

$$y \in R^l$$

Lo que viene después es un poco complicado. Necesitamos comprometernos con el nonce, al igual que lo hicimos en curvas elípticas con operaciones como $[k]G$. Más o menos lo mismo sucede al principio: calculamos $w = A.y$. Y luego, las cosas se ponen salvajes: ahora realizamos un paso de compresión.

Para entender qué sucede, enfoquémonos en una sola coordenada del vector polinómico $w$ — así que estamos mirando un solo polinomio $W(X)$. Sus coeficientes son números en un campo finito grande, por lo que pueden ser muchos números grandes, lo que significa que contribuirán a hacer que nuestra firma sea bastante grande. Y generalmente no queremos eso.

Por eso tiene sentido el paso de compresión. Para visualizarlo, imaginemos que tenemos algo como:

$$W(X) = 1054321X^3 + 562837X^2 + 7812312X + 2345235$$

La compresión funciona tomando algún número $2^d$ y realizando dos operaciones:

• Dividir cada coeficiente de $W(X)$ por $2^d$, y redondear hacia abajo. El resultado se llama los bits altos.
• Luego, calcular $\textrm{mod} \ 2^d$ para cada coeficiente de $W(X)$. Estos se llaman los bits bajos.

La nomenclatura puede parecer extraña al principio. ¡Pero todo tiene sentido cuando te das cuenta de que la representación binaria de $2^d$ es solo un $1$ seguido de $d$ ceros!

Y esto funciona muy bien al calcular las dos operaciones anteriores: dividir es lo mismo que desplazar los bits $d$ espacios a la derecha, y el módulo se puede calcular tomando los $d$ últimos dígitos de un número.

¿No me crees? Trabajemos un ejemplo juntos:

• Toma el número $37610278412$. Su representación binaria es $100011000001101111110100111000001100$ (ver aquí).
• Luego, elige una potencia que dé aproximadamente la mitad de los dígitos del número que seleccionamos antes. En este caso, usemos $17$. Entonces, $2^{17} = 131072$.
• Calculamos los bits altos como $⌊37610278412 / 131072⌋$, lo que da $286943$. La representación binaria es $1000110000011011111$.
• Finalmente, calculamos los bits bajos como $37610278412 \ \textrm{mod} \ 131072$, lo que da un resultado de $85516$; en binario, $10100111000001100$.

Y ahora, como por arte de magia:

Click to zoom

¡Bien, eso fue bastante! ¡Hagamos una pausa por un momento y apreciemos lo hermosamente simple que es este proceso!

En Dilithium, solo mantenemos los bits altos de cada coeficiente en el vector de polinomios $w$ — denotaremos este resultado $w_1$.

Si eres como yo, probablemente te sientas así en este punto del artículo:

¡Las buenas noticias son que estamos muy cerca de la meta! Toma un par de respiros profundos. Esto solo tomará unos minutos más.

Cuando estés listo, continuemos.

Firma, Parte Dos

Tenemos el compromiso comprimido del nonce — pero esa es solo la primera parte de la firma. Imagina que el firmante envía este compromiso al verificador, y en respuesta, el verificador envía algún desafío $c$, que es solo un polinomio pequeño con coeficientes $-1$, $0$ y $1$.

Con él, calculamos el valor final de la firma, que es:

$$z = y + c.s_1 \ \textrm{mod} \ q$$

Y la firma es simplemente la tupla $(z, w_1, c)$.

Hay un paso adicional importante de verificación de límites aquí, pero lo omitiremos en aras de simplificar un poco las cosas.

Ahora, es posible que hayas notado dos cosas: una, la firma no incluye el mensaje en ninguna parte, y dos, como lo describí, esto sería un protocolo interactivo, que es algo que no queremos.

Ya sabemos que usando la transformada de Fiat-Shamir, esto se puede convertir en un esquema de firma no interactivo mediante un hash. ¡Y al incluir el mensaje en la mezcla, se satisfacen todos nuestros requisitos!

Así que solo necesitamos calcular el hash (Dilithium usa un algoritmo de hash llamado SHAKE, parte de la familia SHA-3) del nonce comprimido y el mensaje original:

$$c = H(w_1, M)$$

Esto es solo un número binario, sin embargo — necesitamos convertirlo en un polinomio con coeficientes $-1$, $0$ y $1$. Para lograr esto, la técnica que usamos se llama muestreo por rechazo. Que, simplificando un poco, podría verse así:

• $00$ se mapea a $0$
• $10$ se mapea a $1$
• $01$ se mapea a $-1$
• $11$ no se considera válido, así que descartamos el valor y pasamos a los siguientes dos bits.

En realidad, este mapeo es un poco más complejo para asegurar que la mayoría de los coeficientes sean $0$.

El hash funciona como un muestreo de una distribución aleatoria de la que tomamos muestras, leyendo el flujo de datos 2 dígitos a la vez, generando un coeficiente de c en cada paso.

¡Genial! Nuestra firma está lista. ¿Cómo funciona la verificación?

Verificación

Recapitulación rápida: el verificador tiene una clave pública $(A, t)$ y ahora también tiene la firma $(z, w_1, c)$ del mensaje $M$.

Para verificar, solo necesitan calcular:

$$w' = A.z - c.t \in R^k$$

Sustituyendo el valor correcto de $z$ aquí obtenemos:

$$w' = A.y - c.s_2 \in R^k$$

Esencialmente, $w'$ será diferente del compromiso original $w$, pero la diferencia es solo un vector de polinomios pequeños $c.s_2$ — solo algo de ruido pequeño.

Otra forma de decir esto es que solo los bits bajos de los coeficientes polinómicos serán diferentes entre sí al comparar $w$ y $w'$, mientras que los bits altos deberían coincidir. ¡Mira eso! Nada menos que brujería.

¡El verificador solo necesita calcular los bits altos de $w'$ y comparar ese resultado con $w_1$. Si coinciden, se acepta la firma!

Nuevamente, la verificación de límites también es importante para prevenir falsificaciones, aprovechando completamente la dificultad del Problema del Vector Más Corto (SVP) en un retículo, pero omitiremos esa parte aquí.

El artículo original entra en detalle completo sobre esto. Y para una mirada alternativa a Dilithium, aquí hay otro artículo con una perspectiva ligeramente diferente.

Resumen

Qué viaje, ¿eh?

Estos son solo dos de los nuevos métodos en el mundo emergente de la criptografía post-cuántica. No todos los métodos que se están proponiendo están basados en retículos, sin embargo. Hay mucha información para asimilar por ahí, y probablemente mucha investigación increíble para leer (¡que todavía necesito revisar!).

Aún así, la criptografía basada en retículos parece prometedora como la próxima generación de algoritmos criptográficos estándar.

Además, parte del atractivo de usar retículos está relacionado con sus características, algo de lo que aún no hemos hablado. Debido a que todo está basado en anillos detrás de escena, y dado que los anillos soportan dos operaciones, esto es terreno fértil para algo súper genial: el cifrado completamente homomórfico, o FHE para abreviar. Este será el tema para el próximo (y probablemente el último) artículo de esta serie.

¡Hasta la próxima!