Criptografía 101: Aprendizaje con Errores en Anillos

Este artículo forma parte de una serie más larga sobre criptografía. Si este es el primer artículo con el que te encuentras, te recomiendo comenzar desde el principio de la serie.

En nuestra entrega anterior, introdujimos otra estructura para jugar: los anillos. Estos abrirán el camino para una criptografía fundamentalmente diferente a todo lo que hemos visto hasta ahora.

Pero no nos adelantemos — hay una cosa más que necesitamos hacer antes de intentar entender cualquier técnica criptográfica nueva.

Ningún método es utilizable en la práctica a menos que sea seguro, por así decirlo. A estas alturas de la serie, sabemos perfectamente que la seguridad se mide en términos de cuán difícil es romper un esquema.

Para responder a esto, necesitamos entender el problema matemático asociado que se supone que es difícil. Hemos visto algunos hasta ahora en la serie — como el problema de factorización de enteros y el problema del logaritmo discreto.

Por supuesto, hay más problemas de este tipo. Hoy, aprenderemos sobre uno completamente nuevo, que será la columna vertebral de la criptografía basada en anillos.

Bien, ¡veamos con qué estamos trabajando!

Preparando el Terreno

El Aprendizaje con Errores en Anillos (RLWE por sus siglas en inglés) es un problema basado en polinomios. Un anillo cociente de polinomios, para ser precisos. Como breve recordatorio, esto significa que estaremos trabajando con algún anillo:

$$\mathbb{F}_q[X]/(f(X))$$

De tal manera que podemos reducir cualquier polinomio módulo $f(X)$ — el polinomio módulo.

Explicamos esto en detalle en el artículo anterior, ¡así que revísalo si es necesario!

Ahora... ¿Qué podemos hacer con esto?

Desarrollemos nuestra comprensión paso a paso. Dados un par de polinomios $A(X)$ y $S(X)$, podemos calcular su producto, así:

$$B(X) = S(X).A(X)$$

Las propiedades del anillo entran en juego en este punto: $B(X)$ se reduce módulo algún polinomio $f(X)$ de elección, asegurando que el grado siempre esté acotado.

Aquí hay una pregunta para ti: si te doy $B(X)$ y $A(X)$, ¿qué tan difícil crees que sería recuperar $S(X)$?

Bueno, ¡no es tan difícil en absoluto!

Resulta que, con una elección cuidadosa de $f(X)$, cada polinomio en el anillo puede ser invertido. Funciona exactamente como los inversos modulares en campos finitos: para cada polinomio $P(X)$, podemos encontrar algún $P^{-1}(X)$ tal que:

$$P(X).P^{-1}(X) \ \textrm{mod} \ f(X) = 1$$

Tener esta herramienta hace que la tarea sea realmente simple: simplemente encuentras $A^{-1}(X)$ y calculas:

$$S(X) = B(X).A^{-1}(X)$$

Bien, esto no parece un buen candidato para un problema difícil. ¿O sí? ¿Qué tal si lo modificamos un poco?

Cambiando el Enfoque

Con solo un pequeño empujón en la dirección correcta, podemos transformar esta expresión aparentemente inocente y fácil de resolver en algo mucho más útil. Es realmente bastante simple — todo lo que necesitamos hacer es añadir algún error o polinomio de ruido a la mezcla:

$$B(X) = S(X).A(X) + E(X)$$

El error necesita ser pequeño — solo un poco de ruido es suficiente, como veremos más adelante.

¡Eso es todo! Bastante sorprendente el giro de la trama, dado las cosas locas a las que estamos acostumbrados.

Este ajuste bastante discreto esconde mucha complejidad. Reflexionemos sobre esta expresión por un momento.

Reorganizando la expresión un poco, obtenemos:

$$E(X) = B(X) - A(X).S(X)$$

Viéndolo desde esta perspectiva, es fácil ver que dados cualesquiera polinomios $A(X)$ y $B(X)$, básicamente podemos elegir cualquier $S(X)$ y calcular $E(X)$. Lo que esto significa es que no hay una forma única o directa de relacionar $A(X)$ y $B(X)$. La solución ya no es directa.

¡Suena prometedor!

Pero antes de seguir con un ejemplo, hay algo de lo que necesitamos hablar. ¿Qué es el aprendizaje en "aprendizaje con errores"?

El Problema del Aprendizaje

Para esta sección, vamos a necesitar cambiar de perspectiva nuevamente. No te preocupes — nada extraño. Las cosas serán bastante amigables esta vez.

En lugar de los propios polinomios $A(X)$ y $B(X)$, trabajemos con sus evaluaciones. Entonces, elegiremos algunos valores para $X$ y calcularemos:

$$a = (A(x_0), A(x_1), A(x_2), ..., A(x_{n-1})) \in {\mathbb{F}_q}^n$$ $$b = (B(x_0), B(x_1), B(x_2), ..., B(x_{n-1})) \in {\mathbb{F}_q}^n$$

Estos vectores están claramente relacionados — siguen la ecuación polinómica que describimos antes:

$$b = a \cdot s + e \ \textrm{mod} \ q$$

Donde $a \cdot s$ es la multiplicación componente a componente.

Como siempre, la pregunta es, ¿por qué esto sería útil? ¡La respuesta se volverá más clara a medida que exploremos algunas aplicaciones! Aguanta un momento conmigo.

El problema ahora se enuncia de la siguiente manera:

Dados $a$ y $b$, encuentra $s$.

En la misma línea que la discusión anterior, esto es realmente difícil siempre que $e$ sea cuidadosamente elegido — es decir, que sea muestreado al azar de una distribución específica. Imagina algo similar a una distribución normal.

Lo que hace que esto sea difícil es que, debido a la adición del vector de ruido $e$, es realmente complicado decir si $b$ es solo un vector aleatorio o si fue realmente calculado como $b = a \cdot s + e \ \textrm{mod} \ q$. A la inversa, es realmente difícil determinar $s$ con conocimiento de $a$ y $b$. Siempre y cuando $s$ y $e$ no sean revelados, por supuesto.

Estas dos versiones de la misma moneda se conocen como el problema de decisión y el problema de búsqueda. La mayoría de los problemas en criptografía pueden escribirse en cualquiera de las versiones — son equivalentes.

Ok, genial. ¿Y ahora qué? Tener un problema difícil no es divertido a menos que podamos construir algo con estos nuevos juguetes.

Construyendo un Ejemplo

Construiremos algo basado en este artículo, que es uno de los trabajos fundamentales en esta área.

Imaginemos que queremos cifrar un mensaje. Típicamente, abordaríamos esto generando claves y usándolas para aplicar alguna operación en el mensaje que luego pueda ser deshecha por el receptor. Y eso es exactamente lo que haremos.

Encriptación

Nuestra clave será simplemente un polinomio muestreado aleatoriamente $s(X)$. Para simplificar, simplemente escribiremos $s$. Luego, necesitamos un mensaje para cifrar. Para nuestros propósitos, este será otro polinomio, que se denotará como $m$. Sus coeficientes están acotados entre $0$ y algún entero $t$, menor que $q$.

Por ejemplo, $t$ puede ser $2$ para que los coeficientes sean realmente una secuencia binaria.

La encriptación es realmente simple: solo muestreamos un par de polinomios $a$ y $e$, y calculamos:

$$c_0 = a.s + t.e + m \ \textrm{mod} \ q$$ $$c_1 = -a$$

El par $(c_0, c_1)$ constituye el texto cifrado. Estos pueden enviarse a un receptor, que ahora intentará recuperar el mensaje con conocimiento de $s$. Debido a esto, es un algoritmo de cifrado simétrico.

Desencriptación

Al recibir el mensaje, el receptor simplemente calculará:

$$m = c_0 + c_1.s \ \textrm{mod} \ t$$

¡Sí! Es así de simple.

Aquí, hagamos las matemáticas y verifiquemos que esto funciona. Sustituyendo $c_0$ y $c_1$ nos queda:

$$(c_0 + c_1.s) \ \textrm{mod} \ t = (t.e + m) \ \textrm{mod} \ t = m$$

Como puedes ver, el error mágicamente desaparece porque las operaciones se realizan módulo $t$. ¡Maravilloso!

Si comparamos estas dos expresiones:

$$m = c_0 + s.c_1$$ $$B(X) = E(X) + S(X).A(X)$$

Probablemente puedas ver el paralelismo entre esto y nuestra primera formulación del problema. Cualquiera que vea el texto cifrado sin conocimiento de $s$ no podría distinguir $c_0$ y $c_1$ de polinomios aleatorios.

Esencialmente, tendrían que resolver el problema RLWE. Y ya sabemos — ¡es condenadamente difícil de hacer!

Aquí hay un enlace a un ejemplo aún más simple de cifrado, donde codificamos un solo bit. El ejemplo se basa en algunas cosas que discutiremos más adelante — pero si deseas algo más interactivo o necesitas un descanso de la lectura, ¡puedes ir a verlo!

Habrá tiempo para que exploremos más métodos más adelante. Por ahora, es importante poner eso en espera y en su lugar explorar una conexión muy interesante.

Retículos

Woah woah woah. ¿Qué?

Estábamos hablando de polinomios, ¿y ahora me hablas de retículos? ¿Qué es siquiera un retículo?

De acuerdo, tienes razón, necesitamos un poco de contexto. Aunque todavía no hemos definido qué es un retículo — ni su conexión con los anillos — lo que puedo decir es que muchos métodos PQC se basan en problemas sobre retículos. Y por eso es importante entender qué son. Estudiar su conexión con RLWE también podría proporcionarnos alguna idea para evaluar su seguridad.

Con eso, estamos listos para algunas definiciones.

¿Qué es un Retículo?

Toma un punto en el espacio bidimensional. Ahora, dibuja dos vectores así:

Click to zoom

Por supuesto, para ser utilizables en criptografía, estos vectores necesitan tener valores enteros.

Con esto, comenzamos un proceso iterativo.

Coloca un punto al final de cada vector. Usándolos como puntos de partida, repite el proceso. Ah, y también haz lo mismo en la dirección opuesta de los vectores originales.

Lo que obtienes es un conjunto infinito de puntos que están uniformemente espaciados, como si crearan un patrón infinito. Este es un retículo generado por nuestros dos vectores base.

Click to zoom

Por cierto, cuando trabajamos con campos finitos, estos retículos no son infinitos — se reducen módulo $q$, como esperarías.

Muy bien, muy bien. ¡Otro juguete más! Pero sabemos que esto no es bueno para la criptografía a menos que podamos proponer un problema difícil alrededor de él.

El Problema del Retículo

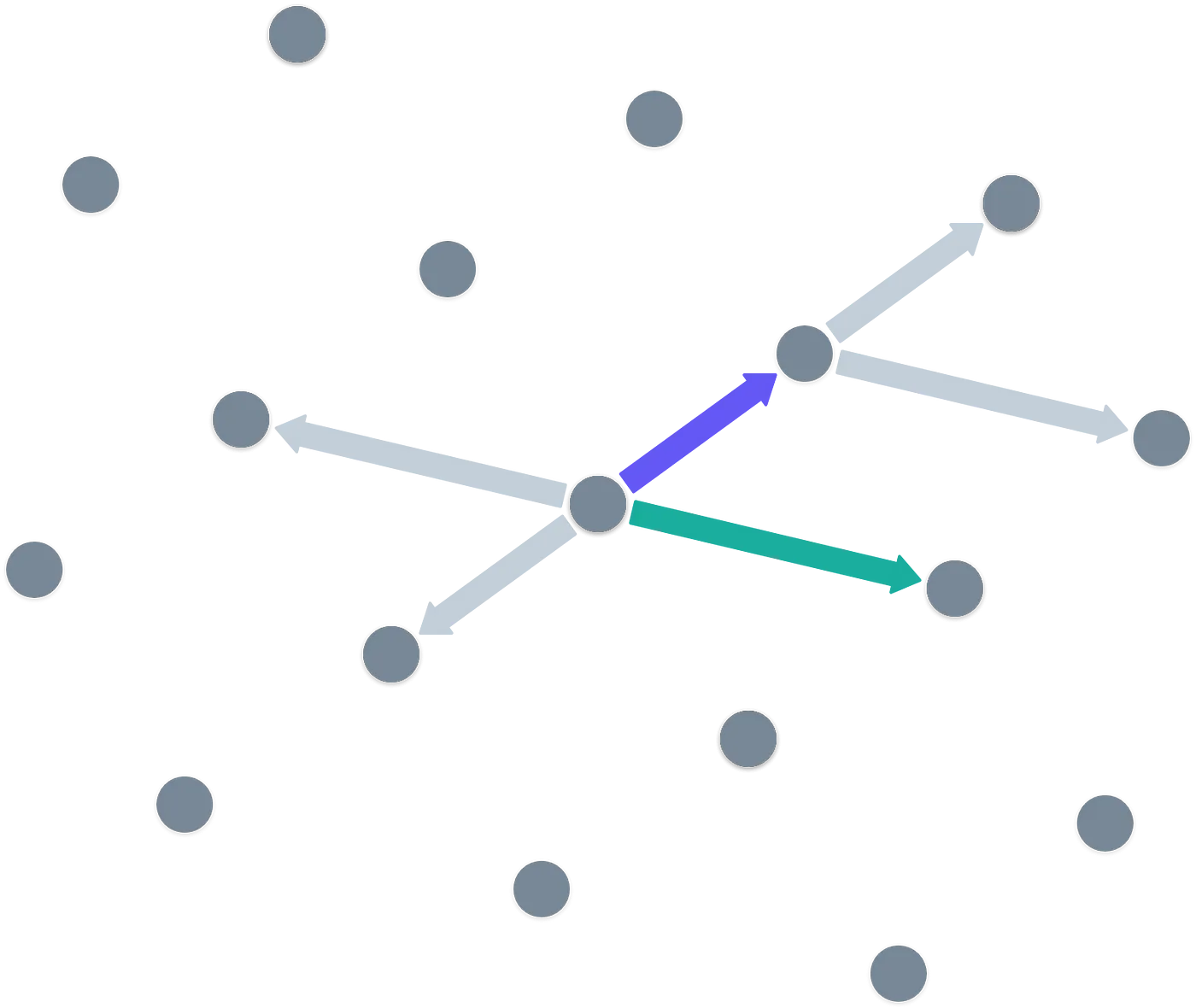
Con los vectores en la imagen de arriba, es bastante fácil detectar un patrón en el retículo. Imagina que te doy algún punto aleatorio que no está en el retículo — como el patrón es simple, es bastante fácil decir qué punto del retículo es el más cercano al que te di:

Click to zoom

Una pregunta para ti: ¿es siempre tan fácil?

Pausa para pensar.

.

.

.

.

.

.

. ☕️ Un café siempre ayuda.

.

.

.

.

.

.

¡Bien, eso es más que suficiente!

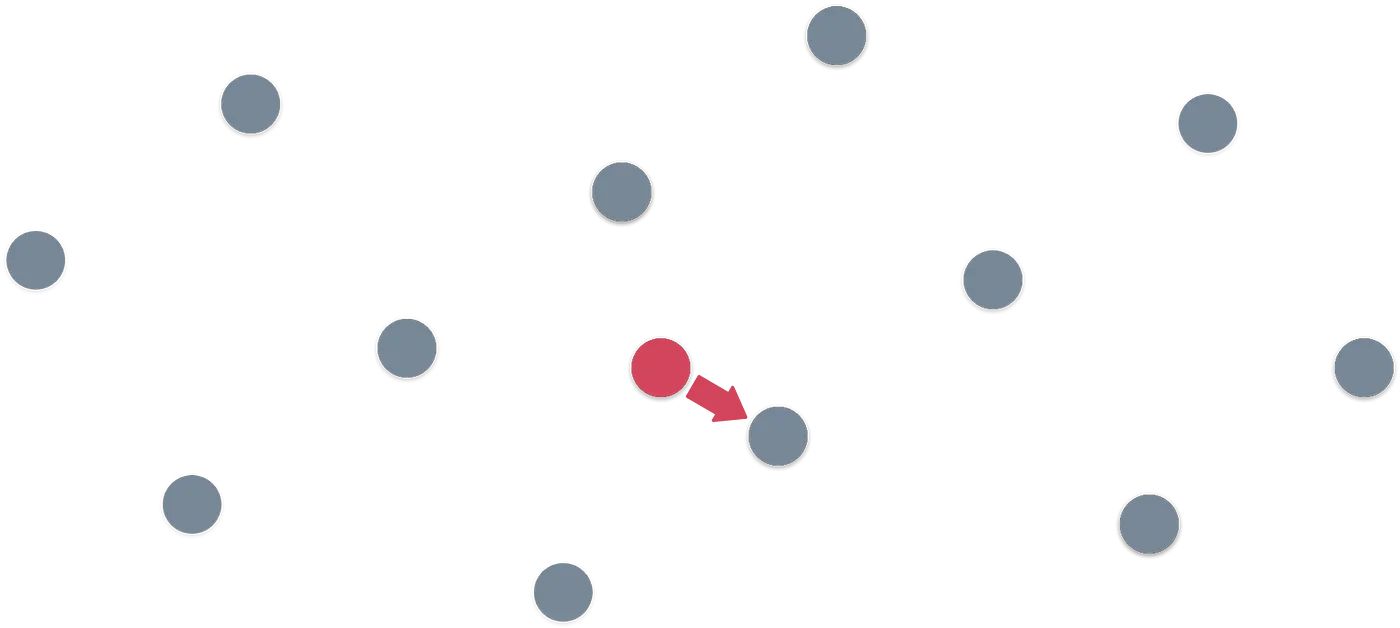
La respuesta es que depende. Depende de los vectores base que elijamos, y en algunos casos, el patrón emergente no será tan simple. Como en el siguiente ejemplo:

Click to zoom

El patrón infinito no es tan simple de detectar ahora. Y la forma de encontrar cuál es el punto del retículo más cercano al punto rojo es comenzar a probar combinaciones de los vectores base hasta que obtengamos un buen candidato. Pero... ¿Cómo podemos estar seguros de que nuestro candidato es el punto más cercano en el retículo?

Este problema se llama Problema del Vector Más Corto, o SVP por sus siglas en inglés. Y es condenadamente difícil. En general, la dificultad aumenta debido a dos cosas:

• Cuán colineales son los vectores base — o cuán cerca están de ser paralelos.
• El número de dimensiones en las que definimos el retículo.

Oh, sí, porque no estamos limitados a dos dimensiones. ¿Se me olvidó mencionar eso? No es raro usar retículos en cientos o incluso miles de dimensiones.

Click to zoom

¡Podemos usar tantas como necesitemos! Y eso hace que el problema sea realmente, realmente difícil.

Espera, detente. Un momento. ¿No estábamos buscando una conexión con RLWE? No queremos alejarnos demasiado de nuestro objetivo principal. ¿Cómo está todo esto conectado, entonces?

RLWE y Retículos

Comenzamos trabajando con polinomios, y ahora estamos lidiando con vectores. Estas construcciones parecen operar en mundos completamente diferentes — pero en realidad, no están tan alejados. Mira esto:

$$P(X) = p_0 + p_1X + p_2X^2 + ... + p_{n-1}X^{n-1}$$ $$p = (p_0,p_1, p_2, ..., p_{n-1})$$

¿Ves lo que hicimos? ¡Acabamos de escribir los coeficientes del polinomio como un vector! Encontrarás que sumar estos vectores es equivalente a sumar los polinomios asociados.

Con esta nueva visión, examinemos nuestro problema difícil original en RLWE, nuevamente:

$$E(X) = B(X) - A(X).S(X)$$

Imagina que $B(X)$ es un vector, representando un punto en el espacio n-dimensional. Necesitamos encontrar $S(X)$ tal que $A(X).S(X)$ esté lo más cerca posible de $B(X)$. En consecuencia, $E(X)$ será la diferencia más pequeña posible entre estos polinomios — y aplicando nuestra equivalencia anterior, es el vector más corto.

¡Ajá! ¡Esto se está perfilando bien! Al pensar en el polinomio de ruido como un vector corto, al menos el objetivo final de ambos problemas parece intercambiable!

Sin embargo, parece haber un problema: ¿cómo se relaciona la expresión $A(X).S(X)$ con la búsqueda de puntos en un retículo? Si podemos atar este cabo suelto, entonces obtendremos la conexión completa entre estos problemas.

Este no es tan directo. Es el tramo final — por favor, aguanta conmigo un poco más!

¿Recuerdas los ideales de anillo? ¿Esas cosas molestas que eran súper abstractas de definir? ¡Los necesitaremos aquí!

El polinomio $A(X)$ se utiliza para definir un ideal en nuestro anillo polinómico de elección. Se define como:

$$I = \{A(X).S(X) \ \textrm{mod} \ f(X) \ / \ S(X) \in \mathbb{F}_q[X]/(f(X)) \}$$

Este es un ideal bilateral, ya que la conmutatividad se cumple en anillos polinómicos.

Ya sabemos cómo se puede usar un ideal para calcular un anillo cociente. Todo lo que queda es mapear cada polinomio en el ideal a un vector — y justo ahí, amigos míos, ¡acabamos de encontrar nuestro retículo!

Estos a menudo se llaman retículos ideales, debido a cómo se originan de un ideal del anillo polinómico.

Curiosamente, los vectores base para este retículo pueden calcularse tomando $A(X)$ y multiplicándolo por $X$ sucesivamente. Y en algunos casos especiales (como cuando se usan polinomios ciclotómicos), la base termina siendo una rotación de los coeficientes de $A(X)$.

Por ejemplo, usando el polinomio $A(X) = a_0 + a_1X + a_2X^2$, y trabajando con el anillo $\mathbb{F}[X]/(X^3 + 1)$, la base para el retículo ideal está formada por los vectores $(a_0, a_1, a_2)$, $(a_2, a_0, a_1)$ y $(a_1, a_2, a_0)$.

Resumen

Creo que eso es más que suficiente para tener una comprensión inicial de las estructuras que sustentan la mayoría de los métodos post-cuánticos.

¡Hay mucho más sobre RLWE y retículos por ahí, por supuesto! Pero tendremos que contentarnos con esto, al menos por ahora.

La mayoría de las veces, el objetivo de esta serie no es entrar en detalles rigurosos sobre cada estructura o construcción que presentamos — lo que considero más importante aquí son los conceptos e ideas generales que discutimos.

Nuestra principal conclusión de este artículo debería ser los problemas RLWE y SVP, y también los conceptos generales de cómo funcionan los anillos y los retículos en la práctica.

Eso será todo lo que necesitamos para explorar algunos métodos PQC — ¡ahora estamos listos para llegar a lo bueno!

Presentar algunos de estos métodos será el tema del próximo artículo. ¡Hasta pronto!