Curvas Elípticas En Profundidad (Parte 2)

La última vez, definimos qué son las curvas elípticas, y diseñamos una forma (sospechosamente complicada) de sumar puntos en la curva. Y dimos pistas sobre cómo esta operación era clave para aplicaciones criptográficas.

Sin embargo, las curvas en sí mismas — definidas sobre los números reales — no son las construcciones que buscamos.

La criptografía es una disciplina de precisión discreta. Queremos algoritmos que produzcan resultados consistentes y reproducibles. En otras palabras, buscamos el determinismo, que a grandes rasgos significa que usar las mismas entradas debería producir las mismas salidas, sin importar qué.

Trabajar con números reales es bastante engorroso en este sentido, porque normalmente usamos aritmética de punto flotante, y en consecuencia, los errores de redondeo están siempre presentes, haciendo las operaciones imprecisas.

Debido a los errores de redondeo, el resultado de sumar $P \oplus Q$ podría incluso no caer exactamente en la curva (cuando trabajamos sobre los números reales).

Esto requiere una estrategia diferente.

¡Ese será nuestro punto de partida para hoy! Comenzaremos con un pequeño desvío, y luego volveremos directamente a las curvas elípticas.

Un Dominio Adecuado

A diferencia de los números reales, los enteros son muy precisos para operar. Como no hay decimales de qué preocuparse, ¡los errores de redondeo parecen estar fuera del menú!

Si bien esto es cierto para la suma, resta y multiplicación, parece que la división podría ser un poco problemática: $1$ dividido por $3$ claramente no produce un entero, y estamos de vuelta en el reino de la aritmética de punto flotante.

También vale la pena preguntarnos qué tan grandes podemos permitir que sean nuestros enteros. Después de todo, necesitamos representarlos de alguna manera — y permitir que crezcan demasiado es problemático cuando intentamos almacenarlos y manejarlos en una computadora.

Así que sí, enteros — y más específicamente, enteros positivos — , pero estamos a mitad de camino. Necesitamos una manera de mantener nuestros valores bajo control (acotados), mientras también averiguamos cómo manejar la división.

Aritmética Modular

Para remediar esto, utilizaremos una herramienta simple: la operación módulo, y la aritmética modular.

He hablado de esto en artículos anteriores, así que asumiré familiaridad con estos conceptos.

Al usar la operación módulo para acotar los resultados de nuestras operaciones de suma, resta y multiplicación, esencialmente limitamos los posibles enteros con los que podemos trabajar a un conjunto finito, como este:

$$\mathbb{F}_{11} = \{0,1,2,3,4,5,6,7,8,9,10\}$$

Estamos usando el símbolo $\mathbb{F}$ aquí, porque el conjunto resultante será un campo (de ahí el $\mathbb{F}$). Un campo es simplemente un conjunto donde la suma, resta, multiplicación y división están bien definidas.

Primer problema, resuelto (acotamiento). Como nuestro campo es ahora un conjunto finito, simplemente lo llamamos un campo finito.

La división requerirá algo más de trabajo — junto con una observación inteligente.

Una Perspectiva Diferente

Tomemos por ejemplo $5 \ \textrm{mod} \ 3$. Obviamente el resultado es $2$. ¿Cómo llegamos ahí?

Podemos describir el proceso más rigurosamente como encontrar una solución a esta ecuación:

$$5 = 3k + x$$

Y requiriendo que $x$ sea un valor entre $0$ y $4$ (un elemento de $\mathbb{F}_5$). Esto resulta en $k = 1$ y $x = 2$.

Sin embargo, está claro que existen otras soluciones. Por ejemplo, $k = 2$ y $x = -1$. Como probablemente puedas notar a estas alturas, podemos encontrar infinitas soluciones enteras para esta ecuación.

De hecho, el conjunto de todos los posibles valores para $x$ forma una clase de equivalencia.

Sí, está bien, pero... ¿Por qué debería importarnos? Resulta que al mirarlo de esta manera, ¡hay algo que podemos hacer con la división!

Si lo pensamos un poco, el resultado de alguna división $1 / a$ no es más que otro número, que satisface una propiedad particular. Por ejemplo, el resultado de $1 / 2$ es $0.5$, y para $1 / 3$, obtenemos $0.333(...)$. Todos estos resultados comparten esta propiedad:

$$a.\left ( \frac{1}{a} \right) = 1$$

Entonces, en lugar de pensar en términos de división, pensemos en términos de encontrar un número recíproco. Nos preguntamos:

Dado algún número en nuestro campo, ¿podemos encontrar otro número (también en el campo), de modo que cuando los multiplicamos juntos, el resultado es $1$?

En otras palabras, estamos buscando una solución a esta ecuación:

$$a.x \ \textrm{mod} \ p = 1$$

Que — probablemente lo hayas adivinado — puede traducirse a esta forma:

$$a.x - p.k = 1$$

¡Y estamos de vuelta en el escenario de antes! Si resulta que podemos encontrar un valor válido para $x$, decimos que es el inverso modular de $a$, y lo escribimos como $a^{-1}$.

Esta forma se conoce como identidad de Bézout, y por supuesto, solo nos interesan las soluciones enteras para $x$ y $k$ (es una ecuación diofántica lineal).

Es importante destacar que una solución podría no existir. Excluyendo el cero, la condición para que exista el inverso modular de un entero $a$ es que sea coprimo con el tamaño del campo $p$, lo que significa que no comparten factores — o que su máximo común divisor (MCD) es $1$.

Podemos probarlo muy rápidamente. Supongamos que $a$ y $p$ comparten algún factor $t$, lo que significa que $a = t.a'$ y $p = t.p'$. Entonces, podríamos factorizar $t$, y la ecuación anterior se convertiría en:

$$t(a'.x - k.p') = 1$$

Sin importar qué valores de $x$ y $k$ usemos, el lado izquierdo nunca será $1$, lo que significa que la ecuación no tendría solución. En consecuencia, si $a$ y $p$ comparten un factor, entonces el inverso modular no existe.

Hay una solución muy simple para esto: ¡elegir un número primo para $p$! Por definición, cualquier número primo tiene solo dos factores: $1$ y sí mismo — lo que significa que, siempre que el campo finito tenga un tamaño primo, todos sus elementos (excluyendo el cero) tendrán un inverso modular.

Bueno, de hecho, por definición, el inverso de $0$ es $0$.

¡Maravilloso! Esto significa que algo similar a la división está definido para cada elemento en el conjunto — por lo que es efectivamente un campo.

De Vuelta a las Curvas Elípticas

Las operaciones entre elementos de un campo finito producen resultados determinísticos y bien definidos, ¡que es exactamente lo que queríamos!

Ahora todo lo que necesitamos es definir nuestras curvas elípticas sobre estos conjuntos, en lugar de sobre los números reales. No hay nada demasiado elaborado aquí — ya hemos derivado fórmulas explícitas para la suma de puntos y la duplicación en nuestro encuentro anterior. El único ajuste que debemos hacer es reemplazar la división por la multiplicación por inversos modulares.

Por ejemplo, la duplicación de puntos se realiza simplemente ejecutando estos cálculos a continuación:

$$\\ m = (3x_P + a)(2y_P)^{-1} \\ n = y_P - mx_P$$ $$\\ x_R = m^2 - 2x_P \\ y_R = -(mx_R + n)$$

Así que sí, nada elaborado — excepto que todos esos resultados se reducen módulo $p$. También sabemos que son elementos en nuestro campo finito — lo que significa que el $R$ resultante también tendrá coordenadas enteras.

Hay una sutileza que debemos notar aquí. Cuando analizamos el caso en los números reales, teníamos garantizado encontrar un tercer punto de intersección. No es inmediatamente obvio que esto se traduzca a un escenario de campo finito. Afortunadamente para nosotros, ¡las operaciones de suma y duplicación también se comportan bastante bien en campos finitos!

Debido a esto, las curvas elípticas no se verán como "curvas" en sí cuando se definen sobre campos finitos. En cambio, se verán más como un conjunto de puntos limitados a un cuadrado de lado $p$, como este:

Click to zoom

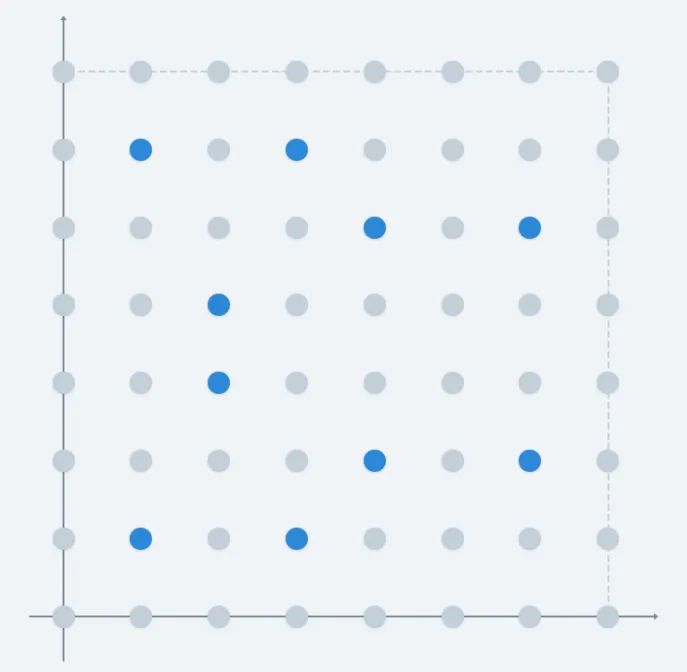
Puedes experimentar con diferentes curvas aquí.

Y por supuesto, ¡nos falta contar el punto en el infinito!

No es evidente solo mirando esta imagen cuál es el resultado de sumar dos puntos cualquiera en la curva. Aún así, las reglas de la cuerda y la tangente están definidas por las ecuaciones que ya derivamos, independientemente del hecho de que estamos trabajando con un conjunto diferente. Es solo que las visualizaciones no ayudan mucho ahora:

Click to zoom

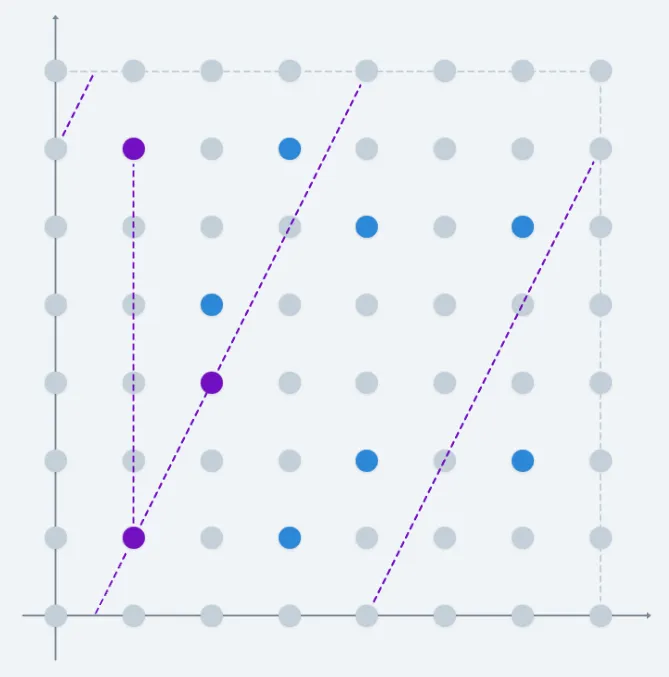
Como puedes ver, las líneas se cortan cuando alcanzan los límites de nuestro dominio cuadrado — y esto tiene sentido, porque las líneas también están definidas módulo $p$.

¡Todo está definido módulo $p$ ahora!

Una forma más natural de pensar en esto es notando que los bordes izquierdo y derecho son equivalentes bajo módulo $7$ ($7 \ \textrm{mod} \ 7 = 0$), así que si pudiéramos doblar nuestro cuadrado en tres dimensiones, podríamos pegar esos bordes juntos, obteniendo una superficie cilíndrica 3D. Exploremos esto, solo por diversión.

Lo mismo puede hacerse con los bordes superior e inferior. Requiere un poco de imaginación, pero es como si nuestra curva elíptica estuviera realmente definida sobre un dominio con forma de dona — un toride. ¡En ese espacio, las líneas serían efectivamente continuas!

Click to zoom

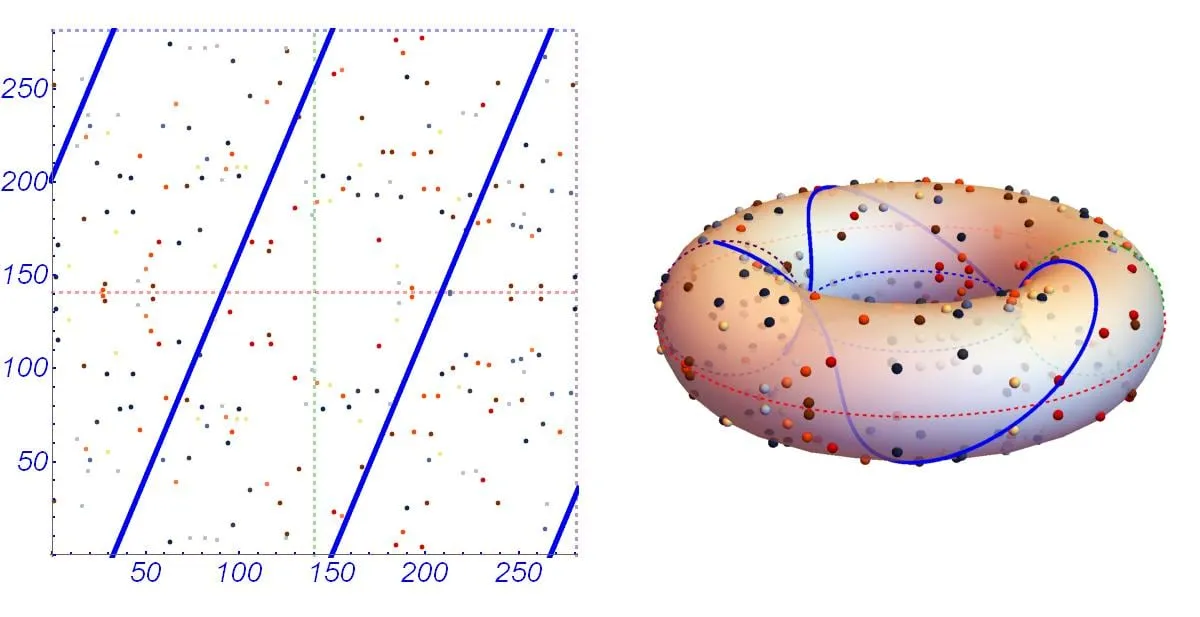
Para aquellos que han estudiado topología, ¡esto les recordará mucho a las topologías cociente!

No necesitamos preocuparnos por estas transformaciones, pero siempre es un buen ejercicio tratar de llevar nuestra comprensión un poco más allá, ya que puede ayudar a obtener nuevas perspectivas.

Hablando de eso — hay un punto particularmente problemático que no hemos tratado con mucha elegancia hasta ahora: el punto en el infinito. Se siente un poco forzado — parece que no podemos ubicarlo en ninguna parte. Y después de nuestro pequeño ejercicio con doblado y rosquillas, veamos si podemos encontrar una manera de ubicarlo en algún lugar.

Coordenadas Proyectivas

Como nuestra curva está definida sobre $\mathbb{R}^2$ o ${\mathbb{F}_p}^2$, no es descabellado que hayamos imaginado las curvas elípticas como puntos en un plano (o un plano deformado, en los casos que examinamos hace apenas unos momentos).

Esto se llama espacio afín (junto con el punto en el infinito), a veces denotado $\mathbb{A}^2$.

Aquí hay una pregunta bastante inusual: ¿dónde podemos situar ese plano? Es decir, un plano es solo un plano — un lienzo abstracto para que representemos cosas en él. ¿Tiene sentido siquiera tratar de situarlo en algún lugar?

De hecho, ¡sí! Y el primer paso para hacerlo es moverse una dimensión arriba.

En tres dimensiones, un plano está realmente definido por una ecuación lineal:

$$p: ax + by + cz + d = 0$$

Hay infinitos planos diferentes que podríamos representar en tres dimensiones. Ahora "situar" un plano en algún lugar sí tiene sentido; todo lo que necesitamos es elegir uno de los infinitos planos que están disponibles para nosotros en el espacio 3D.

Y realmente no necesitamos nada elaborado. Podemos simplemente elegir el plano horizontal ($x-y$) que se sitúa en $z = 1$. Imaginemos que dibujamos nuestra curva elíptica en este plano.

Aquí es donde se pone interesante: para cada punto $P=(x,y)$ en la curva, si trazamos una línea que pasa por el origen $(0,0,0)$ y $(x,y,1)$, esa línea intersectará el plano $z = 1$ en exactamente un punto: $P$. ¡Así que estas líneas son equivalentes a los puntos mismos!

Click to zoom

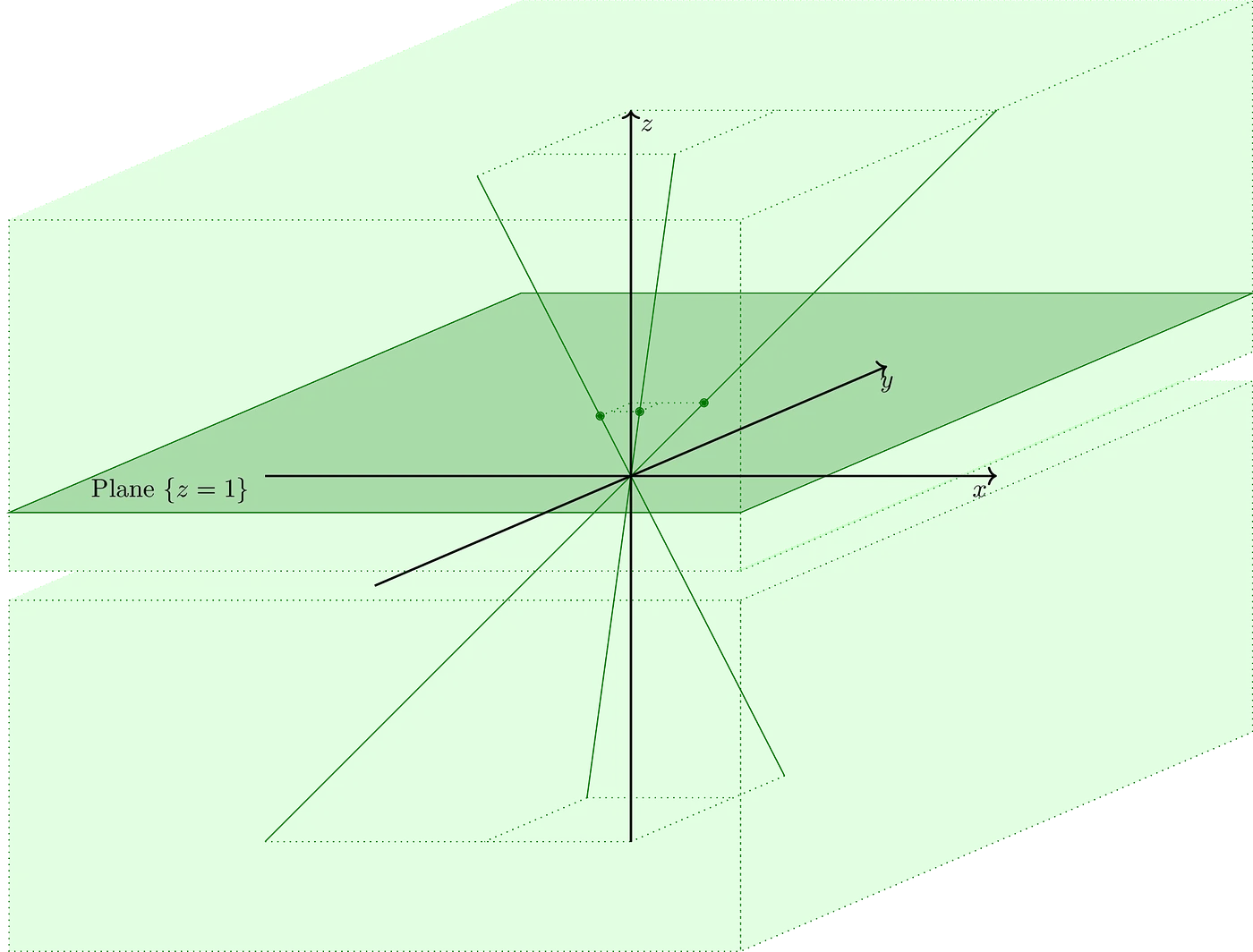
Esto se llama espacio proyectivo, y se denota por $\mathbb{P}^2$. Para hacer las cosas un poco más claras, denotemos los puntos en este espacio 3D como $(X,Y,Z)$.

Ahora, cualquier punto en cualquiera de estas líneas preserva la relación $X:Y:Z$. Es decir, si examinamos la línea definida por $P=(x,y,1)$, entonces el punto $(2x,2y,2)$ estará en la misma línea, y también lo estará $(3x, 3y, 3)$, o en general, cualquier punto de la forma $(tx, ty, t)$. Esto se suele representar mediante la notación $(X:Y:Z)$ para reflejar esta noción de relaciones.

Como elegimos $z = 1$, podemos recuperar los valores originales de $x$ e $y$ mediante:

$$x = X / Z, y = Y / Z$$

Y estas expresiones pueden sustituirse en nuestra ecuación de curva elíptica, produciendo esta expresión:

$$e: \frac{Y^2}{Z^2} = \frac{X^3}{Z^3} + a\frac{X}{Z} + b$$

Que, después de eliminar los denominadores, da:

$$e: Y^2Z = X^3 + aXZ^2 + bZ^3$$

Tomemos un respiro por un segundo. Debo admitir: esto parece ser una complicación innecesaria.

Pero a veces, estas complicaciones aparentemente innecesarias pueden revelar nuevas perspectivas que pueden hacer nuestras vidas mucho más fáciles.

Aquí hay un gran video que ilustra perfectamente esta idea. No tiene mucho que ver con curvas elípticas, ¡pero creo que es simplemente asombroso!

Al examinar más de cerca, efectivamente ha ocurrido algo fantástico.

Verás, cada punto en la curva que vive en el plano $z = 1$ tiene la forma $(X,Y,1)$. Sin embargo, un "punto en la curva" es realmente cualquier punto que satisface la ecuación $e$. No hay una razón real para restringirnos a un plano aquí.

Sin embargo, estamos trabajando con estas coordenadas proyectivas — donde cada línea que comienza en el origen es una clase de equivalencia. Y en este contexto, resulta que hay otro punto que satisface la ecuación: el punto $(0,1,0)$. Puedes comprobarlo tú mismo — ¡simplemente funciona!

Esta línea es completamente paralela al plano $z = 1$ — así que nunca lo intersecta. Satisface la ecuación, pero no tiene punto representativo en nuestro espacio afín (el plano).

¿Te suena familiar?

Adivina qué — ¡este es el punto en el infinito que estamos buscando! Pero ahora podemos representarlo realmente. Sin embargo, demostrar este hecho requiere un poco de esfuerzo. En aras de no complicar demasiado las cosas, evitaremos seguir ese camino.

Utilidad

Las coordenadas proyectivas ofrecen esta nueva visibilidad sobre el punto en el infinito. Naturalmente, podemos preguntarnos si eso es todo para lo que son buenas, o si es solo un artefacto extremadamente rebuscado para obtener algo de comprensión adicional.

¡Resulta que las coordenadas proyectivas son bastante útiles! Cuando trabajamos las fórmulas para la suma y multiplicación de puntos, sucede algo interesante: ¡somos capaces de evitar algunos inversos modulares!

Los inversos modulares son bastante costosos de calcular. El algoritmo estándar para calcularlos es el algoritmo extendido de Euclides.

No lo cubriremos aquí por brevedad, pero puedes ver cómo funciona aquí.

Lo que es seguro es que requiere considerablemente más esfuerzo que simples multiplicaciones. ¡Y así, usar coordenadas proyectivas conduce a operaciones de curva elíptica más rápidas!

En criptografía, donde necesitamos realizar miles o millones de estas operaciones, cada pequeña mejora cuenta.

Resumen

¡Hemos cubierto bastante terreno hoy! Pasamos de los números reales a los campos finitos, vimos cómo nuestras curvas se transforman en este nuevo escenario, e incluso encontramos una manera de representar adecuadamente nuestro punto en el infinito.

Por supuesto, esto está lejos de ser el final de la historia.

Todavía tenemos que hablar sobre lo que hace que las curvas elípticas sean útiles en criptografía. Pero ahora que estamos trabajando en este escenario acotado, sucede algo notable: las curvas elípticas se comportan como grupos. Esto es lo que les da sus superpoderes criptográficos.

La próxima vez, exploraremos esta estructura de grupo, veremos por qué es útil, y finalmente llegaremos al corazón de por qué las curvas elípticas son una herramienta tan fundamental en la criptografía moderna.

¡Hasta entonces!