Criptografia 101: Protocolos à Vontade

Este é parte de uma série de artigos sobre criptografia. Se este é o primeiro artigo que você encontra, eu recomendo começar do início da série.

Beleza! Já chegamos longe. Temos grupos (e em particular curvas elípticas) e hashing como ferramentas à nossa disposição, e já vimos eles em ação.

Mas muito mais pode ser feito com o que sabemos. Este artigo será dedicado a listar e explicar protocolos criptográficos baseados em curvas elípticas.

Devo apontar que os mesmos protocolos podem ser construídos usando o grupo de inteiros módulo $q$. Vamos ficar com curvas elípticas, já que existem alguns benefícios em usá-las. Essa discussão acontecerá em outro momento.

Esta lista de forma alguma é completa — tem mais por aí. Ainda assim, isso deve fornecer uma base sólida para você ter uma boa compreensão do que é possível com o que sabemos até agora.

Aperte o cinto, e vamos mergulhar nisso!

Troca de Chaves

Lembra do exemplo de encriptação simétrica? Ele dependia do uso de uma chave secreta compartilhada. Mencionamos brevemente que compartilhar uma chave secreta por um canal inseguro não é uma boa ideia — qualquer um poderia estar escutando. E se estiverem, e conseguirem a chave secreta compartilhada, então poderiam decriptar qualquer mensagem subsequente!

Felizmente, existem mecanismos para gerar chaves compartilhadas de forma segura. A técnica mais comum para fazer isso é o algoritmo de troca de chaves Diffie-Hellman. Este método foi originalmente formulado usando os inteiros módulo $q$, mas pode facilmente ser estendido para curvas elípticas — e obtemos o chamado método Elliptic Curve Diffie-Hellman (ECDH). É assim que ele se parece:

Click to zoom

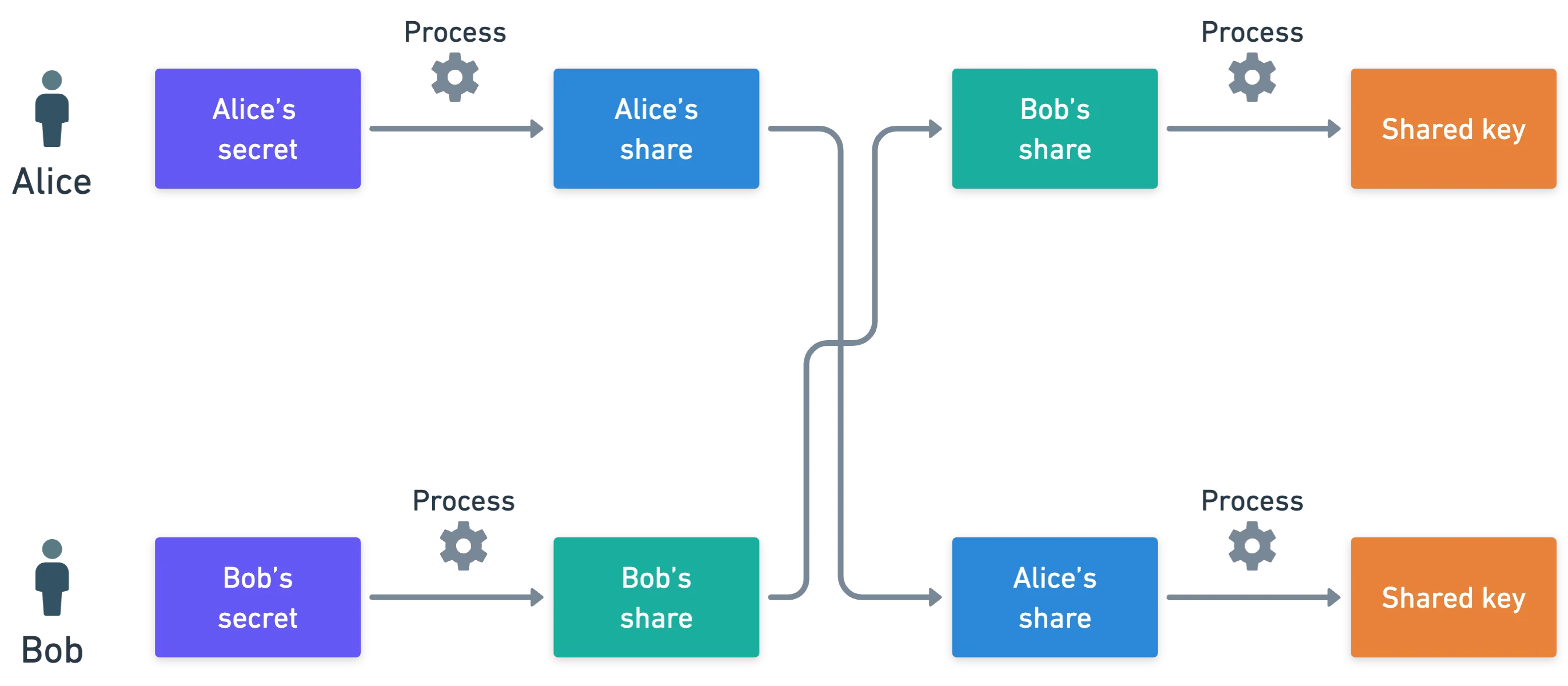
A ideia é simples: André e Bruna querem combinar seus segredos individuais, para produzir uma chave compartilhada.

Criando o Segredo Compartilhado

Para fazer isso, André e Bruna concordam em usar uma curva elíptica, e algum gerador $G$ para a curva. Digamos que André escolhe um inteiro secreto $a$, e Bruna escolhe outro inteiro secreto $b$. Como eles os combinam?  - André calcula $A = [a]G$, e envia isso para Bruna. Lembre-se que Bruna não pode possivelmente recuperar $a$ de $A$ — é extremamente difícil.

• Bruna recebe $A$, e calcula $S = [b]A = [b]([a]G) = [b.a]G$.

Bruna também envia $B = [b]G$, e André também calcula $S = [a]B = [a]([b]G) = [b.a]G$. E olha só — eles calcularam o mesmo ponto $S$!

O legal disso é que qualquer um interceptando as comunicações entre André e Bruna obteria apenas $A$ ou $B$. E sozinhos, esses pontos não significam nada.

Assim, eles criaram com segurança uma chave compartilhada! Sensacional. Só lembre-se de manter a chave gerada segura!

Esquemas de Compromisso

Ok, sabemos como gerar uma chave compartilhada com segurança. O que mais podemos fazer?

Outra ideia é a de comprometer-se a um valor antes do tempo. E para ilustrar, vamos jogar pedra-papel-tesoura. Mas vamos jogar em turnos. É assim que seria:

André joga pedra. Então Bruna joga papel. Vitória mais fácil da vida dela.

Obviamente, o problema aqui é que André revelou sua jogada antes do tempo. E se ele pudesse esconder sua jogada?

Click to zoom

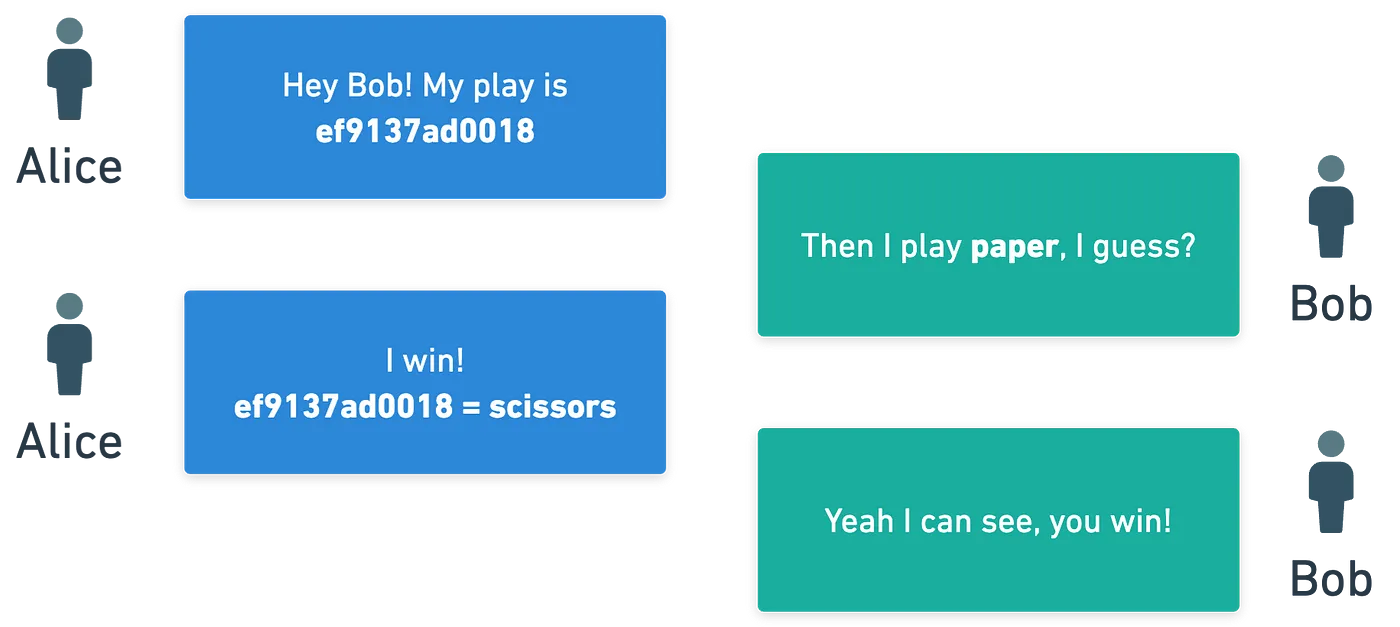
André produz algum valor que está vinculado à sua jogada (tesoura), mas que também esconde sua decisão. Isso é conhecido como um compromisso. Mais tarde, André revela o valor original, e Bruna verifica se corresponde ao compromisso. É realmente como colocar sua jogada em um envelope selado, e abri-lo quando necessário.

Eu sei o que você está pensando: por que diabos alguém jogaria pedra-papel-tesoura dessa forma? Eu realmente não sei. Mas esse não é o ponto — podemos usar essa ideia para criar protocolos úteis.

Criando o Compromisso

Vamos construir o que é chamado de compromisso de Pedersen. Este tipo de esquema requer uma etapa de configuração, que deve retornar um gerador $G$ de uma curva elíptica, e algum outro ponto $H = [k]G$.

$$\textrm{setup}() \rightarrow (G, H)$$

Então, se André quer se comprometer com alguma mensagem $M$, ele segue estes passos:

• Ele faz o hash do valor para um inteiro $h(M)$,
• Ele então escolhe um inteiro aleatório $r$, também chamado de fator de ofuscação,
• Finalmente, ele calcula $C = [r]G + [h(M)]H$. Este será seu compromisso.

O compromisso $C$ pode ser compartilhado com qualquer um, porque é oculto: não revela informação sobre a mensagem. Mais tarde, André pode compartilhar os valores secretos $M$ e $r$, e qualquer um (por exemplo, Bruna) pode recalcular C e verificar se corresponde ao que André compartilhou — dizemos que André abre o compromisso.

Formalmente, dizemos que um esquema de compromisso deve ser:

• Oculto: não deve revelar informação sobre a mensagem comprometida.
• Vinculante: o compromisso só pode ser aberto com o $M$ e $r$ originais. Caso contrário, deve ser inválido.

E finalmente, e quanto ao fator de ofuscação? Se não o usássemos, então $C$ sempre se pareceria com isso: $C = [h(M)]H$. Isso não é bom, porque a função de hash é determinística: sempre produzirá o mesmo resultado para uma entrada fixa.

Então, assim que você vê dois compromissos idênticos, você imediatamente sabe que eles estão associados à mesma informação — e se você já conhece os dados secretos, então o compromisso não está oculto de forma alguma! Lembre-se:

Uma corrente é tão forte quanto seu elo mais fraco

A introdução de um fator de ofuscação aleatório resolve este problema. Em geral, esta ideia de introduzir aleatoriedade em esquemas é usada para prevenir vulnerabilidades baseadas em repetição, como a que acabamos de descrever.

Esquemas de compromisso são uma pedra fundamental para construções mais poderosas que exploraremos em artigos posteriores.

Assinaturas

Já cobrimos um exemplo de assinaturas usando curvas elípticas, chamado Elliptic Curve Digital Signature Algorithm (ou ECDSA para abreviar). Mas existem outras maneiras de criar assinaturas.

Em particular, existe outro protocolo chamado assinatura de Schnorr. E com toda honestidade, é mais simples que ECDSA. Pensando bem, talvez devêssemos ter coberto isso em vez de ECDSA. É. Desculpe por isso.

De qualquer forma, a assinatura de Schnorr é frequentemente apresentada usando o grupo aditivo de inteiros módulo $q$, mas como mencionamos anteriormente, qualquer construção com dito grupo pode ser adaptada para curvas elípticas. E é isso que demonstraremos agora.

A configuração é a mesma de antes, no ECDSA: André mantém uma chave privada $d$, e Harold (desculpe Bruna, devemos pelo menos isso a ele) mantém a chave pública associada $Q = [d]G$, onde $G$ é um gerador do grupo que André e Harold concordaram em usar.

Para assinar, André faz o seguinte:

• Ele escolhe um inteiro aleatório $r$, e calcula $R = [r]G$.
• Então, ele calcula o hash $e = H(R || M)$. Aqui, o $||$ representa concatenação bit a bit — então essencialmente ele só faz hash de um monte de zeros e uns. Ah, e $e$ é um inteiro.
• Finalmente, ele calcula $s = r - e.d$.

A assinatura é o par $(s, e)$. Para verificar, Harold segue este procedimento:

• Ele calcula $R' = [s]G + [e]Q$,
• E ele aceita se $e = H(R' || M)$.

Simples, né? Desta vez, não precisamos calcular nenhum inverso multiplicativo modular. E é bastante direto verificar que $R'$ deve corresponder a $R$:

$$R' = [s]G + [e]Q = [r - e.d + e.d]G = [r]G = R$$

Assinaturas de Schnorr oferecem uma alternativa ao ECDSA mais estabelecido. Na verdade, elas são mais simples de implementar, não dependem de inversos multiplicativos modulares, e teoricamente oferecem mais segurança. Algumas blockchains como Polkadot já adotaram este esquema de assinatura; no final, cabe a você decidir o que usar.

Provas de Conhecimento Zero

Provas de conhecimento zero (ZKPs para abreviar) têm sido um tópico quente nos últimos anos. Elas não são uma descoberta nova de forma alguma, mas receberam muito interesse por causa de suas propriedades, e das coisas legais que podem ser feitas com elas.

Essencialmente, uma ZKP é uma maneira de demonstrar ou provar conhecimento de algo, sem revelar nada sobre isso. Parece maluco, né? Como posso te dizer que sei algo sem te dizer o que é esse algo?

Aqui está um excelente vídeo que mostra alguns ótimos exemplos de ZKPs.

O exemplo que eu mais amo é a prova do Onde está Wally: o que eu quero provar é que eu sei onde o Wally está. Uma opção é simplesmente apontar para ele — mas isso efetivamente revelaria sua localização!

Para não revelá-la, posso fazer o seguinte: pegar um pedaço grande de papelão, fazer um buraco nele do tamanho do Wally, e colocá-lo sobre o livro. Você pode ver o Wally através do buraco, mas não pode ver onde ele está colocado na página!

O Protocolo de Schnorr

Claramente, não vamos construir um sistema de prova de localização do Wally com curvas elípticas. Teremos que nos contentar com algo muito mais simples: provar conhecimento do logaritmo discreto de um ponto. Isso é, provar que sabemos algum valor $x$, tal que $Y = [x]G$, com $G$ sendo um gerador de um grupo de curva elíptica. O grupo tem ordem $n$.

O que estamos prestes a descrever é chamado de protocolo de Schnorr, adaptado para curvas elípticas. É um protocolo muito simples e elegante, e fornece uma ótima base para provas de conhecimento mais complexas.

Aqui está Claus P. Schnorr, por sinal. Mandando bem com seus 80 anos de idade. Que lenda.

É assim que o protocolo funciona: André, que chamaremos de prover, quer provar que ele sabe $x$. Bruna, a verifier, sabe $Y$. Claro, André poderia divulgar o valor de $x$, e Bruna poderia verificar que é de fato o logaritmo discreto de $Y$ ($Y = [x]G$). Mas por qualquer motivo, digamos que $x$ deve permanecer privado.

André e Bruna interagem da seguinte forma:

• André primeiro escolhe algum inteiro aleatório $r$, e calcula $R = [r]G$. Este é um compromisso que ele então envia para Bruna.
• Bruna escolhe algum outro inteiro $c$ aleatoriamente, e o envia para André.
• André então calcula:

$$s = (r + c.x) \ \textrm{mod} \ n$$

• Bruna recebe $s$, e verifica se:

$$[s]G = R + [c]Y$$

Vou deixar a matemática para você verificar!

O interessante é que, se por algum motivo Bruna não estiver convencida depois disso, ela pode enviar um valor novo de $c$ para André, e repetir o processo. Na verdade, ela pode fazer isso quantas vezes quiser até estar satisfeita. Isso sugere a ideia de alguns protocolos criptográficos serem interativos, um fato ao qual voltaremos mais tarde na série.

Funções Aleatórias Verificáveis

Outra coisa legal que podemos fazer é gerar números aleatórios de uma forma verificável.

O quê?

Esta soa maluca. Acredito que uma analogia pode ajudar.

Suponha que você compre um bilhete de loteria. Você vai a uma loja, escolhe alguma combinação aleatória de números, e recebe o bilhete associado.

Então o vencedor da loteria é selecionado, e por acaso é seu número! Como você prova que é o vencedor? Bem, claro, você tem o bilhete! Então você só o apresenta na casa da loteria, e recebe seu prêmio!

Embora esta analogia não seja perfeita, ela transmite uma mensagem importante: pode haver coisas para provar sobre números gerados aleatoriamente.

Funções aleatórias verificáveis (ou VRFs para abreviar) fazem exatamente isso: elas geram um número pseudoaleatório baseado em alguma entrada de um usuário, e também fornecem uma prova de que o processo de geração foi honesto e correto. Discutiremos isso em mais detalhes em artigos posteriores, então por enquanto, vamos nos concentrar em uma implementação de VRFs usando apenas curvas elípticas.

Então, a intenção ao criar uma VRF é a seguinte: André quer gerar um número pseudoaleatório, que Bruna pode verificar. Eles concordam em um gerador de curva elíptica $G$ para um grupo de ordem $n$, e também concordam em dois algoritmos: $h$ e $h'$. O primeiro faz hash para um número, como de costume, mas o último faz hash para um ponto na curva elíptica.

A configuração não diverge muito do usual: André tem uma chave privada $d$, e uma chave pública $Q = [d]G$. No entanto, há um elemento extra aqui: a entrada $a$ para a VRF é publicamente conhecida. Todos executarão o mesmo número através de suas VRFs independentes, e produzirão saídas diferentes.

Agora, existem dois passos para o algoritmo: uma etapa de avaliação, onde o número aleatório é produzido junto com uma prova, e a etapa de verificação. André realiza a avaliação da seguinte forma:

• Ele calcula $H = h'(Q, a)$. Este é um ponto na curva elíptica.
• Então ele calcula $Z = [d]H$, a saída da VRF.
• Agora ele tem que produzir uma prova. Ele escolhe um número aleatório $r$, e calcula $U = [r]G$, e $V = [r]H$.
• Ele faz hash de tudo em um número $c$:

$$c = h(H || Z || U || V)$$

• Finalmente, ele calcula $s$:

$$s = r + d.c \ \textrm{mod} \ n$$

O resultado da avaliação da VRF é $\pi = (Z, c, s)$, onde $Z$ é a saída pseudoaleatória real, e os outros valores funcionam como uma prova de correção de $Z$.

Finalmente, Bruna precisa verificar a prova. É isso que ela faz:

• Ela calcula o mesmo hash que André calculou, $H = h'(Q, a)$. Ela pode fazer isso porque tanto $Q$ quanto $a$ são públicos.
• Então ela calcula $U'$ e $V'$ como mostrado abaixo. Você pode verificar que estes resultam no mesmo $U$ e $V$ de antes.

$$\\ U' = [s]G - [c]Q \\ V' = [s]H - [c]Z$$

 - Finalmente, ela calcula $c' = h(H || Z || U' || V')$, e aceita a prova se $c = c'$.

Ufa. Ok. Isso foi muito. Vamos desempacotar.

A ideia é que a saída $Z$ é imprevisível devido à natureza da função de hash, mas é determinística mesmo assim. Por causa disso, somos capazes de produzir uma assinatura curta que só pode funcionar com conhecimento da chave privada, $d$.

A utilidade das VRFs pode não ser imediatamente evidente, mas elas podem ser uma ferramenta poderosa para a aplicação certa. Por exemplo, Algorand usa VRFs como parte de seu mecanismo central de consenso. E quem sabe que aplicações malucas você pode encontrar para elas! O mundo é sua ostra, desde que você tenha as ferramentas certas.

Resumo

Como você pode ver nos métodos que exploramos, algumas ideias se repetem vez após vez. Na maioria dos casos, realizamos duas operações que produzem o mesmo resultado. Também começamos com um par de chaves privada/pública na maioria das vezes. Usamos funções de hash para mapear dados em conjuntos de interesse.

Combinar essas ideias básicas permite a criação de protocolos interessantes e úteis, e é só isso. Aplicações mais complexas podem exigir "jogos" criptográficos mais complexos.

E é claro, existem ainda mais coisas divertidas que podemos fazer com curvas elípticas. Por exemplo, existem esquemas de assinatura mais sofisticados — como assinaturas cegas, assinaturas em anel, assinaturas de limiar, entre outros. Cobriremos esses no próximo artigo.