Criptografia 101: Curvas Elípticas (Parcialmente) Desmistificadas

Este é parte de uma série maior de artigos sobre criptografia. Se este é o primeiro artigo que você encontra, recomendo fortemente começar pelo início da série.

No artigo anterior, discutimos brevemente algumas das ideias que sustentam boa parte das técnicas criptográficas mais amplamente utilizadas.

Ainda não discutimos por que os grupos e a aritmética modular são úteis para criptografia. Mas como você pode imaginar, a ideia geral é que eles nos permitem criar problemas que são tão difíceis de resolver, que é praticamente impossível quebrá-los mesmo à custa de quantidades impressionantes de recursos computacionais. Então, por exemplo, por que uma assinatura digital funciona? Bem, porque produzir uma assinatura válida é relativamente simples com o conhecimento de uma chave secreta, mas incrivelmente difícil sem ela.

Lidaremos com essas considerações mais tarde. Por enquanto, acredito ser mais produtivo focar em outros grupos que ajudam a tornar os problemas a serem resolvidos ainda mais difíceis — e é aqui que as curvas elípticas entram em cena.

O que são Curvas Elípticas?

Uma curva geralmente é definida por uma equação. No caso das curvas elípticas, a equação $E$ (que na verdade é uma forma reduzida, mas vamos com ela) se parece com isso:

E: y^2 = x^3 + ax + b

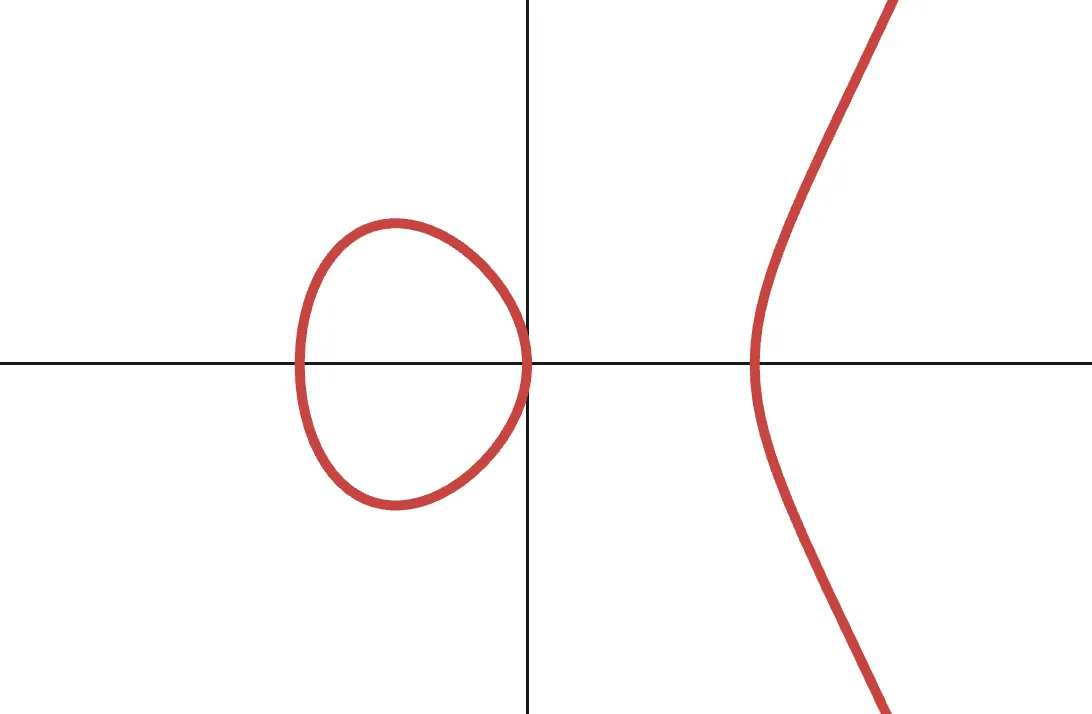
Uma curva elíptica — Um gráfico da curva y² = x³ - x

Mas espere... O que isso tem a ver com grupos? Isso é apenas uma curva, afinal!

Vamos recapitular o que aprendemos até agora, né? Um grupo é definido por um conjunto (vamos chamá-lo de $\mathbb{G}$ ) e uma operação binária envolvendo dois elementos de $\mathbb{G}$ e produzindo uma saída que também está em $\mathbb{G}$ . Se pudermos pensar em uma maneira de usar curvas elípticas para obter um conjunto e uma operação binária válidos, então encontramos para nós um grupo.

E com certeza, existe algo que podemos fazer!

•••

A Operação de Grupo

Pegue dois pontos $P$ e $Q$ na curva elíptica, e desenhe uma linha através desses pontos. Algumas substituições básicas mostram que existirá (quase sempre) um terceiro ponto de interseção. Então pegue esse ponto, imagine que o eixo $x$ é um espelho, e reflita-o verticalmente. Parabéns, você acabou de chegar ao ponto $R = P + Q$ !

Esse processo é chamado de regra da corda e tangente. E é, de fato, a operação de grupo que estamos procurando.

A primeira vez que vi isso, lembro-me de pensar "que processo tão estranho". Lembro-me de perguntar a mim mesmo: por que diabos você precisa virar o terceiro ponto de interseção? E depois de investigar mais a fundo o assunto, tudo o que posso dizer é: explicar o motivo pelo qual isso faz sentido está muito fora do escopo deste artigo. Só vou pedir que você confie em mim que tudo é perfeitamente lógico, pelo menos por agora.

Diagrama de corda e tangente — A curva elíptica y² = x³ - x + 1 (vermelha) com uma representação da operação P + Q = R

Você pode tentar isso você mesmo em uma ferramenta gráfica como Desmos ou GeoGebra.

Um componente pronto, ainda falta mais um — também precisamos de um conjunto. E como a regra da corda e tangente mapeia dois pontos na curva elíptica para outro, segue naturalmente que estaremos trabalhando com um conjunto de pontos na curva elíptica. Mas existem dois problemas com isso, a saber:

A maioria dos pontos na curva elíptica são de valor real, o que significa que as coordenadas podem não ser inteiros. E é importante que o sejam: caso contrário, podemos ter erros de arredondamento ao calcular $P + Q$ .
Há um número infinito de pontos na curva, e estamos atrás de um conjunto finito.

Então, como resolvemos esses problemas?

Encontrando um Conjunto Adequado

Acontece que algumas curvas elípticas têm um número infinito de pontos com valores inteiros, isto é, pontos como $P = (1,2)$ . Por causa disso, nosso primeiro problema desaparece de maneira um tanto mágica com uma seleção adequada de curva elíptica. Vamos supor que sabemos como fazer isso e focar no segundo problema.

Existe um truque interessante para transformar uma quantidade infinita de inteiros em um conjunto finito, e já vimos isso em ação. Consegue adivinhar? Isso mesmo, a operação de módulo!

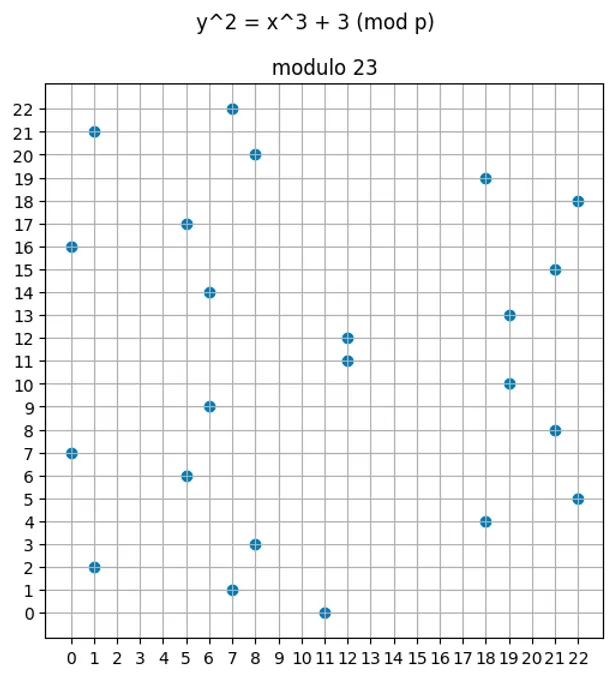
Como uma curva elíptica sobre os inteiros (módulo 23) se parece — Os pontos de uma curva elíptica, módulo 23

Formalmente, dizemos que a curva elíptica é definida sobre um campo finito, então qualquer ponto que esteja "fora do intervalo" é mapeado de volta para o intervalo com a operação de módulo. Isso é denotado como:

E(\mathbb{F_q}) \ / \ \mathbb{F}_q = \{0,1,2,3,...,q-1\}

E pronto! Agora temos um conjunto e uma maneira de calcular o resultado de "adicionar" dois pontos. Mas será que temos mesmo? Está faltando algo...

A Identidade do Grupo

Dê uma olhada na imagem a seguir. O que acontece se tentarmos adicionar $P + Q$ neste cenário?

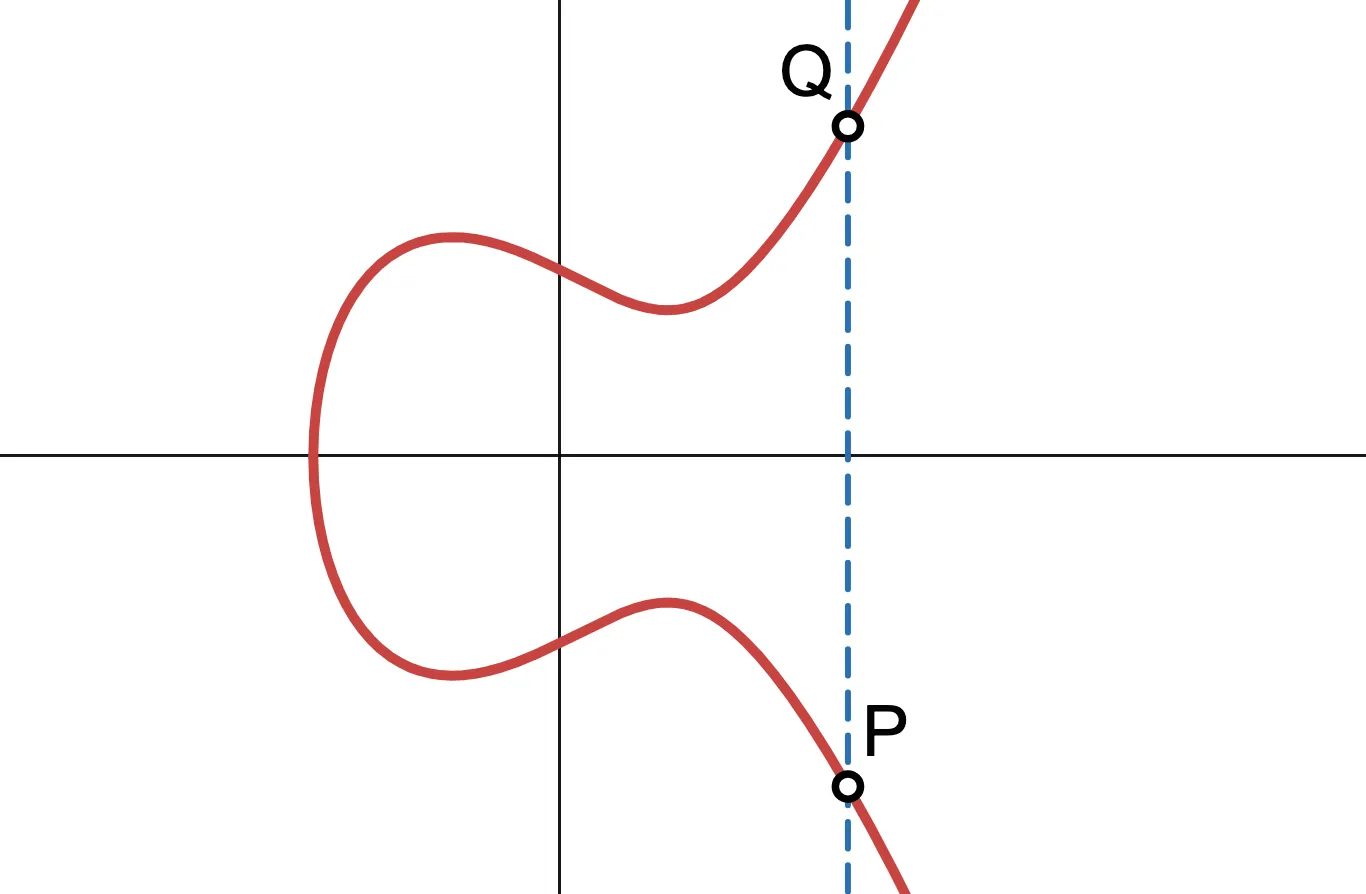
Dois pontos verticalmente alinhados sendo somados

Podemos ver imediatamente que não há um terceiro ponto de interseção! O pânico se instala. Isso significa que nossa construção não funciona?

Felizmente, a crise é rapidamente evitada definindo um novo elemento de grupo, denotado $\mathcal{O}$ . Pense nele como um ponto no infinito — o que não é realmente o que acontece, mas pode ajudar na conceituação. Este novo elemento tem uma propriedade interessante, dado qualquer ponto $P$ na curva:

P + \mathcal{O} = \mathcal{O} + P = P

Isso não lembra algo? Não é exatamente o que acontece quando adicionamos zero a qualquer número?

De fato, esse comportamento é importante na teoria dos grupos — o papel que o zero desempenha no grupo dos inteiros, e o papel que o $\mathcal{O}$ desempenha nas curvas elípticas é o de identidade dos respectivos grupos. Adicionar este elemento ao nosso conjunto o torna completo — e agora podemos adicionar dois pontos e sempre ter um resultado válido.

Mas ainda não terminamos. Há mais um pequeno detalhe que precisamos cobrir.

Duplicação de Pontos

O que acontece se tentarmos adicionar $P + P$ ? Para tentar seguir a regra da corda e tangente: precisamos de uma linha através dos dois pontos na operação, mas aqui... Só existe um! Assim, como o nome sugere, precisaremos considerar a linha tangente à curva elíptica em $P$ .

Como antes, encontramos outro ponto de interseção, invertemos, e encontramos $P + P$ , que convenientemente denotaremos $[2]P$ . Num absoluto golpe de inspiração, esta operação foi nomeada duplicação de ponto.

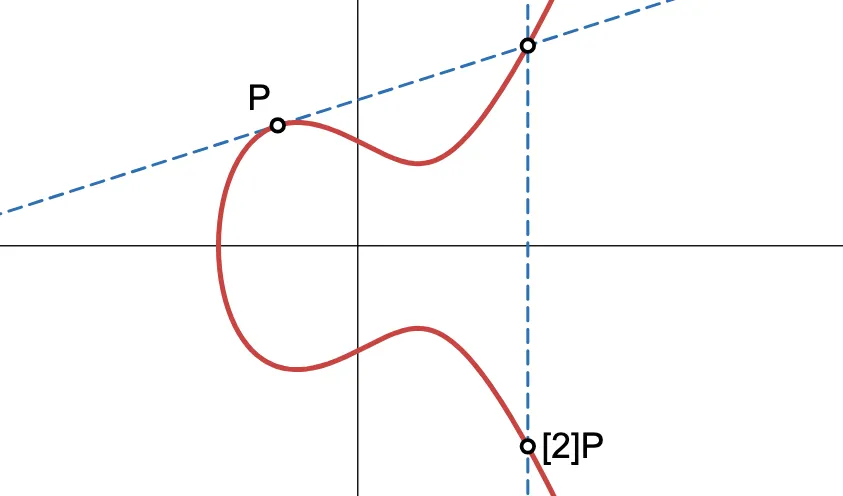
Calcular $P + [2]P$ então procede como de costume: desenhe uma linha através dos dois pontos, inverta o terceiro ponto de interseção, e voilà! Você acabou de obter $[3]P$ . Faça isso novamente, e você terá $[4]P$ . E aqui, podemos observar algo peculiar: adicionar $P$ quatro vezes ( $P + P + P + P$ ) produz o mesmo resultado que adicionar $[2]P + [2]P$ !

Por mais inocente que a afirmação anterior pareça, é na verdade a ferramenta mais poderosa que temos ao trabalhar com curvas elípticas. Suponha que queremos calcular $[12384162178627301263]P$ . Fazer isso um ponto de cada vez levaria muito tempo — mas aplicando corretamente a duplicação de pontos, o resultado pode ser obtido exponencialmente mais rápido!

Isso sugere os problemas extremamente difíceis que foram mencionados no início deste artigo. E como discutiremos em breve, este é precisamente o tipo de problemas difíceis que permitem que construções criptográficas baseadas em grupos existam!

•••

Resumo

Acabamos de definir grupos de curva elíptica. São apenas um monte de pontos inteiros, que podemos adicionar, e que estão dentro de um intervalo graças à operação de módulo. Geralmente, quando as curvas elípticas são mencionadas na literatura, significa o grupo, não a curva. Se a curva precisa de menção específica, é frequentemente chamada de curva afim.

Se você se sente assim agora:

Meme 'Não tenho ideia do que estou fazendo' — Eu todas as manhãs

Tudo o que posso dizer é que isso pode ser difícil de assimilar no primeiro contato, mas uma vez que se estabelece, parece bastante natural. Dê um tempo, e não hesite em perguntar se tiver alguma dúvida!

Além disso, você pode brincar com curvas elípticas neste site.

Nossa base está pronta. No próximo artigo, examinaremos o que podemos fazer com nosso conhecimento de curvas elípticas. Veremos um esquema para encriptação assimétrica e outro para assinaturas digitais. Fique ligado!