Criptografia 101: Encriptação e Assinaturas Digitais

Este é parte de uma série maior de artigos sobre criptografia. Se este é o primeiro artigo que você encontra, recomendo fortemente começar pelo início da série.

No artigo anterior, expandimos nosso conhecimento básico de grupos definindo grupos de curva elíptica. E mencionamos brevemente que esses conceitos nos permitiriam construir alguns mecanismos criptográficos úteis.

E conforme prometido, vamos dar uma olhada em dois exemplos básicos dessas técnicas: um para assinatura digital e outro para encriptação. Mas antes de fazermos isso, precisamos definir alguns dispositivos que serão essenciais em nosso desenvolvimento. Trabalharemos no contexto de curvas elípticas, mas esses conceitos podem ser generalizados para outros grupos.

Você provavelmente já ouviu falar de chaves privadas e públicas. Vamos ver o que elas realmente são.

Pares de Chaves

A história que geralmente é contada ao aprender sobre assinaturas digitais é mais ou menos assim: um usuário (digamos, André) com uma chave privada (ou secreta) pode assinar uma mensagem, e então qualquer pessoa pode verificar a assinatura com a chave pública associada.

E claro, não aprendemos nada sobre os mecanismos por trás disso. Mas há uma mensagem implícita: não deveria ser possível obter uma chave privada a partir de uma chave pública, pois isso significaria que qualquer pessoa com a chave pública de André poderia produzir uma assinatura em nome de André (afinal, é chamada de privada por uma razão). Com isso em mente, vamos ver o que essas chaves realmente são.

Click to zoom

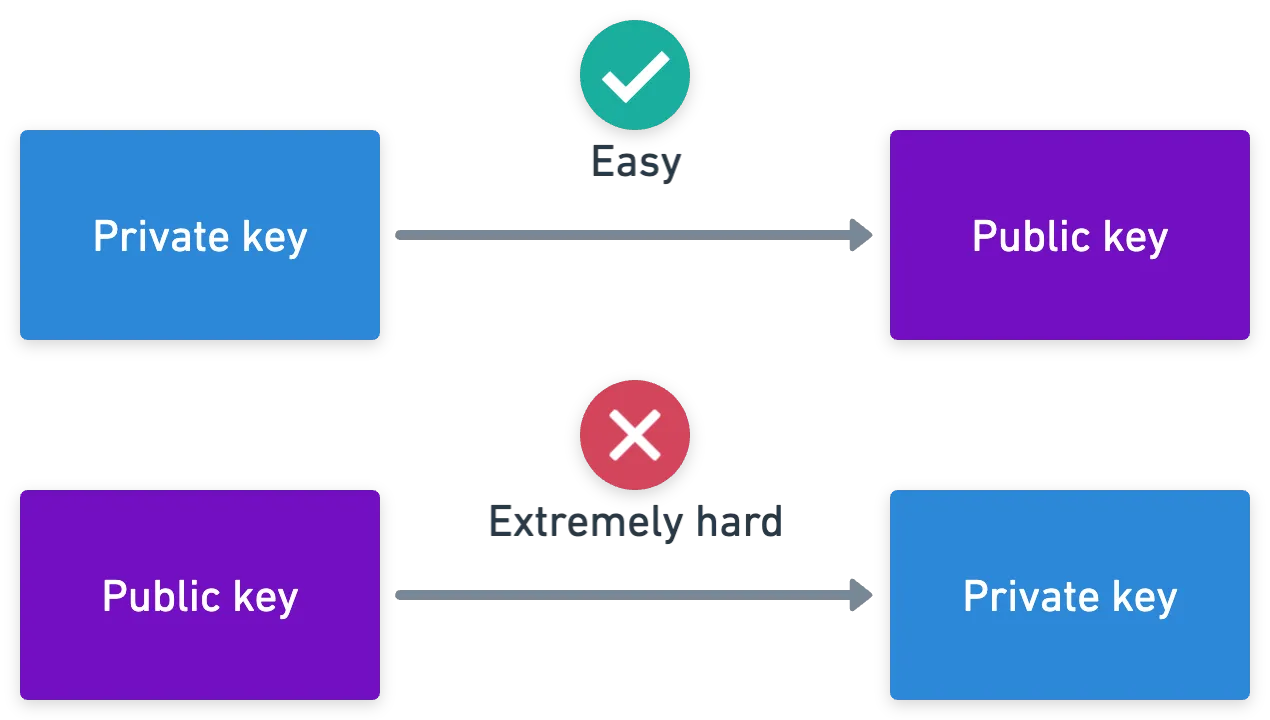
Lembra dos geradores de grupo do primeiro artigo? Pois é, é aqui que eles entram. As curvas elípticas, sendo grupos, também têm geradores e subgrupos!

Suponha que André e outra pessoa, Bruna, concordem com um ponto gerador $G$ na curva elíptica. André então escolhe algum número aleatório $d$ do conjunto de inteiros módulo $q$, então $d < q$. Além disso, vamos assumir que $d$ é um número grande, não apenas $12$ ou $35$. Este será sua chave privada.

André prossegue calculando $Q = [d]G$, aproveitando o poder da duplicação de pontos, e obtém outro ponto no grupo — esta será sua chave pública, e ele pode enviá-la com segurança para Bruna.

Evidentemente, $Q$ codifica informações sobre a chave privada. Bruna poderia tentar calcular um número $d$ tal que $Q = [d]G$ — mas o problema é que, se nosso grupo de curva elíptica for "grande o suficiente", isso levaria um tempo realmente, realmente longo. E este é precisamente o segredo: encontrar $d$, mesmo conhecendo $Q$ e $G$, deveria ser quase impossível. Isso é conhecido como (uma versão do) problema do logaritmo discreto (DLP).

Claro, se nosso grupo tiver $1000$ elementos, ou se o número que André escolhe for "pequeno", tentar valores possíveis de $d$ é uma tarefa factível. Você provavelmente pode escrever um script que resolve o problema em menos de 10 minutos — isso é chamado de força bruta. O problema DLP realmente brilha quando temos grupos enormes. Por exemplo, a curva 25519 tem subgrupos de ordem em torno de $~2^{250}$. Isso é um número bem grande. Boa sorte tentando encontrar $d$ por força bruta.

Encriptação

André agora possui um número $d$ como sua chave privada, e Bruna possui a chave pública correspondente $Q$, que é apenas um ponto na curva elíptica. O que eles podem fazer com isso?

Esses dispositivos que desenvolvemos são suficientes para começar a construir coisas divertidas (eba!). Vamos encriptar alguns dados!

Imagine que Bruna queira proteger uma mensagem para que apenas André possa lê-la. Se eles fossem adolescentes na escola, poderiam trocar uma mensagem escrita em um código secreto que só André e Bruna conseguem entender. Como ambos conhecem o código secreto, ambos podem "desfazer" a codificação — então isso é chamado de encriptação simétrica.

Certo, parece simples o suficiente!

Como isso acontece em uma aplicação real? Pense nisso: qualquer mensagem é apenas um monte de zeros e uns, algum número binário. Se distorcermos esse número, essencialmente o transformamos em uma bobagem sem sentido — isso geralmente é chamado de texto cifrado. E se fizermos isso de forma reversível, a mensagem original pode ser recuperada!

Click to zoom

Aqui está uma implementação simples caso você queira brincar com isso.

Só para esclarecer, a reversibilidade aqui é dada pela operação lógica XOR. Não se preocupe com isso - o ponto é que conseguimos mascarar a mensagem original, com uma chave secreta compartilhada.

E as Curvas Elípticas?

Claramente, não precisávamos de curvas elípticas na construção anterior. E isso mostra que a criptografia é muito mais ampla do que apenas uma única ferramenta, e realmente data de muito antes das curvas elípticas serem sequer uma coisa.

Mas o que acontece com a chave secreta? Como André e Bruna concordam em uma chave compartilhada? Se eles fizerem isso de maneira insegura, então outra pessoa poderia estar ouvindo, e essa terceira pessoa (digamos Charlie) pode então ler as mensagens secretas de André e Bruna! Nada legal, nossa encriptação se torna inútil!

Vamos não entrar em pânico ainda. Embora existam maneiras de compartilhar chaves secretas com segurança, há outra solução: podemos usar curvas elípticas para obter o segredo compartilhado de maneira assimétrica.

Encriptação Assimétrica

Digamos que Bruna queira encriptar uma mensagem $M$ para André. Em vez de concordarem com uma chave, André pode simplesmente escolher uma chave privada $d$ e compartilhar sua chave pública $Q = [d]G$ com Bruna. Com essa configuração, podemos criar uma maneira para Bruna encriptar mensagens apenas para André. É assim que funciona:

• Ela escolhe algum número aleatório $k < q$, geralmente chamado de nonce,
• Bruna então calcula $[k]Q$ e usa isso para calcular uma máscara, que denotaremos $P$, usando algum algoritmo acordado previamente,
• Ela mascara a mensagem usando XOR como no exemplo anterior, e obtém o texto cifrado $C = M + P$,
• Finalmente, ela calcula $[k]G$, onde $G$ é o gerador do grupo que André e Bruna concordaram previamente,
• Bruna então envia o par de pontos $([k]G, C)$ para André.

André, que conhece a chave privada $d$, pode então realizar estas ações:

• Ele calcula $[d]([k]G)$. Não mencionamos isso, mas a multiplicação é comutativa em curvas elípticas, então $[d]([k]G) = [k]([d]G) = [k]Q$. Sem conhecimento de $k$, ainda podemos reconstruir a máscara que Bruna usou. Incrível.
• Usando o algoritmo acordado, André calcula a máscara e reverte o mascaramento com $M = C + P$.

Visuais tendem a ajudar muito. No geral, o processo se parece com isso:

Click to zoom

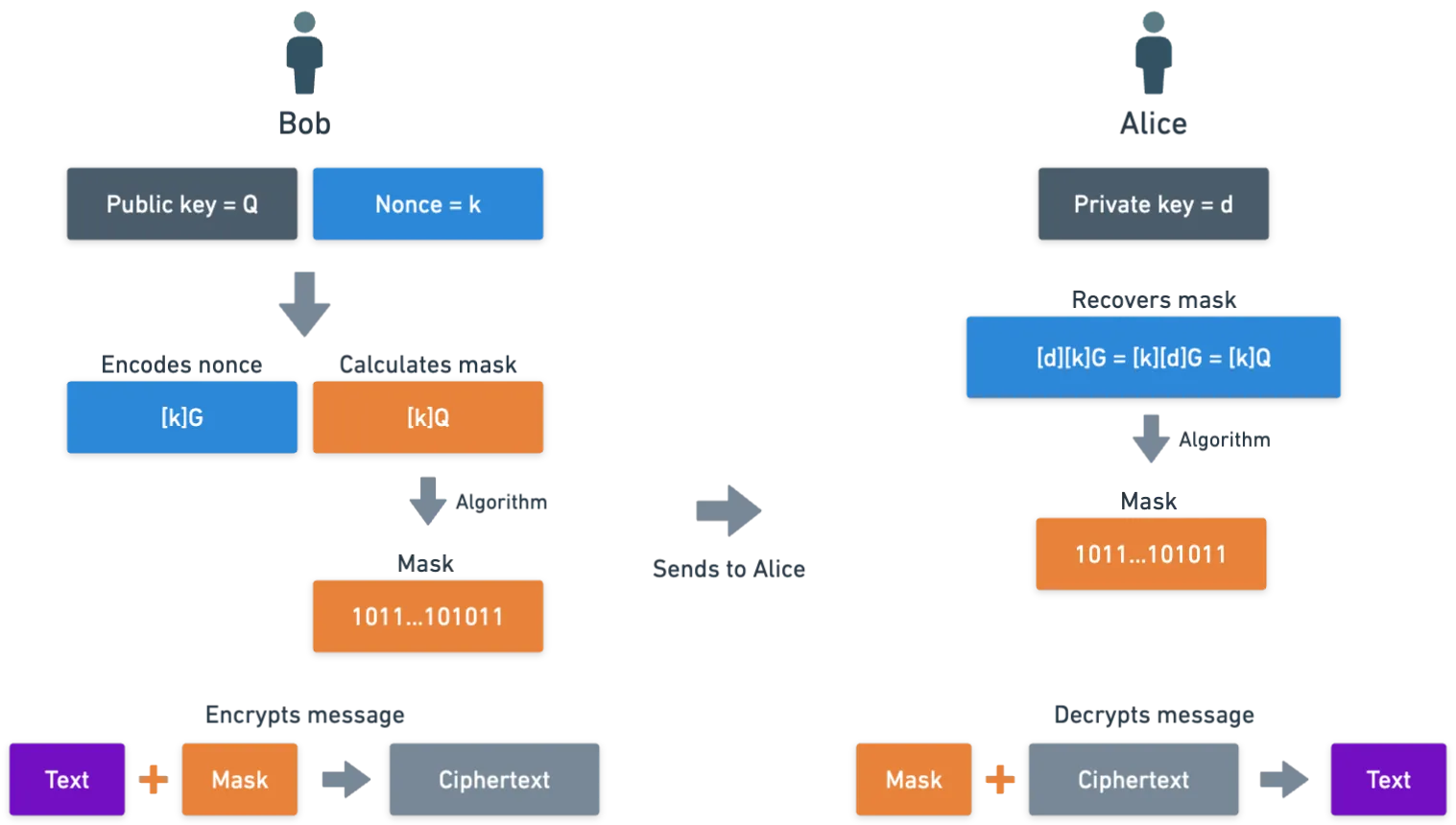
Este processo é chamado de Esquema de Encriptação Integrada de Curva Elíptica, ou ECIES para abreviar. Existem outros esquemas semelhantes, como o sistema de encriptação de ElGamal, que pode ser adaptado para curvas elípticas.

Não sei quanto a você, mas eu acho isso fascinante. Com apenas algumas operações, é possível proteger dados de uma forma que é impossível de decifrar na prática sem o conhecimento de um único número (que só André conhece).

Nosso entendimento de grupos está finalmente dando frutos!

Resumindo:

Este método de encriptação funciona calculando uma máscara e adicionando-a à mensagem original.

Na encriptação simétrica, ambas as partes precisam conhecer a máscara; na encriptação assimétrica, o desmascaramento só pode ser feito com o conhecimento de uma chave privada por uma das partes.

Assinaturas Digitais

A encriptação assume que a informação codificada deve permanecer secreta para leitores não intencionais. Isso nem sempre é verdade: às vezes a informação pode ser pública, mas nosso interesse está em provar sua autenticidade. Por exemplo:

Suponha que Bruna queira enviar uma solicitação de pagamento para André no valor de $1000. Ela envia para André o número de sua conta bancária e o valor que precisa transferir. O que aconteceria se outra pessoa (digamos Charlie) interceptasse a mensagem e mudasse a conta bancária de Bruna pela dele?

André não tem como verificar se a conta bancária é de Bruna ou de Charlie. Há algo que possamos fazer para impedir que Charlie use essa estratégia para roubar o dinheiro?

Se Bruna pudesse de alguma forma assinar a informação, então André poderia verificar que a assinatura é válida e aceitar a mensagem. Por sua vez, se Charlie mudar a conta bancária, a assinatura não será mais válida, e André rejeitaria a mensagem. Esta é exatamente a funcionalidade que as assinaturas digitais fornecem.

O que apresentaremos agora é chamado de Algoritmo de Assinatura Digital de Curva Elíptica, ou ECDSA para abreviar. Este processo é talvez um pouco mais complicado que a encriptação. Envolverá algumas novas ginásticas matemáticas. Vamos defini-las conforme necessário. Segure-se.

• Bruna codifica sua mensagem, como fez no exemplo de encriptação, mas desta vez a saída é um inteiro $M$. Veremos como fazer isso mais tarde.
• Bruna então escolhe um número aleatório $k$, assim como no caso da encriptação,
• Ela também calcula $R = [k]G$. Denotaremos a coordenada x de $R$ pela letra $r$,
• O último cálculo que ela realiza é para o número $s$, calculado como:

$$s = k^{-1}(M + d.r) \ \textrm{mod} \ n$$

• E finalmente, ela envia o par $(r, s)$ para André.

O $k^{-1}$ no cálculo de $s$ não é o recíproco de $k$ (isto é, não é $1/k$).

Em vez disso, $k^{-1}$ representa o inverso multiplicativo modular. Essencialmente, é um número que, quando multiplicado por $k$, produz o seguinte resultado:

$$k.k^{-1} \ \textrm{mod} \ n = 1$$

Além disso, o módulo (n) é um número especial: é a ordem do ponto gerador $G$. Cada ponto na curva elíptica tem uma ordem, que é o menor inteiro para o qual $[n]G = \mathcal{O}$. Esta também é a ordem do grupo $\mathbb{G}$.

Ok, isso foi complicado, mas temos nossa assinatura. Tudo o que resta é verificá-la. Como a mensagem é pública, André pode codificá-la para o mesmo número $M$ que Bruna usou. E então, ele segue estes passos:

• Ele calcula $w$ como o inverso modular de $s$, então $w = s^{-1} \ \textrm{mod} \ n$.
• André então pega esse valor e calcula $R' = [w.M]G + [w.r]Q$.
• Ele aceita a assinatura se a coordenada x de $R'$ corresponder ao valor $r$.

Trabalhar com os números e verificar que $R' = R$ é um bom exercício para o leitor. Se você vai tentar, apenas lembre que, como $G$ é um gerador de ordem n, então $[n]G = \mathcal{O}$. Você também pode precisar usar algumas propriedades da aritmética modular.

Click to zoom

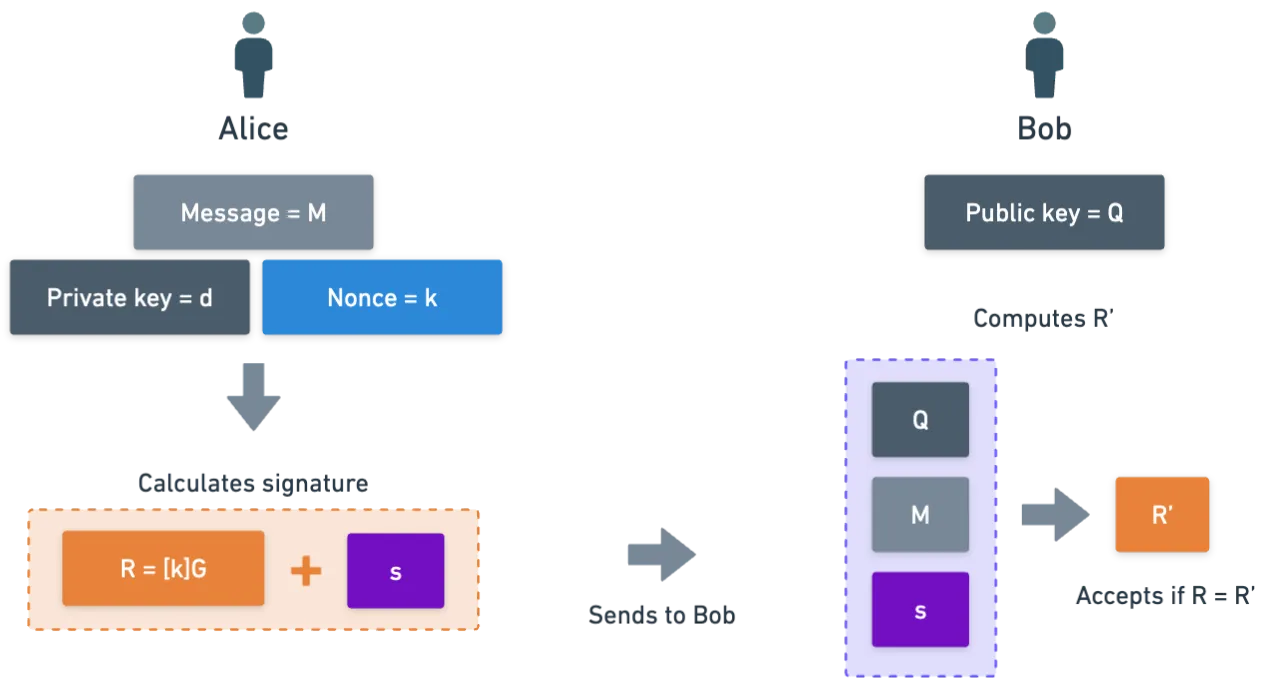
E novamente, como mágica, uma assinatura é realmente apenas um par de números! A ideia aqui é que calcular s é realmente fácil com o conhecimento da chave privada, mas realmente difícil sem ela — você teria que resolver um problema DLP!

Se Charlie quiser mudar a mensagem, ele não tem outra opção além de usar força bruta. E sabemos como isso acaba para ele (spoiler: não vai ser divertido).

Vamos dizer isso novamente, para que fique bem claro:

Assinar envolve calcular uma espécie de "desafio" $R$ e alguma "chave de verificação" $s$. O par $(R, s)$ constitui uma assinatura.

O valor $s$ é especial porque, quando colocado em um liquidificador (ou seja, algum processo) junto com a chave pública $Q$ e a mensagem original $M$, ele produz de volta o desafio $R$. E a ideia é que $s$ só pode ser calculado com o conhecimento da chave privada.

Resumo

Existem várias técnicas e construções mais que exploraremos nos próximos artigos, mas este é um bom lugar para parar por enquanto.

Acredito que não é tão importante entender cada pedaço de matemática ou cada cálculo em jogo, mas apreciar como, no final, tanto a encriptação quanto a assinatura digital realmente equivalem a um uso inteligente de operações de curva elíptica, aproveitando o poder do problema DLP.

A boa notícia é que há muita coisa que podemos fazer com as ferramentas que temos até agora. Técnicas mais sofisticadas exigirão a introdução de alguns conceitos novos e mais complexos — e não vamos chegar lá ainda.

Além disso, há algumas coisas que ainda não explicamos, como transformar uma mensagem em um número, no caso de assinaturas digitais, ou como obter uma máscara a partir de um ponto na curva elíptica, no caso da encriptação.

Isso pode ser feito via hashing, uma ferramenta muito poderosa que será o tema central do próximo artigo!