Criptografia 101: Hashing

Este é parte de uma série de artigos sobre criptografia. Se este é o primeiro artigo que você encontra, eu recomendo começar do início da série.

Da última vez, passamos por algumas técnicas envolvendo grupos de curvas elípticas — especificamente, assinaturas digitais e encriptação assimétrica.

Ambos os métodos foram baseados na premissa de que a mensagem, ou uma máscara da mensagem, eram números inteiros. Mas como isso pode ser? Por exemplo, uma mensagem é muito mais provável de ser alguma string secreta como "string-super-secreta-e-segura", ou mais realisticamente, alguns dados JSON como:

{
  "amount": 1000,
  "account": 8264124135836,
  "transactionReceiptNumber": 13527135
}

Estes claramente não são números inteiros! Assim, eles não são adequados para uso "direto" da maneira que pretendíamos originalmente. Algum tipo de processamento será necessário.

A partir deste ponto, vamos nos desviar um pouco do nosso desenvolvimento de grupos e seus usos. Vamos focar em outra ferramenta que tornará nosso arsenal criptográfico muito mais poderoso.

•••

Funções de Hashing

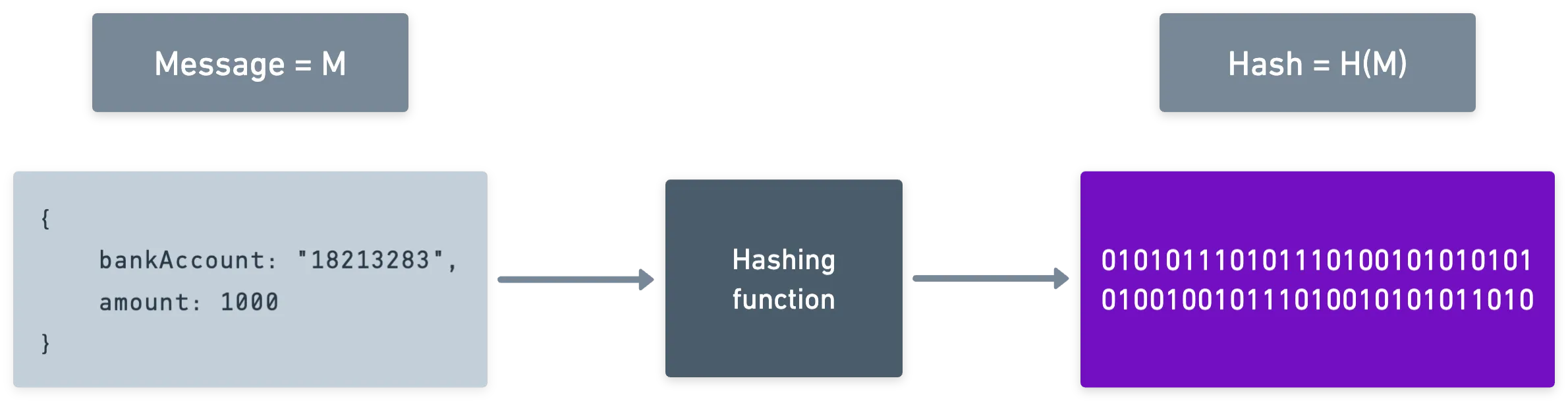
Falando simplesmente, uma função de hashing ou algoritmo de hashing pega alguns dados como entrada e produz informações de aparência aleatória, assim:

Representação de função de hashing pegando qualquer entrada e produzindo uma saída binária de tamanho fixo

A saída geralmente é chamada o hash da entrada. Para nossos propósitos, o algoritmo é como uma caixa preta — ou seja, geralmente não estamos interessados em como o hash é obtido. O que você precisa saber é que funciona essencialmente como um liquidificador de dados: uma vez que os dados entram, eles são embaralhados por toda parte, e você não pode possivelmente recuperar o conteúdo original.

Imagem de um liquidificador — Não sou patrocinado pela Bosch, a propósito. Espero não estar infringindo nenhum direito autoral com isso...

Novamente, não estamos tão interessados em como as funções de hashing conseguem isso. É muito mais importante entender que propriedades o algoritmo e o hash têm, e o que podemos fazer com eles.

Bem, a menos que você esteja tentando desenvolver uma nova função de hashing, é claro. Se é isso que você está procurando, então você OBVIAMENTE se importa com o como. Aqui está um documento do Instituto Nacional de Padrões e Tecnologia (NIST) dos EUA com especificações para diferentes algoritmos de hashing; e aqui também está uma implementação do SHA-256 em Javascript, para referência. Nossa. Boa sorte com isso.

Para propósitos criptográficos, funções de hashing são frequentemente requeridas para ter as seguintes características:

Saída determinística: Dada uma entrada $A$ (como "Eu amo gatos"), a mesma saída é obtida toda vez que fazemos o hash de $A$ .
Difusão: A menor mudança na entrada resulta em uma mudança dramática na saída. Por exemplo, os hashes de "Eu amo gatos" e "Eu amo ratos" são totalmente diferentes, irreconhecíveis um do outro.
Não-previsibilidade: O resultado de fazer hash de alguns dados deve ser totalmente imprevisível; não deve haver padrões reconhecíveis no hash obtido.
Não-reversibilidade: Reconstruir uma entrada válida para um hash dado não deve ser possível, de modo que a única maneira de afirmar que uma entrada corresponde a um hash é através de tentativa e erro (força bruta!).
Resistência a colisões: Encontrar duas entradas que produzem o mesmo hash (ou até mesmo hashes parcialmente correspondentes) deve ser realmente difícil.

Nem todo algoritmo de hashing tem todas essas propriedades. Por exemplo, o algoritmo MD5 não fornece resistência a colisões. Apenas alguns dias atrás, me deparei com este post que mostra uma colisão MD5 de duas strings que diferem em apenas um único bit.

E dependendo da nossa aplicação do algoritmo, isso pode ou não ser importante — por exemplo, MD5 é usado para verificar integridade de arquivos porque é rápido, e não nos preocupamos tanto com colisões nesse contexto.

A saída das funções de hashing tem um tamanho fixo na maioria dos algoritmos. E já que todas as entradas são realmente apenas bits de informação, estamos essencialmente transformando alguma sequência de bits de comprimento arbitrário em uma sequência de bits de tamanho fixo de aparência aleatória. Isso é denotado:

H: \{0,1\}^* \rightarrow \{0,1\}^n

Existem muitos algoritmos de hashing bem conhecidos por aí, como o MD5 mencionado anteriormente, as famílias SHA-2 e SHA-3, o algoritmo de hashing do Ethereum Keccak256, Blake2, que é usado no Polkadot, e outros.

Para Que São Usados os Hashes?

Existem muitas aplicações para hashes. Veremos que eles são úteis para construir protocolos criptográficos, mas existem outros cenários onde o hashing é útil. A lista abaixo é meramente ilustrativa; tenha em mente que hashing é uma ferramenta tremendamente poderosa com aplicação generalizada.

Verificações de integridade de dados: como mencionado anteriormente, uma função de hashing pode ser usada para resumir um arquivo grande em um pequeno pedaço de informação. Até mesmo a menor mudança no arquivo original faz com que o hash mude drasticamente — então pode ser usado para verificar que um arquivo não foi alterado.
Indexação baseada em conteúdo: podemos gerar um identificador para algum conteúdo, usando uma função de hashing. Se a função é resistente a colisões, então o identificador é muito provavelmente único, e poderia até mesmo ser usado em aplicações de banco de dados como um índice.
Estruturas de dados baseadas em hash: algumas estruturas de dados dependem do poder dos hashes. Por exemplo, uma lista hash pode usar o hash do elemento anterior como um ponteiro — muito similar ao que acontece em uma Blockchain. Existem outras estruturas de dados importantes baseadas em hash, como tabelas hash. Vamos dar uma olhada em uma dessas estruturas mais tarde neste artigo.
Esquemas de compromisso: algumas situações requerem que informações não sejam reveladas antes da hora. Imagine que eu quero jogar pedra-papel-tesoura por correspondência. Se eu enviar "pedra" para meu oponente, eles podem simplesmente responder "papel" e ganhar. Mas e se enviássemos um hash de "pedra" ao invés disso? Vamos explorar isso mais a fundo no próximo artigo, mas funções hash são úteis nessas situações.

Certo, agora sabemos o que são funções de hashing, e cobrimos algumas de suas aplicações. Vamos voltar à criptografia baseada em grupos e discutir a importância dos hashes nesse contexto.

•••

Hashes ao Resgate

No início deste artigo, notamos que tanto encriptação quanto assinatura requerem algum tipo de processamento. Na encriptação, precisávamos processar uma máscara, e na assinatura digital, uma mensagem. E em ambos os cenários, precisávamos que a saída fosse algum valor inteiro. As funções de hashing podem nos ajudar nesse esforço?

Lembre-se de que uma função de hashing produzirá uma sequência de bits de tamanho fixo... E o que é isso, senão uma representação binária de um número inteiro?

(10010100010111100)_2 = (75964)_{10}

Mesmo número, expresso em bases diferentes.

Assim mesmo, hashing fornece uma solução para nosso problema: tudo que precisamos é passar nossa mensagem $M$ através de uma função de hashing adequada. A saída, $H(M)$ , será um número, exatamente como precisávamos. Coisa incrível. As coisas estão começando a se encaixar!

Obtendo Pontos de Curvas Elípticas

Ao executar uma função de hashing, a saída será em geral um número binário — outra maneira de dizer isso é que fazemos hash para um número inteiro. Existem situações onde isso não é suficiente, porém: podemos precisar fazer hash para um ponto em uma curva elíptica. Na verdade, seremos obrigados a fazer isso no próximo artigo.

Uma maneira possível de fazer hash para uma curva elíptica é calcular $h = H(M)$ normalmente, e computar um ponto $[h]G$ como nossa saída, com $G$ sendo um gerador da curva elíptica. Métodos mais sofisticados existem, mas não vamos nos aprofundar em mais detalhes. O ponto é que podemos expandir a definição do que é uma função hash, permitindo que ela faça hash para algum conjunto arbitrário $A$ , assim:

H: \{0,1\}^* \rightarrow A

Novamente, a maneira pela qual isso é alcançado é irrelevante para nós, e estamos principalmente preocupados com que propriedades o algoritmo tem — é resistente a colisões? É irreversível?

•••

O Elo Mais Fraco

Vamos voltar ao esquema de assinatura digital (ECDSA) do artigo anterior. Agora sabemos que a mensagem $M$ pode ser processada em um número através do uso de uma função hash, $H(M)$ .

Também dissemos que a segurança da assinatura digital reside em quão difícil é calcular a "chave" de validação $s$ . Mas hashing introduz um novo problema. E explicaremos por meio de um exemplo.

Carlos quer adulterar a mensagem original $M$ . Evidentemente, mudar a mensagem mudará o hash $H(M)$ , e isso torna a assinatura inválida.

No entanto, se $H$ por acaso for uma função de hashing onde é fácil encontrar colisões, então Carlos poderia produzir uma nova mensagem $M'$ mudando a conta bancária para a dele, e então brincar com o valor até que o hash da nova mensagem coincida com o original, $H(M') = H(M)$ .

E boom! Assim mesmo, Carlos enganou nossa segurança. Nesta aplicação particular, uma função de hashing não-resistente a colisões quebraria o algoritmo completamente.

Primeiro, este é um exemplo claro de que nem toda função de hashing é adequada para toda aplicação. E segundo, a segurança de qualquer esquema ou protocolo que possamos pensar será limitada por sua parte mais fraca. Existe um provérbio sábio que diz "uma corrente não é mais forte que seu elo mais fraco". E isso certamente se aplica aqui.

Então sim, é importante ter essas coisas em mente ao projetar técnicas criptográficas. Você deve sempre analisar a segurança de cada componente do seu protocolo, e não apenas focar em um aspecto dele.

Se você quer mais insights sobre assuntos relacionados à segurança, tente ler este texto na série.

•••

Árvores de Merkle

Antes de concluir, quero falar sobre uma importante estrutura de dados baseada em hash, que é essencial no desenvolvimento de Blockchain: árvores de Merkle.

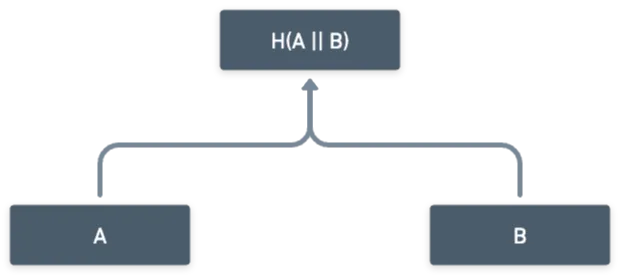
Em essência, é apenas uma estrutura de árvore onde a informação contida em cada nó é apenas o hash dos nós filhos. Assim:

Construção de nós em árvores de Merkle — Um nó de uma árvore de Merkle

Repetir este padrão levará a uma estrutura de árvore:

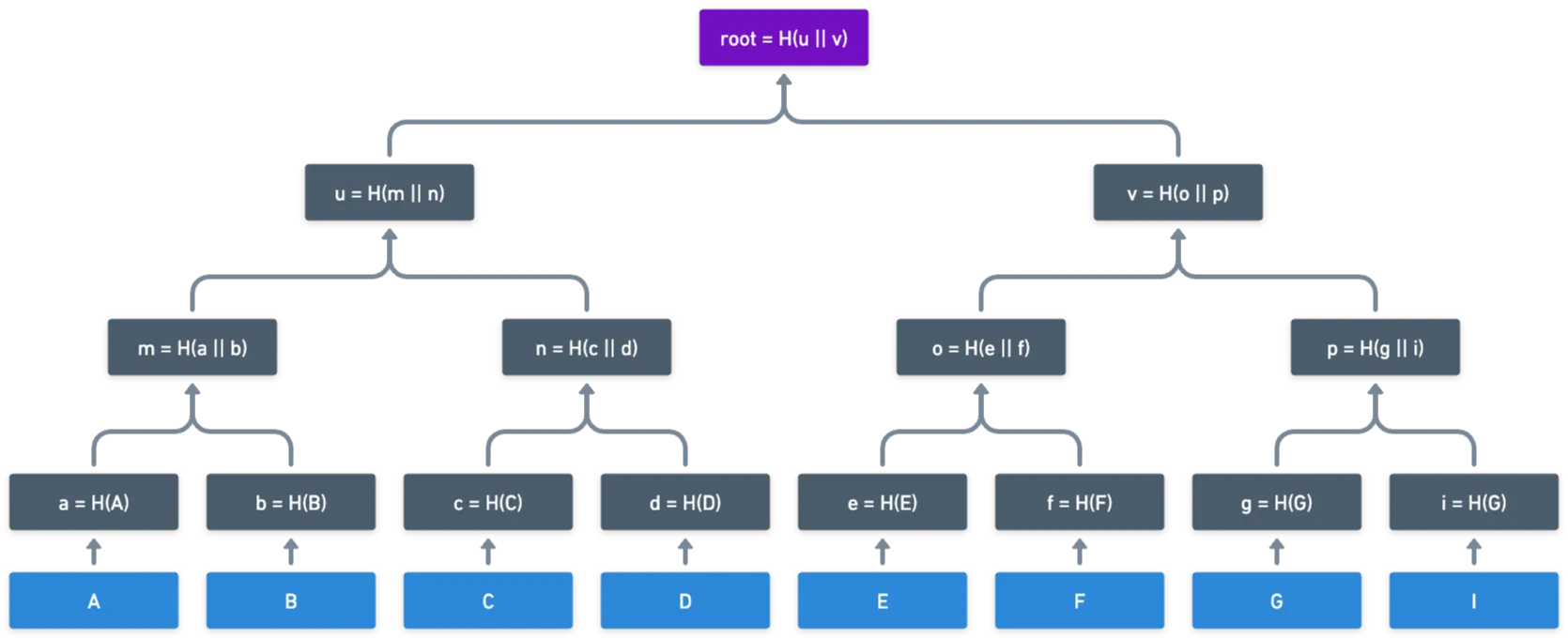
Tudo isso faz é reduzir (possivelmente) muita informação a um único hash, que é a raiz da árvore. Mas espere, uma função hash não faz a mesma coisa? Se simplesmente fizermos hash de:

h = H(A || B || C || D || E || F || G || I)

Também obtemos um único hash associado com a mesma informação. Mudar um único bit em qualquer uma das entradas originais causa mudanças dramáticas no hash produzido. Então... Por que se incomodar em criar uma estrutura de árvore estranha?

A propósito, o operador $||$ significa concatenação de bits. É apenas colar os bits das entradas juntos. Então, por exemplo, se $A = 0101$ e $B = 1100$ , então $A || B = 01011100$ .

Como acontece, usar uma árvore desbloqueia novos superpoderes. Imagine esta situação: alguém (vamos dizer André) afirma que $h$ corresponde à entrada $A$ , mas não quer revelar as outras entradas $(B, C, D...)$ . Como podemos verificar se $A$ efetivamente produz $h$ ?

Nossa única opção é fazer hash de toda a entrada e comparar com $h$ . E é claro, para isso, precisamos de todas as entradas originais usadas por André. Mas ele não quer compartilhar todas as entradas, e enviar uma carregada de informações (possivelmente milhares de valores) através de uma rede não soa muito atrativo...

A Solução da Árvore de Merkle

A estratégia claramente se torna ineficiente. Árvores de Merkle permitem uma solução mais elegante. Imagine que André produziu ao invés disso uma raiz de Merkle $R$ de todas as suas entradas $(A, B, C...)$ :

R = \textrm{Merkle}(A, B, C...)

Ele afirma que $A$ está na árvore. Como ele pode provar isso? E aqui é onde a mágica acontece: ele pode apenas enviar alguns nós da árvore como prova, e podemos verificar que $R$ é de fato produzido com $A$ . Dê uma olhada nesta imagem:

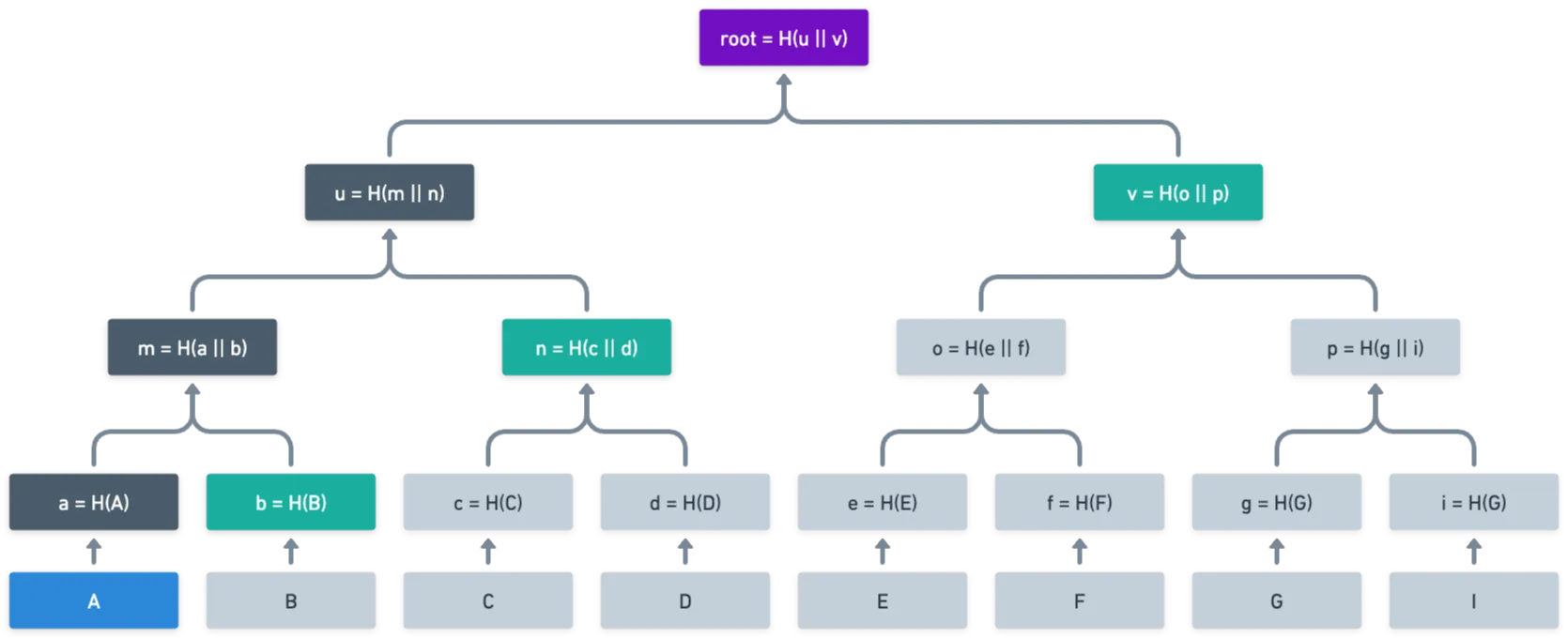
Visualização de prova de Merkle, com apenas alguns nós necessários para a prova

Vê os nós destacados em verde? Essa é toda a informação que realmente precisamos para calcular a raiz. Veja, podemos calcular $m = H(a || b)$ , e então $u = H(m || n)$ , e finalmente $H(u || v)$ , e pronto. Ao invés de revelar todas as folhas da árvore $(A, B, C, D, E, F, G, I)$ , somos capazes de demonstrar que $A$ pertence à árvore revelando apenas três nós!

Este sistema é conhecido como prova de Merkle. E uma coisa muito legal sobre isso é como bem ele escala. Acontece que o número de nós $N$ que temos que revelar escala logaritmicamente com o número de entradas:

N = \textrm{log}_2(\#\textrm{entradas})

Então para 1024 entradas, temos que revelar apenas 10 nós. Para 32768, 15 nós serão suficientes.

Uma imagem de uma foca feliz — Relaxante

Árvores de Merkle são uma das estruturas de dados criptográficas mais usadas por aí, alimentando Blockchains em todos os lugares. Há pesquisa ativa acontecendo para possivelmente substituí-las por um novo garoto no pedaço, chamado árvore de Verkle, mas a ideia é geralmente a mesma: provar que algo pertence a um conjunto de dados, sem revelar o conjunto de dados inteiro.

Isso só mostra como hashes podem ser utilizados de maneiras inteligentes para realizar algumas façanhas bem mágicas!

•••

Resumo

Devagar mas seguro, estamos construindo um conjunto sólido de ferramentas criptográficas. Agora temos hashing à nossa disposição, junto com grupos, aritmética modular e curvas elípticas. Massa!

Depois deste breve desvio do nosso desenvolvimento em curvas elípticas, vamos pular direto de volta para a ação no próximo artigo, e explorar o que mais podemos fazer com nosso conhecimento atual.