Criptografia 101: Assinaturas Turbinadas

Este é parte de uma série de artigos sobre criptografia. Se este é o primeiro artigo que você encontra, eu recomendo começar do início da série.

Se você tem acompanhado a série, então já viu sua boa dose de loucuras criptográficas. Especialmente no artigo anterior. Ainda assim... Isso é apenas a ponta do iceberg.

Há muito mais para aprender. Podemos fazer muito mais com curvas elípticas (e grupos em geral, para ser justo). Em particular, assinaturas digitais têm algumas variantes elegantes que se mostram extremamente úteis no contexto certo. Este será o tópico do artigo de hoje.

Um Aviso Amigável

Acredito que é neste ponto da série onde a matemática fica um pouco mais apimentada que o usual. A complexidade dos protocolos que vão ser apresentados é um pouco maior. Se você está aqui apenas para ter uma ideia geral das técnicas criptográficas, então sugiro ler apenas a introdução de cada tópico. Farei o meu melhor para manter as introduções simples e autocontidas, para que forneçam uma boa ideia geral, sem o incômodo de entender a matemática.

Vamos lá!

Assinaturas Cegas

Em alguns casos, pode ser necessário assinar informações privadas. Por exemplo, em um sistema de votação, um usuário pode querer manter seu voto privado, mas exigir aprovação de algum terceiro. Este último teria que assinar o voto às cegas — sem saber qual é o voto do usuário.

Claro, mesmo que isso seja tecnicamente possível, uma assinatura cega deve ser implementada com cuidado. Você não quer estar assinando às cegas uma transação que vai zerar sua conta!

Ainda assim, quando as assinaturas cegas são necessárias, há muitas maneiras de construí-las. Uma possibilidade é adaptar esquemas de assinatura existentes. Em particular, adaptar assinaturas Schnorr é bastante simples. Vamos tentar isso!

O ponto é que André não sabe o que está assinando — ele vai ser solicitado por Bruna a assinar alguma mensagem $M$ que ela previamente cega ou mascara. E depois de criar a assinatura, Bruna tem uma maneira de desmascarar, para que a verificação funcione com sua mensagem original.

Click to zoom

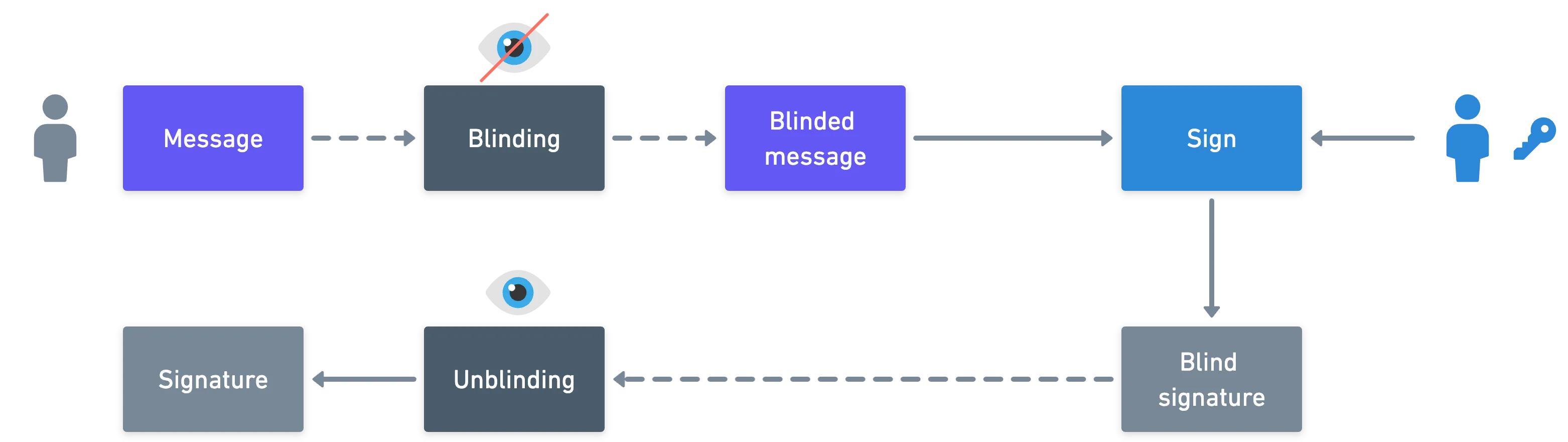
Em resumo:

As assinaturas cegas permitem a assinatura de informações privadas

O Protocolo

Começamos como de costume: André tem chave privada $d$ e chave pública $Q = [d]G$. Ele será nosso assinante. Como sempre, $G$ é um gerador para o grupo de curva elíptica escolhido, e tem ordem $n$.

O processo começa com André escolhendo um inteiro aleatório $k$, e calculando $R = [k]G$. Ele envia isso para Bruna, e então ela inicia o procedimento de cegamento:

• Bruna escolhe um inteiro aleatório $b$, que é chamado de fator de cegamento,
• Ela então calcula:

$$R' = R + [b]Q$$

• E usa isso para calcular um desafio:

$$e' = H(M || R')$$

• Finalmente, ela também cega o desafio:

$$e = e' + b \ \textrm{mod} \ n$$

Tudo que resta é André assinar. Ele recebe $e$, e simplesmente calcula a assinatura como de costume:

$$s = k + e.d \ \textrm{mod} \ n$$

Neste exemplo particular, Bruna não precisa fazer nada ao receber a assinatura — a saída é simplesmente $(s, e')$. Mas em geral, é possível que ela precise reverter o processo de cegamento em outras versões de assinaturas cegas.

A verificação acontece exatamente como no caso padrão de assinatura Schnorr:

$$V = [s]G - [e']Q$$

Se isso for igual a $R'$, então $H(M || V)$ será exatamente igual ao desafio $e'$, e a assinatura é aceita. E este deveria ser o caso, porque:

$$V = [e.d + k]G - [e'.d]G = [(e' + b)d - e'.d + k]G$$ $$= [e'.d - e'.d + k + b.d]G = [k]G + [d.b]G = [k]G + [b]Q = R'$$

Como um relógio suíço, vemos que um $s$ corretamente calculado deveria de fato verificar a assinatura (porque recuperamos o desafio original).

A propósito, estou propositalmente omitindo as operações módulo $n$, por simplicidade. Mas para tratamento rigoroso, elas deveriam ser incluídas na demonstração.

Assinatura cega, check. Não é tão louco, né?

Agora que aquecemos, vamos subir o nível...

Assinaturas em Anel

Toda vez que você assina digitalmente algo, a verificação acontece com conhecimento de sua chave pública. Portanto, você não tem anonimato: sua chave pública o identifica como um indivíduo portador de uma chave privada. Mas, você acreditaria se eu te dissesse que há uma maneira de assinar coisas anonimamente?

As assinaturas em anel oferecem tal funcionalidade. A premissa é que uma única pessoa em um grupo de pessoas gera uma assinatura que não revela quem no grupo foi o assinante original. Algo assim:

Click to zoom

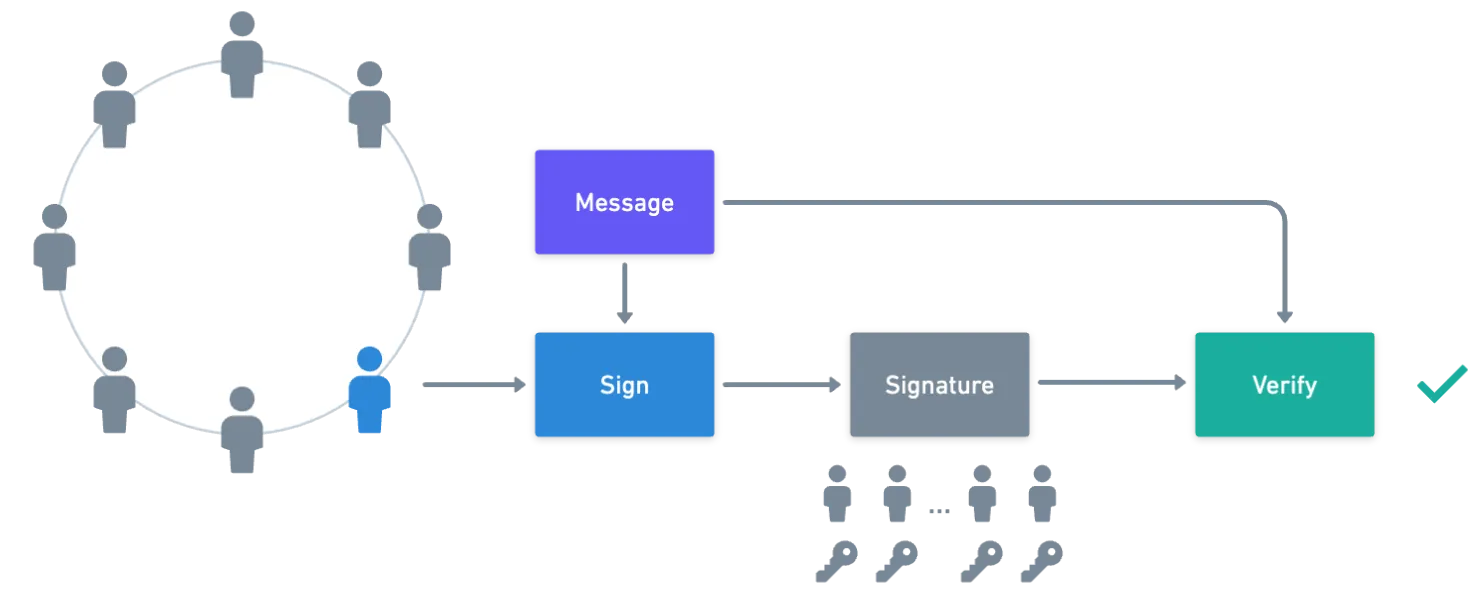
Novamente, como um breve resumo preliminar:

As assinaturas em anel permitem que um usuário em um grupo crie uma assinatura que poderia ter sido produzida por qualquer membro do grupo, preservando assim o anonimato do usuário

Criando o Anel

Para conseguir esse comportamento de anonimato, primeiro devemos forjar uma estrutura nova e um pouco incomum, chamada anel.

O conceito de um anel é o de um conjunto ordenado (neste caso, de participantes), e cuja ordem determina uma série de cálculos começando de um valor $A$, e terminando no mesmo valor $A$. E como sempre, a ideia é que criar essa sequência de computações só é viável com conhecimento de uma chave privada.

A propósito, este não é um anel como na estrutura algébrica abstrata. Falaremos sobre esses mais tarde.

Então, para a configuração: o anel tem $p$ participantes, que como mencionado anteriormente, são ordenados. Isto é, André é o participante $\#1$, Bruna é a participante $\#2$, e assim por diante.

Sara, que é a participante $\#s$, tem conhecimento das chaves públicas de todos os outros participantes — vamos denotar essas como $Q_i$. Ela também tem seu próprio par de chaves privada e pública, que serão $d_s$ e $Q_s = [d_s]G$.

Para produzir uma assinatura para uma mensagem $M$, Sara faz o seguinte:

• Ela escolhe um inteiro aleatório $k$, e calcula $R = [k]G$.
• Ela então calcula uma semente, $v = H(M || R)$.

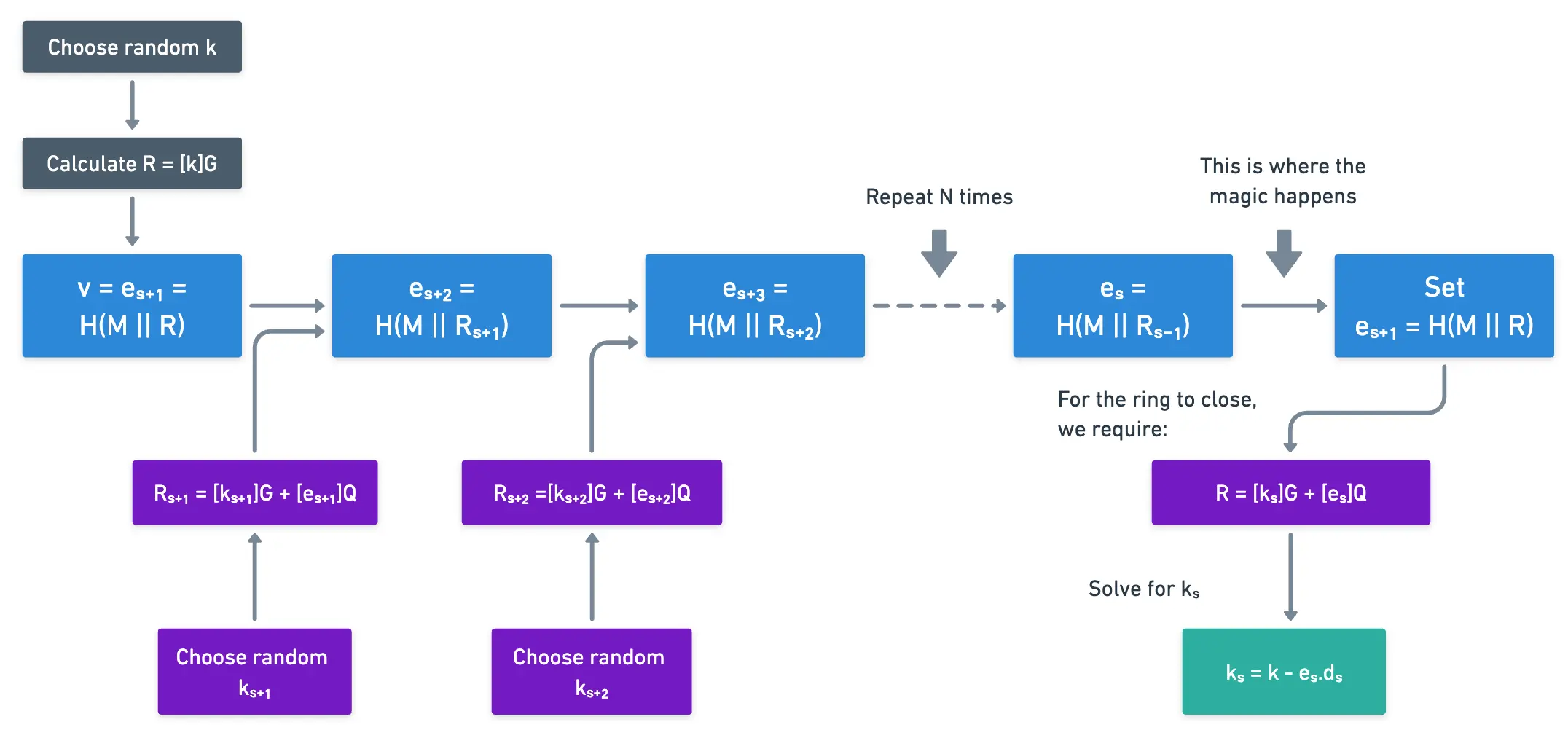
Esta semente será usada para um processo iterativo. Ela começa definindo $e_{s+1} = v$, e então para cada outro dos $p$ participantes no anel:

• Ela escolhe um valor aleatório $k_i$, e calcula:

$$R_i = [k_i]G + [e_i]Q$$

• E calcula o próximo desafio:

$$e_{i+1} = H(M || R_i)$$

Eventualmente, Sara faz isso para todos os participantes, obtendo um desafio final, que chamaremos apenas de $e$. Ela faz isso em ordem, começando por ela mesma (s), e então calculando $e_{s+1}$. Ela continua com este processo, e ao chegar ao participante $p$, então ela conta de $1$ até $s$. Isso é crucial, porque a assinatura será avaliada exatamente nesta mesma ordem.

$$e_{s+1} \rightarrow e_{s+2} \rightarrow ... \rightarrow e_p \rightarrow e_1 \rightarrow ... \rightarrow e_{s-1} \rightarrow e_s$$

Tudo que resta é ela fechar o anel, significando que a computação final deveria retornar o valor inicial, então $e_{s+1} = v$. Para isso, ela tem que encontrar algum valor $k_s$ tal que:

$$R_s = [k_s]G + [e_s]Q$$ $$e_{s+1} = H(M || R_s)$$

Como sabemos que $e_{s+1} = v = H(M || R)$, tudo que precisamos é encontrar um valor de $k_s$ tal que $R = R_s$. Reorganizando um pouco:

$$R = R_s \Rightarrow [k]G = [k_s]G + [e_s]Q$$ $$\mathcal{O} = [k_s]G + [e_s.d_s]G - [k]G = [k_s + e_s.d_s - k]G$$ $$k_s = k - e_s.d_s$$

Podemos obter o valor desejado para $k_s$. A assinatura final é a tupla:

$$(e_1, k_1, k_2, ..., k_p)$$

É importante que os valores sejam fornecidos na ordem do anel. Sara estará em algum lugar no meio, escondida...

Aqui está uma representação visual de todo o processo de assinatura, para ajudar a entender melhor todos os passos envolvidos:

Click to zoom

Verificação

Tudo que resta é verificar a assinatura. Para isso, Bruna começa de $e_1$, e calcula o seguinte para cada participante $i$:

• O valor $R_i = [k_i]G + [e_i]Q_i$
• E o próximo desafio, como:

$$e_{i+1} = H(M || R_i)$$

Se o loop se fecha corretamente, significando que o desafio final produz exatamente $e_1$, então ela aceita a assinatura. Note que o anel se fecha porque nos asseguramos de encontrar um $k_{s-1}$ adequado para Sara! E fizemos isso usando a chave privada de Sara — se não a conhecêssemos, então encontrar o $k_{s-1}$ certo não é uma tarefa fácil.

Do ponto de vista do verificador, todos os valores $k$ são indistinguíveis uns dos outros (são apenas números), então ela não pode saber qual é o calculado — lembre-se que os outros são apenas aleatórios!

Tudo bem, isso foi certamente muito!

Aviso: somatórias pela frente. Respire fundo. Hidrate-se. Pause por um minuto.

Pronto? Vamos continuar.

Multiassinaturas

A ideia é simples: o que acontece se precisássemos de múltiplos participantes para assinar algo? E isso não é tão absurdo: é frequentemente um requisito ao assinar documentos legais do mundo físico. Parece uma extensão muito natural.

Multiassinaturas são especialmente úteis ao assinar operações sensíveis. Por exemplo, ações administrativas em uma aplicação podem exigir uma assinatura de múltiplos membros de uma organização. Isso garante que nenhum ator único tenha privilégios administrativos, e que não existe um único ponto de falha.

Click to zoom

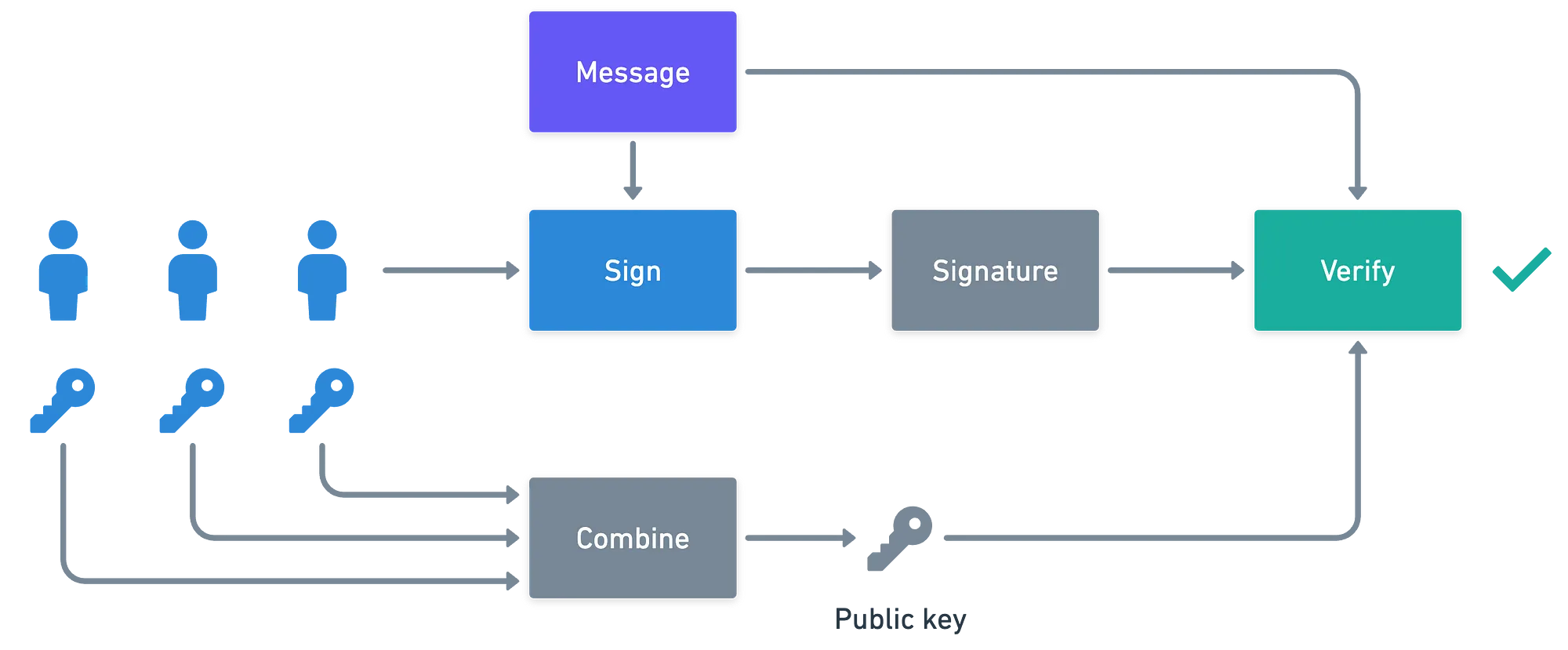
Seguindo o padrão dos exemplos anteriores, vamos dar um breve resumo antes de mergulhar na matemática:

As multiassinaturas permitem que múltiplos usuários assinem uma única mensagem, de modo que a assinatura não é válida se não foi assinada por usuários suficientes

Há múltiplas maneiras de fazer isso.

Multiassinaturas Schnorr

Assinaturas Schnorr têm uma propriedade muito boa: elas são lineares. Simplificando, isso significa que podemos somar assinaturas individuais e ainda acabar com uma assinatura válida. Não há inversos multiplicativos complicados na mistura que poderiam potencialmente complicar as coisas.

Por causa disso, podemos adaptar o esquema que já apresentamos, para que múltiplos participantes possam assinar uma mensagem.

A configuração é ligeiramente diferente do usual: cada um dos $p$ participantes tem uma chave privada $d_i$, e tem uma chave pública como $Q_i = [d_i]G$. Também precisaremos de uma chave pública combinada $Q$, calculada como:

$$Q = \sum_{i=1}^p Q_i$$

Note que este é exatamente o mesmo resultado como se tivéssemos somado as chaves privadas primeiro, e então calculado $Q$:

$$\left [ \sum_{i=1}^p d_i \right ]G = \sum_{i=1}^p [d_i]G = \sum_{i=1}^p Q_i$$

Depois, a assinatura acontece da seguinte forma:

• Cada participante escolhe um número aleatório $k_i$, e calcula $R_i = [k_i]G$.
• Então, os $R_i$ individuais são combinados assim:

$$R = \sum_{i=1}^p R_i$$

• Com isso, um desafio $e$ é calculado como $e = H(R || M)$.
• Então, cada participante calcula uma assinatura individual $s_i$:

$$s_i = k_i - e.d_i \ \textrm{mod} \ n$$

• Finalmente, as assinaturas parciais são somadas para produzir um único $s$, como:

$$s = \sum_{i=1}^p s_i \ \textrm{mod} \ n$$

E como antes, a assinatura produzida é o par $(e, s)$. Curiosamente, este par é verificado exatamente como uma assinatura Schnorr normal! O verificador calcula $R' = [s]G + [e]Q$, e aceita se $e = H(R' || M)$. É aqui que a linearidade entra: podemos mostrar que $R'$ deveria ser igual a $R$, e assim a assinatura deveria funcionar.

$$R' = [s]G + [e]Q = \left [ \sum_{i=1}^p s_i + e.\sum_{i=1}^p d_i \right ]G = \left [ \sum_{i=1}^p k_i + e.d_i - e.d_i \right ]G$$ $$R' = \left [ \sum_{i=1}^p k_i \right ]G = \sum_{i=1}^p [k_i]G = \sum_{i=1}^p R_i = R$$

Lembre-se que estou propositalmente omitindo as operações módulo $n$ para manter as coisas o mais simples e limpas possível. Tratamento rigoroso requer que você leve a operação em conta!

E assim, múltiplos participantes produziram uma única assinatura! Legal!

Assinaturas de Limite

Assinaturas de limite oferecem uma funcionalidade ligeiramente mais avançada. O termo limiar alude ao fato de que um certo número mínimo de assinantes será necessário para que a assinatura seja válida. Precisamos de $t$ participantes de um grupo de $m$ pessoas para se engajarem na assinatura, para produzir uma assinatura.

Como sempre, vamos precisar de uma chave privada. Mas como antes, o ponto é que nenhum ator único a conhece — eles apenas possuem partes ou pedaços dela. Conseguir isso no caso de assinaturas de limiar não é trivial — não dá pra simplesmente escolher um inteiro aleatório, como era o caso para outros esquemas.

De fato, geração de chaves é um passo crucial para assinaturas de limiar funcionarem.

Honestamente, entender assinaturas de limiar envolve usar polinômios, que ainda não cobrimos. Eles serão o tópico central em próximas partes. Por enquanto, devemos nos contentar em saber sobre a existência deste tipo de assinaturas. Voltaremos a elas mais tarde na série.

Resumo

As assinaturas vêm em muitas formas diferentes. No final, é tudo sobre criar um jogo criptográfico que tem propriedades específicas. Qualquer necessidade que você possa ter, provavelmente consegue criar uma estratégia que a cubra.

Você precisa de assinatura anônima mas com um admin que pode revogar assinaturas? As assinaturas de grupo estão aí para salvar o dia. Quer alterar a mensagem, mas manter uma assinatura válida? Aa assinaturas homomórficas são a sua praia.

Agora vimos um número significativo de aplicações criptográficas baseadas em grupos. É hora de aprofundarmos nosso entendimento de grupos um passo adiante — então da próxima vez, veremos homomorfismos e isomorfismos de grupos. E por sua vez, cobriremos uma nova técnica criptográfica útil.