Criptografia 101: Homomorfismos e Isomorfismos

Este é parte de uma série de artigos sobre criptografia. Se este é o primeiro artigo que você encontra, eu recomendo começar do início da série.

Até agora, nossa compreensão básica de grupos tem se mostrado útil o suficiente para projetar esquemas criptográficos que se adaptam a muitas necessidades — encriptação, assinaturas, (e algumas variantes exóticas), provas, compromissos, aleatoriedade verificável, etc.

Acredito que é o momento certo para aprofundar um pouco mais nossa compreensão das estruturas de grupo e, ao fazer isso, descobrir um novo conjunto de primitivos criptográficos incríveis.

É possível que você já tenha ouvido falar de homomorfismos e isomorfismos. Mas o que são essas coisas com nomes tão peculiares?

Homomorfismos em Poucas Palavras

Em geral, um homomorfismo é uma função ou mapeamento que preserva propriedades algébricas.

Lembre-se de que quando trabalhamos com grupos, temos apenas um conjunto e uma operação. Então um homomorfismo de grupo realmente mapeia elementos de um grupo para outro grupo, onde as propriedades da operação são preservadas.

Todo esse trava-línguas pode ser reduzido a isto: se a e b são elementos de um grupo, então um homomorfismo f deveria se comportar assim:

$$f(a + b) = f(a) + f(b)$$

Um grande exemplo de homomorfismo ocorre quando pegamos um grupo de curva elíptica com gerador $G$ e ordem $n$, e o grupo aditivo de inteiros módulo $n$. E simplesmente definimos:

$$f: \mathbb{Z}_n \rightarrow \langle G \rangle \ / \ f(x) = [x]G$$

Podemos ver facilmente que a adição é preservada:

$$f(a) + f(b) = [a]G + [b]G = [a + b]G = f(a + b)$$

Isomorfismos

Note que no caso acima, há uma correspondência um para um entre os elementos de ambos os grupos. Isso não precisa ser sempre o caso: se tivéssemos escolhido os inteiros módulo $q$, com $q > n$, então pelo menos dois inteiros compartilhariam o mesmo valor funcional.

No caso de existir uma correspondência um para um, então em teoria poderíamos usar $f$ para mapear $\mathbb{Z}_n$ para $\langle G \rangle$, e sua inversa $f^{-1}$ para mapear $\langle G \rangle$ para $\mathbb{Z}_n$.

Em termos matemáticos, isso significa que f é uma bijeção. Você sabe, caso você queira ser mais preciso sobre isso!

Quando isso acontece, dizemos que $f$ é um isomorfismo em vez de um homomorfismo. E diz-se que os grupos são isomórficos.

Para o que nos importa em termos de teoria de grupos, grupos isomórficos são essencialmente o mesmo grupo disfarçado, já que podemos encontrar uma função que nos permita transformar um grupo no outro, e vice-versa.

Por Que Eu Deveria Me Importar?

Ah, a pergunta de um milhão de dólares.

A ideia de que grupos sejam homomórficos ou isomórficos é muito interessante, porque se movimentar de um lado para outro entre os grupos escolhidos significa que podemos realizar operações em qualquer um deles. E isso nos permite fazer um pouco de mágica. Veremos isso em ação em um minuto.

Antes de pular para um exemplo, quero esclarecer algumas notações que você pode encontrar. Se você conferir, por exemplo, esta página sobre o criptossistema ElGamal (um algoritmo que veremos em um momento), notará que eles não parecem usar adição ao trabalhar com grupos. Em vez disso, usam multiplicação e notação exponencial:

$$y = g^x$$

Hmm. Isso não se parece com nossos exemplos anteriores. Como é isso?

A chave para entender isso é ver as coisas através da lente do isomorfismo. Dê uma olhada nestes dois grupos:

$$\mathbb{Z}_5 = \{0, 1, 2, 3, 4\}$$ $$G_5 = \{1, g, g^2, g^3, g^4\}$$

Se simplesmente pegarmos papel e caneta e combinarmos elemento por elemento, podemos ver claramente que há uma correspondência um para um. Formalmente, a relação tem a forma:

$$f(x) = g^x$$

Dizemos que o segundo grupo é multiplicativo — note que a soma de elementos em $\mathbb{Z}_5$ é substituída pela multiplicação de elementos em $G_5$:

$$f(a + b) = g^{a+b} = g^a.g^b = f(a).f(b)$$

Isso é totalmente aceitável, já que as operações em ambos os grupos não são necessariamente as mesmas.

Então sim, se você alguma vez vir a notação multiplicativa enquanto olha um sistema baseado em grupos, tenha em mente que provavelmente também pode ser formulada uma versão aditiva através deste isomorfismo.

Encriptação Homomórfica

Certo, chega de formalismos. Vamos para a parte boa.

Suponha que você queira realizar uma soma de dois inteiros, módulo $q$. Mas estes números estão encriptados ou cifrados. Normalmente, você teria que decriptar ambos os números e somá-los. E se você quiser armazenar o resultado encriptado, teria que encriptar novamente.

Mas e se pudéssemos pular a decriptação completamente?

Este é exatamente o objetivo da encriptação homomórfica: realizar operações com dados protegidos e privados, mas obter o mesmo resultado como se operássemos com os dados em texto simples e desprotegidos, e então os encriptássemos.

Click to zoom

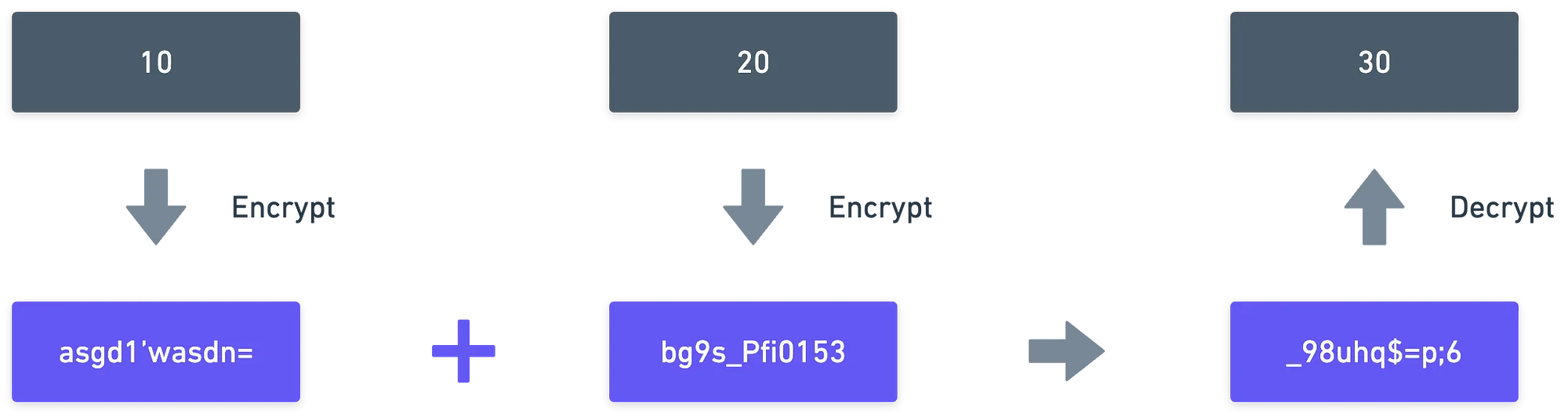
E isso é incrível, porque podemos economizar o tempo de executar operações de decriptação — que são caras —, enquanto preservamos a privacidade dos dados.

Em teoria, pelo menos. Há algumas nuances em torno disso, como discutiremos em um minuto. Mas a parte da privacidade é incrível, isso sim!

Então, como conseguimos esse tipo de funcionalidade?

Cifra ElGamal

Este é um dos criptossistemas mais simples que existem. Apesar de sua simplicidade, a função de cifra ou encriptação tem uma propriedade muito legal: é homomórfica!

Portanto, podemos realizar operações com os dados cifrados. Vamos ver como funciona.

Como sempre, começaremos com André tendo uma chave privada $d$, que ele usa para calcular uma chave pública $Q = [d]G$. E sim, $G$ é seu típico gerador de curva elíptica.

Digamos que Bruna quer cifrar uma mensagem para André, conhecendo sua chave pública $Q$. Para que isso funcione, devemos assumir que a mensagem é um ponto na curva elíptica, $M$. E isso pode ser obtido passando a mensagem original através de uma função reversível (o hashing não vai servir).

Não vamos cobrir como fazer esse primeiro passo agora — vamos apenas assumir que sabemos como fazer isso.

Então, Bruna segue este procedimento para cifrar:

• Escolhe um inteiro aleatório r, e calcula $R = [r]G$.
• Depois, calcula uma máscara (como sempre) como $[r]Q$.
• Finalmente, adiciona a máscara à mensagem, assim $C = M + [r]Q$.

O texto cifrado obtido é $(R, C)$. Para decriptar, André tem que:

• Calcular $[d]R$, que será exatamente igual à máscara $[r]Q$.
• Subtrair a máscara de $C$, assim $C - [r]Q = M$.

Já que estamos sendo mais precisos agora, podemos dizer que subtrair é realmente adicionar o inverso aditivo do valor subtraído. É só mais fácil dizer "subtrair".

A parte de cifra deste processo pode ser expressa como uma função que pega uma mensagem $M$ e alguma aleatoriedade $r$, e produz um texto cifrado:

$$\varepsilon: \langle G \rangle \times \mathbb{Z}_q \rightarrow \langle G \rangle \times \langle G \rangle \ / \ \varepsilon(M,r) = ([r]G, M + [r]Q)$$

E este será nosso homomorfismo.

Imagine que você cifra $M_1$ com aleatoriedade $r_1$, e $M_2$ com aleatoriedade $r_2$. O que acontece se somarmos os resultados cifrados?

$$\varepsilon(M_1, r_1) + \varepsilon(M_2, r_2) = ([r_1]G, M_1+[r_1]Q) + ([r_2]G, M_2+[r_2]Q)$$ $$= ([r_1 + r_2]G, M_1+M_2+[r_1 + r_2]Q) = \varepsilon(M_1 + M_2, r_1 + r_2)$$

E boom! O resultado é o mesmo como se tivéssemos somado primeiro as mensagens (e a aleatoriedade)!

Como num passe de mágica.

Observações

O esquema apresentado acima é tão simples quanto pode ser. E embora este exemplo seja muito ilustrativo, não é perfeito de forma alguma, e há uma ou duas coisas que devemos dizer sobre ele.

Mensagens Codificáveis

Primeiro, note que a mensagem que podemos encriptar está relacionada à ordem do grupo, $n$. Lembre-se de que a ordem do grupo significa o número de elementos no grupo, então há apenas um número finito (exatamente $n$) de pontos diferentes no grupo.

Como é necessário codificar reversivelmente nossa mensagem para um ponto $M$, então isso significa que cada ponto $M$ corresponde a uma mensagem única, então há apenas $n$ mensagens únicas que podemos codificar.

E isso, por sua vez, significa que não podemos codificar uma mensagem de comprimento arbitrário. Poderíamos pensar em estratégias engenhosas para dividir uma mensagem em "pedaços", mas isso poderia minar o aspecto homomórfico do nosso esquema.

Mas isso não significa que a técnica não tenha valor — por exemplo, pense nas mensagens como saldos privados. Poderíamos lidar com um saldo máximo representável, né?

Homomorfismo Parcial

Por outro lado, esta cifra homomórfica suporta apenas uma operação. E isso é esperado, já que estamos trabalhando com grupos. Então se a operação do grupo é a soma, então não podemos fazer multiplicação. E portanto, isso é conhecido como Cifra Parcialmente Homomórfica, ou PHE (por suas siglas em inglês).

Se pudéssemos suportar tanto a soma quanto a multiplicação, então nosso esquema seria completamente homomórfico — e falaríamos de Encriptação Completamente Homomórfica, ou FHE (Fully Homomorphic Encryption) por suas siglas em inglês.

Criar um esquema de cifra completamente homomórfico não é tarefa fácil — e grupos simplesmente não vão dar conta. Precisaremos de uma estrutura matemática diferente para abordar isso, uma que suporte duas operações. Quando esse é nosso requisito, precisamos entrar no domínio da teoria de anéis, um esforço que empreenderemos mais tarde na série.

Provas de Conhecimento Zero

Imagine uma aplicação com saldos privados. Você pode decriptar seu próprio saldo, mas quem processa uma solicitação de transferência não pode. Portanto, você precisa provar de alguma forma para o processador que:

• Conhece seu saldo e a quantia a transferir
• Tem saldo suficiente para cobrir a transferência

Mas você precisa fazer isso sem revelar os valores, porque o objetivo principal da aplicação é manter os saldos privados!

Para fazer isso, precisaremos combinar nossos esforços de cifra homomórfica com Provas de Conhecimento Zero (ZKPs por suas siglas em inglês). E geralmente falando, as ZKPs tendem a ser computacionalmente caras — então os benefícios de não ter que decriptar são de alguma forma equilibrados por isso. No entanto, a privacidade dos dados pode ser necessária — por exemplo, a encriptação homomórfica é uma solução atraente para privacidade em redes públicas, como Blockchains.

Resumo

Desta vez, nos aprofundamos um pouco mais na matemática, o que em última análise nos permite entender melhor as estruturas que sustentam nossas construções.

Vimos um esquema de encriptação (parcialmente) homomórfico em ação. Claro, o ElGamal não é o único sistema que tem essa propriedade de homomorfismo. Existem outros esquemas baseados em grupos, como o criptossistema Benaloh ou o muito citado criptossistema Paillier.

Percorremos um longo caminho. Por enquanto, vamos encerrar nossa exploração da criptografia de curvas elípticas (ECC). Mas este não é o fim da jornada, de forma alguma. Acontece que grupos de curvas elípticas funcionam muito bem com outra construção que permite criptografia muito interessante. Entraremos nisso em breve.

No entanto, há um tópico que quero abordar antes: polinômios e as possibilidades que eles oferecem. Este será o tópico do próximo artigo!