Criptografia 101: Emparelhamentos

---

Este é parte de uma série de artigos sobre criptografia. Se este é o primeiro artigo que você encontra, eu recomendo começar do início da série.

Já exploramos várias aplicações para curvas elípticas — alguns esquemas simples e alguns mais avançados. Também jogamos polinômios na mistura ao estudar Assinaturas de Limite. Se esticarmos os limites da criatividade, ainda podemos criar muitos protocolos baseados apenas nessas construções.

Mas isso não significa que não existam outras ferramentas por aí. E há uma muito importante que ainda precisamos apresentar: emparelhamentos (pairings).

Neste artigo, vamos definir o que eles são — mas não como computá-los. A razão para isso é que ainda não definimos a maquinaria matemática necessária para o cálculo de emparelhamentos. Isso, podemos explorar mais tarde, mas se você está interessado, este é um excelente recurso para olhar enquanto isso. E também existem muitas bibliotecas por aí que cobrem o cálculo de emparelhamentos se você quiser começar a brincar com eles depois de ler este artigo!

Emparelhamentos

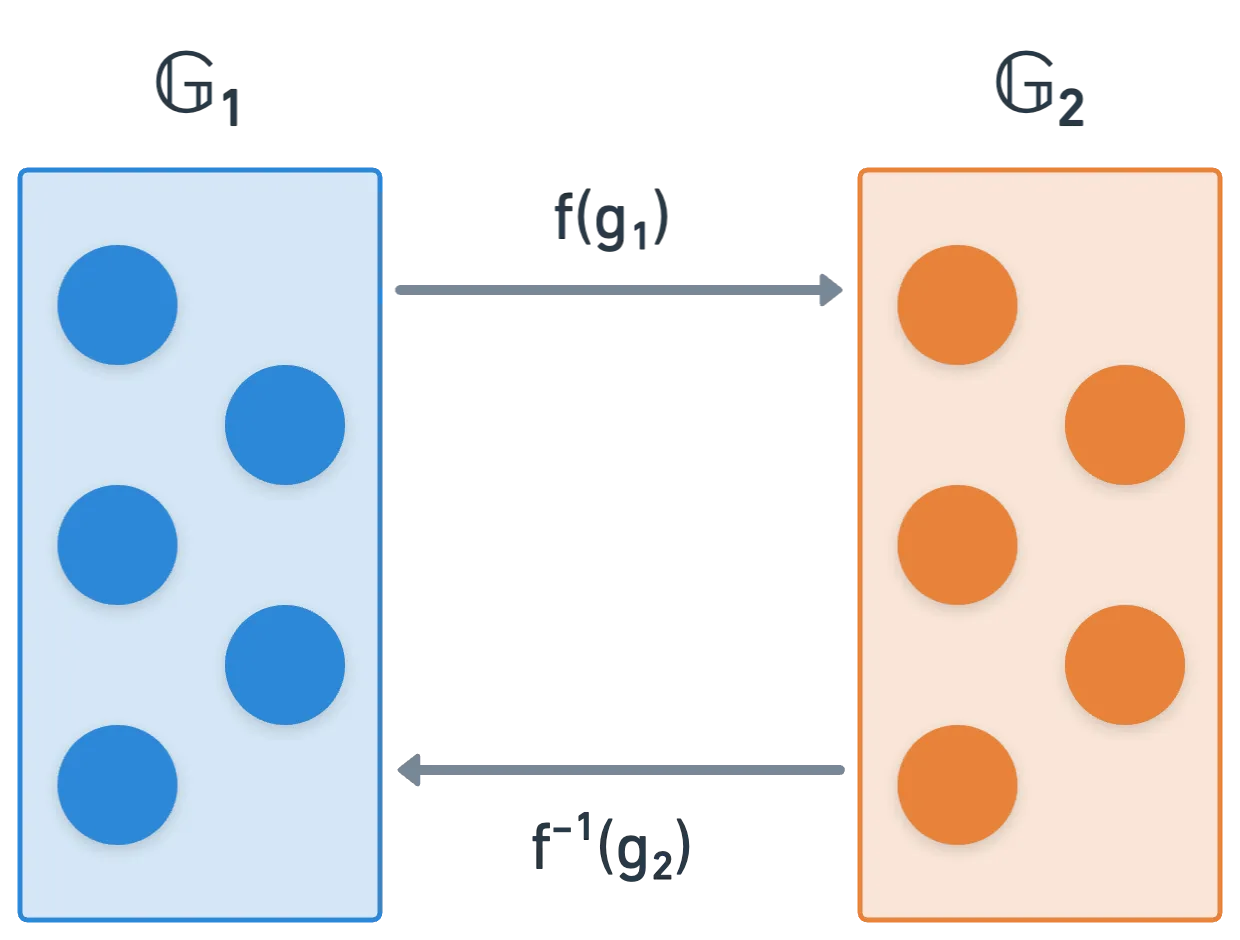
Um emparelhamento, também referido como um mapa bilinear, é realmente apenas uma função, tipicamente representada com a letra $e$. Ela recebe dois argumentos e produz uma única saída, assim:

$$e: \mathbb{G}_1 \times \mathbb{G}_2 \rightarrow \mathbb{G}_3 \ / \ e(G_1, G_2) = G_3$$

Vamos precisar de alguma notação da teoria dos conjuntos desta vez, mas nada muito louco.

Provavelmente a mais exótica (se você não teve muito contato prévio com teoria dos conjuntos) é o produto cartesiano — usado no conjunto $\mathbb{G}_1 \times \mathbb{G}_2$. É apenas o conjunto de todos os elementos da forma $(G_1, G_2)$ onde $G_1$ pertence a $\mathbb{G}_1$, e $G_2$ pertence a $\mathbb{G}_2$.

No entanto, esta não é uma função qualquer. Ela tem uma propriedade importante: é linear em ambas as entradas. Isso significa que todas as seguintes são equivalentes:

$$e([a]G_1, [b]G_2) = e(G_1, [b]G_2)^a = e(G_1, G_2)^ab = e([b]G_1, [a]G_2)$$

Como você pode ver, podemos fazer esse tipo de troca dos produtos (ou mais precisamente, operações de grupo). Mesmo que essa propriedade não pareça muito à primeira vista, ela é realmente muito poderosa.

Os emparelhamentos são uma espécie de liquidificador, no sentido de que não nos importamos muito com o valor particular obtido ao avaliar uma expressão de emparelhamento (exceto ao verificar algo chamado não-degeneração). Em vez disso, o que nos importa é que algumas combinações de entradas produzem o mesmo resultado, por causa da bilinearidade que mencionamos acima. Isso é o que os torna atraentes, como veremos mais adiante.

Curvas Elípticas e Emparelhamentos

Repare como as entradas vêm do produto cartesiano $\mathbb{G}_1 \times \mathbb{G}_2$. É um conjunto bem particular: $\mathbb{G}_1$ e $\mathbb{G}_2$ são grupos, para ser preciso. Grupos disjuntos, na verdade — significando que eles não compartilham nenhum elemento. Formalmente, dizemos que sua interseção é vazia:

$$|\mathbb{G}_1 \cap \mathbb{G}_2 = \varnothing$$

Além disso, $\mathbb{G}_1$ e $\mathbb{G}_2$ não são quaisquer grupos — eles devem ser adequados para o cálculo de emparelhamentos. Acontece que grupos de curvas elípticas são uma boa escolha — e uma muito boa em termos de eficiência computacional. Então é uma coincidência feliz que já tenhamos uma boa compreensão deles!

Se você verificar a literatura, há casos onde em vez de usar dois grupos disjuntos, você verá o mesmo grupo sendo usado duas vezes. Algo como $\mathbb{G} \times \mathbb{G}$.

Esses são às vezes chamados auto-emparelhamentos, e o que realmente acontece é que existe uma função f que mapeia $\mathbb{G}_2$ em $\mathbb{G}$ — significando que podemos transformar elementos de $\mathbb{G}_2$ em elementos de $\mathbb{G}$, e apenas usar $\mathbb{G}$ no nosso emparelhamento.

Embora não vamos cobrir como isso é feito, tenha em mente que a definição formal de um emparelhamento requer que os grupos sejam disjuntos.

Click to zoom

Aplicação

Antes de chegarmos ao ponto de "por que diabos estou aprendendo isso" (assumindo que ainda não estamos lá!), acredito ser frutífero apresentar uma aplicação.

Apesar do fato de que não sabemos como computar emparelhamentos ainda, podemos entender sua utilidade porque sabemos sobre suas propriedades.

Vamos não perder tempo e ir direto ao ponto.

A Configuração

Trabalhar com grupos de curvas elípticas, ou até com inteiros módulo $p$, pode te levar muito longe. Mas sabe uma coisa que nenhum deles pode fazer por você? Eles não permitem que você use sua identidade para operações criptográficas!

Identidade? Você quer dizer tipo meu nome? Parece loucura, mas pode ser feito. Alguma configuração é necessária, no entanto.

Para realizar esse tipo de façanha mágica criptográfica, vamos precisar de um ator especial, confiado por outras partes — frequentemente referido como Autoridade Confiável. Este ator será responsável pela geração de chaves privadas, então também é acuradamente (e muito descritivamente) chamado de Gerador de Chaves Privadas (PKG).

O PKG faz algumas coisas. Primeiro e mais importante, ele escolhe um segredo mestre, que é um inteiro $s$. Ele também escolhe e torna públicos alguns parâmetros públicos, que vamos definir em um minuto. E finalmente, ele escolhe e torna pública uma função de hash $H$, que faz hash para $\mathbb{G}_1$.

$$H: \{0,1\}^* \rightarrow \mathbb{G}_1$$

Para obter uma chave privada, André tem que solicitá-la do PKG. E para fazer isso, ele envia a eles sua identidade hasheada. Sua identidade pode ser qualquer coisa — um nome, um endereço de email, um número de documento de identidade, qualquer coisa que identifique unicamente um indivíduo. Vamos denotar isso como $ID$. Sua chave pública é então:

$$Q_A = H(ID_A) \in \mathbb{G}_1$$

Ao receber esse valor, o PKG calcula sua chave privada como:

$$S_A = [s]Q_A \in \mathbb{G}_1$$

E a envia para André.

Todas essas comunicações são assumidas como acontecendo por um canal seguro. Em particular, a chave secreta de André não deve vazar!

Click to zoom

Nossa configuração está pronta! André tem tanto sua chave privada quanto pública. O que ele pode fazer com isso?

Encriptação Baseada em Identidade

Vamos supor que André quer encriptar uma mensagem para Bruna. Tudo que ele tem é a chave pública dela, porque ele conhece a identidade dela ($ID$). E apenas fazendo o hash, ele obtém a chave pública dela:

$$Q_B = H(ID_B)$$

Também vamos precisar de mais algumas coisas:

• Um ponto $P \in \mathbb{G}_2$, usado para calcular um ponto $Q = [s]P$, também em $\mathbb{G}_2$. Como $s$ é apenas conhecido pela autoridade confiável, esses pontos são calculados e publicados pelo PKG — eles são os parâmetros públicos que mencionamos anteriormente, e vamos denotá-los por $p$:

$$p = (P, Q)$$

• Também precisamos de outra função de hash $H'$:

$$H': \mathbb{G}_3 \rightarrow \{0,1\}^n$$

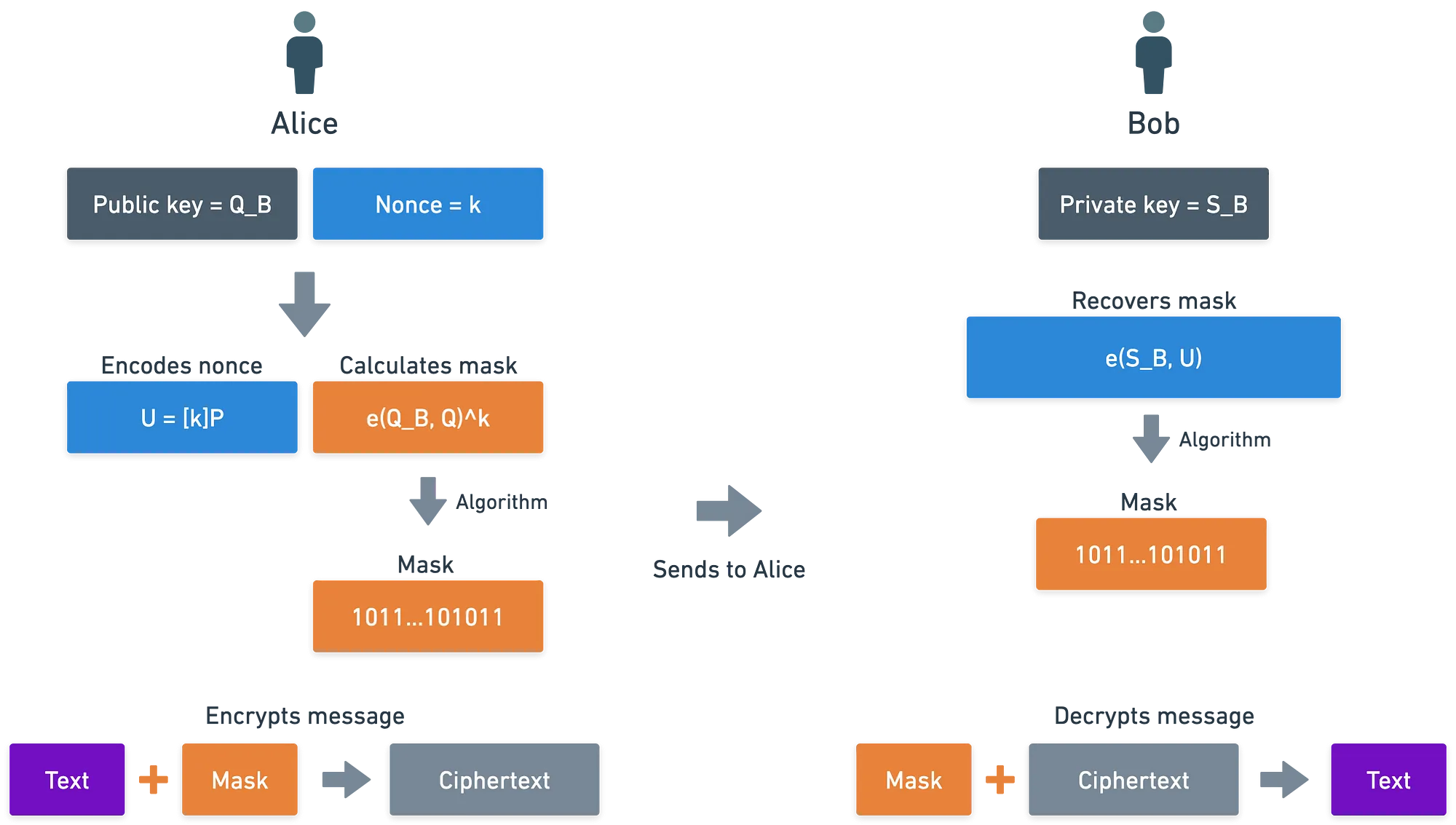
Este esquema de encriptação usa uma estratégia similar ao Esquema de Encriptação Integrado de Curva Elíptica que vimos anteriormente na série: mascaramento. Então, para encriptar uma mensagem $M$, André segue estes passos:

• Ele escolhe um nonce aleatório, que é um inteiro $k$.
• Com ele, ele calcula $U = [k]P$. Isso será usado para mais tarde reconstruir a máscara.
• Então, usando a chave pública de Bruna, que é apenas o hash da identidade dela, ele computa:

$$e(Q_B,Q)^k$$

• Ele usa esse valor para computar uma máscara, que é adicionada à mensagem:

$$V = M \oplus H'(e(Q_B,Q)^k)$$

A mensagem final encriptada será a tupla $(U, V)$.

Lembre-se que o símbolo $\oplus$ representa a operação XOR. E uma das propriedades dessa operação é: $M \oplus A \oplus A = M$. O que isso significa é que adicionar a máscara duas vezes nos permite recuperar a mensagem original.

Como Bruna decripta? Bem, ela pode pegar $U$ e simplesmente recalcular a máscara. Com ela, ela re-obtém a mensagem original:

$$M = V \oplus H'(e(S_B,U))$$

Mas espere... Como as duas máscaras são iguais? Claramente, elas não parecem ser a mesma coisa... São avaliações diferentes do emparelhamento!

$$e(Q_B,Q)^k \stackrel{?}{=} e(S_B,U)$$

Não tema — prometo que isso faz sentido. Porque isso é precisamente onde a mágica dos emparelhamentos acontece: usando sua propriedade de bilinearidade, podemos mostrar que os dois valores são equivalentes:

$$e(Q_B,Q)^k = e(Q_B, [s]P)^k = e(Q_B, P)^{s.k} = e([s]Q_B, [k]P)$$ $$e(Q_B,Q)^k = e(S_B, U)$$

E assim, conhecer apenas a identidade de Bruna é suficiente para André encriptar informação só para ela — impulsionado por emparelhamentos, claro!

Click to zoom

De Volta aos Emparelhamentos

Okay, agora que vimos emparelhamentos em ação, estamos totalmente motivados a entender como eles são definidos um pouco mais em profundidade. Certo? Certo?

Isso não vai demorar muito — vamos apenas dar uma olhada rápida em algumas das ideias que tornam os emparelhamentos possíveis.

Mencionamos que $\mathbb{G}_1$ e $\mathbb{G}_2$ poderiam muito bem ser grupos de curvas elípticas.

Então, apenas escolhemos duas curvas elípticas diferentes? Bem, nesse caso, teríamos que ter certeza de que os grupos são disjuntos, o que não é necessariamente fácil; e há outras preocupações em tal cenário.

E quanto a usar uma única curva elíptica? Então precisaríamos de dois subgrupos diferentes. Quando fazemos uso de um gerador de grupo, $G$, o grupo gerado por ele não é necessariamente a totalidade do grupo de curva elíptica — mas poderia ser. Essa relação de inclusão é escrita como:

$$|\langle G \rangle \subseteq E(\mathbb{F}_q)$$

O que significa: o grupo gerado por $G$ é ou um subgrupo, ou toda a curva elíptica.

Geralmente queremos que a ordem do subgrupo gerado por $G$ seja a maior possível, para que o problema DLP seja difícil. Isso significa que:

• Se há outros subgrupos, eles são provavelmente pequenos.
• Se $\langle G \rangle$ é a totalidade da curva elíptica, então não há outros subgrupos disponíveis.

Parece que chegamos a um dilema...

Expandindo a Curva

Felizmente, esta pequena crise nossa tem uma solução. Veja, nossas curvas sempre foram definidas sobre os inteiros módulo $q$ — mas e se pudéssemos estender os valores possíveis que usamos?

Em vez de apenas permitir que os pontos na curva elíptica assumam valores nos inteiros módulo $q$:

$$|\mathbb{F}_q = \{0,1,2,3,..., q-1\}$$

Poderíamos usar algo como os números complexos, e permitir que os pontos em $E$ assumam valores neste conjunto:

$$|\mathbb{F}_{q^2} = \{a + bi : a, b \in \mathbb{F}_q, i^2 + 1 = 0 \}$$

Usar números complexos faz perfeito sentido: por exemplo, você pode verificar por si mesmo que o ponto $(8, i)$ está na seguinte curva elíptica:

$$E/\mathbb{F}_{11}: y^2 = x^3 + 4$$

Extensões de Corpo

Números complexos são apenas um exemplo de um conceito mais geral, que é extensões de corpo.

Um corpo (vamos denotá-lo $F$) é apenas um conjunto com algumas operações associadas. Isso provavelmente soa familiar — é uma definição muito similar à que demos para grupos, bem no início da série.

Independente da formalidade, há um corpo muito importante com o qual devemos nos importar: os inteiros módulo $q$, quando $q$ é um número primo.

Isso pode soar um pouco enganador. Originalmente, eu te disse que os inteiros módulo $q$ eram um grupo. E de fato, se usarmos uma única operação (como adição), eles se comportam como um grupo.

Mais geralmente, no entanto, eles são um corpo, pois suportam adição, subtração, multiplicação e divisão (bem, inversões modulares, na verdade!).

Uma extensão de corpo é simplesmente um conjunto $K$ que contém o corpo original:

$$F \subset K$$

Sob a condição de que o resultado de operações entre elementos de $F$ sempre estão em $F$, mas nunca no resto de $K$ (o conjunto $K {-} F$).

Uma extensão de corpo muito conhecida é, claro, o conjunto dos números complexos. Os números reais atuam como $F$, e operações entre números reais (adição, subtração, multiplicação e divisão) estão nos números reais ($F$) também. Operações entre números complexos podem ou não resultar em números reais.

Por que isso importa? Imagine que definimos uma curva sobre os inteiros módulo $q$. Obtemos um monte de pontos, que podemos denotar:

$$E(F)$$

Se estendermos o corpo base (os inteiros módulo $q$), então novos pontos válidos aparecerão, enquanto preservamos os antigos. Isto é:

$$E(F) \subseteq E(K)$$

Por causa disso, novos subgrupos aparecem, e obtemos o bônus adicional de manter os subgrupos originais, que foram definidos sobre o corpo base.

E quando escolhemos uma extensão de corpo apropriada, algo incrível acontece: obtemos uma infinidade de subgrupos com a mesma ordem que $\langle G \rangle$. E esses grupos acontecem de ser quase disjuntos: eles apenas compartilham o elemento identidade, $\mathcal{O}$. O conjunto de todos esses subgrupos é o que é chamado de grupo de torção.

Click to zoom

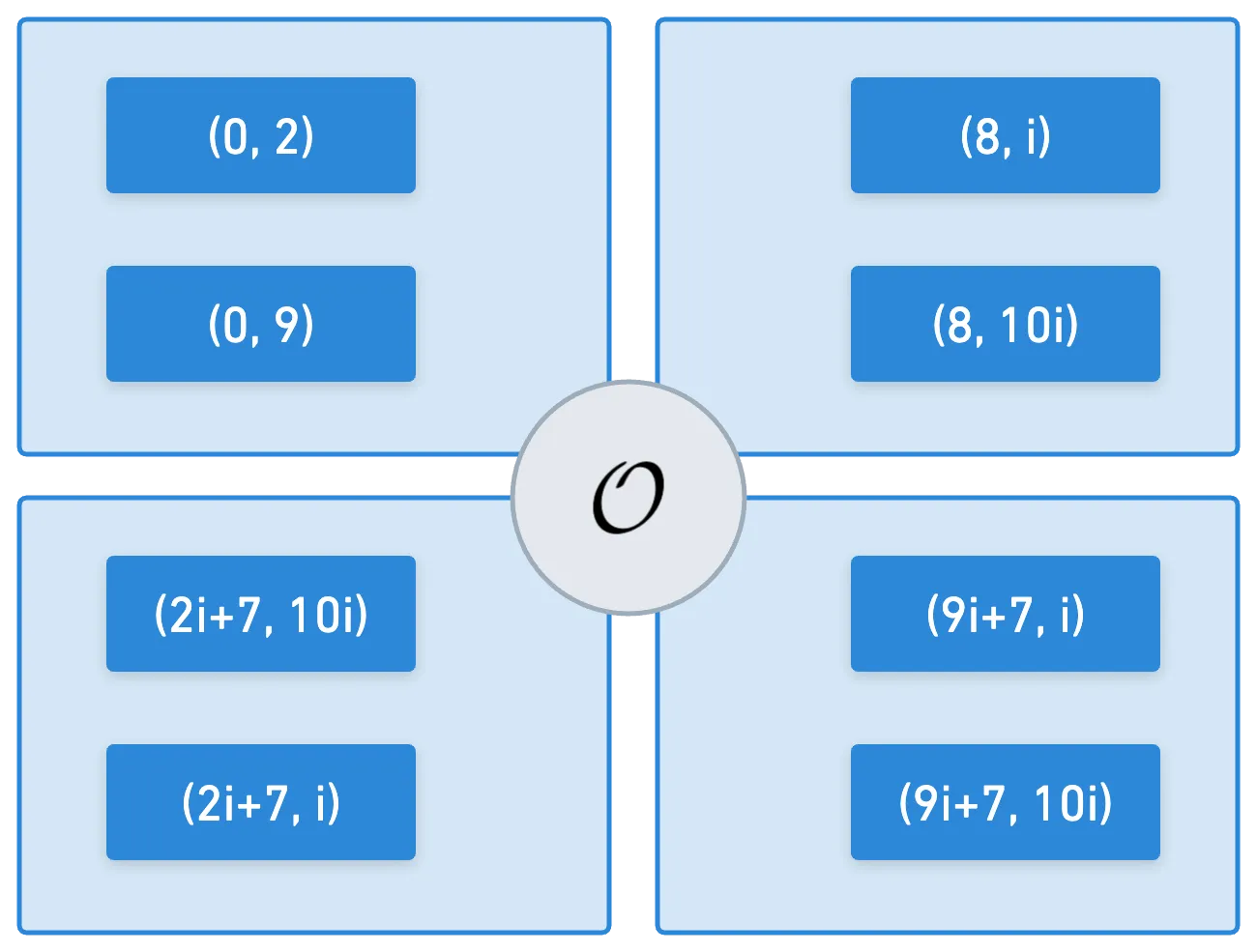
Okay, vamos parar por aí. O objetivo desta seção é apenas apresentar uma ideia geral do que são as entradas de emparelhamento. No entanto, não há muito mais que possamos dizer sem fazer um mergulho mais profundo no assunto, o que é algo que excede o escopo deste artigo introdutório.

Novamente, recomendo este livro se você quiser uma explicação mais detalhada — e por sua vez, ele referencia alguns ótimos recursos mais avançados.

A ideia importante aqui é que o cálculo de emparelhamento não é trivial, de forma alguma. Se você está interessado em eu expandir este tópico mais em artigos seguintes, por favor me avise!

Resumo

Embora não tenhamos nos aventurado profundamente no território dos emparelhamentos, esta simples introdução nos permite entender o princípio de funcionamento por trás de métodos baseados em emparelhamento. Tudo depende da propriedade de bilinearidade que vimos logo no início do artigo.

A conclusão chave aqui é:

Emparelhamentos são esses tipos de liquidificadores, onde nos importamos com o resultado computado ser o mesmo para dois conjuntos diferentes de entradas

Novamente, podemos mergulhar no cálculo de emparelhamentos mais tarde. Acredito ser mais frutífero começar a ver algumas aplicações.

Por essa razão, vamos olhar para mais algumas aplicações de emparelhamentos na próxima parte da série. Te vejo lá!