Curvas Elípticas En Profundidad (Parte 7)

No debe haber sido un viaje fácil para llegar hasta aquí.

Hemos cubierto una amplia gama de conceptos, desde cosas simples hasta algunas ideas muy abstractas.

Bueno, si has sentido que las cosas han sido complicadas hasta ahora... Agárrate a lo que tengas a mano. Las cosas están a punto de volverse completamente locas.

Porque hoy, hablaremos de emparejamientos. Y en un fuerte contraste con mi artículo anterior sobre el tema, esta vez llegaremos a los detalles más finos y complejos.

Como consecuencia, los emparejamientos serán abordados en tres entregas consecutivas: la primera (esta) se centrará en establecer algunos fundamentos sobre los que luego definiremos los emparejamientos en la segunda parte (próximo artículo), y luego discutiremos algunos otros detalles para cerrar este asunto en la tercera parte.

Va a ser un artículo largo. Respira profundo. Toma una taza de café. ¿Listo? Comencemos.

Emparejamientos en Pocas Palabras

En primer lugar, ¿qué es un emparejamiento?

Hablando informalmente, un emparejamiento o mapa bilineal es una función que toma dos entradas, cada una perteneciente a un grupo, y devuelve un elemento de otro grupo. Más formalmente, escribimos:

$$e: \mathbb{G}_1 \times \mathbb{G}_2 \to \mathbb{G}_3$$

Ahora, esta no es cualquier tipo de función - para que sea un emparejamiento, debe tener una propiedad muy peculiar. Esta propiedad se llama bilinealidad: significa que es lineal en ambas entradas.

¿Qué quiero decir con esto? Supongamos que las operaciones de grupo pueden representarse con $+$, $\cdot$, y $*$ para $\mathbb{G}_1$, $\mathbb{G}_2$, y $\mathbb{G}_3$ respectivamente. La bilinealidad esencialmente significa que ambas igualdades se cumplen:

$$e(x + y, z) = e(x,z) * e(y, z)$$ $$e(x, y \cdot z) = e(x,y) * e(x, z)$$

No parece tan loco, lo sé. Pero esta característica permite mover cosas de manera inteligente. Por ejemplo, es fácil ver que:

$$e(x^n, y) = e(x,y^n)$$

Me tomé la libertad de usar notación exponencial, porque siempre podemos encontrar un isomorfismo a la forma multiplicativa de todos modos. Pero ten en cuenta que el exponente significa la aplicación repetida de la operación del grupo.

Este tipo de pequeños trucos que podemos hacer con los emparejamientos permiten todo tipo de primitivas criptográficas interesantes, como el cifrado basado en identidad (IBE), y herramientas que son esenciales para algunas pruebas de conocimiento cero modernas. Entre otras, por supuesto.

Y eso es el final de la parte fácil.

El problema ahora es que necesitamos encontrar grupos adecuados, y también definir alguna función que se comporte como un mapa bilineal. Por supuesto, podemos inferir que esos grupos tienen que ver con nuestras confiables curvas elípticas. Pero no es tan simple como elegir dos curvas aleatorias - necesitaremos mucho más que eso para que esto funcione.

En particular, necesitamos revisar la estructura de grupo de las curvas elípticas una vez más.

Subgrupos de Curvas Elípticas

En el artículo anterior, exploramos cómo la estructura de un grupo de curva elíptica podía describirse mediante el teorema de Mordell-Weil:

$$E(\mathbb{Q}) \simeq E(\mathbb{Q})_{\textrm{tors}} \oplus \mathbb{Z}^r$$

Donde podíamos separar entre los subgrupos de orden infinito (que son isomórficos a los enteros), y subgrupos de orden finito.

Los grupos de curvas elípticas sobre campos finitos son, como sabemos, finitos - solo hay una cantidad limitada de puntos que puedes colocar en una cuadrícula $p \times p$. Por lo tanto, esos subgrupos de orden infinito no son realmente tan importantes para nosotros - y tiene más sentido centrarse en los de orden finito.

Al escalar la curva por un factor apropiado, podemos asegurar que cada punto en esos subgrupos finitos no solo sea racional, sino de valor entero. Así es como obtenemos nuestros grupos de curvas elípticas sobre campos finitos.

Estos subgrupos en los que nos estamos centrando son bastante especiales, y tienen su propio nombre: se llaman grupos de torsión.

Y son exactamente lo que necesitamos para construir emparejamientos.

Grupos de Torsión

Los grupos de torsión son los subgrupos donde, para algún entero $r$, todos sus elementos $P$ tienen la propiedad de resultar en $\mathcal{O}$ cuando se multiplican por $r$. Básicamente, $[r]P = \mathcal{O}$ para cada punto del subgrupo. Escribimos esto como $E[r]$ - la r-torsión de $E$.

Además, si $P$ es un generador de $E[r]$, podemos ver que cada otro punto en el subgrupo también pertenece a la torsión porque $[r]([n]P) = [n]([r]P) = [n]\mathcal{O} = \mathcal{O}$.

Por esta razón, el grupo $E[r]$ es también el núcleo del mapa $[r]: P \rightarrow P$, o multiplicación por $r$. Recuerda que el núcleo es solo la idea generalizada de raíces.

Ahora volvemos a los campos finitos. Como se mencionó anteriormente, está claro que todo el grupo de curva elíptica es finito. Sin embargo, vale la pena recordar que es altamente no trivial encontrar puntos de valor entero en una curva elíptica, como exploramos en el artículo anterior.

También está claro que, dado que tenemos una cantidad limitada de puntos con los que trabajar, tenemos garantizados algunos subgrupos cíclicos. Como máximo, todo el grupo será un solo ciclo de algún tamaño $r$.

Lo que sigue es bastante desconcertante. Hay un teorema, llamado el teorema de estructura para grupos abelianos finitos (ese es un nombre bastante largo), que establece que:

$$E[r] \approx \mathbb{Z}_r \times \mathbb{Z}_r$$

Lo que significa que hay algún isomorfismo entre estos dos grupos, lo que también significa que tienen el mismo tamaño (es una correspondencia uno a uno).

Piensa en las consecuencias de esto. Está diciendo que la r-torsión debería tener un tamaño de $r^2$. Si $r$ es mayor que $p$ (el tamaño de nuestro campo finito), ¡ni siquiera tenemos tantos puntos disponibles!

Por lo tanto, la búsqueda de estos puntos restantes nos obliga a mirar las extensiones de campo.

Extendiendo la Curva

Trabajar con extensiones de campo no es un concepto nuevo para nosotros. Ya sabemos cómo funcionan: adjuntamos algunos elementos a nuestro campo finito, haciendo que crezca mucho más. Un ejemplo de esto fue la extensión compleja: al agregar $i$ al campo - de modo que $i^2 + 1 = 0$ -, de repente aparecen una gran cantidad de nuevos números (complejos) en el campo extendido, y su tamaño crece a $p^2$.

Del mismo modo, hay más puntos disponibles. Algunos de estos también cumplen con la ecuación de la curva elíptica $E$, por lo que el grupo de la curva elíptica también crece en tamaño.

Los números complejos son una especie de elección obvia aquí - pero no son la única opción disponible. De hecho, podemos lograr extensiones con cualquier tamaño $p^k$, donde $k$ es un entero llamado el grado de la extensión.

Quiero ser preciso aquí. Trabajemos con $\mathbb{F}_{17}$ una vez más. Supongamos que quisiéramos extender el campo agregando un elemento $\alpha$, tal que $\alpha^3 - 2 = 0$. El problema es que esta ecuación tiene una solución en ese campo: ¡$8$! Puedes comprobarlo tú mismo.

Así que debemos tener cuidado de que el elemento que elijamos tenga sentido. Si intentamos la misma extensión en $\mathbb{F}_7$ en su lugar, verás que $\alpha^3 - 2 = 0$ no tiene solución en el campo, por lo que esta es una extensión válida de grado tres, con un total de $7^3$ elementos.

Podemos crear extensiones de cualquier grado - y el grado en sí viene dado por la potencia más alta en la condición polinómica que imponemos al nuevo elemento que adjuntamos al campo.

Extensiones y Torsión

Con esto en mente, podemos volver a esta expresión aquí:

$$E[r] \approx \mathbb{Z}_r \times \mathbb{Z}_r$$

Y nos preguntamos: ¿cuál es el $k$ más pequeño que necesitamos para encontrar todos nuestros puntos de r-torsión faltantes?

Este $k$ más pequeño tiene un nombre especial en este contexto: se llama el grado de inmersión. Es el entero positivo más pequeño tal que $r$ divide $p^k - 1$, que es el tamaño del grupo en el campo extendido.

Esto también se escribe como $r | (p^k - 1)$, que significa "$r$ divide $(p^k - 1)$".

A primera vista, este requisito puede no parecer suficiente - después de todo, no garantiza que todos los $r^2$ puntos de la r-torsión pertenezcan a nuestro campo. Sin embargo, resulta que esta condición es generalmente suficiente. Tiene que ver con que el campo contenga las raíces r-ésimas de la unidad, que son algunos elementos de campo $z$ tales que $z^r \ \textrm{mod}\ p = 1$.

Todo lo que realmente necesitamos es que $r$ sea primo.

Muy bien, digamos que hemos encontrado una extensión de campo adecuada. ¿Y ahora qué?

Veamos. Sabemos que la r-torsión tiene $r^2$ elementos. También sabemos que cada subgrupo en la r-torsión tiene $r$ elementos. Y todos esos grupos tienen un elemento en común: $\mathcal{O}$. Así que cada uno de ellos tiene $r - 1$ elementos diferentes.

Esto significa que en total, hay $r + 1$ subgrupos en la r-torsión. Esto es porque:

$$(r + 1)(r - 1) = r^2 - 1$$

Y si también contamos $\mathcal{O}$, ¡llegamos al gran total de $r^2$ puntos!

Lo que originalmente era un solo subgrupo en el campo base, sufre una especie de evolución, y se transforma en muchos más grupos.

Click to zoom

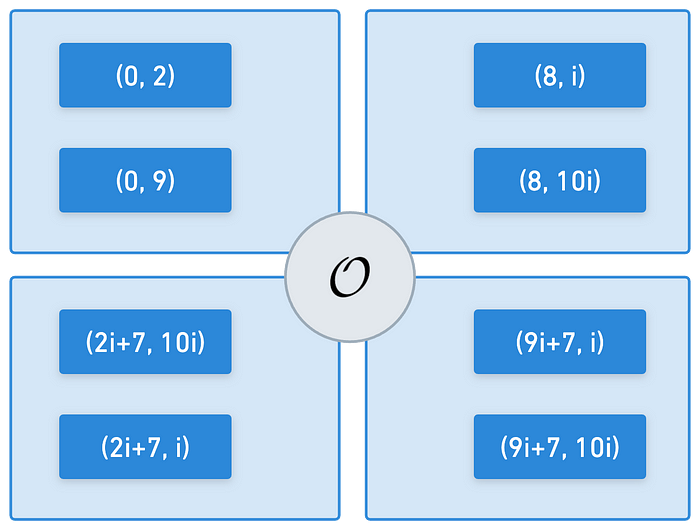
Estos subgrupos serán la clave para construir emparejamientos.

Todavía tenemos un par de cosas que decir sobre estos grupos antes de ver realmente cómo construir emparejamientos. Mantente fuerte, amigos.

El Mapa de Traza

Parte de lo que hace útiles a estos subgrupos de torsión es la existencia de algunos mapas o funciones entre ellos con propiedades muy especiales.

Ya hemos hablado de los twists en curvas, como un ejemplo notable.

Otra función de este tipo es lo que se llama el mapa de traza, denotado por $\textrm{Tr}$. Su definición es bastante compleja. Así es como se ve:

$$\textrm{Tr}(P) = \sum_{\sigma \in Gal(\mathbb{F}_{p^k} / \mathbb{F}_{p})} \sigma (P) = \sum_{i=0}^{k-1} \pi ^i(P) = \sum_{i=0}^{k-1} (x^{p^i}, y^{p^i})$$

Lo sé. ¿Qué demonios es eso?.

Vamos a descomponer esto pieza por pieza.

La función $\pi$ es solo el endomorfismo de Frobenius del que hablamos hace un par de artículos. Vimos cómo actuaba trivialmente sobre elementos del campo base - pero para la extensión de campo, es otra historia. Generalmente, aplicar el endomorfismo producirá algún otro punto.

Pero, ¿qué demonios es ese $\sigma$? De nuevo, es algo que ya hemos visto: un elemento del grupo de Galois del campo.

Como recordatorio rápido, un grupo de Galois es básicamente una colección de automorfismos de campo. Los automorfismos simplemente reorganizan elementos, pero preservan la estructura del campo. En el caso de nuestra extensión, se espera que estos automorfismos dejen sin cambios los elementos en el campo base $\mathbb{F}_p$.

Para campos finitos, el grupo de Galois es cíclico (un ciclo de funciones), generado por el endomorfismo de Frobenius - cada elemento $\sigma$ es solo alguna potencia de $\pi$, que es lo que vemos en la fórmula.

El mapa de traza tiene una propiedad interesante: mapea elementos en la extensión de campo al campo base - es una especie de proyección o aplastamiento.

Es fácil probar esto mostrando que $\pi(\textrm{Tr}(P)) = \textrm{Tr}(P)$. ¡Te lo dejo como ejercicio!

Y tiene otra propiedad aún más loca: es lineal. Es decir, para cualquier punto $P$ y $Q$, entonces $\textrm{Tr}(P + Q) = \textrm{Tr}(P) + \textrm{Tr}(Q)$. Esto no es evidente a primera vista, pero podemos ver por qué es así examinando cada uno de los componentes del mapa de traza - que son potencias del endomorfismo de Frobenius.

Esencialmente, para que esto funcione, esta igualdad debería cumplirse:

$$(a + b)^p \ \textrm{mod}\ p = (a^p + b^p) \ \textrm{mod}\ p$$

Y mágicamente, en campos finitos, esto funciona. La fórmula expandida sería:

$$(a + b)^p \ \textrm{mod}\ p = \sum_{k=0}^{p}\begin{pmatrix} p \\ k \end{pmatrix}a^{(p-k)}b^k$$

Todos los coeficientes resultan ser divisibles por $p$, excepto los de $a^p$ y $b^p$ - lo que significa que dichos coeficientes son congruentes a $0$ módulo $p$, ¡así que desaparecen!

Esto se conoce como "el sueño del estudiante de primer año". ¡Lo que no te dicen es que funciona para campos finitos!

Por lo tanto, el endomorfismo de Frobenius es lineal, también lo son sus potencias, y también lo es la traza.

La linealidad del mapa de traza también garantiza una cosa adicional. Cuando se aplica a la r-torsión, ya sabemos que obtendremos un grupo en el campo base. Pero el resultado también pertenecerá a un subgrupo en la r-torsión. Porque la linealidad hace que:

$$\textrm{Tr}([r]P) = [r]\textrm{Tr}(P)$$

Si $P$ es un punto en la r-torsión, entonces $[r]P = \mathcal{O}$. Así que $[r]\textrm{Tr}(P)$ será igual a $\textrm{Tr}(\mathcal{O})$, que por definición es $\mathcal{O}$.

Estructura de Torsión

Para cerrar las cosas, quiero hablar un poco sobre algunos subgrupos especiales en la r-torsión. Nuevamente, todos estos serán importantes para la construcción de emparejamientos.

Sobre el campo base, (a menudo) obtenemos un solo subgrupo en la r-torsión. Esto a menudo se llama el subgrupo del campo base, y lo denotamos por $\mathcal{G}_1$. Cuando aplicamos el mapa de traza a un subgrupo de torsión, este es exactamente el grupo que obtenemos, así que podríamos decir:

$$\textrm{Tr}: E[r] \to \mathcal{G}_1$$

Ahora, te presentaré una forma extrañamente complicada de escribir $\mathcal{G}_1$. Se puede escribir como:

$$\mathcal{G}_1 = E[r] \cap \textrm{Ker}(\pi - [1])$$

$\textrm{Ker}$ solo significa núcleo. Hemos hablado de esto lo suficiente en el pasado, pero es simplemente el conjunto de puntos que, cuando aplicamos el endomorfismo en cuestión (la función $\pi - [1]$), obtenemos $\mathcal{O}$. Y sabemos que $\pi$ actúa trivialmente en el campo base - por lo que ese núcleo es exactamente $\mathbb{F}_p$.

$\mathcal{G}_1$ es entonces el conjunto de puntos en la r-torsión que pertenecen al campo base.

Decimos que $\mathcal{G}_1$ es el espacio propio [1] de $\pi$ restringido a $E[r]$. Espacio propio por supuesto se refiere a la idea de valores propios, que en el contexto de curvas elípticas, son valores $\lambda$ asociados con conjuntos de puntos $P$ tales que:

$$\pi(P) = [\lambda]P$$

Entonces, $1$ es un valor propio del endomorfismo de Frobenius. Pero no es su único valor propio.

El Polinomio Característico

El segundo valor propio no es tan evidente, y para encontrarlo, necesitamos conocer el polinomio característico del endomorfismo de Frobenius.

Para hacerlo breve, el polinomio característico es esta función aquí:

$$\pi^2(P)- [t](\pi(P)) + [p]P = \mathcal{O}$$

Explicar de dónde viene esto probablemente tomaría otro artículo completo - así que de nuevo, te pido un pequeño acto de fe.

La $t$ en esa ecuación es un valor interesante: es la traza de Frobenius. Esencialmente, si el tamaño de nuestro grupo de curva elíptica es $\#E$, entonces $t = \#E - p + 1$.

Para encontrar los valores propios de $\pi$, asumimos que $\pi(P) = [\lambda]P$, y sustituimos en la ecuación anterior, obteniendo:

$$[\lambda^2 - t\lambda + p]P = \mathcal{O}$$

Para que esto sea cierto, requerimos que el valor entre corchetes sea $0$. Y esto produce dos resultados - llamémoslos $\alpha$ y $\beta$. Son los valores propios, y usando algo de álgebra básica, sabemos que deberían cumplir dos condiciones:

• $\alpha + \beta = t$
• $\alpha \beta = p$

La segunda es particularmente importante - ya sabemos que uno de los valores propios es $1$. Por lo tanto, ¡el otro debe ser $p$!

Usando este segundo valor propio (y su espacio propio asociado), ahora podemos reciclar esa extraña definición de antes, pero usando este resultado recién encontrado:

$$\mathcal{G}_2 = E[r] \cap \textrm{Ker}(\pi - [p])$$

En otras palabras, $\mathcal{G}_2$ consiste en puntos $P$ en la r-torsión tales que $\pi(P) = [p]P$.

Estos grupos ($\mathcal{G}_1$ y $\mathcal{G}_2$) son muy especiales. Tomemos un momento para hablar de ellos.

Como ya mencionamos, $\mathcal{G}_1$ se llama el subgrupo del campo base, lo cual tiene sentido, ya que sabemos que vive completamente en el campo base. En contraste, $\mathcal{G}_2$ existe completamente en la extensión de campo.

Esto tiene sentido porque cualquier punto $P$ en $\mathcal{G}_2$ debería satisfacer $\pi(P) = [p]P$, y si $P$ perteneciera al campo base, entonces tendríamos $P = [p]P$. Y esto no es cierto para puntos en la r-torsión, a menos que $r$ divida $p$. Como tanto $r$ como $p$ son usualmente primos, concluimos que $\mathcal{G}_2$ no debe existir en el campo base.

Ambos son subgrupos cíclicos de orden $r$, porque pertenecen a la r-torsión. Su intersección es exactamente el punto $\mathcal{O}$. Y en conjunto, tienen una propiedad notable: generan toda la r-torsión.

Hay muchas pistas de esto. Por ejemplo, el hecho de que $E[r]$ sea isomórfico a $\mathbb{Z}_r \times \mathbb{Z}_r$ - un espacio de "dimensión 2" sobre $\mathbb{Z}_r$. Además, el polinomio característico también tenía grado dos. Estas pistas sugieren que solo dos espacios propios de la r-torsión son suficientes para generarla completamente - lo que simplemente significa que cualquier punto $P$ en $E[r]$ puede descomponerse de forma única como $P = P_1 + P_2$, donde $P_1 \in \mathcal{G}_1$, y $P_2 \in \mathcal{G}_2$.

Oh, y tenemos que bautizar a $\mathcal{G}_2$ con un nombre. Lo llamamos el subgrupo de traza cero, ya que todos los puntos $P$ en $\mathcal{G}_2$ tienen $\textrm{Tr}(P) = \mathcal{O}$. ¡No mostraremos por qué es así aquí, pero de nuevo, siéntete libre de intentarlo tú mismo!

Redondeando las cosas, sabemos que el mapa de traza toma puntos en $E[r]$ hacia $\mathcal{G}_1$. ¿Y qué hay de $\mathcal{G}_2$? ¿Hay algún mapa que haga lo mismo? De hecho, lo hay, y se llama el mapa de anti-traza, definido como:

$$a\textrm{Tr} : P \to P' \ / \ a\textrm{Tr}(P)= [k]P - \textrm{Tr}(P)$$

Por supuesto, necesitaríamos mostrar que $\textrm{Tr}(a\textrm{Tr}) = \mathcal{O}$. Ese esfuerzo, amigo mío, te lo dejo a ti.

Resumen

Si has llegado a este punto, no hay manera de que no sientas que has sido golpeado por un camión lleno de rareza matemática.

Sé que esto ha sido intenso. Sé que a veces, no es divertido. He hecho mi mejor esfuerzo para tratar de mantenerlo claro y algo entretenido - pero las matemáticas a este nivel son desafiantes sin importar cómo lo mires, y dondequiera que mires, hay más y más teoría en la que profundizar.

Aun así, seguramente hemos cubierto mucho terreno hoy.

Recapitulemos: introdujimos la idea de emparejamientos o mapas bilineales. Mencionamos cómo construir tales funciones no es fácil, y cómo necesitaremos algunos grupos especiales como entradas.

Luego procedimos a presentar esos grupos, explorando la r-torsión en extensiones de campo, e introduciendo el subgrupo del campo base ($\mathcal{G}_1$) y el subgrupo de traza cero ($\mathcal{G}_2$) como generadores para la r-torsión. Y vimos cómo el mapa de traza y el mapa de anti-traza nos permiten aplastar elementos en la r-torsión en $\mathcal{G}_1$ o $\mathcal{G}_2$.

Desde la perspectiva de una persona curiosa, diré que encuentro las cosas que hemos visto hoy increíblemente asombrosas y hermosas por derecho propio.

Por supuesto, nos hemos perdido la cereza del pastel: qué papel tienen estas cosas en la construcción de emparejamientos.

Y ese será el tema del próximo artículo. ¡Nos vemos entonces!