Curvas Elípticas En Profundidad (Parte 6)

La última vez, aprendimos a hablar el lenguaje de los divisores. Esto es extremadamente importante para obtener una comprensión más profunda de las curvas elípticas, y es crucial para entender los emparejamientos — una construcción que abordaremos en los próximos artículos.

Pero antes de eso, quiero tomarme el tiempo para sumergirnos realmente en la teoría y explorar algunas cosas que normalmente damos por sentadas durante nuestro análisis, pero que de hecho no son evidentes en absoluto.

Lo prometo — este será el último tramo de teoría extraña (¡antes de llegar a los emparejamientos, al menos!).

Dicho esto, este artículo es quizás menos práctico que los otros, y más centrado en la teoría pura. Aun así, hoy hablaremos de temas que se asocian estrechamente con la capacidad de contar puntos en curvas elípticas. Algo super importante, pero que no cubriremos hoy.

Sin más preámbulos, ¡ahí vamos!

Puntos Racionales

Una de las suposiciones fundamentales cuando trabajamos con curvas elípticas sobre campos finitos, es que existen puntos en la curva con coordenadas enteras.

Puntos como $(1,1)$, $(2,3)$, o $(5,8)$.

Piensa en esto por un segundo. ¿Te parece evidente? ¿Podemos siempre encontrar estos puntos de valor entero?

Más generalmente, podríamos intentar encontrar puntos racionales: puntos cuyas coordenadas son números racionales. Dependiendo de la curva, determinar si la curva tiene puntos racionales o no puede ser muy fácil, o extremadamente complejo.

De hecho, encontrar puntos racionales en curvas es un ejemplo clásico de ecuaciones diofánticas — ecuaciones polinómicas donde el objetivo es encontrar soluciones enteras o racionales.

El Último Teorema de Fermat, que tomó más de 350 años para probarse, es quizás el ejemplo más famoso.

Adivina en cuál de las dos categorías caen las curvas elípticas...

Sí, por supuesto que caen en la última.

Para obtener una buena comprensión de las ideas detrás de la búsqueda de puntos racionales, centrémonos primero en una curva familiar, donde resulta ser realmente fácil encontrarlos: un círculo.

Puntos Racionales en el Círculo

Los círculos están representados por esta simple ecuación:

$$x^2 + y^2 = R^2$$

Donde $R$ es el radio. ¿Cómo encontraríamos puntos racionales en esta curva?

Comencemos tratando de encontrar al menos uno. Resulta que todos los puntos donde el círculo interseca los ejes son racionales: $(1,0)$, $(0,1)$, $(-1,0)$, y $(0,-1)$.

¡Gran comienzo! Ahora, usaremos estos puntos como semillas. Toma el punto $(0,1)$, por ejemplo. Luego, dibuja una línea que pase por él, que tenga una pendiente racional $m$, que podemos escribir como $m_1 \ / \ m_2$. Si calculas la ecuación de la línea resultante, obtendrás:

$$y = \frac{m_1}{m_2}x + 1$$

Esta línea intersecará el círculo en otro punto:

Click to zoom

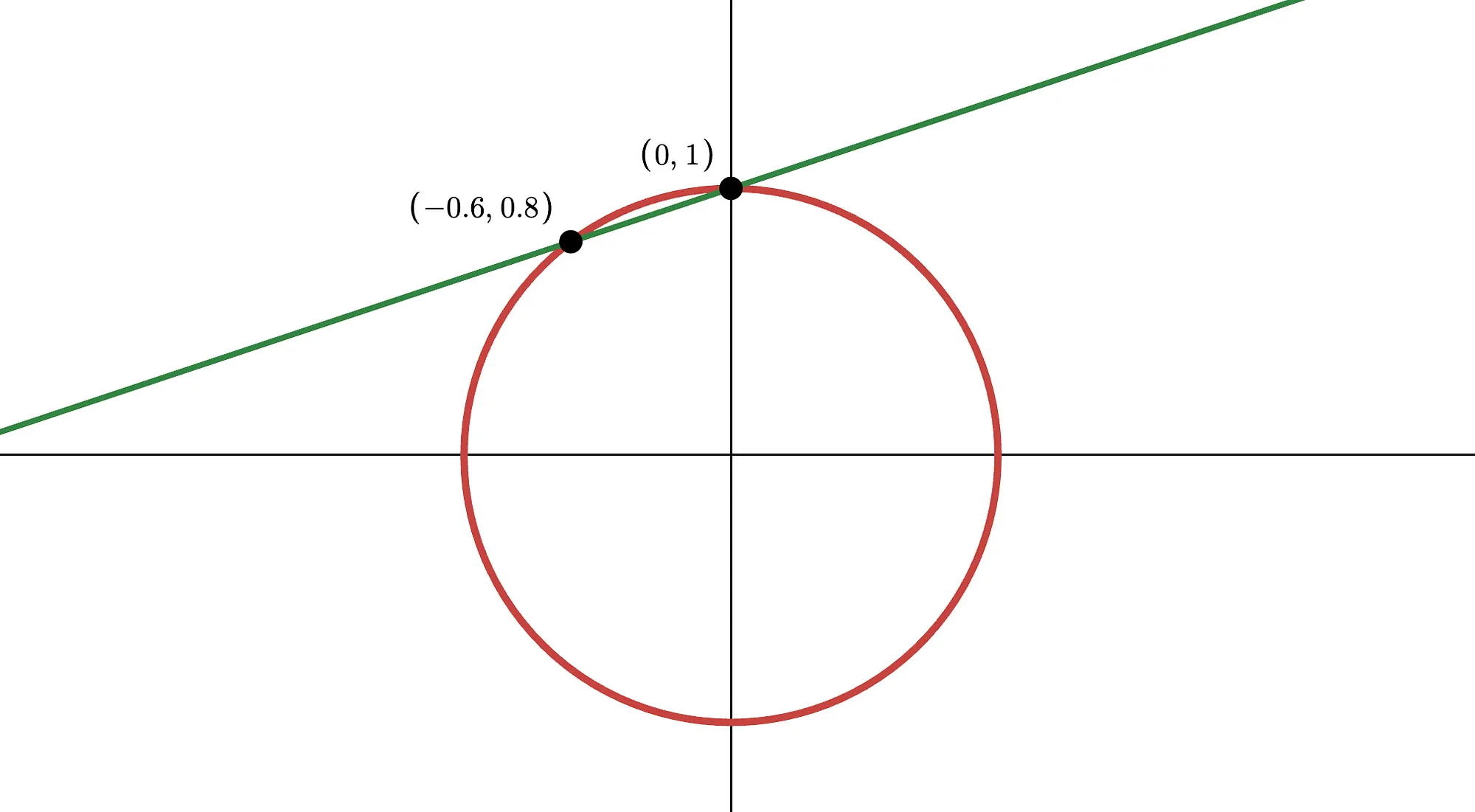
Puedes probar esto tú mismo en Desmos.

Oh, ¿qué es eso? ¡El nuevo punto es racional!

¿Fue eso una casualidad?

No, no lo fue. Sin embargo, justificar esto requiere algo de trabajo.

Conjugados de Galois

Primero necesitamos definir qué es una función racional: es una función que puede expresarse como el cociente de dos polinomios con coeficientes racionales. Nuestra línea es claramente una función racional — después de todo, ¡es un polinomio con coeficientes racionales en sí mismo!

Cuando trabajamos con estas funciones racionales, los puntos de intersección entre curvas y nuestra función racional satisfacen una condición especial.

Una condición que solo podemos entender si sabemos qué es un grupo de Galois.

Para esto, sugiero un repaso rápido sobre qué es la clausura algebraica de un campo.

Un grupo de Galois es un grupo cuyos elementos son funciones — automorfismos, para ser precisos. Solo un nombre elegante para llamar a funciones biyectivas que toman un elemento de un conjunto y lo mapean a otro elemento del mismo conjunto. "Reordenan las cosas", por así decirlo.

Pero no cualquier conjunto de automorfismos — es el conjunto de todos los automorfismos que fijan elementos en el campo base $K$ (lo que significa que actúan como la identidad), mientras reordenan elementos en la clausura algebraica $\bar{K}$. Así:

Click to zoom

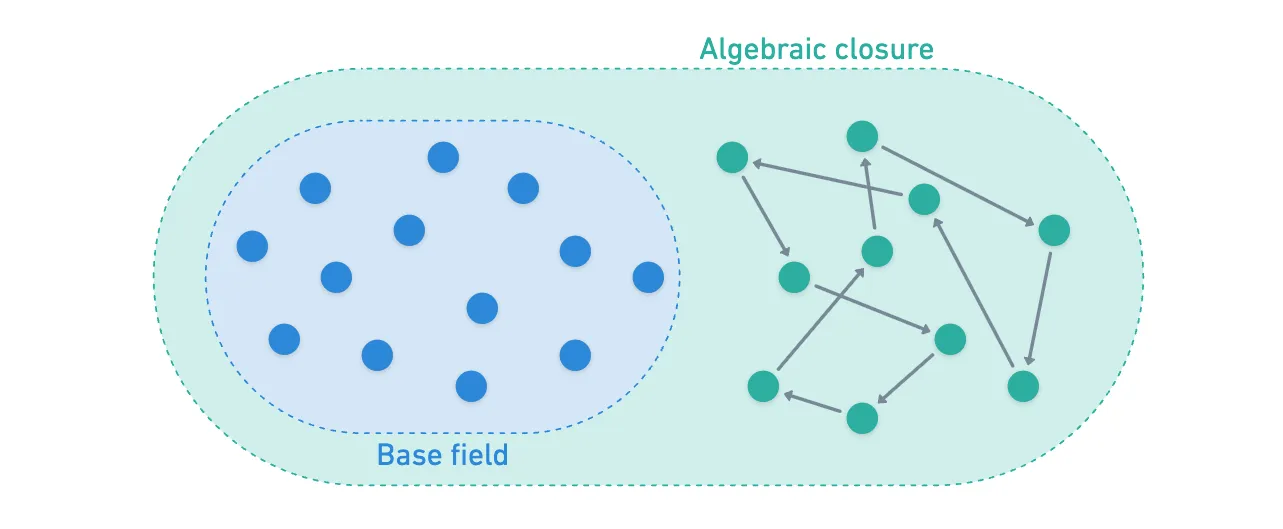
Y denotamos al grupo $\textrm{Gal}(\bar{K}/K)$.

Este es el punto donde presumo que te estás preguntando "pero Frank, ¿por qué demonios debería importarme esto?".

Aquí está el asunto: podemos demostrar que los puntos de intersección entre una curva y una función racional necesitan venir en conjugados de Galois del grupo de Galois $\textrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$ — donde $\mathbb{Q}$ son los números racionales. Esto significa que todos los puntos son o bien elementos del campo base, o bien todos pertenecen a la clausura algebraica (pero no al campo base).

O en español: o bien son todos puntos racionales, o son todos irracionales. ¡No hay término medio!

En realidad, esto no es estrictamente correcto, pero la simplificación tendrá que servir por hoy.

La definición más precisa de un conjugado de Galois es que el conjunto de puntos de intersección es invariante bajo la acción del grupo, lo que acaba significando más o menos lo que acabamos de decir.

Demostrar esto es bastante complicado. Puedes encontrar más información en libros de texto como este, pero para nuestros propósitos, creo que podemos quedarnos simplemente con la conclusión. Te dejo aquí un video divertido sobre la teoría de Galois y algunas de sus otras aplicaciones, por si acaso:

Muy bien, volvamos a la realidad. Repetiré la conclusión de esta digresión matemática:

O bien todos los puntos de intersección de una función racional y una curva son racionales, o bien todos son irracionales.

Naturalmente, en nuestro ejemplo del círculo, dado que comenzamos con un punto racional y dibujamos una función racional (línea) a través de él, se garantizaba que el otro punto de intersección fuera racional. Y lo divertido es que podemos seguir repitiendo este proceso infinitas veces.

En un proceso muy parecido a la proyección estereográfica. Por cierto, parece un método simple, pero se necesitó un genio matemático como Henri Poincaré para proponerlo. Así que ahí está.

¿Pero sabes qué? Esto no funciona con cualquier círculo. Supongamos que elegimos $R = \sqrt{2}$ en su lugar. Luego, intenta encontrar un punto racional para empezar a dibujar líneas a través. Rápidamente descubrirás que no puedes encontrar uno. Y en efecto, este círculo no tiene ningún punto racional.

Podemos probar esto más rigurosamente, pero de nuevo, ya te estoy pidiendo que me creas en un par de cosas, así que ¿qué es otro acto de fe a estas alturas?

Ya es suficiente de círculos por hoy. ¿Qué tiene que ver todo esto con las curvas elípticas?

Puntos Racionales en Curvas Elípticas

La técnica de dibujar líneas que destacamos anteriormente no debería sernos desconocida a estas alturas. Es esencialmente lo que haces durante la suma de puntos y la duplicación cuando trabajas con curvas elípticas — lo que resulta en el grupo de Mordell-Weil del que ya hemos hablado.

Aunque, cuando hablamos de él, no cuestionamos si existían puntos racionales o no, ni nos preguntamos sobre el tamaño de estos grupos — o más importante aún, si eran finitos o infinitos.

¡Y debemos poder encontrar puntos racionales, porque toda la esencia de las curvas elípticas en criptografía es trabajar con ellas sobre campos finitos!

Para ilustrar los desafíos, usemos de nuevo algunos ejemplos.

Considera la curva $y^2 = x^3 - 2x + 1$. Esta curva tiene algunos puntos racionales que puedes detectar a simple vista — por ejemplo, $P = (0,1)$. Ahora, no podemos dibujar cualquier línea, como hicimos con el círculo. Necesitamos seguir la regla de la cuerda y tangente.

Así que comencemos duplicando $P$. Necesitamos encontrar la línea tangente a la curva en dicho punto. La pendiente de dicha línea es un resultado que exploramos hace un par de artículos — y resulta ser un número racional.

Por lo tanto, la línea tangente es una función racional. Como $P$ es racional, sabemos que el otro punto de intersección también será racional. Como un reloj, $[2]P$ cae en $(1,0)$.

Click to zoom

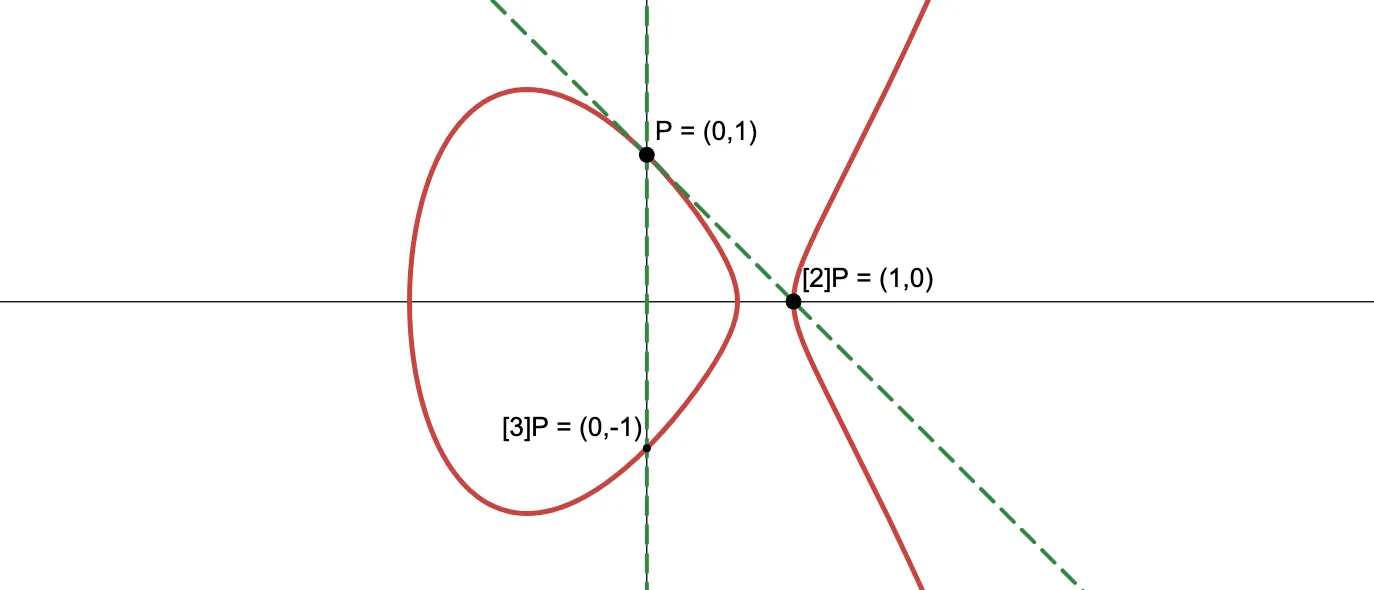
Sumar $P$ y $[2]P$ da $[3]P = (0,-1)$. Y finalmente, $[4]P = \mathcal{O}$. Este es un grupo cíclico finito de 4 puntos, ya que $[5]P = P$.

Probemos ahora con una curva diferente: $y^2 = x^3 - x + 1$. Un punto racional trivial es $P = (1,1)$, así que dibujemos de nuevo la tangente y veamos qué sucede.

Siéntete libre de probar esto tú mismo de nuevo en Desmos. Al menos hasta que te canses. Spoiler: ¡no encontrarás ningún ciclo!

¿Lo intentaste? Si lo hiciste, probablemente notaste que nuevos puntos extraños seguían apareciendo, sin repetir uno solo — todos ellos siendo puntos racionales. Podrías seguir haciendo esto para siempre y nunca encontrar un duplicado.

Lo que acabamos de encontrar es un grupo infinito de puntos racionales.

Hora de las preguntas: ¿son esos todos los puntos racionales en la curva?

Lo creas o no, esta pregunta ha mantenido despiertos a muchos matemáticos durante mucho tiempo. Y todavía no sabemos cómo responderla.

Sin embargo, tenemos pistas. Y una famosa conjetura, que no ha sido probada aún, pero que de ser cierta, nos daría herramientas para responder esta pregunta.

Rango

Para entender la conjetura, primero necesitamos introducir qué es el rango de una curva.

En los ejemplos anteriores, había algunos elementos generadores (los puntos $P$ que usamos) que producían grupos finitos, mientras que otros producían grupos infinitos. Del mismo modo, decimos que $P$ tiene un orden finito en el primer caso, o un orden infinito en el segundo.

Ahora, los grupos finitos son fáciles de describir — simplemente podemos listar todos sus elementos. Pero para grupos infinitos, al igual que para conjuntos infinitos, esto no es posible.

Así que lo que hacemos es describirlos en términos de sus generadores.

Podemos usar el concepto de presentación de grupo para esto, como notación abreviada.

Esta nueva idea nos permite reformular la pregunta que planteamos hace unos párrafos — ahora preguntamos:

¿Cuántos generadores diferentes de orden infinito necesitamos para generar todos los puntos de orden infinito en una curva elíptica?

Ese número, amigos míos, se llama el rango de una curva.

Puedes pensar en ello como el número de "dimensiones" de un grupo de curva elíptica.

De hecho, hay un teorema (el teorema de Mordell-Weil) que establece que podemos expresar el número de puntos racionales en una curva elíptica como:

$$E(\mathbb{Q}) \simeq E(\mathbb{Q})_{\textrm{tors}} \oplus \mathbb{Z}^r$$

Que traducido al dialecto humano, significa que puede expresarse como la combinación de un subconjunto finito (el grupo de torsión, que discutiremos en el próximo artículo), y otro grupo que es isomórfico a $\mathbb{Z}^r$ — siendo esa pequeña $r$ el rango de la curva.

Parece que estamos progresando, pero desafortunadamente, no es así. Porque ahora la pregunta se convierte en:

¿Cómo determinamos el rango de una curva elíptica?

¿Cómo empezamos siquiera a intentar responder eso?

Y aquí es donde se pone realmente complicado. Agárrate a tu asiento — las cosas están a punto de ponerse matemáticamente turbulentas.

La Conjetura

Ok, primero, un poco de historia.

Alrededor del año 1965, los matemáticos ingleses Bryan John Birch y Peter Swinnerton-Dyer estaban estudiando este mismo problema que ocupa nuestras mentes en este momento.

Su enfoque era simple. Tomaron un campo finito (de orden primo $p$), y luego contaron cuántas de las posibles combinaciones de $x$ e $y$ eran soluciones de alguna curva elíptica $E$. Y llamaron a este número $N_p$.

Sí, no es el tipo de enfoque riguroso que habríamos imaginado, quizás.

Y para una sola curva, lo intentaron con varios valores diferentes de $p$. Y luego, graficaron esta función:

$$f(x) = \prod_{p \leq x} \frac{N_p}{p}$$

Debo admitir que esto parece bastante... Aleatorio. Pero en un giro inesperado de los eventos, se encontraron con esta gráfica, que desde entonces se ha vuelto bastante famosa:

Click to zoom

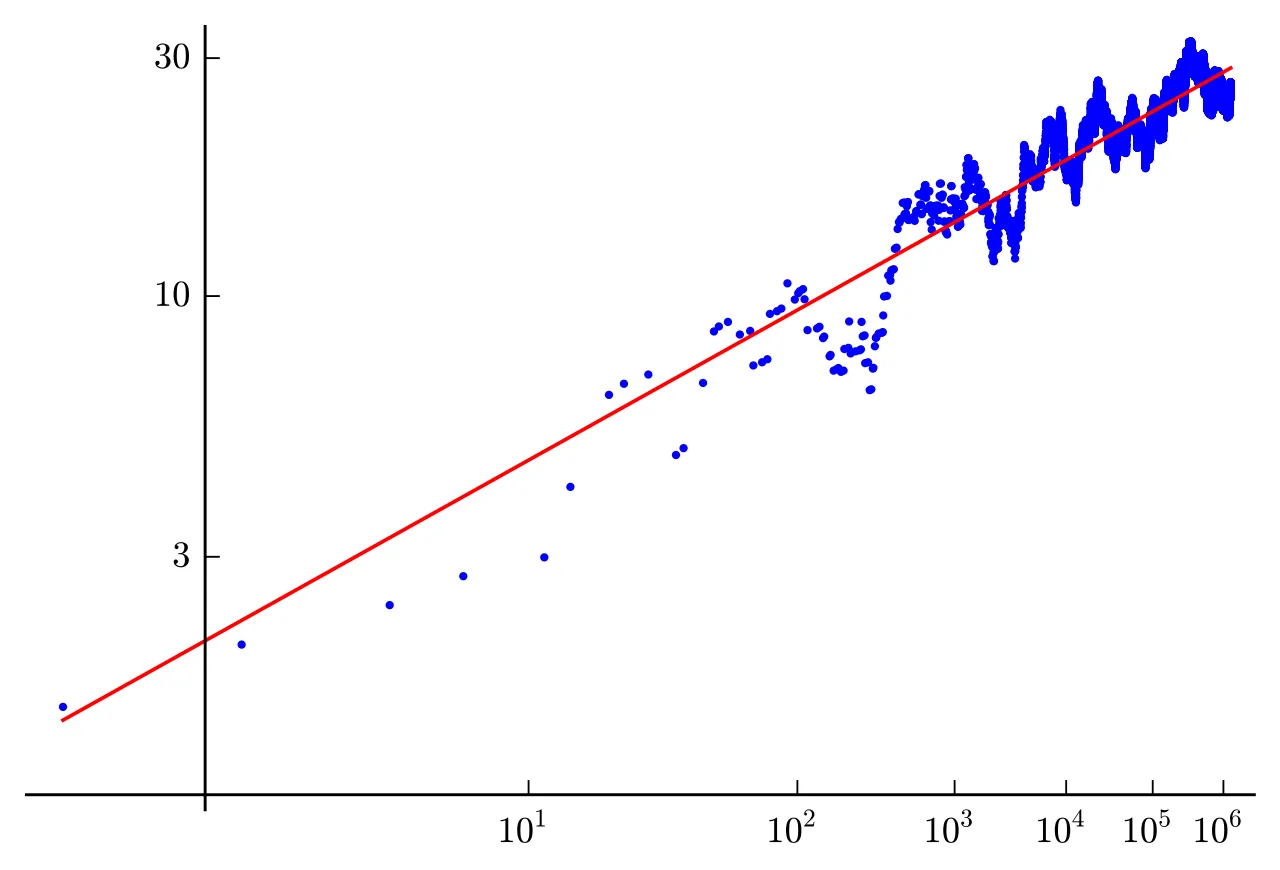
Esa línea roja que ves corresponde a la función:

$$g(x) = C.\textrm{log}(x)^r$$

Y sí, ese exponente $r$ es el rango de la curva.

Paradójicamente, otras curvas de rango conocido parecían seguir esta tendencia — lo que llevó a la pregunta: ¿sucede esto para cada curva elíptica?

Esto se conoció como la conjetura de Birch y Swinnerton-Dyer (o conjetura BSD para abreviar), y es uno de los Problemas del Milenio propuestos por el Instituto Clay de Matemáticas que sigue sin resolverse.

¡Puedes ganar 1 millón de dólares si lo resuelves!

Es una conjetura que, de ser cierta, nos permitiría conocer el rango de las curvas elípticas con total certeza. Sin embargo, la forma en que te mostré el problema es bastante inconveniente, debido a toda la cuestión de contar soluciones.

¿No podemos encontrar otra forma más conveniente de formular el problema?

Funciones L

¿L-qué?

Para transformar la conjetura en algo más manejable, tenemos que sumergirnos en el fantástico y casi místico mundo del análisis complejo.

Las funciones L son funciones de valor complejo que son bien conocidas por tener esta extraña capacidad de conectar áreas aparentemente desconectadas de las matemáticas. Por ejemplo, la hipótesis de Riemann — un problema que, de resolverse, revelaría completamente la estructura de los elusivos números primos — está formulada en términos de una función L.

La idea clave es que proporcionan una forma de estudiar analíticamente objetos aritméticos. Es un trabalenguas, lo sé.

En algún momento, los matemáticos se dieron cuenta de que la conjetura podía reformularse en una forma más elegante, utilizando estas funciones L. Realmente no soy un experto en este campo, así que solo te daré la definición y las pequeñas ideas que pude captar.

La Conjetura Refinada

Muy bien, definamos un par de cosas.

Para cada número primo $p$, primero definimos un número $a_p$ como:

$$a_p = p - N_p$$

Luego, lo usamos para definir lo que se llama un factor local:

$$L_{(p)}(E,s) = \frac{1}{1 - a_pp^{-s} + p^{1 - 2s}}$$

Donde $s$ es una variable de valor complejo.

Puedes ver que $E$ también es una entrada a la función, ya que afecta el valor $N_p$, que depende de $E$.

Finalmente, tomamos el producto de los factores locales sobre la totalidad de los números primos:

$$L(E,s) = \prod_p L_{(p)}(E,s) = \prod_p \frac{1}{1 - a_pp^{-s} + p^{1 - 2s}}$$

Esto se conoce como la función L de Hasse-Weil.

Con esto, la conjetura de Birch-Swinnerton Dyer puede reformularse como:

El rango de una curva elíptica $E$ es igual al orden de anulación de $L(E,s)$ en $s = 1$.

Intentemos desglosar eso un poco.

Cuando decimos orden de anulación, en realidad estamos hablando de cuántas veces necesitas tomar derivadas de la función antes de obtener un valor no nulo. Por ejemplo:

• Si $L(E,1) \neq 0$, el orden de anulación es $0$, y el rango es $0$.
• Si $L(E,1) = 0$, pero $L'(E,1) \neq 0$, el orden de anulación es $1$, y el rango es $1$.
• Si $L(E,1) = 0$ y $L'(E,1) = 0$, pero $L''(E,1) \neq 0$, el orden de anulación es $2$, y el rango es $2$.

Y así sucesivamente.

Lo que es bastante mágico es cómo esto codifica el rango en las derivadas. Probablemente hay una buena explicación para esto, pero por ahora, honestamente va más allá de mi comprensión actual del tema.

Las funciones L en general parecen tener la capacidad de codificar información para objetos algebraicos — valores que llamamos invariantes.

Al igual que el j-invariante que discutimos hace unos artículos.

De hecho, la conjetura BSD es un caso especial de una conjetura más moderna y de mayor alcance llamada la conjetura de Bloch-Kato, que es un intento de explicar por qué estas funciones L tienen un comportamiento tan notable.

Es un área de investigación muy críptica, misteriosa y fascinante.

Resumen

Creo que eso es más que suficiente por hoy.

Probablemente saldrás de este artículo con más preguntas que respuestas. De alguna manera, esa es la belleza de las matemáticas: todavía tenemos muchos problemas por resolver y muchos misterios por develar.

Esto también destaca lo complejas que son las curvas elípticas. Y recuerda — todo comienza con una expresión de aspecto muy inocente:

$$E: y^2 = x^3 + ax + b$$

Espero que, como mínimo, haya podido convencerte de que los puntos racionales en curvas elípticas existen, y podemos usarlos como base para construir una criptografía interesante.

Nuestro objetivo nos llevó por un camino de rareza matemática. Siempre hay más por saber, y creo que es muy importante ir tan lejos en un tema como uno encuentre práctico o divertido. A menudo es mejor enfocarse primero en el panorama general y refinar los detalles más tarde.

¡Eso es lo que funciona para mí, de todos modos!

¡Bien entonces! En el próximo artículo, continuaremos con más definiciones locas, pero con un enfoque más claro: entender los emparejamientos.

¡Nos vemos pronto!