Curvas Elípticas En Profundidad (Parte 5)

Durante nuestros encuentros anteriores, mencioné un par de veces cómo la operación de grupo para curvas elípticas (suma de puntos) se sentía un poco... Forzada. O quizás retorcida es una mejor descripción.

Como si algún gigacerebro con 200 años de conocimiento matemático la hubiera diseñado así por alguna razón mística que nuestros simples cerebros mortales no son capaces de comprender.

A estas alturas, al menos tenemos una noción de por qué las curvas elípticas podrían ser grupos atractivos. Vimos que se pueden hacer cosas interesantes y particulares con ellas — por ejemplo, cómo podemos producir twists de curvas. Este tipo de comportamientos dan a las curvas elípticas matices especiales que otros grupos pueden no exhibir.

Sin embargo, todavía tenemos esa pregunta persistente: ¿quién demonios ideó esa extraña estrategia de suma de puntos? ¿Y por qué? ¿Podríamos haberlo hecho de manera diferente?

Bueno amigos, hoy responderemos esas preguntas. Pero la maquinaria que necesitaremos para hacerlo es bastante abstracta.

Porque sí, hoy finalmente hablaremos de divisores.

Esto no solo nos dará una mejor comprensión de la operación de suma de puntos, sino que también nos abrirá el camino para definir y entender los emparejamientos.

Sin más preámbulos, ¡vamos!

Divisores

No hay muchas formas de endulzar esto. Simplemente daré la definición formal. Aquí va:

Un divisor en una curva $C$ sobre cualquier campo $K$ con clausura algebraica $\bar{K}$ es una forma de expresar un conjunto de puntos en la curva, escrito como una suma:

$$D = \sum_{P \in C(\bar{K})} n_P(P)$$

Donde $n_P$ es un entero que es distinto de cero para un número finito de puntos.

¡Te lo advertí!

Intentemos darle un poco de sentido a esto.

En primer lugar, vemos que los divisores no están restringidos a curvas elípticas. Tampoco están restringidos al campo de los enteros módulo $p$. Son una herramienta más general y tienen aplicaciones en la comprensión de otros tipos de sistemas.

En segundo lugar, nunca definimos qué es la clausura algebraica de un campo. La verdad es que no necesitamos preocuparnos demasiado por eso para nuestros propósitos. Pero para dar una descripción completa, expliquémoslo rápidamente.

La clausura algebraica de un campo $K$ se relaciona con las posibles soluciones de polinomios con coeficientes en $K$. Y aquí, puede ayudar pensar en un campo familiar: los números reales.

El polinomio $P(x) = x^2 + 1$ no tiene soluciones reales. Es decir, algunas soluciones no están en nuestro campo original. La clausura algebraica incorpora todas las posibles soluciones a polinomios con coeficientes reales — de hecho, la clausura algebraica de los números reales, ¡son los números complejos!

En el contexto de las curvas elípticas, trabajar con la clausura de nuestro campo finito tiene un propósito: añadir el punto en el infinito ($\mathcal{O}$) a la mezcla.

Eso es todo lo que nos importa — no es necesario reflexionar mucho más sobre esto. Todo lo que nos importa es que, en el contexto de las curvas elípticas, $C$ es simplemente una de esas curvas $E$, y $K = \mathbb{F}_p$. Y la clausura algebraica nos permite tener el punto en el infinito como una posible solución polinomial. Fin de la historia.

Bien, volvamos a los divisores. Aquí está la ecuación de nuevo:

$$D = \sum_{P \in C(\bar{K})} n_P(P)$$

La definición menciona que esto es un conjunto de puntos — realmente un multi-conjunto de puntos. Esta multiplicidad se expresa mediante $n_P$. Imagina que si el punto $P$ aparece "tres veces" en este conjunto, simplemente tenemos $n_P = 3$. Pero lo interesante de esta representación es que $n_P$ puede ser negativo.

Por último, la definición dice que todos los coeficientes $n_P$ son cero excepto para un número finito de puntos. En otras palabras, esto está diciendo simplemente que la suma es finita.

En definitiva, un divisor podría verse así:

$$3(P) + 2(Q) - e(\mathcal{O})$$

Vale la pena señalar que esto no es lo mismo que sumar puntos. $3(P)$ no es lo mismo que $[3]P$, que significa sumar $P$ tres veces. ¡Y el resultado de toda esa expresión no es un punto! Es un divisor.

Las cosas comenzaron un poco locas, pero logramos afirmarnos y ordenar un poco la situación. Todo está bien.

Lo que no está claro es por qué nos importan estas cosas.

Divisores y Funciones

Los divisores tienen una estrecha relación con los puntos de intersección de funciones y curvas. Y también codifican maravillosamente la multiplicidad de dichos puntos.

Toma por ejemplo una línea que interseca una curva elíptica. Ya sabemos cómo se comporta — obtendremos un total de tres puntos de intersección. Estos serán $P$, $Q$ y $-(P+Q)$.

Click to zoom

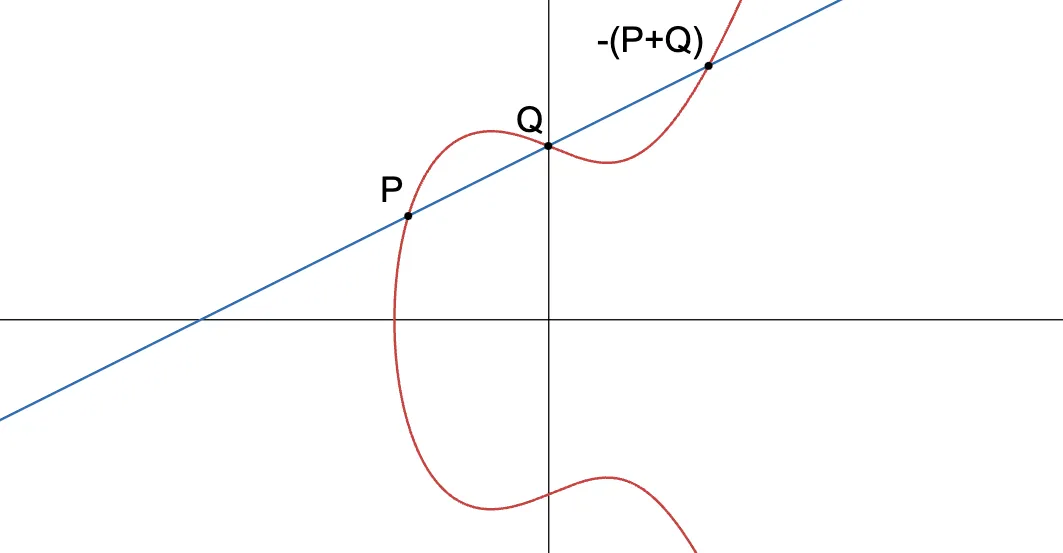
Quizás más sorprendentemente, la línea también "interseca" a $\mathcal{O}$. La razón de esto se revela al mirar las coordenadas proyectivas:

$$\frac{Y^2}{Z^2} = \frac{X^3}{Z^3} + a\frac{X}{Z} + b$$

Podemos ver que hay un polo (o singularidad, o un punto donde una función tiende a infinito, por así decirlo) en $Z = 0$, y $Z$ aparece tres veces. No debería sorprendernos que la multiplicidad de $\mathcal{O}$ sea $3$.

En definitiva, el divisor para una línea $\ell$ es:

$$(\ell) = (P) + (Q) + (-(P + Q)) - 3(\mathcal{O})$$

Si lo piensas, lo que tenemos aquí es una representación de las raíces y polos que resultan de sustituir $\ell$ en $E$. Podemos ver que las raíces tienen multiplicidades positivas, mientras que los polos tienen multiplicidades negativas.

En general, el divisor de una función $f$ se define como:

$$(f) = \sum_{P \in E(\bar{\mathbb{F}_p})} \textrm{ord}_P(f) . (P)$$

Donde $\textrm{ord}_P(f)$ representa la multiplicidad del punto $P$.

Otra cosa genial de los divisores es que podemos sumarlos. Y además, hay una traducción muy útil del álgebra entre funciones, a sus divisores:

$$(f.g) = (f) + (g)$$ $$(f/g) = (f) - (g)$$

Esto puede no parecer muy inspirador al principio. Pero piénsalo: simplemente sumar o restar divisores nos dice algo sobre los puntos de intersección de cocientes o productos de funciones con una curva. Eso es poderoso, porque puede que ni siquiera conozcamos la forma de esos cocientes o productos. Esto será muy útil muy pronto.

Divisores y Grupos

Lo que sigue es un montón de definiciones que nos llevarán en un viaje explorando la estructura de grupo de los divisores.

¡Apuesto a que no esperabas esa!

Va a ponerse un poco más complicado. Vayamos despacio.

Divisores en una Curva

Por supuesto, una curva elíptica (bueno, realmente, cualquier curva) tiene muchos divisores. Sobre los números reales, tiene infinitos, de hecho. Pero sobre campos finitos, el conjunto de divisores de una curva se vuelve finito.

Denotamos el conjunto de todos los divisores de una curva $E$ como $\textrm{Div}(E)$.

También deberíamos especificar la clausura algebraica del campo como un subíndice, pero por simplicidad, podemos ignorarlo. ¡Y además, no puedo escribir eso con caracteres unicode!

Porque podemos sumar divisores de manera bastante natural — pero no podemos multiplicarlos — el conjunto de todos los divisores en una curva forma un grupo. Las reglas son simples. La suma funciona como esperarías:

$$a(P) + b(P) = [a + b](P)$$

Y la identidad del grupo es el divisor cero: un divisor donde cada $n_P$ es cero.

Ahora es un buen momento para introducir un par de definiciones útiles:

• El grado de un divisor se define como la suma de todos sus valores $n_P$.

$$\textrm{Deg}(D) = \sum_{E(\bar{\mathbb{F}_p})} n_P$$

• El soporte de un divisor $D$ es el conjunto de todos los puntos que tienen un $n_P$ distinto de cero:

$$\textrm{supp}(D) = \{P \in E(\bar{\mathbb{F}_p}) \ : \ n_P \neq 0 \}$$

¿Cómo vamos hasta ahora? ¿Bien?

Si a estas alturas te sientes un poco perdido, te recomiendo volver a leer este artículo hasta este punto. Lo que sigue se basa en todas las ideas y definiciones anteriores.

Y se va a poner más loco. Lo siento.

Subgrupos de Divisores

Algunos divisores en el grupo general son más interesantes que otros. Y algunos de esos subconjuntos de divisores forman subgrupos propios. Veamos algunos de ellos.

El subconjunto más fácil de distinguir es el conjunto de divisores de grado cero, $\textrm{Div}^0(E)$:

$$\textrm{Div}^0(E) = \{ D \in \textrm{Div}(E) \ / \ \textrm{Deg}(D) = 0\}$$

Esto forma un subgrupo propiamente dicho, porque sumar divisores cuyo grado es cero resultará en otro divisor de grado cero, volviendo al subgrupo.

Y ¿qué podría ser atractivo de este subgrupo? Bueno, dos cosas. Una es que contiene otro subgrupo de interés.

La otra razón se hará evidente en un minuto.

Divisores Principales

Cuando $D$ es el divisor de una función $f$ (denotado $(f)$), llamamos a este divisor principal. El conjunto de todos los divisores principales se denota $\textrm{Prin}(E)$.

Los divisores principales tienen una característica definitoria: su grado es siempre cero. Este es un resultado profundo, que se remonta al teorema de Bézout, que no creo que valga la pena perseguir ahora.

Créeme en esta. Es un tema muy, muy profundo.

Sin embargo, esto plantea una pregunta: ¿es cada divisor de grado cero un divisor principal? En otras palabras, dado un divisor de grado cero $D$, ¿siempre podemos encontrar una función $f$ tal que $D = (f)$?

La respuesta es no. De nuevo, por razones que no cubriremos. Los divisores principales son de nuevo un subgrupo de los divisores de grado cero.

Sin embargo, hay una relación interesante entre estos grupos — y aquí es donde entra la segunda razón de interés para los divisores de grado cero.

El Grupo de Picard

Para establecer dicha relación, primero necesitamos definir la equivalencia de divisores.

Dos divisores $D_1$, $D_2$ son equivalentes si pueden expresarse como $D_1 = D_2 + (f)$ para alguna función $f$. Usualmente denotamos esto como $D_1 \sim D_2$.

Podemos observar algunas cosas:

• Cuando $D$ es el divisor de una función, es equivalente al divisor cero.
• Cuando elegimos algún divisor no principal $D'$, podemos generar nuevos divisores equivalentes añadiendo otros principales. Similar a cómo funciona la operación módulo.

Estas ideas naturalmente nos llevan a la estrella de todos los grupos de divisores. La crème de la crème — el grupo de clases de divisores (también llamado grupo de Picard). Se define como el grupo cociente:

$$\textrm{Pic}^0(E) = \textrm{Div}^0(E) \ / \ \textrm{Prin}(E)$$

Dicho de otra manera, es el conjunto de todos los divisores de grado cero módulo los divisores principales. La idea es que los elementos en $\textrm{Pic}^0(E)$ son irreducibles en cierto sentido, y pueden generar todo un conjunto de elementos equivalentes cuando les sumamos divisores de funciones — una clase de equivalencia.

Irreducible. Hmm. Quiero decir, sabemos cómo calcular el módulo cuando tratamos con campos finitos. Pero... ¿Cómo calculamos el módulo de un divisor?

Reducción de Divisores

Calcular el "módulo" de un divisor es más complicado que el cálculo estándar de módulo de enteros. Pero se puede hacer.

Antes de ver el proceso en acción, necesitamos un par de definiciones más:

• Un divisor es efectivo si cada $n_P$ es mayor que cero. ¡En $\textrm{Div}^0(E)$, hay un único divisor efectivo: el divisor cero!
• Debido a eso, podemos definir la parte efectiva de un divisor, definida como:

$$\epsilon(D) = \sum_{P \ / \ n_P \geq 0} n_P(P)$$

• El tamaño de un divisor es el grado de su parte efectiva.

Equipados con estos nuevos conceptos, saltemos directamente a cómo funciona la reducción de divisores.

Considera un divisor $D = (P_1) + ... + (P_9) - 9(\mathcal{O})$, de tamaño $9$. Este es claramente un elemento de $\textrm{Div}^0(E)$ — pero queremos encontrar su elemento equivalente (representativo de la clase de equivalencia) en $\textrm{Pic}^0(E)$.

Lo que hacemos ahora es interpolar los puntos $P_i$. Debe notarse que todos estos puntos están en la curva $E$.

Como referencia, puedes consultar mi artículo sobre polinomios.

La interpolación nos dará esta función:

$$\ell_8: y = \sum_{k=0}^8 a_kx^k$$

Ahora, si sustituimos esta función en $E$, obtendremos un polinomio de grado (como máximo) $16$, debido al término $y^2$ en $E$. Este polinomio tendrá entonces $16$ raíces.

Estas raíces son los puntos de intersección entre $\ell_8$ y $E$. Pero observa que los nueve puntos $P_i$ también son puntos de intersección — también pertenecen tanto a $\ell_8$ como a $E$. Esto significa que a través de este proceso, obtenemos el conocimiento de un total de siete nuevos puntos de intersección.

¡Bien! Usemos esta información para escribir el divisor de $\ell_8$. Podemos separarlo como:

$$(\ell_8) = \sum_{i=1}^9 (P_i) + \sum_{j=1}^7 (P'_j) - 16(\mathcal{O})$$

Y mira lo que sucede después de reorganizar un poco esa ecuación:

$$\sum_{i=1}^9 (P_i) - 9(\mathcal{O}) = \sum_{j=1}^7 (P'_j) - 7(\mathcal{O}) - (\ell_8)$$

¿Ves lo que pasó? En el lado izquierdo, tenemos nuestro divisor original $D$. Y en el derecho, tenemos el divisor de una función $(\ell_8)$, y un nuevo divisor cuyo tamaño es dos menos que $D$. Llamémoslo $D'$.

La diferencia entre $D$ y $D'$ es un divisor de función. ¿Sabes lo que eso significa? ¡Que $D$ y $D'$ son equivalentes!

Podemos seguir repitiendo este proceso una y otra vez, usando los puntos del nuevo divisor para la interpolación. Hasta... ¿Cuándo? ¿Cuándo nos detenemos? ¿Cuándo obtenemos un divisor irreducible?

Si intentas esto tú mismo, encontrarás que puedes llegar a un divisor de tamaño uno de la forma $(P) - (\mathcal{O})$.

Eso es todo lo que puedes hacer. En resumen, cada punto en la curva representa una clase de equivalencia.

Esto no es coincidencia. De hecho, es consecuencia de un teorema importante, llamado el teorema de Riemann-Roch — uno de los resultados más fundamentales en una rama de las matemáticas llamada geometría algebraica.

La geometría algebraica es un tema que me gustaría abordar en algún artículo futuro. No creo que debamos profundizar más. Aun así, una pequeña explicación de qué trata el teorema podría ayudar.

En pocas palabras, cada curva tiene una propiedad fundamental llamada su género. Tiene que ver con el número de agujeros en la superficie representada por una curva — que son las superficies formadas por una curva cuando se ve sobre los números complejos. Las curvas elípticas forman una especie de forma de dona — y, por lo tanto, tienen género $1$.

Es algo difícil de visualizar. Este post podría ayudar.

El teorema de Riemann-Roch nos dice que cualquier divisor $D$ en una curva elíptica, será equivalente a otro divisor $D'$ cuyo tamaño es a lo sumo $g$, donde $g$ es el género de la curva. En el caso de las curvas elípticas, $g = 1$. En consecuencia, cualquier divisor de tamaño mayor que $1$ puede reducirse.

No sé tú, pero encuentro este tipo de interacciones nada menos que mágicas. Muestran cómo diferentes ramas de las matemáticas están íntimamente entrelazadas, permitiéndonos mirar el mismo problema a través de diferentes lentes, y a veces revelando patrones ocultos intrincados.

Muy bien. Quizás me emocioné demasiado ahí. Lo siento.

Puede que me haya desviado un poco de nuestro objetivo principal: explicar por qué la suma de puntos funciona como lo hace. Es hora de volver a eso, usando nuestro conocimiento recién aprendido sobre divisores.

El Grupo de Mordell-Weil

Uno de los resultados clave que encontramos es que cualquier divisor de una curva elíptica puede reducirse a algo de la forma $(P) - (\mathcal{O})$. De hecho, hay una correspondencia uno a uno entre los puntos en la curva y los divisores irreducibles de esta forma.

En otras palabras: hay un isomorfismo entre el grupo de puntos en nuestra curva elíptica y el grupo de Picard ($\textrm{Pic}^0(E)$). Y la función en sí es bastante simple: mapea un punto $P$ a la clase de divisor de $(P) - (\mathcal{O})$.

Para un minuto para tratar de realmente absorber eso.

Puede que no sea evidente al principio. Lo que esto significa es que nuestra regla de aspecto elegante para sumar puntos en una curva elíptica (la ley de grupo), puede traducirse en operaciones en el grupo de Picard.

Así es cómo:

• Toma dos puntos $P$ y $Q$ en la curva
• Mapéalos a sus clases de divisor correspondientes, que son $(P) - (\mathcal{O})$ y $(Q) - (\mathcal{O})$.
• Suma estas clases de divisor, resultando en $D = (P) + (Q) - 2(\mathcal{O})$.

Ahora, esta no es la forma estándar en el grupo de Picard — el divisor es reducible. ¿Cómo lo reducimos?

Dibujemos una línea a través de $P$ y $Q$. Ésta interseca la curva en un tercer punto, que ya sabemos que va a ser $-(P+Q)$. El divisor de esta línea $\ell$ es por supuesto:

$$(\ell) = (P) + (Q) + (-(P+Q)) - 3(\mathcal{O})$$

Este es un divisor principal, porque $\ell$ es una función. Intentemos restarlo de $D$:

$$D - (\ell) = -(-(P+Q)) + (\mathcal{O})$$

¡Interesante! Esto significa que $D$ es equivalente al divisor en el lado derecho. Todo lo que queda es mapear esto a la forma $(P) - (\mathcal{O})$. Para esto, necesitamos hacer algo parecido a la negación.

Intentemos usar una línea vertical que pase por $-(P + Q)$. Es una función $v$ con este divisor:

$$(v) = (P+Q) + (-(P+Q)) - 2(\mathcal{O})$$

Y aquí es donde ocurre la magia. Sumemos eso a nuestro resultado anterior:

$$D - (\ell) + (v) = (P + Q) - (\mathcal{O})$$

Et voilà! Solo necesitamos usar nuestro isomorfismo (bueno, su inverso) para mapear de vuelta a puntos de curva elíptica, obteniendo el familiar $P+Q$.

Analicemos brevemente lo que acaba de ocurrir. Todo lo que hicimos fue mapear nuestros puntos originales a divisores, y luego sumarlos. Pero los sumamos en el grupo de Picard — y sabemos que podemos reducir este resultado a un divisor equivalente.

El broche de oro es el hecho de que la reducción se ve exactamente como nuestra extraña regla de cuerda y tangente!

Alucinante. Simplemente fenomenal.

Porque ahora, nuestra regla de suma de puntos parece aparecer naturalmente cuando trabajamos con el grupo de Picard.

No es una invención loca. Es solo una consecuencia de aprender a hablar el lenguaje de los divisores, resultando en este proceso de suma y reducción, que es la ley de grupo para lo que se llama el grupo de Mordell-Weil.

Bastante bueno, ¿no?

Multiplicación, Revisitada

Para redondear las cosas, quiero mirar la multiplicación de puntos desde la perspectiva del grupo de Mordell-Weil.

Supongamos que queremos calcular $[4]P$, dado algún punto $P$ en la curva. Hay dos maneras de hacer esto: o bien sumar $P$ a sí mismo 4 veces, o calcular $[2]P$ primero, y luego duplicar ese resultado.

No es inmediatamente claro que ambas operaciones den el mismo resultado. Pero ahora, podemos usar el grupo de Picard para inspeccionar ambos enfoques. Comenzamos con el divisor $(P) - (\mathcal{O})$. Duplicar esta clase de divisor produce:

$$D = 2(P) - 2(\mathcal{O})$$

Como este divisor tiene tamaño $2$, sabemos que es reducible. Mismo enfoque que antes — restamos el divisor de la línea tangente a $P$, y sumamos el divisor de la línea vertical que pasa por el tercer punto de intersección. Resolviendo las matemáticas, esto simplemente produce:

$$D - (\ell) + (v) = ([2]P) - (\mathcal{O})$$

Es en este punto que podemos tomar cualquiera de las dos rutas:

• Una opción es duplicar $[2]P$. Por la misma lógica, podemos encontrar el divisor correspondiente, que es $2([2]P) - 2(\mathcal{O})$. Llamemos a esto $D_1$.
• La otra es sumar $P$ dos veces más. Esto produce $([2]P) + 2(P) - 3(\mathcal{O})$. A este resultado, lo llamaremos $D_2$.

Si podemos mostrar que estos dos divisores son equivalentes, entonces ambos resultados serán efectivamente el mismo. Y realmente, es tan fácil como calcular su diferencia:

$$D_2 - D_1 = 2(P) - ([2]P) - (\mathcal{O})$$

Para interpretar fácilmente este resultado, realizaré uno de esos pequeños trucos mágicos en matemáticas: sumar y restar $(-[2]P)$, y luego también sumar y restar $2(\mathcal{O})$.

Es lo mismo que sumar cero, así que está perfectamente bien.

Déjame escribir el resultado para ti:

$$D_2 - D_1 = 2(P) + (-[2]P) - 3(\mathcal{O}) - (-[2]P) - ([2]P) + 2(\mathcal{O})$$

¡Ajá! Se está volviendo más claro, ¿no? Sí, la diferencia entre $D_2$ y $D_1$ es exactamente:

$$D_2 - D_1 = (\ell) - (v)$$

Dos divisores principales. Lo que significa, amigos míos, que estos divisores son equivalentes. Ambas operaciones se reducen al mismo valor en el grupo de Picard. ¿No es fantástico?

Por supuesto, podemos plantear un argumento similar para cualquier número $n$ — no hay nada especial en $4$. El mecanismo es exactamente el mismo, aunque podría tomar un poco más de trabajo.

Y probablemente hay una forma de mostrar esto por inducción de todos modos. No lo he intentado, ¡pero podría ser un ejercicio divertido!

¡Ahí lo tienes! Ahora podemos decir con confianza que la regla de duplicar y sumar resultará en el mismo punto que la suma de puntos repetida.

Resumen

Si has llegado hasta aquí, solo puedo agradecerte por quedarte conmigo a través de esta jungla algebraica.

La cantidad de maquinaria matemática que podemos encontrar al echar un vistazo a lo que hay detrás de algo de aspecto tan inocente como la regla de cuerda y tangente es simplemente alucinante. Y parece justo decir que estamos bastante adentrados en esta jungla — pero te sorprendería lo mucho que falta - estamos apenas rascando la superficie.

No te asustes — de todas formas, estamos muy por encima del punto de "comprensión superficial". Pero hay mucho, mucho más en lo que profundizar.

Lo importante es que hemos construido una base sólida sobre divisores. Creo que hemos cubierto suficiente por hoy, al menos.

Pero no te pongas demasiado cómodo — pondremos los divisores a buen uso en los próximos artículos, donde exploraremos los emparejamientos. ¡Se vienen cosas interesantes!

Antes de llegar allí, hay algunas cosas más que quiero decir sobre los grupos de curvas elípticas. Así que ese será nuestro próximo destino. Nos vemos pronto.