Curvas Elípticas En Profundidad (Parte 4)

Hemos cubierto bastantes cosas hasta ahora, así que creo que un repaso rápido será útil.  - La serie comenzó con una mirada a las curvas elípticas sobre $\mathbb{R}^2$ — lo que ahora llamamos espacio afín. Las curvas definidas sobre este espacio se llaman curvas afines.

• Luego introdujimos una operación sobre estas curvas, bautizada como suma de puntos. Y requeríamos precisión, así que nos movimos a curvas definidas sobre campos finitos.
• Por último, exploramos la estructura de grupo de las curvas elípticas, inducida por la operación de suma de puntos que definimos anteriormente.

Estaría completamente bien si la serie terminara aquí. Es posible crear algoritmos muy útiles con el conocimiento que hemos adquirido hasta ahora. No hay necesidad de adentrarse más en la madriguera del conejo.

Pero si has llegado hasta aquí, probablemente quieras más. Y ciertamente, hay mucho más por saber.

Nuestro viaje continúa con funciones. Esto desbloqueará posibilidades muy interesantes y poderosas. ¡Sigamos!

Funciones

Aunque la mayoría de ustedes probablemente sepan qué es una función, creo que vale la pena dar una definición de todos modos. Una función o mapa es como una caja que toma una entrada y devuelve una salida. Y lo hace de manera determinística: cada vez que pasamos la misma entrada a través de la función, obtenemos exactamente la misma salida — sin sorpresas.

Click to zoom

Por supuesto, hay definiciones más rigurosas por ahí, pero no necesitamos detenernos demasiado en los detalles ahora.

Cuando pensamos en una función, generalmente imaginamos algo como $f(x) = x^2$. Aquí, $x$ representa la entrada, y el $x^2$ calculado es la salida. Y más a menudo que no, imaginamos estos valores como números.

¡Pero no necesitan ser números!

Las entradas pueden pertenecer a cualquier conjunto, llamado dominio de la función, y las salidas pertenecen a otro conjunto, llamado su rango (o a veces también llamado codominio).

Las funciones también se llaman mapas, por la forma en que mapean cada entrada en el dominio a un valor en el rango.

Entonces, ¿qué tal si en lugar de números, intentamos usar grupos como esos conjuntos?

Mapas sobre Grupos

Los grupos, como ya sabemos, son estructuras que resultan de la combinación de un conjunto y una operación binaria. Hay formas inteligentes de definir diferentes mapas que involucren grupos, usando solo este conocimiento.

Por ejemplo, una relación muy simple sería la siguiente:

$$f: \mathbb{Z}_+ \rightarrow \mathbb{G} \ / \ f(x) = [x]G$$

Esta es una función que mapea cada entero positivo a un elemento de grupo de curva elíptica.

Por supuesto, si el grupo es finito, entonces algunos enteros tendrán el mismo valor funcional. Formalmente, esto significa que la función no es inyectiva: una función es inyectiva si cada elemento en el dominio se mapea a un elemento único en el rango. Volveremos a esto en un minuto.

Click to zoom

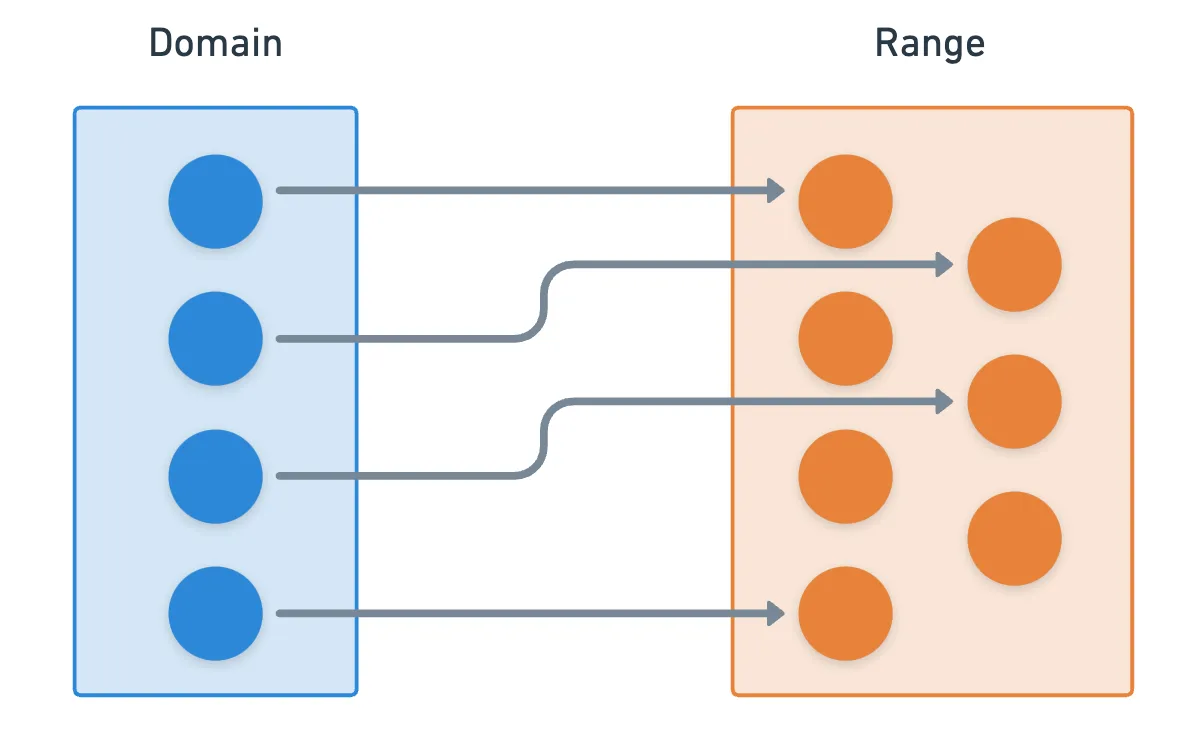
Vamos un paso más allá. Nada realmente nos impide tener una función donde tanto el dominio como el rango sean grupos.

No hay nada muy especial en esto. Una función de algún grupo $G$ a otro grupo $H$ simplemente mapea cada elemento de $G$ en $H$, y podría haber una miríada de relaciones de este tipo. Pero, ¿qué pasaría si de alguna manera lográramos preservar algunas propiedades importantes?

Seré un poco más preciso. Si el grupo $\mathbb{G}$ tiene alguna operación denotada por $\cdot$, y $\mathbb{H}$ tiene otra operación $*$, ¿no sería genial si un mapa entre $\mathbb{G}$ y $\mathbb{H}$ pudiera mantener algún tipo de relación entre estas operaciones?

Las operaciones no tienen que ser diferentes, realmente. Pero en el caso más general, lo serán.

Esto nos lleva a uno de los conceptos más importantes en la teoría de grupos: los homomorfismos. Un homomorfismo es una función que preserva la estructura del grupo. Lo que esto significa es que para cualquier par de elementos $a$ y $b$ en $\mathbb{G}$, tenemos:

$$f(a \cdot b) = f(a) * f(b)$$

Esto puede parecer poco inspirador, pero en realidad es una propiedad increíblemente poderosa. Cuando trabajamos con homomorfismos, el orden de las operaciones no importa: podemos combinar elementos y luego aplicar la función, o aplicar la función a cada elemento y luego combinarlos.

Por ejemplo, la primera función que vimos como ejemplo resulta ser un homomorfismo.

Nuevamente, volveremos a esta idea más adelante. Por ahora, solo estamos acumulando definiciones importantes. ¡Ten un poco de paciencia!

Isomorfismos

Hace un par de párrafos, hablamos de funciones inyectivas. Hay otra propiedad similar de las funciones que también necesitamos entender, llamada sobreyectividad.

Click to zoom

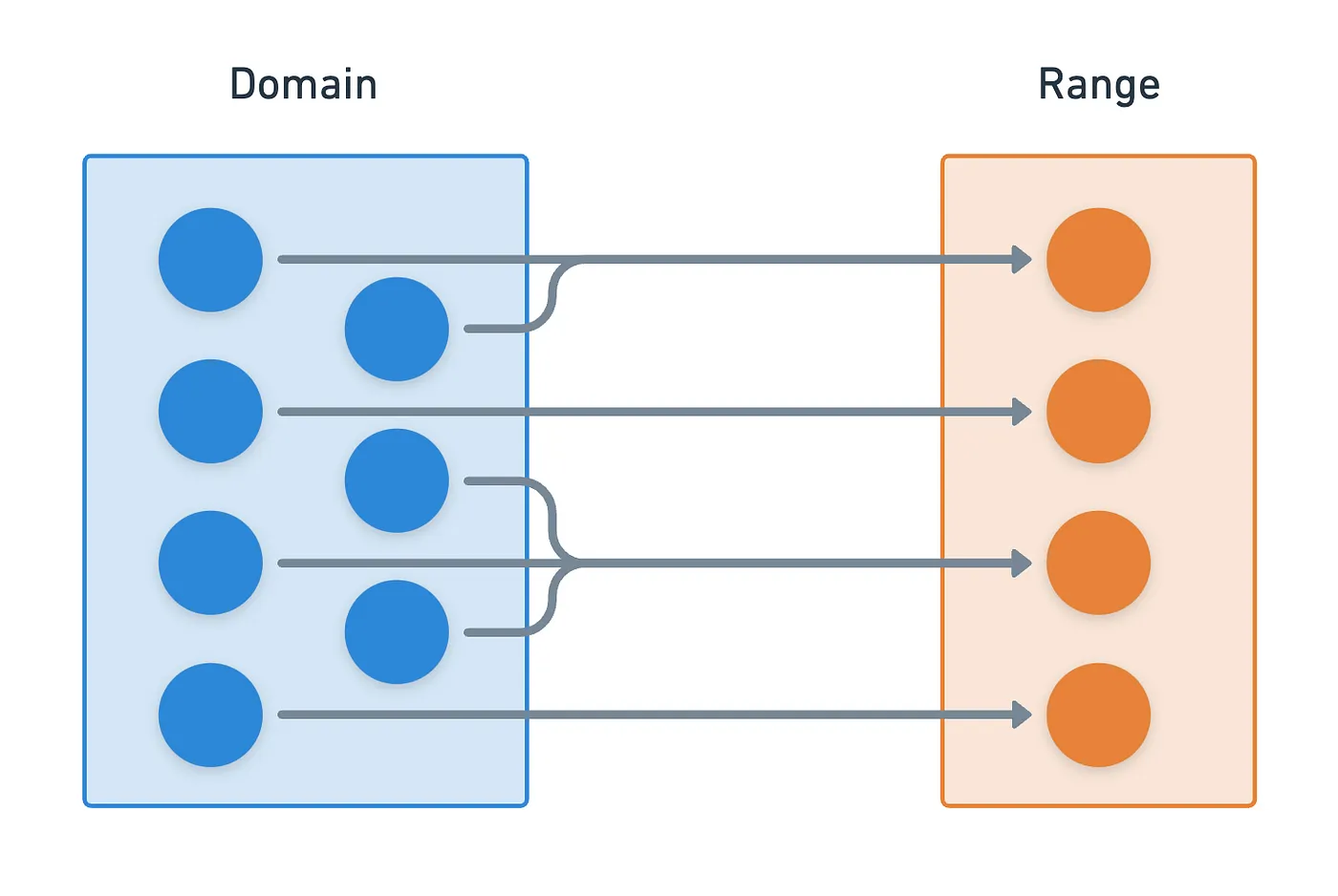
La sobreyectividad por sí sola no es tan atractiva (aunque puede ser útil en el contexto adecuado). Las cosas se ponen realmente interesantes cuando combinamos inyectividad y sobreyectividad.

En términos simples: la inyectividad garantiza que cada elemento del dominio se mapea a un elemento único en el rango, y la sobreyectividad garantiza que no hay elementos no utilizados en el rango. Esto conduce a algo fantástico: una correspondencia uno a uno. Esto normalmente se llama biyección.

Además, cuando un homomorfismo resulta ser una biyección, recibe un nombre especial: un isomorfismo. Es una correspondencia uno a uno que también preserva la estructura del grupo — una correspondencia "perfecta", por así decirlo.

Cuando existe un isomorfismo entre dos grupos (decimos que son isomorfos), lo que realmente sucede es que son el mismo grupo disfrazado. Si sabes lo que sucede en un grupo, automáticamente sabes lo que sucede en el otro — el isomorfismo te da una forma de traducir resultados de un grupo a otro.

Dato curioso: cada grupo cíclico de orden $q$ es isomórfico al grupo aditivo de enteros módulo $q$.

Ahora sí estamos hablando. Esta herramienta es realmente interesante. Veamos un ejemplo simple. Considera estas dos curvas sobre $\mathbb{F}_{17}$:

• $E_1: y^2 = x^3 + 2x + 1$
• $E_2: y^2 = x^3 + 15x + 4$

A primera vista, estas curvas se ven claramente diferentes. Ahora, observa esta función simple:

$$f: E_1 \rightarrow E_2 \ / \ f(x,y) = (2x, 13y)$$

Primero queremos verificar que, para cualquier punto $(x, y)$ que satisfaga $E_1$, obtenemos un punto que pertenece a $E_2$ después de aplicar $f$. Esto es bastante sencillo:

• Primero, sustituimos $(2x, 13y)$ en $E_2$. Esto produce $4y^2 = 4x^3 + 8x + 4$, después de la reducción módulo $17$.
• Ahora multiplicamos todo por el inverso modular de $4$, que es $13$ en $\mathbb{F}_{17}$. Después de la simplificación módulo $17$, obtenemos $y^2 = x^3 + 2x + 1$.

¡Esa es exactamente la expresión para $E_1$! Esto es genial — significa que los puntos $(2x, 13y)$ realmente satisfacen $E_2$, porque llegamos a una igualdad que sabemos que es válida.

A continuación, necesitamos verificar que $f$ es de hecho un isomorfismo. Comprobar que es tanto inyectiva como sobreyectiva es fácil — ¡te lo dejo como ejercicio!

Sobre la preservación de la estructura del grupo, digamos simplemente que $f$ se comporta bien con la ley del grupo. Podríamos entrar en más detalles en artículos futuros.

¡Así que ahí lo tienes! Dos curvas aparentemente diferentes que resultan ser isomórficas — comportándose así como la misma curva.

De nuestro ejemplo anterior, surge una pregunta interesante de manera bastante natural, especialmente en el contexto de curvas sobre campos finitos: ¿podemos siempre encontrar isomorfismos entre curvas?

Claramente, hay algo que decir sobre el orden del grupo. Dos grupos con diferentes tamaños no pueden ser isomórficos, ya que un homomorfismo entre ellos no sería inyectivo o no sería sobreyectivo.

Pero incluso cuando tenemos dos curvas del mismo orden, pueden no ser isomórficas. ¿Cómo evaluamos esto? Aquí entra el j-invariante.

El j-invariante

El j-invariante tiene una historia fascinante arraigada en el análisis complejo, que quizás sea una madriguera demasiado profunda para adentrarnos ahora mismo.

Lo crucial es que el j-invariante captura la forma esencial de una curva elíptica. Dos curvas pueden parecer diferentes a primera vista, pero si tienen el mismo j-invariante, en realidad son la misma curva (a través de un isomorfismo, por supuesto).

Para una curva en forma de Weierstrass ($y^2 = x^3 + ax + b$), el j-invariante se calcula como:

$$j = 1728.\frac{4a^3}{4a^3 + 27b^2}$$

Sí, lo sé. Esta fórmula parece surgir de la nada. Pero en realidad es una destilación de un par de siglos de matemáticas profundas en una sola expresión.

Podríamos profundizar más en este tema más adelante. Con suerte. Por ahora, solo piensa en el j-invariante como una huella digital para curvas elípticas — cada curva esencialmente diferente tiene su propio j-invariante único.

Todo está bien y bonito con el j-invariante. Dos curvas que comparten este mismo valor característico serán de hecho isomórficas, pero eso es solo parte de la historia. Lo que no mencioné es dónde están definidas esas curvas isomórficas.

Me explico. Dos curvas pueden compartir el mismo j-invariante, pero cuando intentamos encontrar un isomorfismo entre ellas, podemos ser incapaces de encontrarlo. No importa qué agreguemos o multipliquemos a las coordenadas de los puntos, encontrar un isomorfismo puede resultar una tarea imposiblemente difícil.

Eso es, si nos limitamos a los campos finitos tal como los conocemos hasta ahora.

Extensiones de Campo

Hemos estado trabajando con campos finitos como $\mathbb{F}_p$. A veces, estos campos no son "lo suficientemente grandes" para que encontremos esos escurridizos isomorfismos que buscamos.

Así como podemos extender los números reales a los números complejos simplemente añadiendo $i$ a la mezcla, también podemos extender campos finitos añadiendo nuevos elementos.

Por ejemplo, toma $\mathbb{F}_{17}$. Supongamos que quisiéramos encontrar la raíz cuadrada de $2$ en este campo — esto es, un número que satisface $x^2 \equiv 2 (\textrm{mod} \ 17)$. Puedes comprobar fácilmente que ningún elemento en $\mathbb{F}_{17}$ satisface esta relación.

Pero podemos crear un campo más grande que contenga tal elemento. Si añadimos un elemento $i$ tal que $i^2 + 1 = 0$, entonces una solución aparece casi mágicamente. Los números $7i$ y $-7i$ son las raíces cuadradas de $2$. Puedes comprobarlo tú mismo.

En este contexto, llamamos a $\mathbb{F}_{17}$ el campo base, y al nuevo campo con $i$ se le llama una extensión de campo. En este caso, se escribe como $\mathbb{F}_{17}^2$.

Contiene todos los elementos de $\mathbb{F}_{17}$, más algunos nuevos — un total de $17^2 = 289$ elementos, para ser precisos.

Es realmente como la extensión compleja de $\mathbb{F}_{17}$. Pero no estamos limitados a definir $i$ de la manera que lo hicimos antes, lo que significa que ¡hay infinitas posibles extensiones de campo!

Sobre estas extensiones de campo, ahora podemos encontrar esos elusivos isomorfismos profetizados por el j-invariante. Lo que nos lleva a nuestro siguiente tema...

Twists

Cuando dos curvas son isomórficas cuando se ven sobre algún campo más grande (una extensión de campo), decimos que estas curvas son twists una de la otra.

El tipo más común de twist se llama twist cuadrático. Estas son muy fáciles de construir: simplemente multiplicas el término $y^2$ por un no-cuadrado $d$ (es decir, un número que no tiene raíz cuadrada en el campo):

$$E': dy^2 = x^3 + ax + b$$

Observa que esta nueva curva tiene el mismo j-invariante que la curva original $E$. Por lo tanto, debería existir un isomorfismo entre $E$ y $E'$ — pero el hecho de que $d$ no sea un cuadrado hace imposible encontrarlo sobre el campo base.

Como nota al margen, ¡si $d$ es un cuadrado, entonces las curvas son isomórficas sobre el campo base!

Esto puede parecer nada más que una curiosidad, pero los twists son en realidad una herramienta bastante importante en criptografía.

En ciertas situaciones, podríamos encontrarnos en la necesidad de realizar cálculos de curvas elípticas sobre extensiones de campo. Estos son costosos (computacionalmente) en comparación con las operaciones sobre el campo base. Y en criptografía, la velocidad vende.

Si puedes encontrar un twist de la curva que pueda operar sobre el campo base, puedes realizar cálculos allí, y luego mapear de vuelta a la curva (grupo) original a través de su isomorfismo de conexión. ¡Bastante bueno!

Esto es especialmente útil cuando se trata de Emparejamientos. Hablaremos de ellos más adelante en la serie.

Pero no es tan simple como suena. Nada lo es. Encontrar tal twist puede no ser una tarea fácil. Además, podríamos tropezar con una twist débil — un grupo cuya estructura es fácil de descifrar. Es por esto que a menudo también requerimos curvas que tengan "torsiones seguras". Un atacante que no puede romper tu curva podría intentar moverse a una twist más débil, con la esperanza de romper tu seguridad. ¡Así que supongo que la existencia de torsiones es una especie de bendición y maldición!

Isogenias

¡Uf, ya estamos bastante adentrados en esto!

Ya hemos hablado de isomorfismos entre curvas — mapas biyectivos que preservan la estructura del grupo. Para algunas aplicaciones, son exactamente lo que necesitamos. Pero a veces, puede que no necesitemos toda la fuerza de una correspondencia perfecta.

Tal vez algo ligeramente más flexible es justo lo suficiente. ¿Quizás un homomorfismo — pero casi cualquier homomorfismo? Además de tratar de preservar la estructura del grupo, ¿hay otras propiedades que podríamos querer? Aquí es donde entran en juego las isogenias.

Una isogenia es un mapa racional entre curvas elípticas, que también es un homomorfismo de grupo.

No nos preocupemos demasiado por la parte del mapa racional, y expresemos esta idea en términos simples. Además de preservar la estructura del grupo, las isogenias tienen otra propiedad notable: preservan el elemento identidad ($\mathcal{O}$). Esto significa que mapean el $\mathcal{O}$ en el dominio al $\mathcal{O}$ en el rango (siendo ambos grupos de curvas elípticas).

El ejemplo más simple de una isogenia es el mapa de multiplicación por n, $P \mapsto [n]P$. ¡Puedes verificar directamente que se cumple la condición de preservación de identidad!

De hecho, este mapa conduce al concepto de puntos de r-torsión: puntos $P$ tales que $[r]P = \mathcal{O}$. El conjunto de todos los puntos de r-torsión forma un grupo, denotado $E[r]$. Hablaremos de esto en próximos posts.

Cuando se juntan, estas dos condiciones también aseguran que suceda algo más: el núcleo de una isogenia debe ser finito. El núcleo de un homomorfismo $f: E_1 \rightarrow E_2$ es simplemente el conjunto de todas las entradas que se mapean al elemento identidad $\mathcal{O}$ en $E_2$. Es el concepto análogo a las raíces.

Para referencia y pruebas rigurosas, sugiero consultar Algebraic Geometry de Hartshorne, Capítulo II. La Proposición 6.8 muestra la prueba de esto. Y estoy dispuesto a apostar que esto es mucho más de lo que esperabas cuando comenzaste a leer esto.

También, si te sientes especialmente aventurero, te sugiero leer esto.

En términos simples: una isogenia solo puede colapsar un número finito de puntos a $\mathcal{O}$. O dicho de otra manera, solo un número finito de puntos pueden mapearse a $\mathcal{O}$.

Este es un tema muy, muy profundo. Para ser justos, esto apenas rasca la superficie de lo que hay que saber, y la mayoría de los libros de texto en esta área son muy técnicos y densos.

Y todavía tengo mucho que aprender yo mismo.

Lo que diré es que las isogenias tienen muchas aplicaciones en criptografía. Una de las aplicaciones más interesantes (y recientes) se relaciona con la dificultad de encontrar isogenias entre curvas.

Ah, porque las isogenias pueden ser compuestas, lo que lleva al concepto de grafos de isogenia. De hecho, la dificultad de calcular isogenias se asemeja a encontrar un "camino oculto" en un grafo de isogenia.

Algunos métodos basados en isogenias incluso fueron propuestos como posibles candidatos para algoritmos de Criptografía Post-Cuántica (PQC) — un ejemplo de ello es el Intercambio de Claves Diffie-Hellman de Isogenia Supersingular. Tristemente, el método fue recientemente descifrado — pero fue debido a la estructura específica del esquema.

Reconozco que esta sección está bastante simplificada, pero realmente, hay tanto que cubrir que ¡probablemente necesitaríamos un artículo dedicado!

Antes de irnos, una cosa más.

El Anillo de Endomorfismos

Por último, quiero hablar de algo a lo que volveremos en algunos artículos.

Hay muchas posibles funciones de $E$ a sí mismo. Un ejemplo de esto fue el mapa de multiplicación por $m$ (que también es una isogenia). Llamamos a tales funciones endomorfismos. Ten en cuenta que las isogenias pertenecen a esta categoría.

Cambiar nuestro enfoque a los mapas mismos revela algo sorprendente: tienen una estructura de anillo. Sumar dos endomorfismos resulta en otro endomorfismo, y la multiplicación es simplemente la composición de estos mapas (también resultando en un endomorfismo).

El anillo generalmente se denota $\textrm{End}(E)$.

Un ejemplo de un endomorfismo que es bastante diferente de nuestro confiable mapa de multiplicación por $m$ es el endomorfismo de Frobenius, definido como:

$$\pi: E \rightarrow E \ / \ (x,y) \mapsto (x^p, y^p)$$

Esencialmente, simplemente toma las coordenadas de un punto y las eleva a la potencia de $p$ — el tamaño del campo finito. Hacer esto tiene una propiedad agradable: el mapa actúa trivialmente en los elementos del campo base $\mathbb{F}_p$, pero no en elementos de extensiones de campo. Por "actuar trivialmente", quiero decir que:

$$x, y \in \mathbb{F}_p \Rightarrow \pi(x,y) = (x,y)$$

Lo que significa que se comporta exactamente como la identidad (o para la multiplicación por $1$) para elementos en el campo base.

Esto es una consecuencia directa del pequeño teorema de Fermat.

Entonces, si restas $[1]P$ y $\pi(P)$, obtienes $\mathcal{O}$. Otra forma de decir esto es que el núcleo — generalización de raíces — de la función $[1] - \pi$ es la curva completa sobre el campo base. ¡Observa que $[1] - \pi$ es en sí mismo otro endomorfismo!

Además quizás de algunos otros puntos descarriados en la extensión de campo. Típicamente esto no solo no sucede, sino que veremos que no nos importan esos de todos modos.

Estas últimas cosas pueden sonar un poco rebuscadas o fuera de lugar. Pero créeme, son bastante útiles — y de hecho pondremos estos endomorfismos a buen uso pronto.

Resumen

¡Qué odisea! El estudio de funciones en curvas elípticas es bastante fascinante, y abre un mundo de posibilidades asombrosas.

Y mientras tanto, también introdujimos la idea de extensiones de campo, y permitimos que las curvas elípticas se definieran sobre estos campos más grandes.

Llegaré a eso pronto, lo prometo.

Cada uno de estos conceptos nos da una lente diferente a través de la cual podemos ver y entender las curvas elípticas. Y créeme — todavía hay mucho, mucho más por explorar.

En los próximos artículos, quiero abordar una herramienta fascinante en profundidad: los emparejamientos. Hablaremos nuevamente de grupos de torsión, extensiones de campo y todas las cosas buenas.

Antes de hacer eso, sin embargo, necesitamos aprender a entender el lenguaje de los divisores. Y ese será nuestro próximo destino. ¡Hasta la próxima!