Arkana | Cryptography 101: Arithmetic Circuits

This is part of a larger series of articles about cryptography. If this is the first article you come across, I strongly recommend starting from the beginning of the series.

Last time, we dove pretty deep into a particular example of a zero knowledge proof protocol. Optimizations and performance matters aside, it covered the desired use case: proving that a number is in a certain range. However, the protocol was tremendously specific, and crafting another protocol for another statement requires dedicated research, probably resulting in an entirely different sequence of steps.

We concluded by saying that a general framework for zero knowledge proofs could be an interesting endeavor to pursue.

And we’ll get there — just not right now!

The plan for today is to present some foundations upon which we’ll be building immediately after, in the next article.

Since we talked about bits in our previous encounter, let’s take a short detour and briefly review their uses. Shall we?

•••

Binary Circuits

Chances are if you’re reading this, you’re at least somewhat into computers, so let’s talk about that.

The fact that the bit is the basic unit for data representation in computer science is closely related to how computers work. Put simply, electric current flowing through a circuit may be considered a one ( $1$ ), while the state where no electric current flows through the same circuit may represent a zero ( $0$ ). And indeed, these currents are how bits are represented in the physical world.

But computers wouldn’t be nearly as cool as they are if we couldn’t perform some operations with said data.

The first thing we can do is to combine two bits (remember, they are just electrical signals), in various ways. For instance, we could create a box that only outputs $1$ when both signal inputs are also $1$ , and $0$ otherwise:

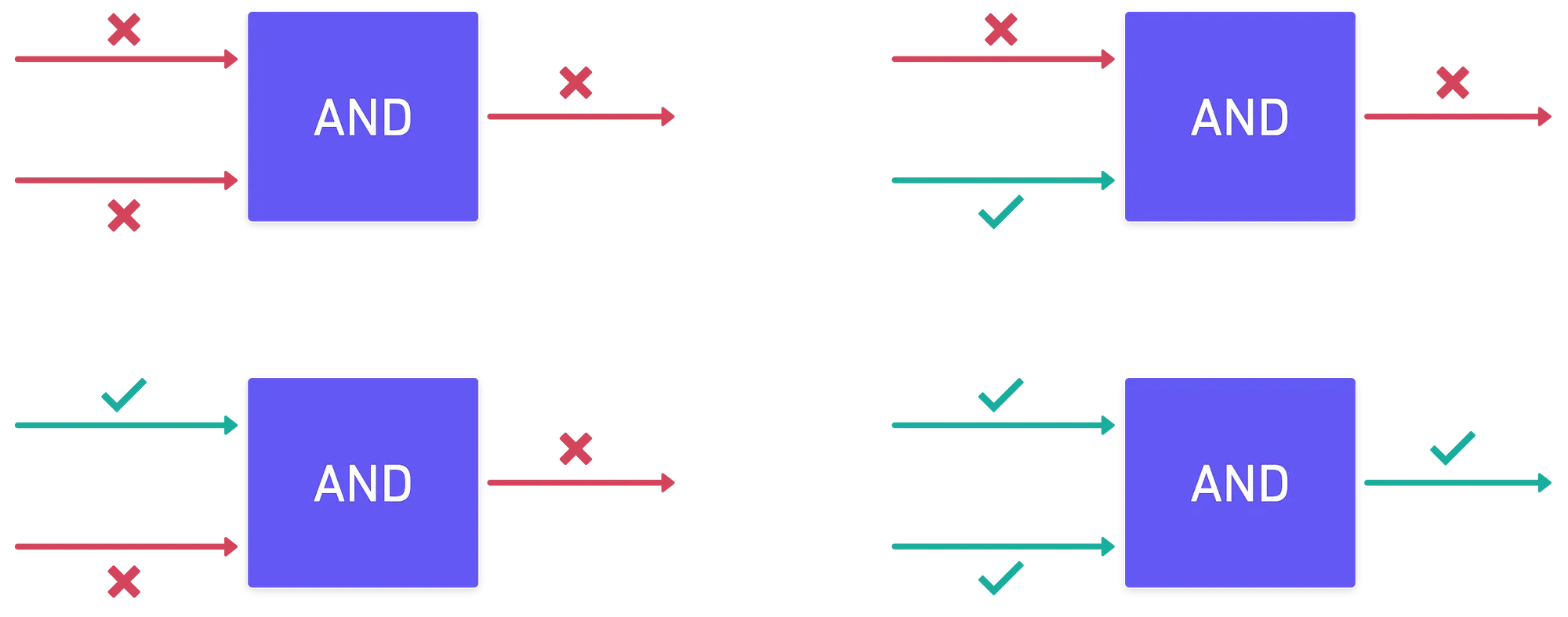
These types of boxes are called logic gates, and are what allow computers to do their magic. Other simple gates exist, such as $\textrm{NOT}$ , $\textrm{OR}$ , $\textrm{XOR}$ , $\textrm{NAND}$ , $\textrm{NOR}$ , and $\textrm{XNOR}$ — all of them being clever arrangements of electric circuits.

The two transistors in series in an AND gate — Roughly how the actual circuit for an AND gate looks like

Two signals is still too little — we can do better. So, we can process multiple inputs by laying down some gates, and obtaining a series of outputs in the process. The way the gates are laid out is called a circuit, which is essentially a model for computation.

For example, we can add two two-bit numbers $A = (a_0, a_1)$ and $B = (b_0, b_1)$ with this fairly simple circuit:

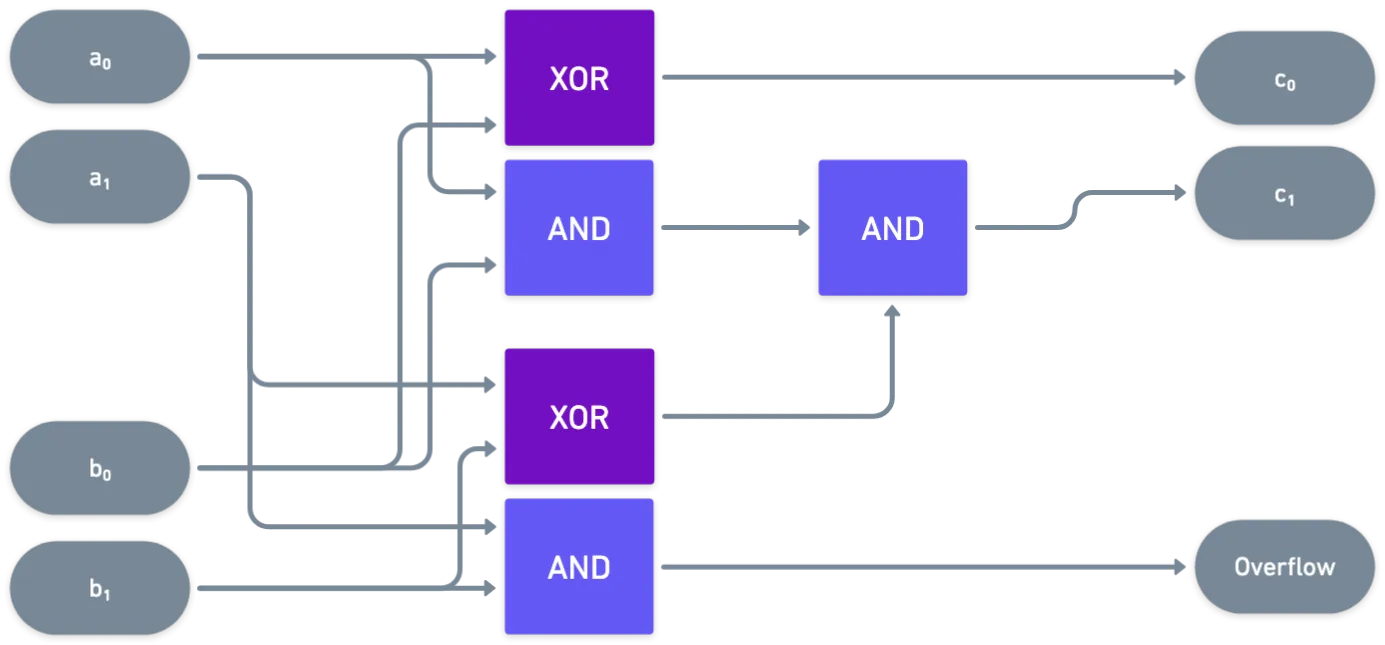
A circuit for a half-adder — The result may be 3-bits long — and this correspond to the third output, the overflow

All sorts of circuits for all sorts of purposes can be created by using multiple gates and handling multiple inputs.

Changing Perspectives

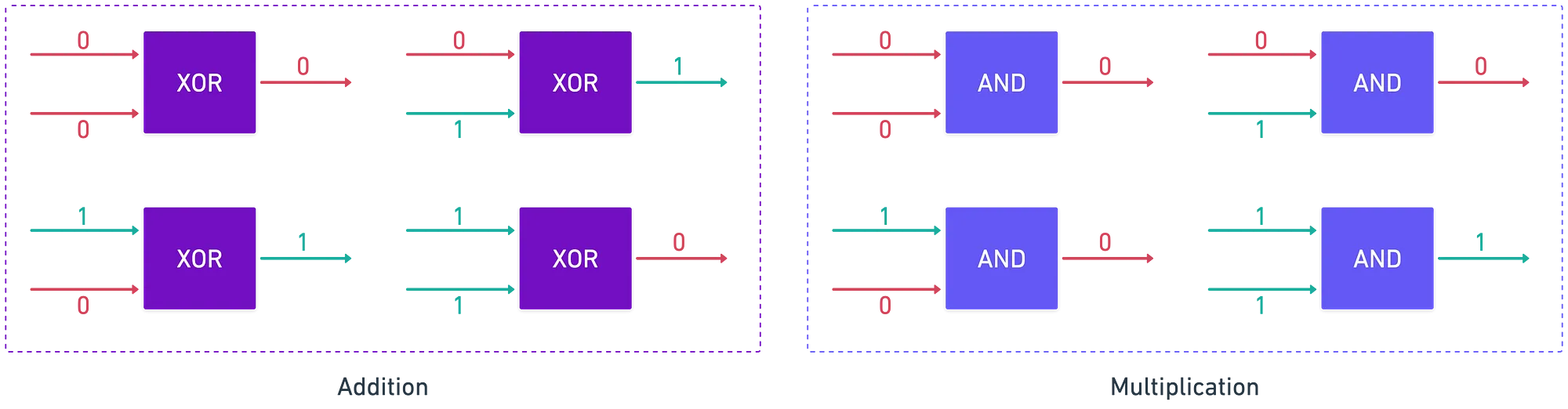
Let’s look at these binary circuits through another lens. A bit is simply a number that belongs to the set $\{0,1\}$ . And this set doubles up as a finite field: addition, multiplication, subtraction, and division (except by $0$ ) are all defined. We use the modulo operation so that we stay in range — for example, $1 + 1 \ \textrm{mod} \ 2 = 0$ .

In this sense, we could think of gates as mathematical operations over said finite field. An $\textrm{XOR}$ gate correctly represents addition modulo $2$ , while an $\textrm{AND}$ gate represents multiplication modulo $2$ :

Okay, cool… Now what?

Say we label the inputs as $x$ and $y$ . Let’s also throw in $1$ as an input, for good measure. What happens if we set up some gates?

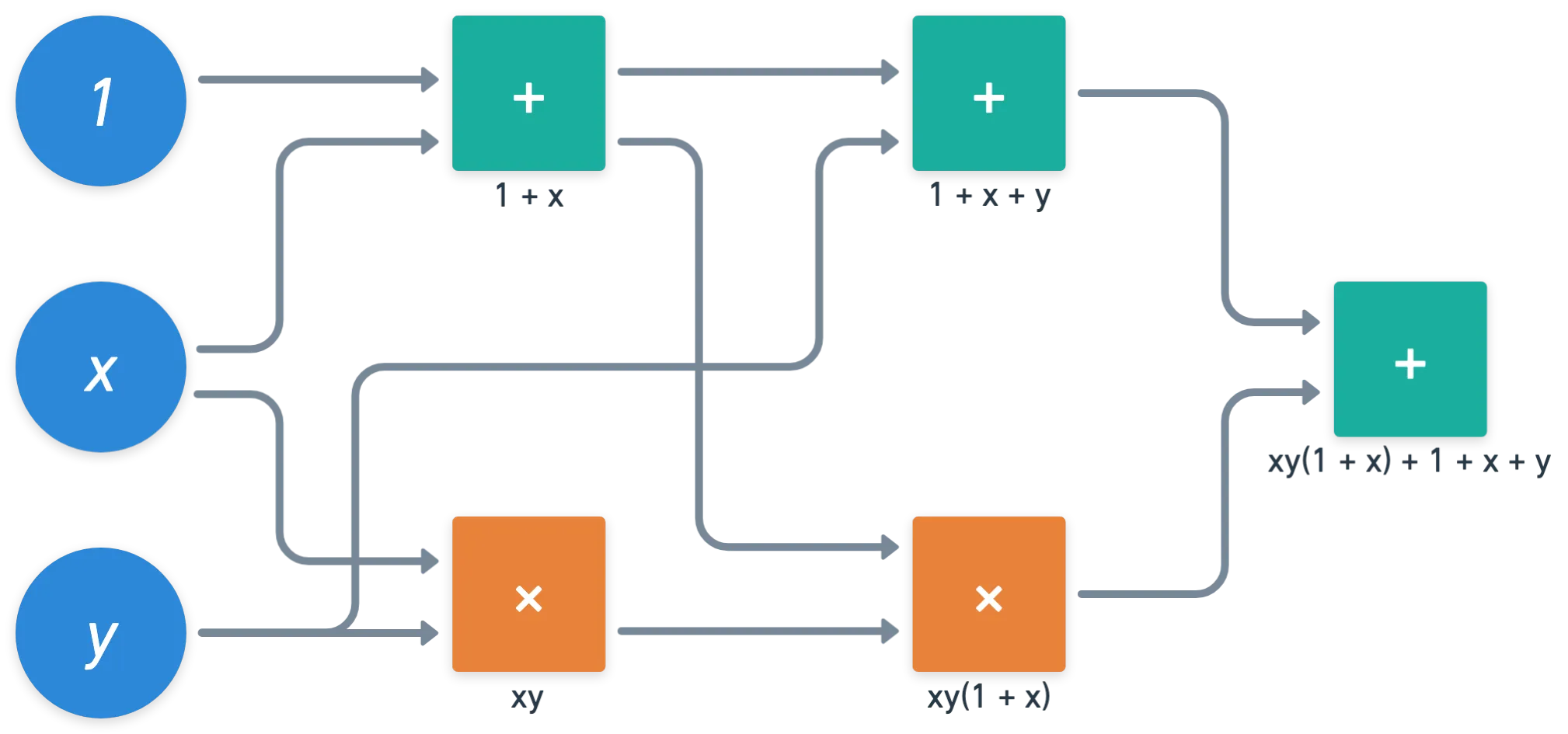
Some gates adding and multiplcating stuff

What’s that on the output? Is it... A polynomial? Nice!

Basically, we can represent a binary polynomial with just a bunch of addition and multiplication gates. In fact, it’s a prescription on how to compute the polynomial itself, step by step.

And we already know that polynomials have quite a few applications in cryptography. So here’s an idea: why limit ourselves to modulo $2$ ? What stops us from extending this recipe for computation into any arbitrary finite field?

Brain expansion meme — Giga brain activated

•••

Arithmetic Circuits

For a finite field with $q$ elements (for example, the integers modulo $q$ ), we can use the same type of circuiting to prescribe polynomial computation. The only difference with the previous circuit is that all operations are performed modulo $q$ instead of modulo $2$ , but that’s as far as differences go!

Another circuit forming a polynomial — If I’m not mistaken (feel free to corroborate!), this should result in the polynomial x⁴y² + 3x³y² + x³y + 2x²y² + 4x²y + 4xy

Formally, this is known as an arithmetic circuit. It’s just a graph, which maps inputs into nodes (called gates) that represent binary operations (here, binary means that each gate takes two inputs).

In their simplest version, the only gates that are used are addition and multiplication. These simple operations are really inexpensive to execute — making this a good calculation model in environments with constrained resources, such as Blockchains.

By the way, it’s important that the circuit is a directed acyclic graph (DAG), so that computation is only done forward, thus obtaining a unique result.

Why the Hassle?

At this point, you may be wondering “why define a graph and stuff, if you can compute the polynomial directly?”. As in, if you have the formula and the coefficients… Why not just do the calculations directly, and forget about the circuit?

Although this is fair, there are some considerations to make — about decomposability, parallelizability, generality, etc. We’ll see this in action further below.

For example, in homomorphic protocols, one might wish to perform operations that are known to preserve algebraic structure. And such operations are usually the “simple” addition and multiplication — decomposing a polynomial into its simple steps may then help in preserving algebraic properties, and thus, allowing homomorphic protocols to support complex computations.

•••

Application

Arithmetic circuits are yet another tool at our disposal. But as always, tools are worthless if they have no application.

Moving on, I want to focus on one aspect that is of particular interest for zero knowledge proofs. And to do this, let’s play some Sudoku.

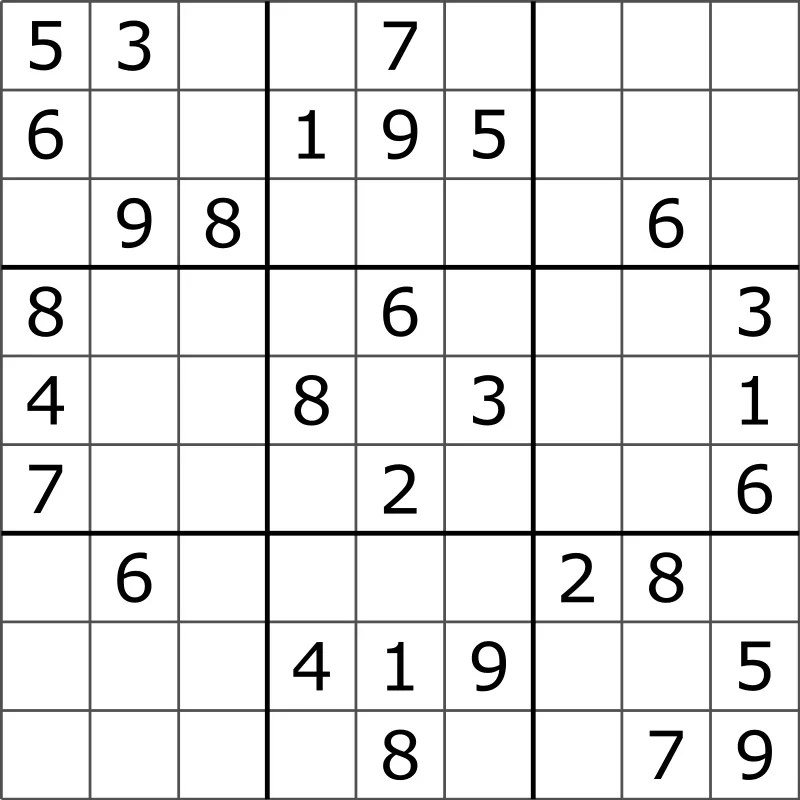
Sudoku game — Yeah, Sudoku. You heard that right!

Solving a good ol’ fashioned Sudoku is usually not that hard (although it can get really challenging sometimes!). What is for sure easier is to check if a given solution is valid — you know, as long as there are no repeated numbers in each row, column, and square box, we’re golden.

But you guys are thinking of the “standard” Sudoku, which is a $9 \times 9$ grid. The game could be expanded by using a larger grid, something like $16 \times 16$ , $25 \times 25$ , $100 \times 100$ , and so on. As the grid grows in size, the problem gets much, much harder. However, checking for a valid solution remains easy: you still check that there are no repeated numbers in each row, column, and square box.

This alludes to the fact that sometimes, verifying the solution of a problem is way easier than finding it — and this, we can use to our advantage.

If you’re keen about the subject, you may already have heard this cited as an example of the P vs NP problem. Really, it has not been proven that problems that are hard to solve and easy to verify really exist — this is, it has not been mathematically proven that it’s harder to solve a giant sudoku, than to verify it.

And this is so pivotal for computer science, that there’s a one-million dollar bounty for anyone that proves whether if P = NP or not.

Yeah, it’s that important.

Checking the Solution

Verification, as previously mentioned, happens by checking that numbers are not repeated. How about we try writing this in the form of equations?

Robert Downey Jr. rolling eyes meme — Hang in there, my friend

If numbers should not be repeated, this means that each row, column, and square should sum up to the same number, $S$ :

S = \sum_{i=1}^n i

And I think nobody will complain if I represent the values of a Sudoku as a matrix — I mean, it’s even a square! Served up on a plate for us.

\begin{bmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n^2}\\ a_{2,1} & \ddots & & \vdots \\ \vdots & & \ddots & \vdots \\ a_{n^2,1} & \cdots & \cdots & a_{n^2,n^2} \\ \end{bmatrix}

Some of these values are of course prescribed, since the puzzle needs an initial state so that it only has one solution.

Focus for a second on column $1$ . If we sum up all the elements, a valid solution should give the expected value $S$ :

S = \sum_{i=1}^n a_{i,1}

Of course, we have to write the same type of check for each row, column, and square — yielding a grand total of $3n$ equations. Even if a single one of those checks fails, then we immediately know the solution is invalid.

And these equations can be represented as a very simple arithmetic circuit! Just, perhaps, with quite a lot of addition gates.

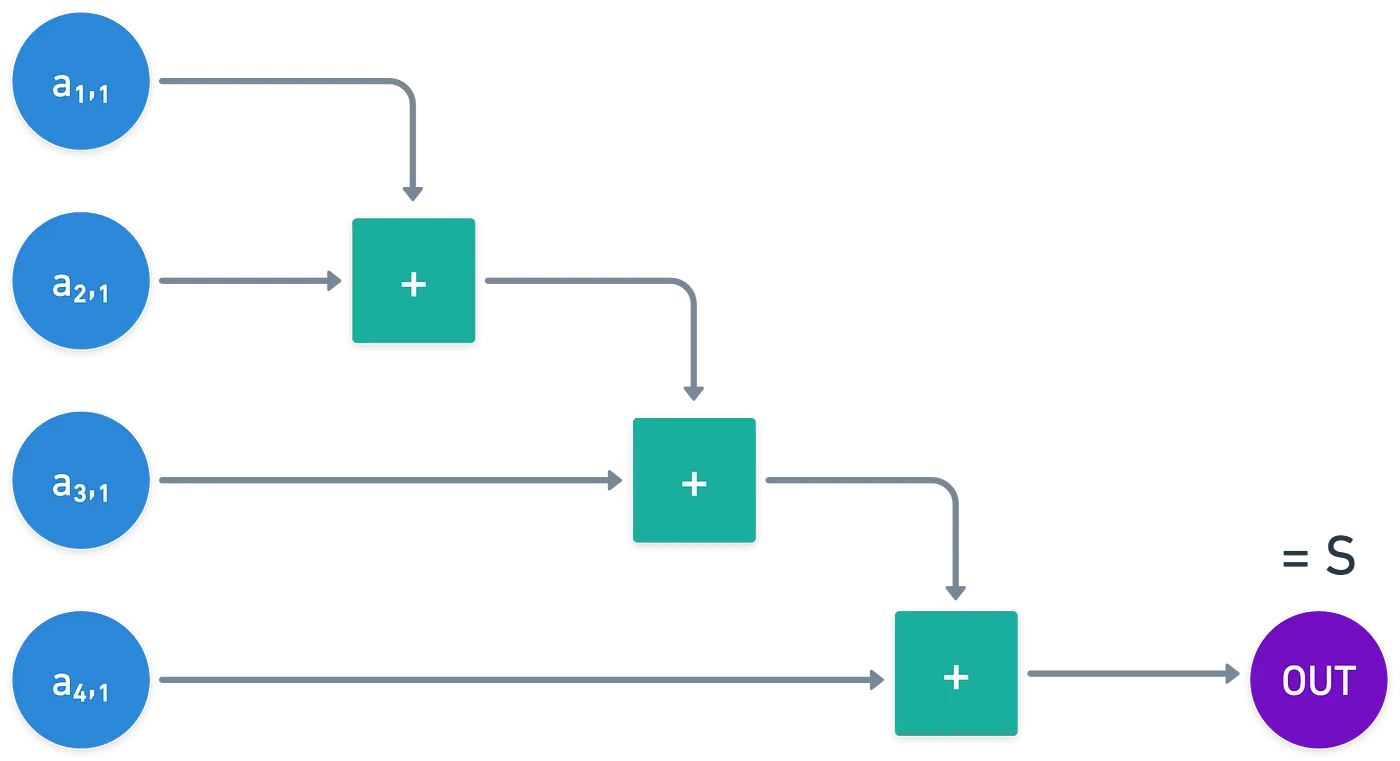
A circuit for a 4x4 sudoku — The circuit for a column on a 4x4 sudoku. The output should be S = 10

We now have a general computation model for verification of a solution to a problem. In other words, knowledge of a solution. So, when working with proofs of knowledge, we could build a circuit that represents the verification of a solution to a problem of choice.

Said problem could help us prove a myriad of statements: that a number is on a given range, that we know some discrete logarithm, that we know the hash of a value — really, a lot of statements. And this is what gives arithmetic circuits their flexibility!

Chris Pratt looking extremely excited — Okay maybe you don’t look THIS excited

•••

A Note on Zero Knowledge

Fantastic! We now know that given some statement, we can craft an arithmetic circuit to represent its verification. Except that verification requires the inputs to the circuit!

In zero knowledge proofs, we would like to avoid disclosing said inputs (or at least, the ones that should be private). So what do we do? Did we introduce arithmetic circuits for nothing?

Human body with chest in red, signaling pain, as in commercials — *Pain intensifies*

Worry not, dear friend — it was not for naught.

Because arithmetic circuits can be decomposed into simple elements (their gates), we can do some magic that will allow a verifier to check for a valid computation without knowledge of the chosen inputs. We’ll get to that soon!

•••

Summary

This post introduced the notion of arithmetic circuits, and their role as a general computation model. In this sense, we discussed how they can be used to verify solutions to a problem — being that the problem is correctly represented by the arithmetic circuit.

Arithmetic circuits are general models for computation that are easily decomposed into their building blocks: gates.

And we mentioned how these arithmetic circuits can be easily decomposed, and how this will help in the “zero” aspect of zero knowledge proofs. This, however, will involve some new mathematical feats.

Explaining those feats, which will ultimately lead to us building a zero knowledge proof protocol, will be the central topic for next article. Until then!