Criptografia 101: Assinaturas de Limite

Este é parte de uma série de artigos sobre criptografia. Se este é o primeiro artigo que você encontra, eu recomendo começar do início da série.

No artigo anterior, aprendemos sobre polinômios e vimos algumas de suas aplicações.

No entanto, esta nova peça de criptografia parece desconectada de tudo que aprendemos até agora. Ainda assim, há maneiras interessantes de combiná-la com conceitos anteriores, como assinaturas digitais.

Este artigo será dedicado exclusivamente a explicar um exemplo disso, onde combinaremos as técnicas de assinatura usuais com polinômios, para criar um esquema híbrido interessante. Trabalharemos no contexto de curvas elípticas, e usaremos $G$ e $H$ para denotar geradores de grupo para um grupo $\mathbb{G}$.

Basearei minha explicação vagamente neste paper, com alguns ajustes na esperança de tornar as coisas mais fáceis de navegar.

Ainda assim, um aviso amigável: assinaturas de limite não são simples de explicar. Há muitas nuances que precisaremos esclarecer. Então, vamos primeiro ver um breve resumo do que elas são e o que fazem, antes de realmente mergulhar na matemática por trás delas.

Assinantes Suficientes

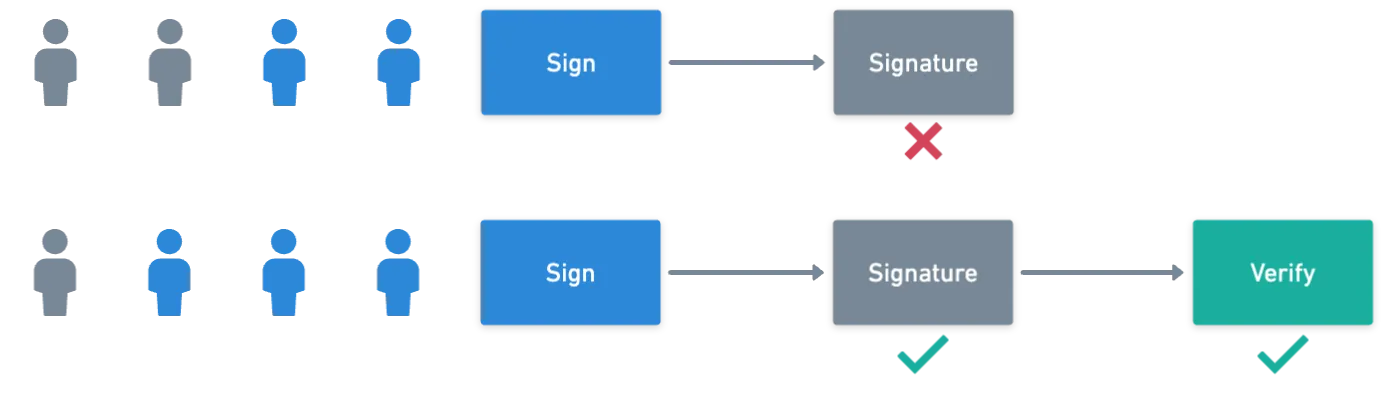
Assinaturas de limite são um tipo de multissinatura — significando que múltiplos participantes são necessários para assinar uma mensagem. Mas desta vez, não é necessário que todos os participantes façam isso.

Imagine um grupo de dez pessoas que têm privilégios de administrador para uma aplicação. Para realizar alguma ação sensível, exigimos pelo menos três aprovações.

Dessa forma, não precisamos incomodar todos os administradores ao mesmo tempo; apenas um subconjunto de assinantes disponíveis será suficiente.

Isso parece uma melhoria ao esquema de multissinatura que exploramos anteriormente, onde todos os assinantes eram obrigatórios a participar. Mas na realidade, alcançar este resultado envolve flexionar alguns músculos criptográficos mais.

Click to zoom

Podemos dividir assinaturas de limite em três passos principais ou algoritmos (como a maioria dos esquemas de assinatura):

• Geração de chaves (KeyGen), que é um algoritmo que produz um par de chaves privada compartilhada e pública,
• Assinatura, onde uma mensagem é processada junto com a chave privada e um nonce para obter um par $(r, s)$,
• E verificação, o passo onde a assinatura é validada contra a mensagem e a chave pública.

Quando trabalhamos com esquemas de assinatura de limite, os passos de geração de chaves e assinatura, que eram bastante diretos em exemplos passados, serão substituídos por processos mais complexos envolvendo comunicações entre os assinantes. Felizmente, a verificação permanece a mesma — então nosso foco ficará nos dois primeiros passos.

Note que a ideia de exigir um limite de assinantes é muito reminiscente da quantidade mínima de pontos para reconstruir um polinômio via interpolação. E de fato, isso está no núcleo de como assinaturas de limite funcionam.

Além disso, para manter as coisas claras, devemos dizer que os assinantes ou participantes são ordenados. Cada um terá um identificador ou índice, variando de $1$ a $n$, o número total de participantes.

Nossos objetivos estão definidos, e a introdução acabou. Vamos ao que interessa?

Preliminares

Em protocolos de limite, compartilhar informação é fundamental. Em última análise, a capacidade de um conjunto de assinantes compartilhar informação é o que permitirá que eles produzam assinaturas.

Já vimos que compartilhar um segredo pode ser alcançado com Compartilhamento de Segredo de Shamir (SSS). A ideia era avaliar um polinômio em muitos valores diferentes, e compartilhar os resultados como pontos. E com esses pontos, poderíamos interpolar de volta o polinômio original.

Mas há um problema. Como qualquer receptor pode verificar se os valores que eles recebem estão calculados corretamente? Ou, em outras palavras, há um jeito de provar que os pontos estão efetivamente relacionados ao polinômio original?

E você pode estar se perguntando por que os valores estariam incorretos? Por que alguém enviaria um valor errado? Há pelo menos duas razões a considerar: erros na comunicação e atividade maliciosa. É possível que um atacante possa estar tentando quebrar nosso modelo de assinatura — não podemos necessariamente esperar que todos se comportem corretamente, e devemos tomar ação para mitigar este possível cenário.

Para abordar esta preocupação, precisaremos de uma nova ferramenta.

Compartilhamento de Segredo Aleatório Verificável

O que fazemos é pedir ao compartilhador para fazer um compromisso. Isso vinculará o compartilhador à sua informação secreta (seu polinômio), para que depois eles simplesmente não possam produzir valores inválidos.

Esta ideia é o que está por trás do Compartilhamento de Segredo Aleatório Verificável (VRSS), uma espécie de substituto direto para SSS. O que queremos fazer é nos comprometer com os coeficientes do nosso polinômio — e para isso, precisaremos não de um, mas dois deles:

$$f_i(x) = a_{i,0} + a_{i,1}x + a_{i,2}x^2 + ... + a_{i,t}x^t$$ $$f_i'(x) = b_{i,0} + b_{i,1}x + b_{i,2}x^2 + ... + b_{i,t}x^t$$

Por que, você pergunta? Porque compromissos precisam ser ocultadores. Não queremos revelar os coeficientes, então seus compromissos devem ser cegados. Os coeficientes do segundo polinômio são de fato esses fatores de cegamento!

Então, usando nossos geradores de grupo, cada participante $i$ calcula e transmite os valores de compromisso $C_i$, um para cada um dos coeficientes nos polinômios:

$$C_{i,m} = [a_{i,m}]G + [b_{i,m}]H$$

Legal! Agora tudo que resta é compartilhar. E para isso, todos precisarão avaliar seu polinômio. Como cada participante tem um índice $j$, podemos fazer a escolha de avaliar a parte para um jogador alvo no seu índice, então $f_i(j)$.

O que isso significa é que indivíduos receberão $f_i(j)$ e $f_i'(j)$ de algum outro participante $i$.

E ao receber estes valores, o participante $j$ pode validá-los da seguinte forma:

$$[f_i(j)]G + [f_i'(j)]H = \sum_{m=1}^{t-1} [(j)^m]C_{i,m}$$

Isso é basicamente tudo! Agora temos um mecanismo para compartilhar informação secreta, de uma forma que é verificável. Com esta ferramenta, podemos começar a construir nosso esquema de assinatura.

Geração de Chaves

Como há múltiplas partes envolvidas em assinaturas de limite, cada participante terá um inteiro $d_i$ como sua parte (ou pedaço) de uma chave privada.

No entanto, este não é um inteiro escolhido aleatoriamente, como de costume. Em vez disso, os participantes se envolvem em um processo onde interagem uns com os outros, produzindo finalmente sua parte da chave privada. Esses tipos de protocolos são chamados algoritmos de Geração de Chave Distribuída (DKG).

E podemos usar VRSS para construir nosso algoritmo. Que conveniente!

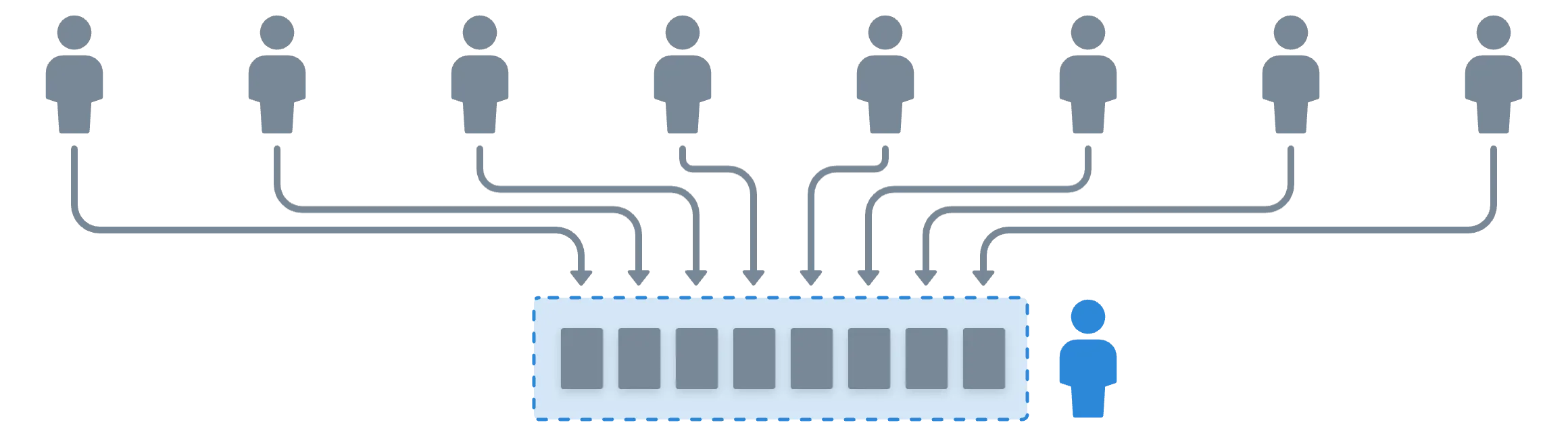
A ideia é que cada participante receberá uma parte de cada um de seus pares, e eles usarão estes valores verificados para calcular sua parte da chave privada:

$$d_i = \sum_{j=1}^m f_j(i)$$

É possível que alguns valores não passem na verificação; algumas partes podem ser desqualificadas neste caso. É por isso que VRSS é importante.

Ainda assim, vamos seguir o caminho feliz para manter as coisas relativamente simples.

A saída do DKG é um pedaço de uma chave privada compartilhada, $d$. Nenhuma das partes envolvidas neste protocolo conhece este valor — apenas seus pedaços.

Click to zoom

Finalmente, precisamos de uma chave pública. E para isso, cada participante transmite seu coeficiente secreto independente ou zero, $a_{i,0}$. Este segredo não pode ser divulgado como tal, e portanto, é transmitido como uma parte da chave pública:

$$Q_i = [a_{i,0}]G$$

Acho bastante estranho ver a parte da chave pública sendo calculada assim. Aposto que você esperava ver $d_i$ ali!

Há uma boa razão para não ser usado, no entanto. Voltaremos a esta afirmação mais tarde, porque precisaremos definir algumas coisas para entender o que realmente está acontecendo.

Uma vez que todas as partes são públicas, então cada participante pode calcular a chave pública global independentemente:

$$Q = \sum_{i=1}^m Q_i$$

Para finalizar, aqui está um breve resumo para este passo:

A geração de chaves envolve partes se comunicando umas com as outras, gerando pedaços de uma chave privada compartilhada. Nenhum jogador conhece a chave privada compartilhada. Uma chave pública que está associada com o segredo compartilhado também é calculada.

Com todas as chaves no lugar, tudo que resta é assinar.

Assinando uma Mensagem

A primeira coisa que precisaremos é uma mensagem para assinar. Isso não é trivial, no entanto, porque todos precisam concordar com uma mensagem. Não cobriremos como isso acontece — vamos apenas assumir que todos conhecem a mensagem $M$ sendo assinada.

No ECDSA, um assinante tipicamente escolheria um nonce aleatório $k$, e calcularia um desafio $R = [k]G$ correspondentemente, produzindo uma assinatura assim:

$$s = k^{-1}(H(M) + d.r) \ \textrm{mod} \ n$$

Mas como já vimos, esta não é como a criptografia de limite tende a operar. Em vez disso, um grupo de $t$ assinantes se comunicará uns com os outros para produzir uma assinatura. E a primeira coisa que eles precisarão é de um nonce.

Felizmente, já temos uma ferramenta para gerar um valor distribuído: DKG! Vamos apenas dizer que assinantes executam uma rodada de DKG, obtendo uma parte $k_i$, e um desafio associado:

$$R_i = \sum_{i=0}^m R_i$$

Para a computação da assinatura, todos usarão a coordenada x de $R$, que denotaremos $r$.

Construindo a Assinatura

Como você provavelmente pode adivinhar a esta altura, a geração da assinatura também é feita em partes. E novamente, a ideia é que apenas quando um certo número de partes está disponível, seremos capazes de produzir uma assinatura válida através da agregação dessas partes calculadas independentemente.

Nosso requisito é o seguinte: as partes da assinatura $s_i$ devem interpolar para a assinatura final $s$ — que deve passar na verificação quando usando a chave pública $Q$. A coisa mais natural a fazer aqui é adaptar a expressão para $s$ para que use partes de seus componentes em vez disso:

$$s_i = k_i^{-1}H(M) + k_i^{-1}d_i.r \ \textrm{mod} \ n$$

Mas isso faz sentido? Aqui, temos uma adição, multiplicações, e até inversos modulares. Não parece óbvio assumir que isso funcionará assim mesmo.

Parece justo examinarmos esta expressão e verificar que funciona adequadamente. E realmente, não é tão complicado quanto você imaginaria. Vamos devagar, um passo de cada vez.

Interpolando Adições

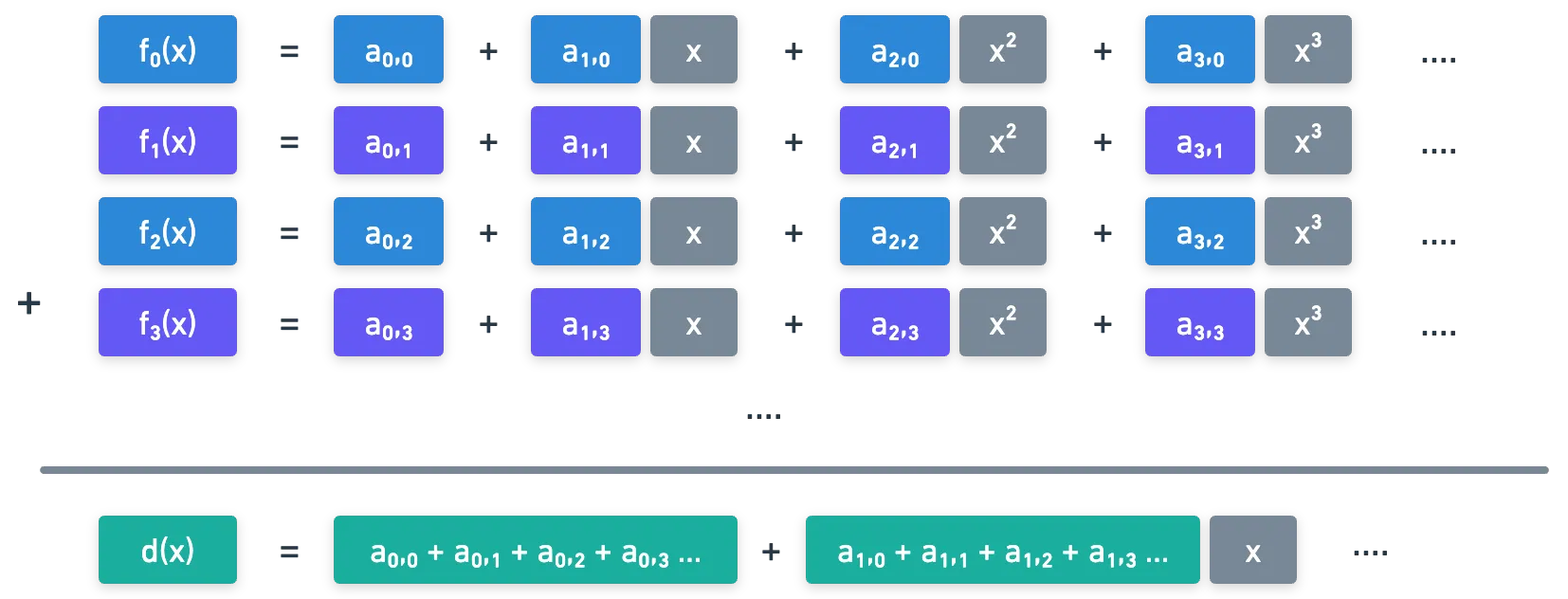
Para nos começar, digamos que temos dois polinômios $a(x)$ e $b(x)$. Se os avaliarmos em diferentes valores $i$, obtemos conjuntos de pontos da forma $(i, a(i))$ e $(i,b(i))$. Por conveniência, vamos apenas denotá-los $a_i$ e $b_i$:

$$a_i = (i, a(i)) b_i = (i, b(i))$$

Sabemos que qualquer subconjunto de t pontos desses pontos nos permite interpolar de volta os polinômios originais. E se definirmos o termo independente de $a(x)$ como $a$, poderíamos escrever que:

$$a \leftarrow \textrm{interpolate}(a_1, ..., a_t)$$

Como lembrete, no contexto de compartilhamento de segredo, geralmente estamos interessados no termo independente. É por isso que quando dizemos que interpolamos alguns valores, podemos nos referir à saída como apenas este coeficiente independente ou zero, e não ao polinômio inteiro. Mas realmente, a saída completa é o polinômio inteiro!

Similarmente, vamos assumir que temos pontos onde $b(x)$ tem termo independente $b$, e então:

$$b \leftarrow \textrm{interpolate}(b_1, ..., b_t)$$

Agora, o que acontece se somarmos os polinômios $a(x)$ e $b(x)$?

Click to zoom

Podemos somar termo por termo, e terminamos com um polinômio com o mesmo grau dos originais ($t - 1$), mas onde o termo independente é $g = a + b$. Além disso, como $g(x) = a(x) + b(x)$, então todos os pontos que interpolam para $g$, que são $(i, g(i))$, podem ser calculados como $a_i + b_i$. E então:

$$g \leftarrow \textrm{interpolate}(a_1 + b_1, ..., a_t + b_t)$$

E isso é incrível! Isso significa que podemos essencialmente somar partes de um polinômio, e quando interpolando, obteremos como resultado a soma dos segredos compartilhados. Legal!

Agora podemos analisar o cálculo da chave pública. Lembre-se de que a parte $d_i$ é calculada como a soma dos valores $f_j(i)$.

Por causa disso, $d_i$ é essencialmente uma parte de uma soma de polinômios, cujo termo independente será a soma de todos os termos $a_{i,0}$. O que significa que o resultado de interpolar todos os $d_i$ produzirá essa soma!

Click to zoom

E essa é a razão pela qual a chave pública é calculada do jeito que é. Tudo se encaixa!

$$\sum_{i=0}^m a_{i,0} \leftarrow \textrm{interpolate}(d_1, ..., d_m)$$ $$Q = \left [ \sum_{i=0}^m a_{i,0} \right ]G = \sum_{i=0}^m [a_{i,0}]G$$

Interpolando Produtos

Produtos são ligeiramente mais complicados. Quando multiplicamos $a(x)$ e $b(x)$, o polinômio resultante $h(x)$ terá o dobro do grau. E por causa disso, precisamos de duas vezes tantos pontos para interpolação:

$$h \leftarrow \textrm{interpolate}(a_1.b_1, ..., a_{2t-1}.b_{2t-1})$$

E isso não é realmente ótimo, porque agora precisamos de mais valores para interpolar, o que significa mais comunicações entre pares.

Independentemente deste inconveniente, a boa notícia é que isso se comporta do jeito que esperamos: quando multiplicamos $h(x) = a(x)b(x)$, os termos independentes também são multiplicados, e nossos valores $a_ib_i$ também interpolarão para $h = ab$!

Também vale mencionar: quando multiplicamos partes por uma constante, a interpolação resultante também será multiplicada por ela:

Click to zoom

Então se tomarmos nossas partes como $(i, k.a_i)$, então a interpolação produzirá $k.a$. Bem direto, né?

Tudo bem, só temos mais um caso para analisar. A dor e o sofrimento acabarão prontamente, eu prometo.

Interpolando Inversos

Realmente, tudo que está faltando é lidar com aquele maldito inverso modular. O que queremos é produzir valores ${k_{i}}^{-1}$ que, quando interpolados, produzam $k^{-1}$. Isso vai levar alguns passos. É.

• Primeiro, todos executarão uma rodada de VRSS para produzir partes $\alpha_i$. Claro, essas partes interpolam assim:

$$\alpha \leftarrow \textrm{interpolate}(\alpha_1, ..., \alpha_m)$$

• Em seguida, cada participante calculará e transmitirá:

$$\mu_i = \alpha_i.k_i$$

• Como $\mu_i$ é o resultado de uma multiplicação, ao receber $2t-1$ partes, qualquer um poderia interpolar este valor:

$$\mu \leftarrow \textrm{interpolate}(\mu_1, ..., \mu_{2t-1})$$

• Finalmente, cada participante calcula ${k_{i}}^{-1}$ desta forma:

$${k_{i}}^{-1} = \mu^{-1}.\alpha_i$$

Como essa magia funciona, você pergunta? Bem, considere isso: $μ^{-1}$ age como um termo constante quando interpolando os valores ${k_{i}}^{-1}$. E por causa disso, terminamos com:

$$\mu^{-1}.\alpha \leftarrow \textrm{interpolate}({k_1}^{-1}, ..., {k_{2t-1}}^{-1})$$ $$\mu^{-1}.\alpha = k^{-1}.\alpha^{-1}.\alpha = k^{-1}$$

E como mágica, construímos valores que interpolam para o inverso de $k$!

Isso é tudo que vamos precisar! Vamos verificar de volta nosso cálculo de assinatura com nossas conclusões recém-encontradas.

De Volta à Assinatura

Se pudéssemos reconstruir cada segredo compartilhado, então o cálculo da assinatura aconteceria como no ECDSA padrão:

$$s = k^{-1}H(M) + k^{-1}dr \ \textrm{mod} \ n$$

Mas na prática, não queremos que isso aconteça — e só temos partes. E então nos perguntamos se isso:

$$s_i = {k_i}^{-1}H(M) + {k_i}^{-1}d_ir \ \textrm{mod} \ n$$

também interpolou para $s$. E a resposta é um retumbante sim, porque estamos apenas lidando com adições, produtos e inversos — e já sabemos como estes se comportam.

Talvez o único problema aqui seja que como estamos lidando com um produto de partes (o termo ${k_i}^{-1}d_ir$), precisaremos de como $3t-2$ partes para interpolar. Mas deixando isso de lado, temos certeza de que interpolar os valores $s_i$ produzirá o valor esperado de $s$!

Protocolos diferentes podem fazer uso de várias técnicas para tentar mitigar a necessidade de pontos extras para interpolação — e idealmente, gostaríamos de manter esse número o mais próximo de $t$ possível. Além disso, quanto menos passos de comunicação forem necessários, melhor.

Para finalizar, quando cada participante calcula sua parte $s_i$, eles simplesmente a transmitem. E quando partes suficientes estão disponíveis, qualquer um pode interpolar, produzir e gerar $s$.

E aí está! Simples, né?

Estou brincando, claro — isso é qualquer coisa menos simples. Mas a ideia geral é o que realmente é a conclusão chave:

Durante a assinatura, partes novamente se comunicam umas com as outras, gerando pedaços de uma assinatura compartilhada. Quando pedaços suficientes estão disponíveis, a assinatura final pode ser construída; com menos pedaços do que necessário, simplesmente não é possível.

A verificação acontece como de costume, porque a saída da assinatura é simplesmente o par $(r, s)$.

Resumo

Acho que este é o artigo mais tecnicamente carregado que escrevi até agora. Tentei ao máximo mantê-lo simples, mas há algumas coisas que simplesmente não podemos evitar explicar. No mínimo, espero que isso esclareça alguns aspectos que, pela minha experiência, geralmente não são explicados em detalhes.

🔥 Importante: Na verdade há uma vulnerabilidade bem grande no processo que descrevi, onde partes da chave privada vazam quando compartilhando $s_i$.

Isso é abordado no paper que usei como guia, e a solução é na verdade bem simples. Então por favor, não vá usar este artigo para construir suas assinaturas de limite — e talvez consulte o paper real em vez disso!

Projetar esse tipo de protocolos de Computação Multi-Partes, onde há comunicação entre partes, requer considerar que atividade maliciosa pode existir. Então em geral, esses protocolos são cheios de rodadas de desqualificação, provas de correção, talvez até alguma encriptação, e outras coisas divertidas. Realmente, eles são uma consolidação de muitas técnicas diferentes, e tendem a ser complexos.

Computação Multi-Partes é, em geral, bem complexa.

Este é realmente o esquema mais simples que consegui encontrar em termos de que ferramentas são necessárias, e é apresentado principalmente na esperança de ilustrar os componentes principais dessas técnicas. E isso significa que quanto mais ferramentas pudermos acumular, mais fácil será criar esquemas mais complexos.

Dito isso, nossa jornada continuará apresentando outra ferramenta extremamente poderosa, que desbloqueará novos tipos de funcionalidade: emparelhamentos. Vejo vocês no próximo!