Criptografia 101: Polinômios

Este é parte de uma série de artigos sobre criptografia. Se este é o primeiro artigo que você encontra, eu recomendo começar do início da série.

Até agora na série, investimos muito em aprofundar nossa compreensão da Criptografia de Curvas Elípticas (ECC). Fizemos um breve desvio para introduzir as funções hash, mas isso é o máximo que nos desviamos do nosso tema central.

Embora a ECC seja muito rica e poderosa, há muito mais na criptografia do que apenas isso. E nesta seção, quero apresentar a você o fantástico mundo dos polinômios.

Podemos fazer algumas coisas com eles que não podem ser alcançadas com curvas elípticas. Então vamos começar apresentando-os, e depois veremos suas aplicações. Vamos lá!

Polinômios

Você provavelmente já viu esses caras em algum momento durante o ensino médio. Em essência, são muito simples: consistem em uma expressão que envolve variáveis, que só podem ser somadas, subtraídas e multiplicadas. A multiplicação também implica que podemos ter potências de variáveis. E cada termo na soma pode ser multiplicado por um número, chamado coeficiente. Algo como isso:

$$P(x,y) = x^4 + 3yx^3 - y^2x^2 + 6y - 1$$

Podemos notar que um polinômio pode ter múltiplas variáveis diferentes. Não há limitação nesse sentido, mas na maioria dos casos, usaremos apenas uma variável e a denotaremos como $x$.

Como curiosidade, somar dois polinômios resulta em outro polinômio, e multiplicar dois polinômios também resulta em outro polinômio; por causa disso, o conjunto de todos os polinômios forma um objeto matemático chamado anel.

Polinômios têm aplicações em várias áreas da matemática. Também são úteis em criptografia, mas sob uma condição: devemos usar inteiros em todos os lugares. Isso significa que às variáveis só serão dados valores inteiros, e não podemos ter polinômios com coeficientes como $0.5$. Isso garante que o polinômio exclusivamente gere inteiros como resultado.

Além disso, em criptografia, normalmente operamos sob a operação módulo. Então uma expressão completa para o polinômio, se você quiser, se pareceria com algo assim:

$$P(x) = x^4 + 3x^3 - x^2 + 6 \ \textrm{mod} \ q$$

Finalmente, o grau de um polinômio é definido pela potência mais alta à qual a variável é elevada. Por exemplo, o polinômio que acabamos de ver tem grau $4$.

Este é tipicamente o ponto onde alguém começaria a se perguntar "por que preciso saber sobre isso?"

Sim, eu sei. Prometo que as aplicações serão muito interessantes. Por favor, tenha paciência, porque ainda precisamos introduzir um tipo particular de polinômio que será extremamente útil para nós: os Polinômios de Lagrange.

Interpolação

Você já notou como só há uma única linha possível que passa por dois pontos?

Click to zoom

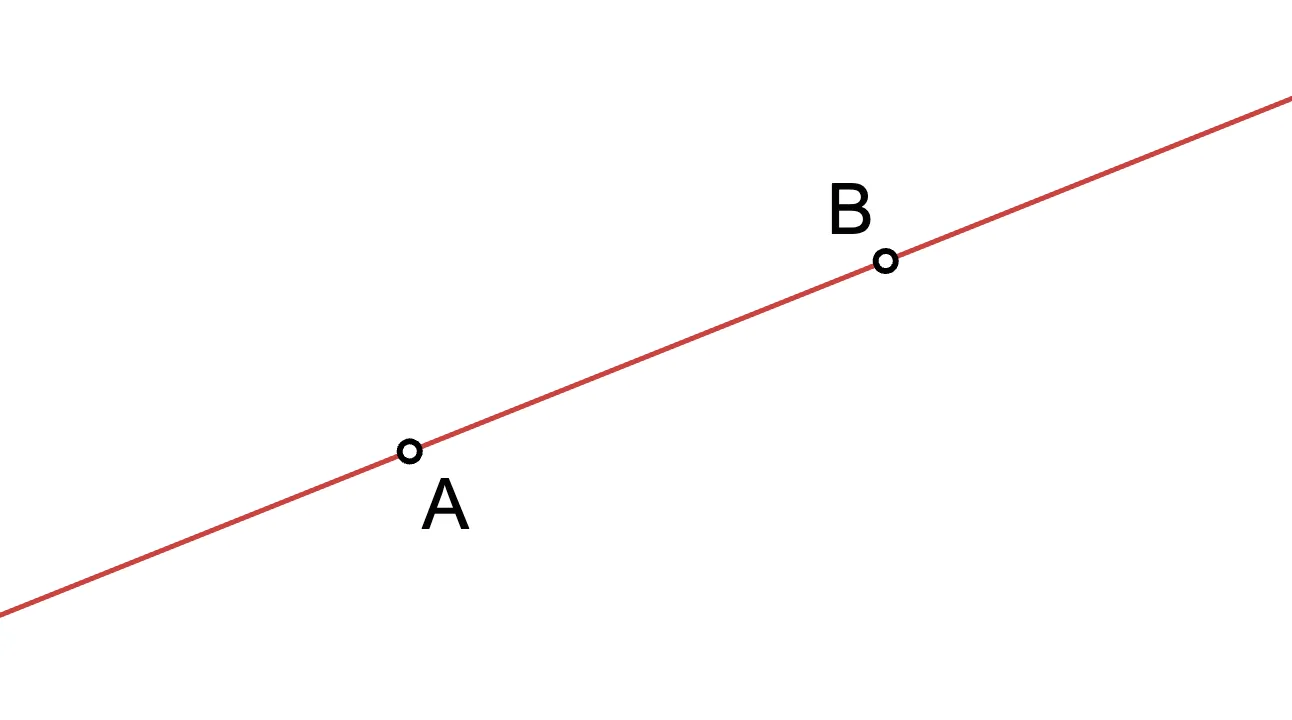
Por mais que você tente, não há outra linha que passe por $A$ e $B$. E uma linha é realmente uma função polinomial, $P(x) = m.x + n$. E isso não é uma coincidência.

Vamos tentar agora com três pontos. Eles podem estar alinhados, caso em que você pode desenhar uma linha que passe por eles, ou não alinhados. No último caso, você pode desenhar uma, e só uma parábola (um polinômio de grau 2) que passe por eles.

Click to zoom

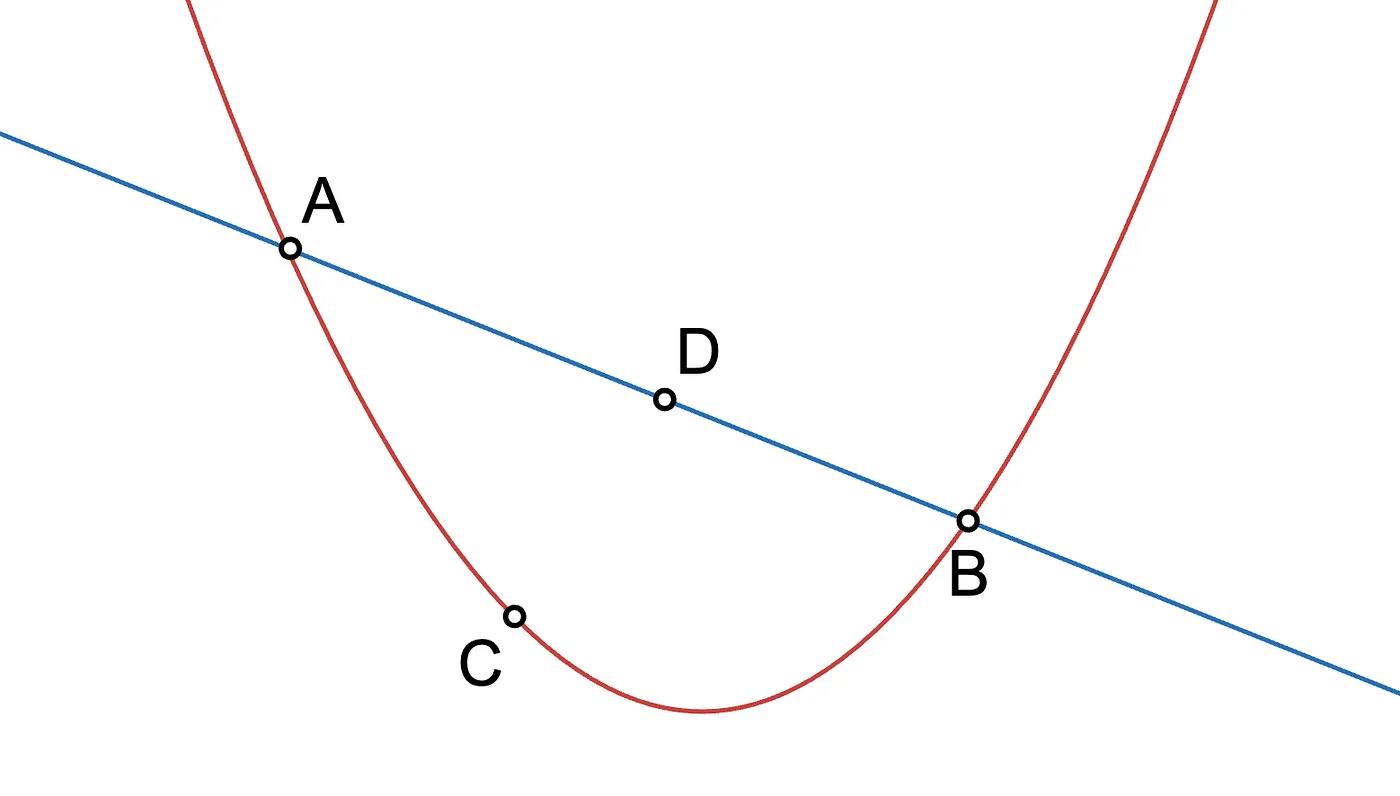
Só para esclarecer, já que usamos inteiros e a operação módulo, as curvas são apenas uma forma de visualizar o que está acontecendo, mas realmente usamos pontos discretos.

Em geral, para um conjunto dado de $m$ pontos, há um polinômio único de grau no máximo $m - 1$, que passa por todos os $m$ pontos. Este polinômio é muito especial, tanto que recebe seu próprio nome: um Polinômio de Lagrange. Dizemos que interpola os $m$ pontos.

O que o torna tão especial? Para entender, vamos fazer um pequeno exercício:

Pegue três pontos quaisquer com valores inteiros $(x_1, y_1)$, $(x_2, y_2)$ e $(x_3, y_3)$. Sabemos que uma parábola interpola esses três pontos, então nosso polinômio de Lagrange se parecerá com isso:

$$L(x) = ax^2 + bx + c$$

Ainda não sabemos como calcular o polinômio interpolador, mas isso está bem por enquanto. Agora, pegue um monte de valores de $x$ e calcule $L(x)$ para cada um deles; obtemos muitos pontos que pertencem à mesma parábola.

Click to zoom

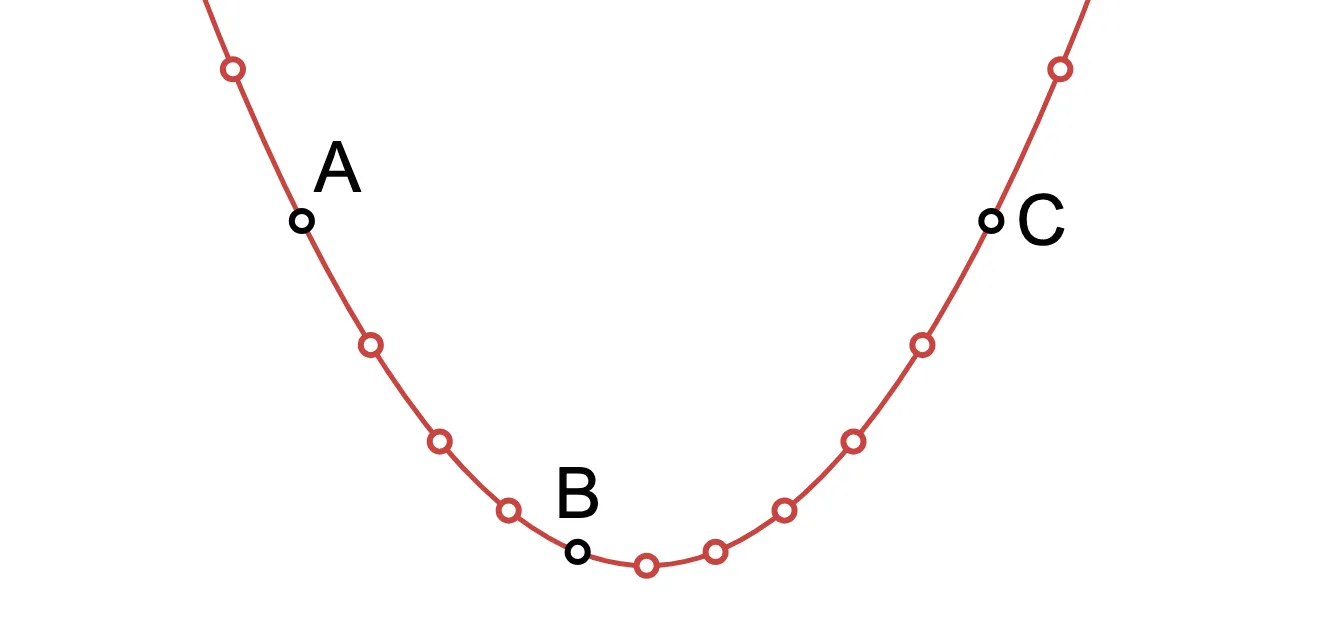
E aqui está o interessante: qualquer conjunto de três ou mais pontos do desenho anterior produz o mesmo polinômio interpolado.

E de novo, você provavelmente ainda está se perguntando "bem, mas por que preciso saber essas coisas?"

Tá bem, tá bem. Você está certo. Chega de teoria. Vamos ver como é uma aplicação, antes que eu perca seu interesse! Aqui está.

Codificação de Apagamento

Sempre que você envia um vídeo através de um aplicativo de mensagem, espera que o receptor o receba em uma única peça inalterada, certo? Mas se aprofundarmos um pouco, não é realmente assim que a informação é transmitida. Você não envia um único pacote de informação pela internet, como se fosse um pacote comprado na Amazon.

O que realmente acontece é que o vídeo original é enviado em pequenas peças, chamadas pacotes de informação. E no seu dispositivo, no dispositivo do destinatário e em muitos lugares intermediários, há processos rodando (olá, TCP) que garantem que cada pacote chegue ao seu destino, enquanto cuidam do trabalhoso processo de reconstruir o vídeo original a partir de suas peças.

E durante suas viagens, muitas vezes, os pacotes de informação se perdem ou se corrompem. Sim, você ouviu certo. E os processos que mencionamos remediam essa complicação solicitando novamente qualquer pacote perdido.

Mas há outra forma de abordar esse problema: introduzir redundância em nossos dados.

Click to zoom

Redundância significa que efetivamente vamos enviar mais informação do que realmente precisamos. Pense no nosso vídeo como algo divisível em quatro pequenos fragmentos de informação; então enviaríamos um número de fragmentos maior que quatro. E mesmo se informação for perdida no caminho, o destinatário ainda pode reconstruir os dados originais.

Mas Como?

Polinômios, é assim como.

Como sempre, tudo começa com uma ideia simples: as peças originais de dados podem ser os coeficientes de um polinômio.

$$P(x) = a_0 + a_1x + a_2x^2 + ... + a_{m-1}x^{m-1} = \sum_{i=0}^{m-1} a_ix^i$$

Cada peça de dados é apenas um número binário, ou seja, apenas um inteiro. E lembre-se, podemos reconstruir um polinômio de grau $m - 1$ a partir de pelo menos $m$ pontos (via interpolação de Lagrange). Você consegue ver como isso continua?

Só temos que avaliar $P(x)$ em $k$ pontos diferentes $x$, e requeremos que $k$ seja maior que $m$. Quantos mais, você se pergunta? Isso depende de quantos pacotes você espera perder, porque os pontos $(x, P(x))$ serão de fato os pacotes a enviar através da rede.

E é claro, o receptor pode reconstruir o polinômio original via interpolação, usando quaisquer dos $m$ pontos dos $k$ totais. E ao recuperar os coeficientes, efetivamente reconstroem a mensagem original!

Esta técnica é conhecida como códigos corretores de erros Reed-Solomon. Uma aplicação interessante para eles está nas comunicações do espaço profundo, onde ocorrem erros e corrupção de dados ao transmitir informação através de vastas distâncias. Interessante, né?

Interpolação, Revisitada

Agora conhecemos pelo menos uma aplicação para os polinômios de Lagrange. Mas ainda não sabemos como interpolar.

A forma padrão ou direta de encontrar uma interpolação polinomial é realmente bastante trabalhosa. Você encontrará expressões como esta:

$$\ell_j(x) = \prod_{\substack{0 \leq m \leq k \\ m \neq j}} (x - x_m)(x_j - x_m)^{-1}$$ $$L(x) = \sum_{j=1}^m y_j\ell_j(x)$$

Quer dizer, podemos lidar com essas equações, sem problema, mas a questão é que esta não é realmente a forma mais eficiente de interpolar um conjunto de pontos.

Para aqueles que conhecem a notação Big O, a interpolação direta resulta ser $\mathcal{O}(n^2)$. E o algoritmo mais eficiente conhecido hoje em dia, o que se apresenta a seguir, é $\mathcal{O}(n.log(n))$.

A melhor e mais rápida maneira de interpolar é usar o algoritmo da Transformada Rápida de Fourier (FFT por suas siglas em inglês). Não entraremos em detalhes sobre como isso funciona, porque envolve alguns conceitos que não introduzimos, como as raízes da unidade em um grupo.

No entanto, existem excelentes recursos se você estiver interessado em dissecar as entranhas do algoritmo. Se isso é sua praia, divirta-se!

Compartilhamento de Segredos

Finalmente, vamos ver outra aplicação, que será muito útil para projetar protocolos mais familiares como as assinaturas. Vamos dar uma olhada no Compartilhamento de Segredos de Shamir.

Lembra como o Intercâmbio de Chaves de Diffie-Hellman permitia que múltiplas partes gerassem um segredo compartilhado? Bem, tem uma limitação: o segredo é gerado.

O que isso significa é que se eu, Franco, quero revelar um valor secreto específico a um grupo de pessoas, então Diffie-Hellman não é adequado para a tarefa. Devemos pensar em outra estratégia.

E de novo, os polinômios salvam o dia. É assim como:

• Estabeleça o valor secreto $s$ como o termo independente (o coeficiente que não está multiplicado por $x$).
• Depois, selecione $m$ números aleatórios como coeficientes para um polinômio, $P(x)$.
• Para terminar, escolha $k$ valores de $x$ e avalie $y = P(x)$ em todos esses valores.

Você termina com um monte de pontos $(x, y)$. E como você sabe, qualquer conjunto de $m + 1$ desses pontos pode ser usado para reconstruir o polinômio original, $P(x)$.

Então, e agora o quê? Suponha que eu me comunico com participantes em uma rede. Compartilho $(x_1, y_1)$ com André, depois $(x_2, y_2)$ com Bruna, $(x_3, y_3)$ com Carlos, e assim por diante. Depois eles começam a se comunicar entre si: André envia $(x_1, y_1)$ para Bruna, Carlos envia $(x_3, y_3)$ para André, etc.

O que acontece é que, em algum momento, André terá peças suficientes para reconstruir o polinômio $P(x)$. E isso é legal, porque então ele olha o coeficiente independente, e esse é exatamente o segredo que eu queria compartilhar!

Este é um exemplo de um amplo conjunto de técnicas conhecidas como Computação Multi-Parte (MPC). É um tema muito interessante que expandiremos em artigos futuros.

Resumo

Curvas elípticas, hashing, polinômios: nosso conjunto de ferramentas continua crescendo! E conforme acumulamos mais ferramentas, novas técnicas criptográficas se tornam disponíveis para nós. Em particular, podemos combinar assinaturas e polinômios para produzir uma nova construção interessante: assinaturas de limite. Entraremos em detalhes no próximo artigo, esticando os limites do possível com as ferramentas atualmente à nossa disposição.