Criptografia 101 (Anexo): Avaliando Segurança

---

Este é parte de uma série de artigos sobre criptografia. Se este é o primeiro artigo que você encontra, eu recomendo começar do início da série.

Ao longo da nossa viagem, nosso objetivo sempre foi tentar entender as fundações matemáticas que sustentam a criptografia moderna. Esse é um desafio importante por si só — afinal, a criptografia é sobre criar quebra-cabeças realmente difíceis. Não há criação de nada se não podemos entender as ferramentas envolvidas.

E embora ainda haja muito para explorarmos nas formas de projetar protocolos criptográficos, acho que agora é um bom momento para fazer outro pequeno desvio, e mudar nosso foco para um aspecto que ainda não discutimos. Vamos tentar responder as seguintes perguntas:

Quão seguros são os métodos que aprendemos até agora?

O que entendemos por segurança, afinal?

Como ela é medida?

A melhor forma de responder isso, na minha humilde opinião, é fazer uma jornada rápida pela história da criptografia. Fazendo isso, vamos encontrar alguns problemas que podem comprometer a utilidade dos nossos métodos rápidamente, enquanto outros se tornarão claros mais lentamente.

E para começar, vamos voltar ao início mesmo.

A Cifra de César

A ideia de proteger dados em comunicações certamente não é nova.

Registros existem de tentativas de esconder mensagens secretas em civilizações antigas. Um exemplo famoso, e um dos primeiros usos registrados de técnicas criptográficas, é a cifra de César, que data de 100 a.C. É uma técnica muito simples: cada letra no alfabeto é deslocada um determinado número de posições. Portanto, é categorizada como uma cifra de substituição, porque cada letra é substituída por outra, seguindo um conjunto específico de regras.

Click to zoom

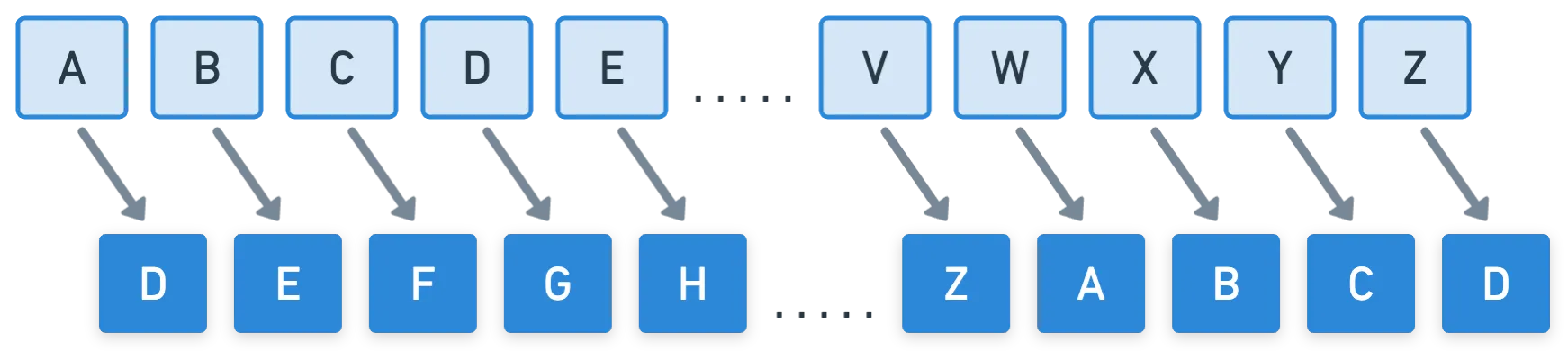
Desde que você saiba quantas posições os caracteres são deslocados, então você pode decriptar mensagens encriptadas com essa técnica. Por exemplo, se o deslocamento foi de $+3$ letras (como na imagem acima), então o texto cifrado "khooraruog" pode ser mapeado de volta ao texto original "helloworld". Poderíamos, claro, adicionar caracteres especiais, mas vamos nos ater ao método original e simples.

Tudo estava bem até que um cara chamado Al-Kindi apareceu e quebrou a cifra, façendo um exploit de uma falha fatal. Consegue adivinhar qual é?

Para ser justo, quase mil anos se passaram antes que alguém propusesse esse exploit, então não se preocupe muito se você não pegou!

O Exploit

Em qualquer idioma, algumas letras aparecem com mais frequência que outras. Se analisarmos essas frequências ao longo de uma vasta quantidade de texto, uma distribuição emergirá. Para o inglês, essa distribuição aproximadamente fica assim:

Click to zoom

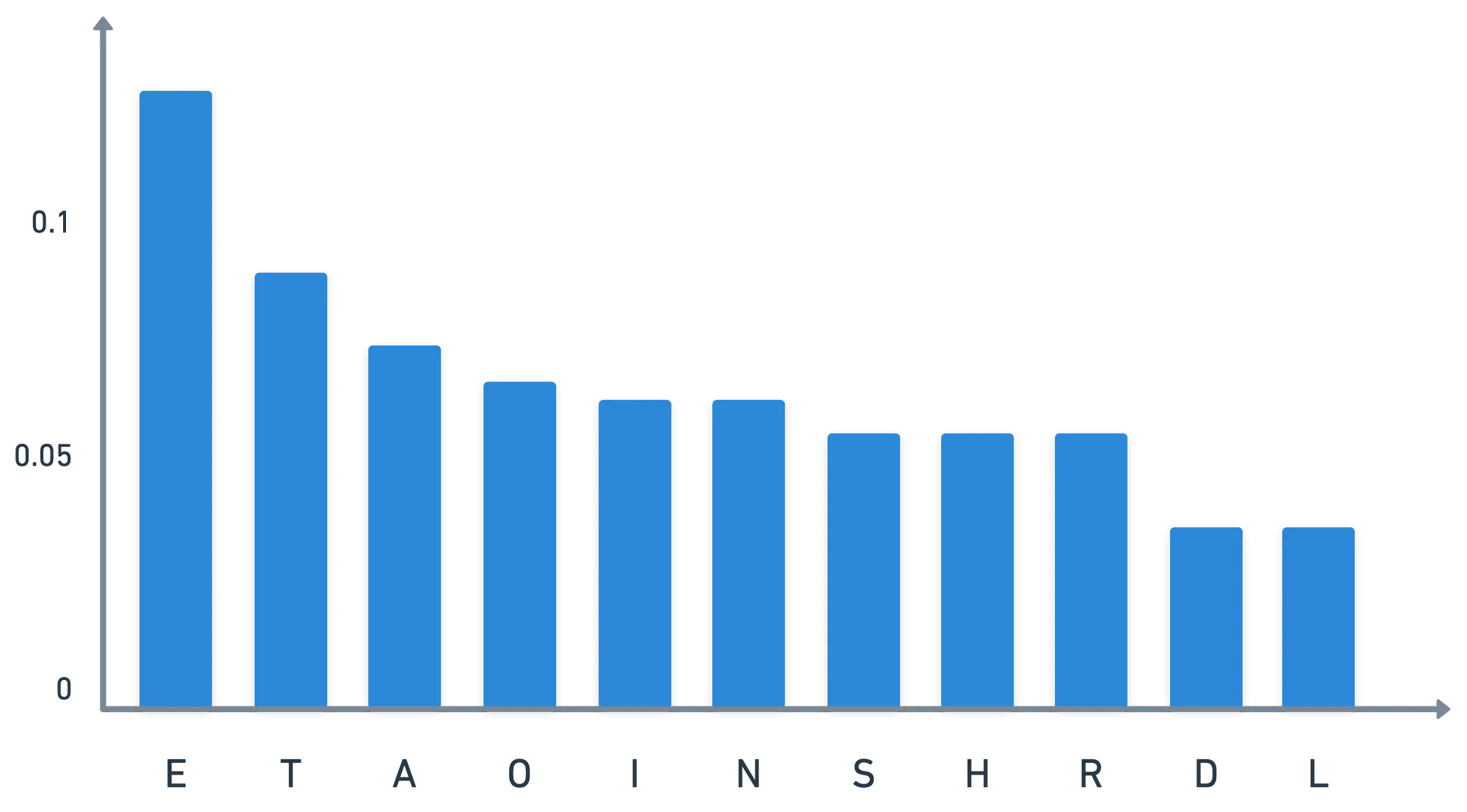
E o que podemos fazer com essa informação, você pergunta? Bem, se a mensagem por acaso for algum texto em inglês, então podemos verificar as frequências de letras na nossa mensagem encriptada. E é provável que a letra que aparece mais seja a versão encriptada da letra $E$!

Vamos ponderar isso por um minuto: por exemplo, se a letra $E$ encripta para a letra $P$, então é provável que $P$ apareça frequentemente. E as chances disso acontecer aumentam conforme o texto fica maior, porque as letras começam a se repetir.

Isso é chamado análise de frequência. E o problema realmente se resume a ter uma distribuição não-uniforme associada ao nosso texto cifrado.

Não me lembro se mencionei isso antes, mas texto cifrado (ciphertext) é uma forma como chamamos a saída de um processo de encriptação — e a entrada é frequentemente chamada texto plano (plaintext).

Consequentemente, isso significa que podemos inferir alguma informação apenas olhando para os dados encriptados. E isso é algo que nunca deveríamos poder fazer. No caso de um método de substituição "ideal", isso significaria que cada caractere é igualmente provável de aparecer no texto cifrado, o que não é o caso na cifra de César.

Em resumo, a grande ideia aqui é a seguinte:

Não deveríamos poder aprender nada dos dados encriptados olhando para o texto cifrado.

E essa é uma das grandes razões pelas quais a maioria das técnicas que vimos até agora introduz algum tipo de aleatoriedade na mistura: para tornar as coisas indistinguíveis de dados aleatórios. Isso significa que as chances de qualquer caractere aparecer no texto cifrado é quase a mesma — o que significa dizer, em termos probabilísticos, que a distribuição de caracteres é (próxima de) uniforme:

Click to zoom

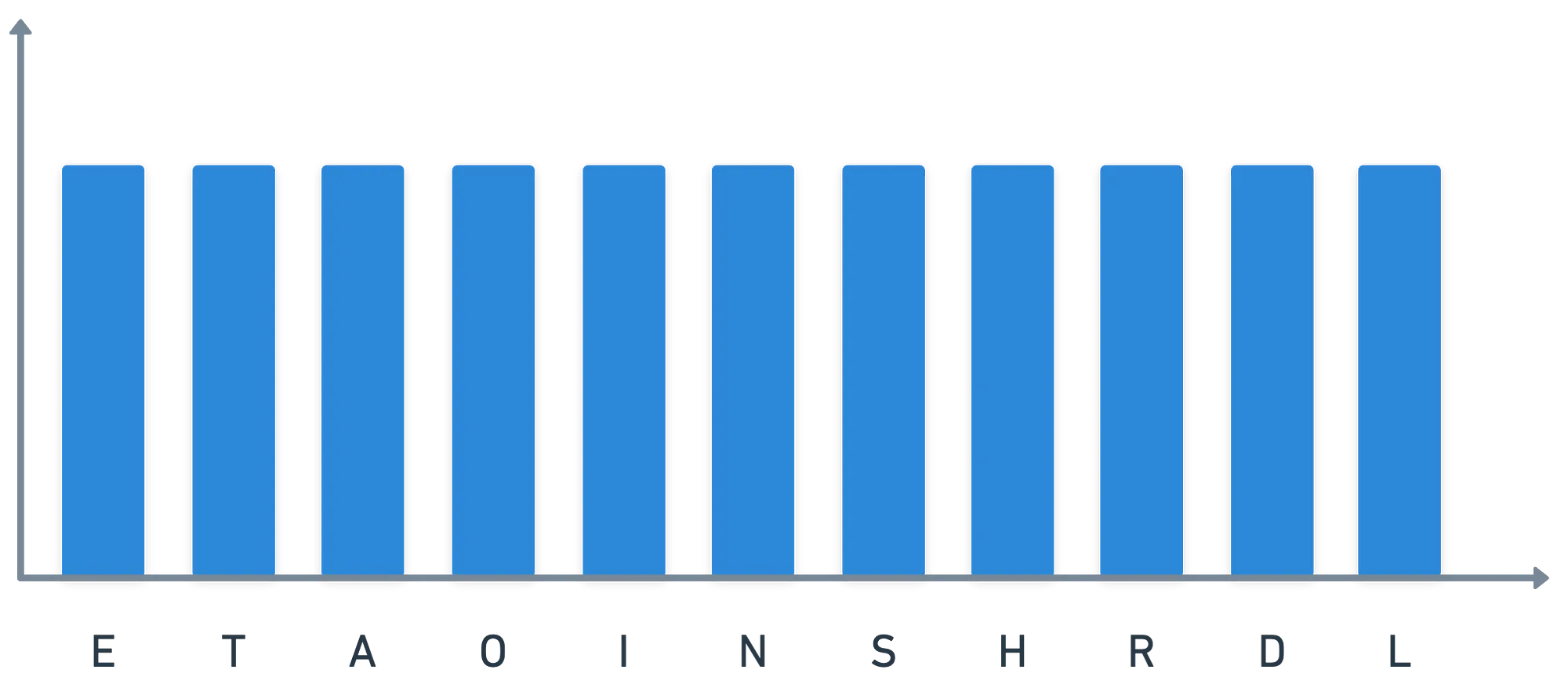
Garantido — se essa condição não for atendida, então um método provavelmente não é seguro, pois isso abre a porta para análise baseada na distribuição do texto cifrado. Tropeçamos em um requisito para segurança ao projetar métodos criptográficos.

Tamanhos de Chave

Segurança está em parte relacionada à ausência dessas backdoors ou vetores de ataque que podem comprometer nossos esforços para proteger dados, como o exemplo apresentado antes. Existem, claro, outros tipos de ataques, como ataques de texto plano escolhido, ataques de canal lateral, entre outros.

E é muito importante examinar cuidadosamente cada aspecto dos nossos métodos, pois até mesmo a menor vulnerabilidade pode quebrar tudo. Como mencionei no artigo sobre hashing, e repito agora:

Uma cadeia é tão forte quanto seu elo mais fraco

Ainda assim, vamos supor que fizemos nossa lição de casa e estamos bastante certos de que nossa técnica é muito sólida e não tem backdoors óbvias. O que mais devemos nos preocupar?

Força bruta, é isso!

A questão é simples: quão fácil seria quebrar um método criptográfico apenas por tentativa e erro? Falei brevemente sobre isso em um artigo anterior, mas agora vamos tentar quantificar essa tarefa.

Em linhas gerais, há dois ingredientes essenciais para essa questão:

• O tamanho da estrutura matemática subjacente
• A complexidade computacional das operações envolvidas no nosso problema

Por exemplo, na Criptografia de Curva Elíptica (ECC), isso significa que nos importamos com quão grande o grupo de curva elíptica é, e também nos importamos com quanto esforço computacional leva para tentar valores um por um.

Tamanhos de Chave RSA

Em vez de focar em ECC, vamos começar analisando RSA. Breve recapitulação: RSA é baseado no fato de que é difícil encontrar os dois fatores primos de um dado número $n = p.q$.

Vamos começar pequeno. Digamos que $p$ e $q$ têm no máximo $1$ byte ($8$ bits) de comprimento. Isso significa que $n = p.q$ tem no máximo $2$ bytes de comprimento. Quão difícil seria encontrar seus fatores primos?

Claro, isso seria muito fácil. Você pode tentar você mesmo com um script rápido. Para que isso seja difícil — e portanto útil para criptografia —, precisamos que $p$ e $q$ sejam muito maiores. E conforme usamos números maiores, a fatoração se torna exponencialmente mais difícil.

Nos primeiros dias do RSA, acreditava-se que usar chaves ($p$ e $q$) que tinham no máximo $512$ bits de comprimento tornaria o esquema de encriptação seguro. Mas o poder computacional só aumentou nas últimas décadas, tornando possível resolver o problema de fatoração para chaves de 512 bits em questão de dias ou até horas. Isso não parece muito seguro...

O que fazer então? Bem, aumentar os tamanhos de chave, claro! E assim, hoje em dia a recomendação é usar chaves de 2048 bits. Acredita-se que com o poder computacional disponível atualmente, ainda levaria um tempo absurdamente longo para resolver o problema de fatoração com esses tamanhos de chave. Mas isso pode mudar no futuro, conforme os computadores se tornam mais poderosos.

Computação quântica parece estar logo ali na esquina... Então, quem sabe

Tamanhos de Chave ECC

Em comparação, vamos ver o que acontece quando trabalhamos com curvas elípticas. Mencionamos como multiplicar um ponto $G$ por algum número $m$ envolve alguns passos. E isso é muito importante, porque o algoritmo de duplicar-e-adicionar tem que ser executado toda vez que tentamos um número $m$ para verificar que ele resolve o problema do logaritmo discreto:

$$Y = [m]G$$

Isto é: força bruta é muito mais computacionalmente custosa do que apenas multiplicar dois números, como é o caso do RSA — nossa estrutura subjacente é mais complexa. E, por sua vez, isso significa que podemos alcançar o mesmo nível de segurança com tamanhos de chave menores. Por exemplo, uma chave de 256 bits em ECC é aproximadamente equivalente em segurança a uma chave de 3072 bits em RSA.

O Tamanho da Chave Importa?

Ah, ótima pergunta! Há algumas coisas a considerar aqui.

Em geral, quanto maiores suas chaves ficam, mais caras suas computações se tornam. Não é a mesma coisa calcular $[10]G$ e $[1829788476189461]G$, certo? E então, embora saibamos que aumentar o tamanho da chave é bom para segurança, definitivamente não é bom para velocidade. Assim, tamanhos de chave maiores nem sempre são melhores.

Escolher o tamanho de chave correto é realmente um ato de equilíbrio. Depende do que valorizamos mais: velocidade, segurança, ou um meio-termo entre ambos.

Se não nos importamos muito com velocidade, e precisamos que nossos métodos sejam muito seguros, então chaves maiores são necessárias. Mas podemos precisar de algoritmos mais rápidos, e então reduzir os tamanhos de chave pode ser uma opção.

Resumo

Este artigo curto passa rapidamente por alguns dos aspectos mais importantes relacionados à segurança. Na realidade, este tipo de análise pertence a um ramo inteiro próprio: criptoanálise, que é uma espécie de irmã da criptografia. Seria quase desagradável para mim dizer que este é um artigo de criptoanálise — em vez disso, é uma introdução muito gentil a algumas das ideias por trás da disciplina.

Uma coisa é clara, no entanto: projetar métodos criptográficos é tão importante quanto entender como quebrá-los. Pular essa análise nos deixa em risco de criar um sistema defeituoso, que em última instância não cobre as garantias de segurança que podemos estar oferecendo aos nossos clientes — e isso não é nada bom.

Intencionalmente omiti a introdução da ideia de um parâmetro de segurança, apenas para manter as coisas simples. Você pode ver isso em artigos ou discussões técnicas, então talvez queira ler sobre isso como uma generalização de alguns dos conceitos discutidos acima.

Com isso, pelo menos temos uma ideia geral de algumas possíveis fraquezas nos nossos métodos — embora haja muito mais a cobrir nesta área. Apenas tenha sempre em mente que segurança não está associada a quão sofisticada a matemática fica. Sofisticado não é igual a seguro, e uma análise cuidadosa é sempre uma boa prática!