Criptografia 101: Esquemas de Comprometimento Revisitados

Este é parte de uma série de artigos sobre criptografia. Se este é o primeiro artigo que você encontra, eu recomendo começar do início da série.

Até agora, vimos emparelhamentos em ação, no contexto de criptografia baseada em identidade. Mas também vimos que os emparelhamentos são poderosos por si só, habilitando outros métodos que não dependem de identidade. Neste artigo, gostaria de expandir essa ideia.

É hora de revisitar um conceito de alguns artigos atrás: esquemas de comprometimento. Definimos anteriormente o que eles são: formas de se comprometer com um valor, sem revelá-lo antecipadamente.

Uma espécie de mecanismo criptográfico anti-trapaça.

Desta vez, vamos olhar para um tipo de esquema de comprometimento que ainda não mencionamos: comprometimentos polinomiais. Em particular, o método a ser apresentado é o descrito neste paper: o comprometimento KZG (Kate-Zaverucha-Goldberg).

Uma Breve Ressalva

Acredito que, neste ponto da série, seria difícil rotular artigos como sendo 101 — ou seja, eles não são mais tão introdutórios. Independentemente disso, o espírito dessas apresentações é tornar o conteúdo e a notação um tanto criptográficos dos papers um pouco mais acessíveis. Nesse sentido, é verdade que removi alguns elementos complexos — e mesmo assim, isso não significa que esses tópicos fiquem mais fáceis.

Ainda assim, se você chegou a este ponto da série, provavelmente significa que você está muito investido em entender esses conceitos criptográficos complexos. Então parabéns pelo esforço, obrigado por ler junto, e espero que você ainda ache o conteúdo útil!

Comprometendo-se a um Polinômio

Nossa descrição de esquemas de comprometimento até agora realmente só cobre o cenário onde há um valor secreto que não queremos revelar antecipadamente. E abrir o comprometimento significa revelar o valor.

Mas e se pudéssemos ter uma fábrica inteira de comprometimentos?

Ou seja, e se pudéssemos nos comprometer com uma função? Então, o que poderíamos fazer é fornecer avaliações da função a um verificador, e eles podem verificar sua avaliação correta usando nosso comprometimento.

Para ser justo, mesmo que isso soe como uma ideia interessante de perseguir, não está imediatamente claro se há alguma aplicação adequada.

Então, para mantê-los motivados, vou dizer isso: comprometer-se a uma função é um ingrediente chave em algumas Provas de Conhecimento Zero que vamos olhar em artigos futuros.

Além disso, lembre-se de que quando falamos sobre criptografia de limite, mencionamos que havia situações que requerem compartilhamento secreto verificável. Isso é, não apenas as avaliações de um certo polinômio são necessárias, mas também uma prova de sua correção.

Esquemas de comprometimento polinomial podem ajudar nesse aspecto.

O contexto está (meio que) definido. Talvez um diagrama ajude a esclarecer o que quis dizer antes:

Click to zoom

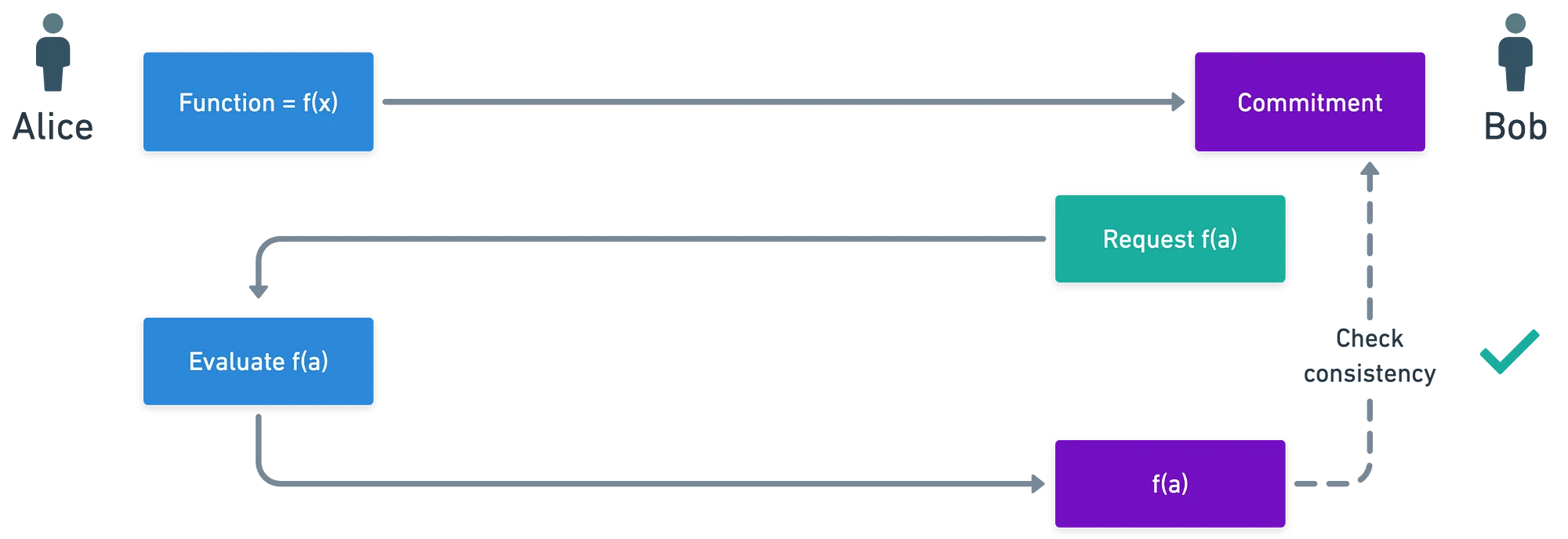
Observe que no diagrama acima, a função $f$ é secreta, e jamais realmente divulgada. E como você pode estar adivinhando agora, a verificação de consistência será feita com a ajuda de um emparelhamento.

Tendo dito isso, vamos direto ao ponto.

Configurando as Coisas

Nosso esquema de comprometimento consistirá de pelo menos três etapas. O paper em si descreve cerca de seis algoritmos, mas podemos cortar alguns cantos para tornar a explicação mais digerível.

Para começar, vamos precisar de dois grupos de ordem $n$: vamos chamá-los de $\mathbb{G}_1$ e $\mathbb{G}_3$. Também vamos precisar de um gerador para $\mathbb{G}_1$, que vamos denotar por $G$. Esses grupos são gerados de tal forma que existe um emparelhamento simétrico (ou auto-emparelhamento) da forma:

$$e: \mathbb{G}_1 \times \mathbb{G}_1 \rightarrow \mathbb{G}_3$$

E isso será uma peça crucial do quebra-cabeça para nós.

Além disso, já que vamos lidar com polinômios, desta vez vamos preferir a notação multiplicativa para representar os elementos de $\mathbb{G}_1$; isso é, o grupo terá a forma:

$$\mathbb{G}_1 = \{G^0, G^1, G^2, G^3, ..., G^{n-1}\}$$

Uma nota importante: já que $G$ será uma entrada para um polinômio, e geralmente apresentamos nossos exemplos com grupos de curvas elípticas, temos um problema: pontos em uma curva elíptica são multiplicados por um escalar (isto é, $[s]G$), e não exponenciados.

Para aliviar essa questão, podemos fazer uso de um isomorfismo em um grupo multiplicativo, com raciocínio similar ao explicado aqui.

Então realmente, $G^s$ vai significar apenas $[s]G$.

Legal, legal. Com isso podemos realmente começar a configurar as coisas.

A Configuração

Agora, este processo funciona com o que é conhecido como uma configuração confiável. Para funcionar, o sistema tem que ser inicializado, no sentido de que alguns parâmetros públicos precisam ser calculados. Esses parâmetros serão importantes durante o processo de verificação.

Vamos fazer um comprometimento a um polinômio de grau no máximo $d$. E para isso, esta é a configuração que precisamos: um ator confiável amostra um inteiro aleatório $\alpha$. Eles usam isso para calcular o seguinte conjunto de parâmetros públicos:

$$p = (H_0 = G, H_1 = G^{\alpha}, H_2 = G^{\alpha^2}, ..., H_d = G^{\alpha^d}) \in \mathbb{G}^{d+1}$$

E após obter esses valores, $\alpha$ deve ser descartado. O conhecimento de $\alpha$ permite que provas falsas sejam forjadas — e é por isso que precisamos confiar em quem executa essa ação. Vamos ver como uma prova falsa poderia ser produzida mais adiante.

Comprometendo-se ao Polinômio

Agora que todo mundo tem os parâmetros públicos $p$, podemos criar o comprometimento real.

Interessantemente, o comprometimento será um único valor funcional:

$$\tilde{f} = G^{f(\alpha)} \in \mathbb{G}$$

Vamos usar a notação til ($~$) para denotar comprometimentos a funções. Por exemplo, $\tilde{f}$ representa um comprometimento a $f$.

Ao inspecionar mais de perto, podemos ver que $\alpha$ é necessário para computar o comprometimento. Mas em teoria, $\alpha$ foi descartado neste ponto! Então como podemos possivelmente calcular isso?

Lembra dos parâmetros públicos calculados durante a configuração? É aqui que eles entram em ação. Dado que nosso polinômio tem a forma:

$$f(x) = a_0 + a_1x + a_2x^2 + ... + a_dx^d$$

O que podemos fazer é produzir o seguinte produto, usando os parâmetros públicos:

$$S = {H_0}^{a_0}.{H_1}^{a_1}.{H_2}^{a_2}....{H_d}^{a_d} = \prod_{i=0}^d {H_i}^{a_i}$$

Se trabalharmos um pouco a expressão:

$$S = G^{a_0}.G^{\alpha.a_1}.G^{\alpha^2.a_2}....G^{\alpha^d.a_d} = G^{a_0 + a_1.\alpha. + a_2\alpha^2 + ... + a_d.\alpha^d} = G^{f(\alpha)}$$

E aí está! Sem conhecimento de $\alpha$, ainda somos capazes de calcular nosso comprometimento. Este valor é calculado pelo provador, e enviado ao verificador, que vai armazenar este valor, e depois usá-lo quando tiver que verificar que avaliações posteriores do polinômio estão corretas.

Vamos ver como!

Avaliação

Com conhecimento do comprometimento, podemos pedir avaliações do polinômio secreto. Referindo-nos de volta ao nosso esboço original do processo, isso significa que um verificador quer saber o valor do polinômio secreto $f(x)$ em algum inteiro $b$ certo, então eles realmente pedem o valor $f(b)$:

$$f(b) = a_0 + a_1b + a_2b^2 + ... + a_db^d$$

O provador pode simplesmente calcular isso e enviar ao verificador, mas o verificador precisa ter certeza de que o cálculo está correto e consistente, e que não está recebendo um valor aleatório, sem sentido.

Então, junto com o valor $f(b)$, o provador vai precisar produzir uma prova curta que o verificador pode verificar contra o comprometimento que eles possuem.

Click to zoom

Vamos dar uma olhada mais de perto em como a prova é produzida.

A Prova

Rapidamente reiterando o objetivo, queremos provar que $f(b)= v$. Reorganizando as coisas um pouco, também é verdade que:

$$f(b) {-} v = 0$$

E isso significa que $b$ é uma raiz deste polinômio:

$$\hat{g}(x) = f(x) {-} v$$

Com essa simples mudança de perspectiva é o que vai nos permitir produzir a prova necessária.

Graças ao teorema do fator, sabemos que $\hat{g}$ pode ser perfeitamente dividido (sem resto) pelo polinômio $(x {-} b)$. Podemos calcular o polinômio quociente $p(x)$, que é o polinômio que satisfaz:

$$p(x)(x {-} b) = \hat{g}(x) = f(x) {-} v$$

O que acontece a seguir é que um comprometimento a $p(x)$ é calculado; isso é feito exatamente como fizemos com $f(x)$: usando os parâmetros públicos. E este comprometimento vai ser a prova curta que precisávamos. Então nosso diagrama anterior pode ser atualizado assim:

Click to zoom

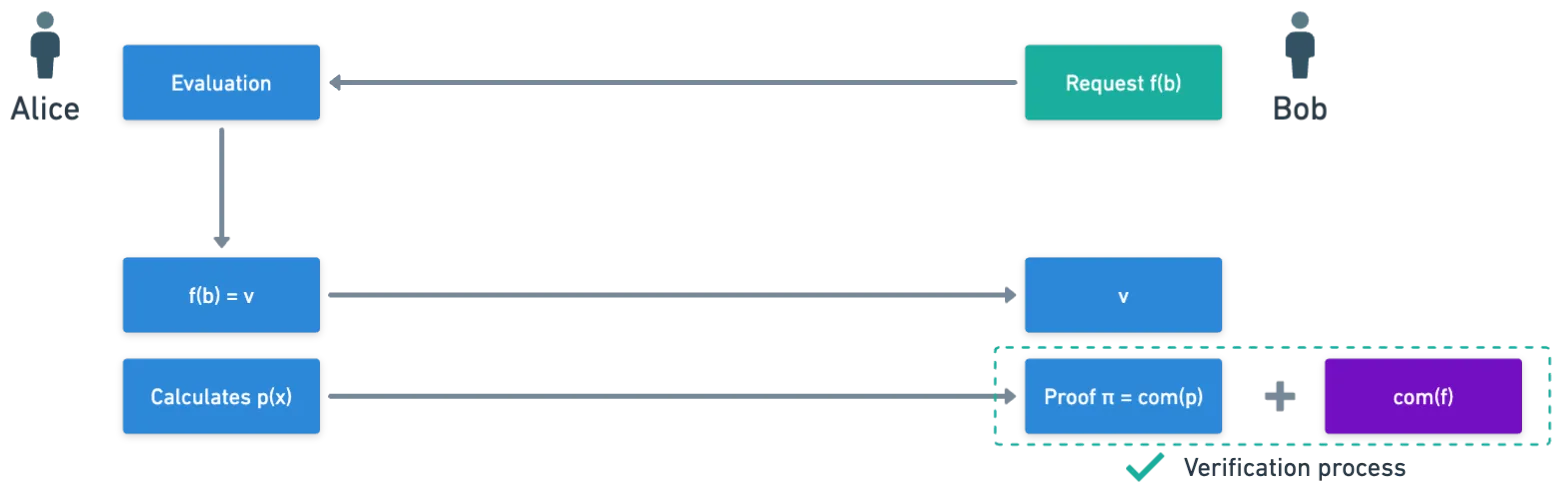
Ao receber a avaliação polinomial $v$ e o comprometimento a $p(x)$, o verificador pode verificar que esses dois valores fazem sentido. E é aqui que as coisas ficam interessantes.

Até agora, tudo bem? Isso me levou algumas leituras para entender completamente a ideia — recomendo ir devagar se necessário.

E spoilers: esta próxima parte pode ser um pouco mais pesada que o normal. Nossa. Prepare-se.

Verificação

Simplificando, o verificador só vai aceitar a avaliação se a seguinte validação acontecer de ser verdadeira:

$$\tilde{p}^{\alpha {-} b} = \tilde{f}.G^{-v}$$

Há um problema óbvio aqui: $\alpha$ foi descartado, então é desconhecido. Vamos ver como contornar essa questão em um momento. Mas primeiro, vamos ter certeza de que esta expressão faz sentido.

Lembre-se do que os comprometimentos são: dado um polinômio $f$, é apenas o valor:

$$\tilde{f} = G^{f(\alpha)} \in \mathbb{G}$$

E já vimos como calcular isso usando os parâmetros públicos. Se inserirmos isso na expressão de validação, obtemos:

$${\left ( G^{p(\alpha)} \right )}^{\alpha {-} b} = G^{f(\alpha)}.G^{-v}$$

Verificando apenas os expoentes vemos que:

$$p(\alpha)(\alpha {-} b) = f(\alpha) {-} v$$

Claro, se $p(x)$ foi calculado e avaliado corretamente, sabemos que as expressões $(\alpha {-} b).p(\alpha)$ e $(f(\alpha) {-} v)$ devem corresponder. Então o procedimento de verificação faz sentido!

É aqui que podemos visualizar claramente por que o conhecimento de $\alpha$ permite que provas falsas sejam forjadas.

Veja, eu poderia enviar a você algum número arbitrário $A$ em vez de $f(\alpha)$ como o comprometimento inicial, e você não teria como dizer que não é legítimo. Então, porque eu sei $\alpha$, eu poderia escolher algum $v$ arbitrário, e convencê-lo de que $f(b) = v$ apenas calculando diretamente e enviando a você o valor $P$:

$$P = \frac{A {-} v}{\alpha {-} b}$$

E a pior parte é, você nunca teria nem a menor pista de que as provas são falsas. Então é, é importante que $\alpha$ seja descartado!

Em conclusão, $\alpha$ permanece desconhecido. O que podemos fazer sobre isso?

Mágica de Emparelhamento

E aqui, meus amigos, é onde emparelhamentos entram. Vou apenas apresentar como o processo funciona, e vamos verificar que faz sentido. Não precisa ter muito mais motivação que isso!

Para introduzir alguma terminologia que vamos usar daqui em diante, vamos chamar o comprometimento a $p(x)$ — que está relacionado ao valor $b$ —, um testemunho. E vamos denotá-lo por $w(b)$:

$$w(b) = G^{p(\alpha)} = G^{\frac{f(\alpha) {-} f(b)}{\alpha {-} b}}$$

Agora, a ideia é que precisamos verificar que este valor é consistente com o comprometimento a $f$. E para isso, vamos precisar avaliar nosso emparelhamento, e verificar:

$$e(w(b), G^{\alpha}.G^{-b}).e(G,G)^{f(b)} = e(\tilde{f}, G)$$

Opa opa opa. Para aí, Toretto. O quê?

Ok. Vamos tentar fazer sentido disso.

A essência da questão é que ambas as avaliações vão produzir o mesmo resultado apenas se $w(b)$ foi calculado corretamente. E só pode ser calculado corretamente se o provador realmente conhece o polinômio secreto.

Lembre-se de que a notação exponencial para elementos do grupo realmente significa multiplicação (escalar) de ponto de curva elíptica.

Formalmente, podemos ver que a igualdade se mantém porque, usando a propriedade de bilinearidade de um emparelhamento:

$$e(w(b), G^{\alpha}.G^{-b}).e(G,G)^{f(b)} = e(G^{p(\alpha)}, G^{\alpha {-} b}).e(G,G)^{f(b)}$$ $$e(G,G)^{p(\alpha)(\alpha {-} b)}.e(G,G)^{f(b)} = e(G,G)^{p(\alpha)(\alpha {-} b) + f(b)}$$ $$e(G,G)^{f(\alpha)} = e(G^{f(\alpha)},G) = e(\tilde{f}, G)$$

Tire um minuto. Leia de novo. Deixe isso entrar.

Se você verificar todos os parâmetros na expansão acima, verá que os elementos na explicação "mais simples" que vimos primeiro estão misturados na mistura de avaliação de emparelhamento.

Além disso, observe que fazemos uso de $G$ e $G^{\alpha}$. Esses valores são fornecidos nos parâmetros públicos, e são de fato os dois primeiros valores: $H_0$ e $H_1$. Então esses são todos os parâmetros públicos que vamos precisar para realizar a validação!

Fantástico, né?

Resumo

Reconheço que este artigo de forma alguma foi simples de seguir. Os estimados 10 minutos de duração provavelmente pareceram uma enganação. Desculpa por isso. Tentei o meu melhor para mantê-lo simples!

Para uma visão diferente e mais interativa, sugiro verificar esta palestra por Dan Boneh. Ela não cobre a verificação de emparelhamento, mas praticamente tudo mais está incluído lá.

Então, como mencionado no início do artigo, esta construção por si só não parece oferecer aplicações interessantes prontas para uso. No entanto, vamos usar isso como base para outras construções — em particular, para construir uma família de provas de (conhecimento zero) poderosas: SNARKs.

No entanto, esse não vai ser nossa próxima parada na série. Em vez disso, vamos falar sobre um tipo diferente de provas de conhecimento zero no próximo artigo: Bulletproofs. Isso vai naturalmente nos preparar para depois passar para SNARKs. Até a próxima vez!