Las Crónicas de ZK: Extensiones Multilineales

---

En la entrega anterior, vimos nuestra primera instancia de un protocolo que hace uso de un modelo general para la computación: los circuitos.

Aunque interesante en concepto, notamos que idealmente nos gustaría probar que un cómputo, representado como un circuito, fue correctamente ejecutado — no que sabemos cuántas entradas satisfacen el circuito (recordemos que estudiamos #SAT).

La pregunta, sin embargo, es si podemos hacer eso con nuestro conocimiento actual. Y bueno... ¡No podemos!

Ciertamente, se siente como que estamos muy cerca, y para ser justos, lo estamos. Sin embargo, llegar allí requerirá usar un pequeño artilugio matemático del que no hemos hablado hasta ahora.

Aunque las cosas pueden estar un poco más pesadas del lado matemático hoy, no pierdas de vista nuestro objetivo final: ¡probar que tenemos una entrada que satisface algún circuito!

Y así, es hora de introducir un nuevo elemento en esta serie: una pequeña herramienta que será muy útil en lo que viene a continuación.

¡Vamos a la acción!

Construyendo Intuición

Durante el artículo sobre verificación de la suma, mencioné cómo $0$ y $1$ eran dos entradas especiales debido a lo fácil que era evaluar polinomios en esos puntos.

Pero seamos honestos: en la mayoría de los escenarios del mundo real, realmente no nos importan las evaluaciones en $0$ y $1$ específicamente. Son solo números como cualquier otro — no tienen ningún significado semántico inherente.

Lo mismo no aplica realmente a la satisfacibilidad de circuitos booleanos, ¡ya que las entradas son verdaderamente variables booleanas desde el principio!

Entonces, cuando la verificación de la suma nos pide verificar sumas sobre un hipercubo booleano, surge una pregunta obvia: ¿a quién le importa?

¿Cuándo necesitaríamos sumar un polinomio sobre estos puntos específicos?

La respuesta podría sorprenderte: todo el maldito tiempo. Pero para darle sentido a todo esto, necesitamos mirar esos hipercubos booleanos bajo una luz diferente.

Codificando Información

La clave de este asunto es verlos como una forma de codificar información.

Veamos un ejemplo concreto: una simple lista de números. Supongamos que tenemos una pequeña lista de cuatro valores, digamos $[2, 3, 5, 8]$. Para acceder a un valor específico de esa lista, normalmente proporcionarías un índice. Entonces, por ejemplo, para obtener el valor $5$, solicitaríamos el valor en la lista en el índice $2$.

¡Asumiendo que estamos usando indexación desde cero, por supuesto!

Ahora, acá va una observación: los índices son simplemente enteros, y todos estos tienen representaciones binarias. Es más, esta pequeña lista tiene 4 índices posibles, que se verían así en binario:

• Índice $0$ → $00$
• Índice $1$ → $01$
• Índice $2$ → $10$
• Índice $3$ → $11$

¿Ves hacia dónde voy con esto, verdad? ¡Cada índice es simplemente un punto en el hipercubo booleano $\{0,1\}^2$!

¡Misma información, diferente representación!

Con esto, podemos imaginar la acción de leer la información en nuestra lista en un índice dado como una función, donde ya podemos asumir que los índices son valores en el hipercubo (que en este caso, es solo un cuadrado booleano):

$$f: \{0,1\}^2 \rightarrow \mathbb{F}$$

Que es solo notación matemática para decir "una función $f$ que toma dos variables booleanas, y devuelve algún valor en un campo".

Entonces, siguiendo el ejemplo, tenemos:

• $f(0,0) = 2$
• $f(0,1) = 3$
• $f(1,0) = 5$
• $f(1,1) = 8$

Okay, okay. ¿Pero esto no es solo más re-etiquetar sin mucho sentido?

¡En realidad, no! Lo realmente importante aquí radica en esa pequeña función $f$ que hemos deslizado tan disimuladamente a nuestro campo visual. Implícitamente, estamos diciendo que esta función es capaz de codificar datos.

De hecho, hemos visto un método para obtener dicha función: interpolación. Obviamente, lo que obtenemos de ese proceso es un polinomio. Y es a través de este tipo de codificación que el protocolo de verificación de la suma se volverá relevante.

¡Genial! Lento pero seguro, parece que estamos llegando a algún lado.

Pero quiero que notes algo: en nuestro paso por la interpolación de Lagrange, en realidad nos enfocamos en el caso univariado. La interpolación se presentó como una forma de obtener un polinomio univariado a partir de evaluaciones, que tratamos como pares $(x, y)$.

Sin embargo, en el protocolo de verificación de la suma, hacemos uso de algún polinomio $g$ con $v$ variables, en lugar de una sola variable. Así que aquí, la interpolación como la describimos no nos llevará al tipo de polinomio que necesitamos.

Por lo tanto, vamos a necesitar algo diferente.

Extensiones Multilineales

Lo que necesitamos es una forma de ir de una función multivariada (como nuestra $f$ de arriba) definida sobre un hipercubo booleano a un polinomio multivariado. Llamaremos a dicho polinomio $g$ por conveniencia, dado nuestro paralelo con la verificación de la suma.

Y haremos esto de una manera muy especial. Porque hay dos condiciones importantes a considerar:

• Coincidencia en el hipercubo: queremos codificar algunos datos, lo que significa que $g$ debe coincidir con un conjunto de valores en el hipercubo booleano.
• Extensión más allá del hipercubo: en el protocolo de verificación de la suma, se nos requiere evaluar $g$ en puntos distintos a los del hipercubo.

Combinadas, estas dos condiciones definen precisamente el comportamiento de $g$:

Necesita ser un polinomio multivariado donde cada entrada puede ser un elemento del campo finito, y cuyas salidas coincidan con los valores codificados en el hipercubo booleano

Sí... Eso es un montón. Vamos a desglosarlo.

Primero, estamos diciendo que necesitamos alguna función definida sobre estos conjuntos:

$$g: \mathbb{F}^v \rightarrow \mathbb{F}$$

Esto es, toma $v$ entradas en el campo $\mathbb{F}$, y nos permitirá codificar un total de $2^v$ valores. Y para esos valores, tenemos una serie de restricciones a la función:

• $g(0, 0, ..., 0, 0)$ codifica $f(0, 0, ..., 0, 0) = k_0$, entonces $g(0, 0, ..., 0, 0) = k_0$, donde $k_0$ es algún elemento en $\mathbb{F}$.
• Luego, $g(0, 0, ..., 0, 1)$ codifica $f(0, 0, ..., 0, 1) = k_1$, entonces $g(0, 0, ..., 0, 1) = k_1$.
• De igual manera, $g(0, 0, ..., 1, 0) = k_2$.
• $g(0, 0, ..., 1, 1) = k_3$

Y así sucesivamente. Por lo tanto, requerimos que:

$$f(w) = g(w) \ \forall w \in \{0,1\}^v$$

Que es solo notación matemática para: $g = f$ solo en el hipercubo.

Esta es la construcción que buscamos. Es como si estuviéramos extendiendo nuestra función original $f$ para que las entradas puedan tomar valores distintos de $0$s y $1$s, permitiendo valores en el campo finito más grande. De ahí el nombre: extensiones multilineales.

Pero espera, ¿por qué multilineales? ¿Qué significa eso siquiera?

Multilinealidad

Antes de que ocurra cualquier confusión: multivariado y multilineal no son la misma cosa.

Los polinomios pueden tener, como ya sabemos, diferentes grados, ya que los diferentes términos en la expresión pueden elevarse a diferentes potencias enteras. Incluso podríamos estirar un poco el lenguaje aquí y hablar del grado de cada variable, como la máxima potencia a la que una variable dada se eleva a lo largo de toda la expresión.

Decir que un polinomio es multilineal en realidad plantea una restricción fuerte sobre cómo puede verse el mismo: lo que estamos diciendo es que el grado de cada variable es a lo sumo $1$. Para ser perfectamente claros, esto es un polinomio multilineal:

$$g(X_1, X_2, X_3, X_4) = X_1X_4 + X_2X_4 + X_3X_4$$

Y esto no lo es:

$$g'(X_1, X_2, X_3, X_4) = X_1²X_4 + X_2X_4 + X_3X_4$$

¡Ese único término con $X_1^2$ hace que todo el polinomio sea no lineal!

Bien... Pero, de nuevo, ¿por qué importa esto?

Resulta que imponer esta condición tiene un par de consecuencias interesantes. Verás, en principio, podríamos extender nuestra función original $f$ usando polinomios de cualquier grado. ¡De hecho, hay infinitas maneras de hacer esto!

Tomemos por ejemplo nuestra lista de 4 elementos $[2, 3, 5, 8]$. Podríamos construir polinomios como:

• $g_1(X_1, X_2) = 2 + X_1 + 3X_2 + X_1X_2$
• $g_2(X_1, X_2) = 2 + X_1^3 + 3X_2 + X_1X_2^5$
• $g_3(X_1, X_2) = 2 + 100X_1^7 + 3X_2 {-} 99X_1^7 + X_1X_2$

Los tres codifican correctamente la lista en $\{0,1\}^2$, y por supuesto divergen en todos los demás puntos. Entonces... ¿Qué hace que la multilinealidad sea especial, específicamente?

Primero que nada, está el hecho de que una expresión multilineal es simple y eficiente. Estos polinomios requerirán evaluación en algún momento, y en ese sentido, el grado importa. Los polinomios multilineales tienden a ser menos costosos de evaluar que expresiones de mayor grado, y además generalmente tienen menos coeficientes, lo que también impacta los costos de comunicación.

¡Además, algunos argumentos de solidez dependen de que algunos polinomios tengan bajo grado!

Pero esto no es todo. Cuando nos restringimos a polinomios multilineales, resulta que hay solo una manera de definir $g$ para que coincida con todos nuestros requisitos. En otras palabras, una extensión multilineal (o MLE por sus siglas en inglés) de alguna función $f$ definida sobre el hipercubo booleano es única.

Diablos, lo voy a repetir en términos aún más fuertes:

Hay una manera natural y única de extender una función $f$ definida en un hipercubo booleano a un polinomio multilineal

Esto es poderoso. Tanto así, que creo que deberíamos demostrar esta afirmación.

¡Siéntete libre de saltarte esta próxima sección. Solo creo que vale la pena, ya que es una propiedad tan útil de las extensiones multilineales!

Unicidad

Para mostrar esto, primero necesitaremos una estrategia para construir tal función $g$.

Esto es lo que haremos: para cada punto $w$ en $\{0,1\}^v$, construiremos un polinomio que evalúe a $1$ en $w$, y a $0$ en todos los demás puntos del hipercubo.

Eso debe sonar familiar. ¿Puedes recordar dónde vimos algo similar?

¡Sí, eso es exactamente cómo definimos las bases de Lagrange! Eso es prácticamente lo que estamos haciendo aquí.

Muy bien entonces, definamos eso:

$$\chi_w(X_1, ..., X_v) = \prod_{i=1}^{v} [w_iX_i + (1-w_i)(1-X_i)]$$

La expresión puede verse un poco extraña, pero funciona perfectamente bien:

• Cuando los valores de $X$ son las coordenadas de $w$, cada término evalúa a $w_i^2 + (1 {-} w_i)^2$. Nota que esto es igual a $1$ cuando $w_i$ es $0$ o $1$. Por lo tanto, todo el producto resulta en $1$.
• Cuando $X$ toma algún otro valor diferente de $w$, entonces al menos un $X_i$ es diferente de $w_i$, entonces o bien $X_i = 0$ y $w_i = 1$, o viceversa. En ambos casos, $w_iX_i + (1 {-} w_i)(1 {-} X_i)$ es igual a $0$, colapsando así todo el producto a $0$.

Para obtener nuestra extensión, solo necesitamos sumar todos estos términos juntos, multiplicados por el valor codificado en un índice dado, $f(w)$:

$$g(X_1, ..., X_v) = \sum_{w \in \{0,1\}^v} f(w) \chi_w(X_1,...,X_v)$$

Puedes verificar por ti mismo que esta expresión es multilineal. ¡Y como tal, hemos construido una MLE válida de $f$!

Lo que queda es probar que esta expresión es la única MLE posible para $f$.

Voy a empezar a abusar un poco de la notación ahora, para mantener las cosas un poco más condensadas. Cuando digo $p(X)$, simplemente asume que $X$ es un vector. ¡Esto tiene sentido en el contexto en el que estamos trabajando, después de todo!

Para hacer esto, haremos algo bastante inteligente. Supongamos que $p(X)$ y $q(X)$ son dos MLEs válidas para $f$. De ellas, construyamos este polinomio $h$, que también es multilineal:

$$h(X) = p(X) {-} q(X)$$

Debido a que $p(X)$ y $q(X)$ son MLEs válidas, tienen los mismos valores en el hipercubo booleano, lo que significa que esos valores serán raíces de $h(X)$.

Más comúnmente, esto se expresa como: $h(X)$ se anula en $\{0,1\}^v$.

Sin embargo, para probar que $p(X)$ y $q(X)$ son el mismo polinomio, necesitamos mostrar que $h(X)$ es idénticamente $0$ — es decir, su expresión es $h(X) = 0$.

Ahora, dado que $h(X)$ es multilineal, tiene grado a lo sumo $1$ en cada variable — por lo que su grado total es a lo sumo $v$. Como ya sabemos, un polinomio no nulo de grado $v$ puede tener a lo sumo $v$ raíces.

Pero... ¡Estamos afirmando que $h(X)$ tiene $2^v$ raíces distintas!

Eso es imposible: $2^v$ es mayor que $v$ (para cualquier $v \geq 1$). ¡A menos, por supuesto, que permitamos que $h(X)$ sea el polinomio cero!

Por lo tanto, la única posibilidad aquí es que $h(X) = 0$, lo que a su vez significa que $p(X) = q(X)$. Así, la MLE es única, y es exactamente la expresión que construimos.

¿Elegante, no?

La unicidad es importante porque previene la falsificación. Con esto, quiero decir que si existieran múltiples extensiones posibles, un probador deshonesto podría intentar construir una para satisfacer sus necesidades malignas.

Pero con las MLEs, hay solo una extensión correcta. ¡El proceso de extensión obtiene protección gratis: unicidad significa que no hay margen de maniobra para los tramposos!

Calculando MLEs

¡Muy bien! Hemos demostrado que las MLEs son únicas y están bien definidas. Pero hay algo más que necesitamos abordar: practicidad.

Echemos otro vistazo rápido a nuestra fórmula:

$$g(X_1, ... \ , X_v) = \sum_{w \in \{0,1\}^v} f(w) \chi_w(X_1, ... \ ,X_v)$$

Nota que estamos sumando sobre $2^v$ elementos, y cada uno de los términos $\chi$ involucra $v$ multiplicaciones. Ingenuamente, evaluar un solo punto en $g$ tomaría un total de $O(v.2^v)$ operaciones. Si no tenemos cuidado con cómo usamos estas extensiones, los costos computacionales podrían explotar, haciendo que las MLEs sean imprácticas.

Afortunadamente, hay una optimización inteligente para calcular MLEs que reduce dramáticamente los tiempos de evaluación, y esto es lo que finalmente hace que estos pequeños sean muy útiles.

El truco, una vez más, tiene que ver con una estructura recursiva que podemos explotar. Un ejemplo aquí ayudará a conceptualizar la idea general.

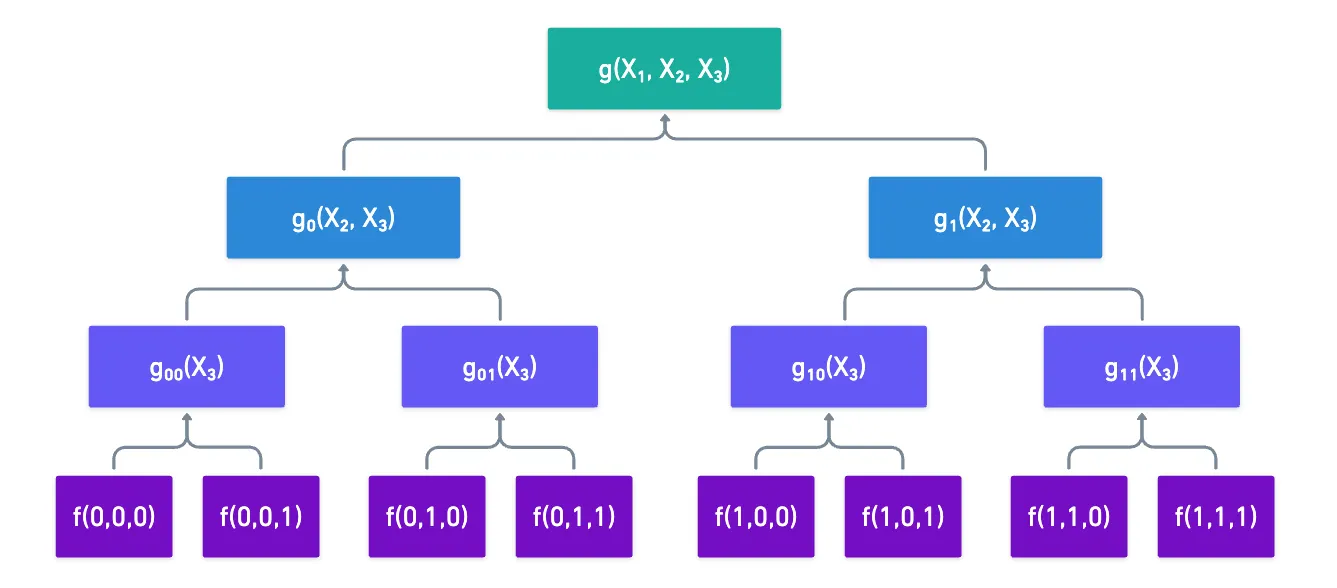
Supongamos que queremos calcular la extensión $g(X_1, X_2, X_3)$ de alguna función $f$ de 3 variables. El hecho de que cada variable sea binaria nos permite escribir $g$ de esta manera:

$$g(X_1, X_2, X_3) = (1 {-} X_1)g_0(X_2, X_3) + X_1g_1(X_2, X_3)$$

Donde $g_0$ y $g_1$ son restricciones de la función original $g$ en $X_1 = 0$ y $X_1 = 1$ respectivamente.

¡Al usar estas restricciones, hemos dividido la evaluación de nuestra MLE original en la evaluación de dos MLEs más pequeñas! Por supuesto, no necesitamos detenernos ahí: ahora podemos tomar $g_0$ y $g_1$, y hacer exactamente lo mismo, reduciendo su evaluación a dos nuevas MLEs con una variable menos.

$$g_0(X_2, X_3) = (1 {-} X_2)g_{00}(X_3) + X_2g_{01}(X_3)$$

Una vez que llegamos a polinomios univariados, su evaluación se vuelve super simple:

$$g_{01}(X_3) = (1 {-} X_3)f(0,1,0) + X_3f(0,1,1)$$

Recuerda: $X_3$, así como las otras variables, tomará valores del campo finito cuando estemos calculando la extensión multilineal — ¡no solo $0$ y $1$!

Entonces, para evaluar $g$, tenemos que ir en la dirección opuesta. Empezamos con las evaluaciones de $f$, y tomamos combinaciones de ellas. Siguiendo nuestro ejemplo resultaría en este pequeño gráfico aquí:

Click to zoom

La magia ocurre cuando consideramos el contexto en el que se usan estas MLEs. Verás, en nuestro buen protocolo de verificación de la suma, necesitamos calcular $g$ en puntos como estos en rondas subsecuentes:

• $g(0, 0, 0), g(0, 1, 0), g(0, 0, 1), g(0, 1, 1), g(1, 0, 0), ...$
• $g(r_1, 0, 0), g(r_1, 1, 0), g(r_1, 0, 1), g(r_1, 1, 1)$
• $g(r_1, r_2, 0), g(r_1, r_2, 1)$

¡Si lo necesitas, ve a revisar el protocolo de nuevo!

En cada ronda, una variable se fija a un valor de desafío $r$, pero las variables restantes aún toman combinaciones booleanas que se repiten, y pueden ser reutilizadas.

Podemos ver esto en acción en nuestro pequeño ejemplo. Supongamos que necesitamos encontrar $g(0,0,0)$, y luego $g(r_1,0,0)$. La primera evaluación nos lleva a calcular $g_0(0,0)$ y $g_1(0,0)$:

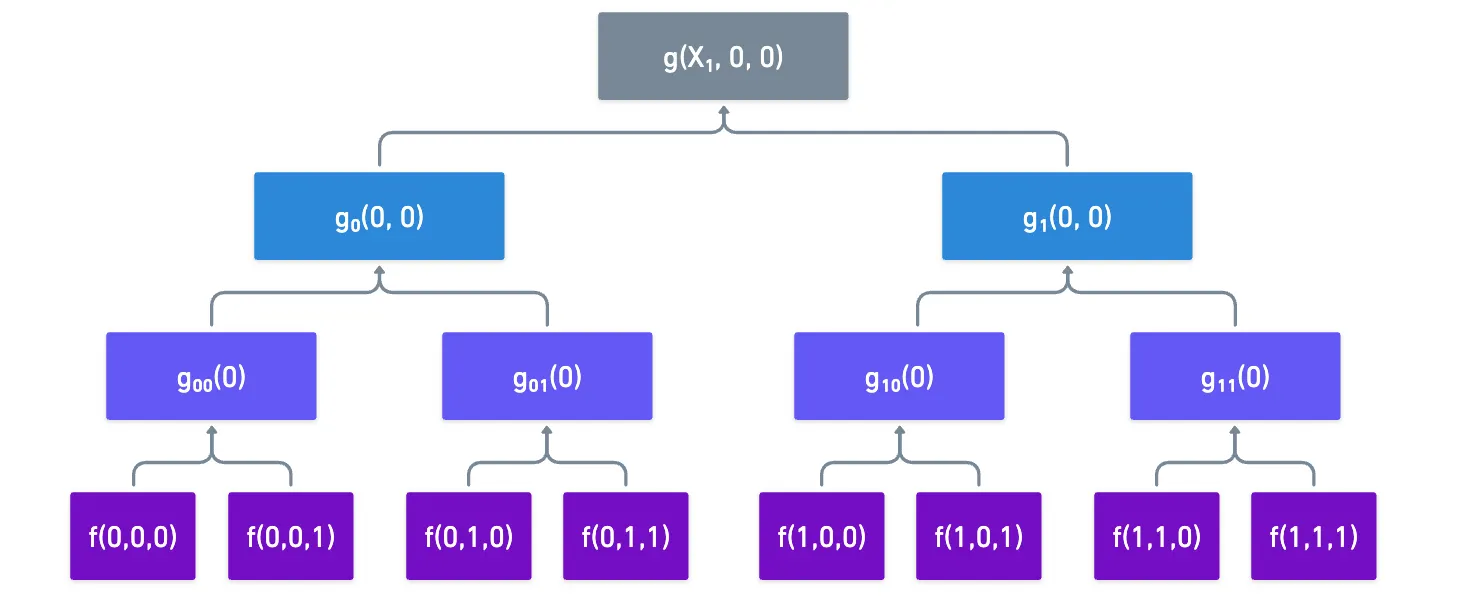
Si almacenamos esos valores para uso posterior, simplemente podemos reutilizarlos cuando se nos requiera calcular $g(r_1,0,0)$:

$$g(r_1) = (1 -r_1)g_0(0,0) + r_1g_1(0,0)$$

¡Lo que hemos hecho es usar uno de los trucos más antiguos del libro en diseño de algoritmos: memoización!

¡Todo lo que hacemos es almacenar valores intermedios cuando ejecutamos las evaluaciones completas al principio de la verificación de la suma, y luego simplemente los reutilizamos después, reduciendo significativamente los costos de evaluación!

Esta eficiencia ganada principalmente ayuda a mantener manejable el tiempo de ejecución del probador durante el protocolo de verificación de la suma, o realmente, en cualquier otro contexto donde codifiquemos datos de esta manera binaria.

¡Genial! Ahora hemos cubierto la mayoría de los trucos detrás de las MLEs. Pero antes de irnos, necesitaremos hablar de una cosa más, que resulta ser un fundamento que usaremos mucho de aquí en adelante.

El Lema de Schwartz-Zippel

La intuición que usamos hace un momento para probar la unicidad — que un polinomio no nulo de grado $d$ puede tener a lo sumo $d$ raíces — es en realidad un caso especial de un resultado más general y poderoso que usaremos muchas veces a lo largo de la serie, llamado el lema de Schwartz-Zippel. ¡Y ahora es el momento perfecto para presentarlo!

Esta es la idea: si $p(X_1, ..., X_v)$ es un polinomio no nulo de grado total $d$ sobre un campo $\mathbb{F}$, y elegimos valores aleatorios $r_1$, $r_2$, ..., $r_v$ de $\mathbb{F}$, ¿cuál es la probabilidad de que caigamos en una raíz?

Este valor resulta ser exactamente:

$$\textrm{Pr}[p(r_1, ..., r_v) = 0] \leq d / |\mathbb{F}|$$

Mientras $d$ sea mucho más pequeño que el tamaño del campo finito, ¡entonces esta probabilidad es despreciable! Así, si elegimos un conjunto aleatorio de entradas, y realmente obtenemos $p(r_1, ..., r_v) = 0$, ¡entonces hay una probabilidad muy alta de que el polinomio original fuera el polinomio constante $p(X_1, ..., X_v) = 0$!

Esto parece simple, pero en realidad es una herramienta super poderosa. Una aplicación muy simple es mostrar que dos polinomios son idénticos: dados $p(X)$ y $q(X)$, podemos definir $h(X)$ como:

$$h(X) = p(X) {-} q(X)$$

Cuando seleccionamos un punto aleatorio $r^*$, y verificamos que $p(r^*) = q(r^*)$, de hecho estamos diciendo que $h(r^*) = 0$, lo que significa con alta probabilidad que $p(X)$ es igual a $q(X)$.

¡Esto debería recordarte mucho al razonamiento que usamos durante el análisis de solidez del protocolo de verificación de la suma. Aunque no lo dijimos explícitamente, ¡usamos el lema de Schwartz-Zippel!

¡Usaremos esto mucho, así que definitivamente tenlo en mente!

Resumen

¡Muy bien, eso fue probablemente mucho! Hagamos un balance de lo que hemos aprendido hoy.

Primero, el hipercubo booleano funciona bien como una estrategia de indexación. Podríamos aprovecharlo para codificar información, ya que el índice podría servir como una entrada de alguna función, y los datos que queríamos codificar podrían ser su salida.

Luego, para usar esta función en la verificación de la suma, identificamos que necesitaba ser extendida. Así es como llegamos a las extensiones multilineales: extensiones únicas de estas funciones que ya no están limitadas a un hipercubo booleano.

Aunque no lo mencioné explícitamente, es muy fácil construir estas MLEs. Las bases de Lagrange que usamos son super simples. ¡Por esta razón, las MLEs son la opción superior al extender funciones!

Con las MLEs, podemos tomar prácticamente cualquier conjunto de datos — una base de datos, un vector, una matriz — y codificarlo como un polinomio que puede de alguna manera funcionar bien con verificaciones de la suma.

Obviamente, hay algo que no hemos abordado aún: ¿qué papel juegan las verificaciones de la suma en todo esto?

Quiero decir, codificar datos está bien y todo, pero ¿dónde está la computación?

Ahí es donde entran los circuitos. ¡Y ese será nuestro próximo destino, donde las cosas finalmente empezarán a encajar!

¡Nos vemos en la próxima!