Las Crónicas de ZK: Fundamentos Matemáticos

---

Habiendo dejado atrás la introducción a la serie, ahora es momento de empezar a trabajar en nuestro conjunto de herramientas, para que podamos encaminarnos hacia el objetivo de crear estos sistemas de pruebas a los que ya hemos aludido.

Sinceramente espero que el artículo anterior no haya sido demasiado aterrador. Para compensarlo un poquito, diré que los conceptos que veremos hoy no son demasiado complicados, mientras que al mismo tiempo tienen el beneficio adicional de ser bastante fundamentales para cualquier criptografía seria.

¡No me digas que no es una buena oferta!

Sin embargo, es importante aclarar: a medida que avancemos más en nuestro viaje juntos, necesitaremos aún más herramientas. Por supuesto, hablaremos de ellas a su debido tiempo — pero simplemente no quiero que te vayas creyendo que este artículo es suficiente preparación para el resto del camino.

Con eso, ¡el contexto está claramente establecido! Entonces, ¿por dónde empezamos?

Campos Finitos

En criptografía, la precisión es de suma importancia.

Lo que quiero decir con esto es que los algoritmos necesitan ser consistentes. Solo imagina una firma digital que funcione solo ocasionalmente — creo que estarías de acuerdo conmigo en que sería un algoritmo de m*erda (perdón por mi francés).

Por lo tanto, nuestras unidades básicas de información, o la forma en que representamos las cosas de aquí en adelante, deben ser tales que evitemos pequeños errores en las operaciones que podrían explotar si se dejan sin mucho control.

Si nos ponemos realmente exigentes acá, esto no es totalmente cierto — algunos métodos basados en el problema de aprendizaje con errores admiten pequeños errores, pero aún funcionan bien porque los mismos no solo son esperados, sino que se compensan con técnicas especiales.

Los enteros son bastante buenos en eso: al evitar operaciones de punto flotante, mantenemos las cosas limpias y consistentes. No debería sorprendernos entonces que la estructura más fundamental sobre la que construiremos sea un conjunto de enteros: lo que llamamos un campo finito.

Más estrictamente, un campo (o cuerpo) se define como un conjunto de elementos, para el cual podemos definir cuatro operaciones: adición, sustracción, multiplicación y división (excepto por cero o elementos similares a cero).

Esto debería sonar familiar — ¡los números reales que conocemos y amamos son un campo!

Cuando digo "podemos definir", quiero decir que tenemos reglas claras para realizar las cuatro operaciones, y que el resultado de ellas también debe ser parte del campo. Es decir, imaginamos el conjunto como nuestro universo de posibilidades: cualquier cosa que no sea parte del conjunto simplemente no existe para nosotros. Esto tendrá más sentido en un momento.

A veces requerimos la adición de un elemento extra (al conjunto). Este es un concepto útil pero más avanzado, llamado extensiones de campo.

Un campo finito es simplemente un campo con un conjunto finito de elementos. Es decir, algo como esto:

$$\mathbb{F}_5 = \{0,1,2,3,4\}$$

Algunas preguntas deberían venirnos a la mente inmediatamente después de ver esa expresión. Por ejemplo, $2 + 3 = 5$ no es parte del conjunto. ¿Qué sucede entonces?

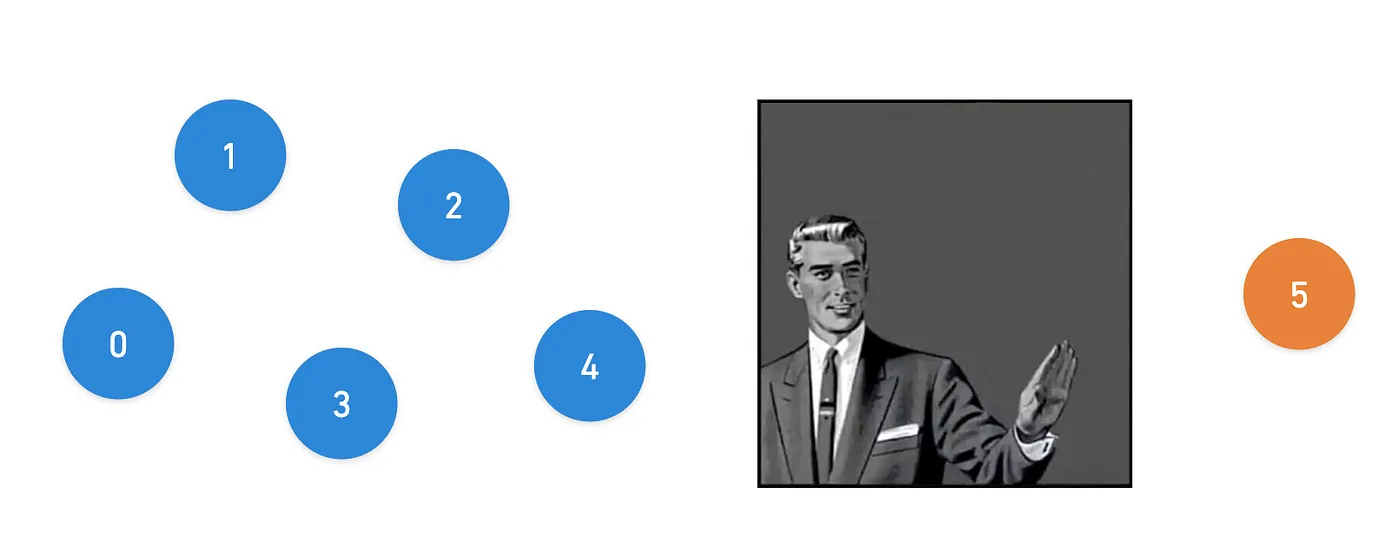
Esto es exactamente lo que quise decir antes: la adición no está bien definida, así que tendríamos que "extender" nuestro campo para incluir el nuevo elemento. Algo similar sucede con las otras operaciones.

Si tuviéramos que agregar un nuevo elemento por cada resultado posible, ¡nuestro conjunto simplemente crecería infinitamente! Así que parece que ya nos estamos metiendo en un lío desde el principio...

No te preocupes, mi joven Padawan. Dije que estas cuatro operaciones tienen que estar definidas, ¡pero nunca dije cómo!

Como las operaciones estándar no parecen funcionar en este contexto, necesitaremos descubrir otras formas de definir la adición, sustracción, multiplicación y división. De hecho, hay múltiples formas de hacer esto — pero hay una en particular que parece la más naturalmente adecuada para nuestras necesidades.

Aritmética Modular

Todo lo que tenemos que hacer es usar las operaciones estándar, y luego pasar el resultado a través de la operación módulo:

$$2.3 \ \textrm{mod} \ 5 = 6 \ \textrm{mod} \ 5 = 1$$

Nada demasiado elegante, ¿eh?

Esto funciona porque la operación módulo proyecta todos los resultados en nuestro conjunto original, incluso números negativos. Todo lo que necesitamos hacer es tomar los resultados módulo $p$, el tamaño del campo. En el ejemplo anterior, este número es por supuesto $5$.

Sin embargo, queda un pequeño problema: ¿qué hay de la división? Las fracciones no están permitidas en nuestros campos finitos, porque ni siquiera tenemos noción alguna de fracciones en nuestro conjunto.

Esto requerirá un pequeño cambio de perspectiva. Verás, cualquier división puede interpretarse de una manera alternativa: multiplicación por un recíproco.

Un ejemplo rápido ayudará aquí: dividir $3$ por $2$ (así $3 / 2$) es exactamente lo mismo que multiplicar $3$ por $0.5$. En este caso, $0.5$ es el recíproco de $2$ — y podemos escribirlo como $2^{-1}$.

Como mencioné antes, la noción de un recíproco no tiene sentido en nuestro contexto, porque las fracciones no están permitidas.

Pero, no todo está perdido — hay una idea importante que podemos llevarnos de los recíprocos, que nos dará pistas sobre cómo abordar este problema. Concretamente, cualquier número $a$ (excepto $0$) y su recíproco $a^{-1}$ satisfacen esta relación:

$$a.a^{-1} = 1$$

Así que acá va: para cada elemento $m$ en nuestro campo, ¿es posible encontrar algún número $m^{-1}$ que cuando se multiplique por $m$ (módulo $p$), resulte en $1$?

¡Por supuesto, excluyendo $0$!

Curiosamente, la respuesta depende del valor de $p$. Si tal número existe, se llama el inverso modular de $m$ sobre $p$, y la condición para su existencia es que $m$ y $p$ sean coprimos.

Los números coprimos son simplemente un nombre elegante para describir dos números que no comparten factores — esto es, su máximo común divisor es $1$.

Aquí hay otra pequeña perspicacia: cuando $p$ en sí mismo es primo, cada entero no negativo menor que $p$ (excepto $0$) es coprimo con él. En otras palabras, todos los elementos en nuestro conjunto $\mathbb{F}_p$ tendrán un inverso, lo cual a su vez implica que podemos definir la división para todo el conjunto.

Y con eso, todas las operaciones requeridas están definidas, ¡así que nuestros campos finitos están listos para funcionar!

¿Qué podemos hacer con ellos?

Polinomios

Bueno, ¡bastante en realidad!

Para nuestros propósitos, quizás lo más importante que podemos hacer es construir polinomios sobre campos finitos — y los polinomios, como veremos más adelante, son la salsa secreta detrás de los sistemas de prueba modernos.

Un polinomio es una expresión, que tiene una o más variables, y solo puede involucrar algunas operaciones simples: adición, sustracción, multiplicación y exponenciación (usando potencias enteras no negativas). Algo que podría verse así:

$$P(X,Y,Z) = X^2Y + 5YZ + Z^2 + 8X + 1$$

Como podemos ver, cada término está compuesto por la multiplicación de variables elevadas a alguna potencia (que si no es explícita, es solo un $1$), y otro número "simple" que llamamos coeficiente. De nuevo, si el coeficiente no es explícito, simplemente significa que su valor es $1$.

También necesitamos definir el grado de un polinomio: es la suma más alta de exponentes en cualquier término individual. En nuestro ejemplo anterior, el término $X^2Y$ tiene grado $3$ (ya que $2 + 1 = 3$), y ese es el grado más alto de cualquier término, así que $P$ tiene grado $3$.

Antes, mencioné que los polinomios se construyen solo con adición, sustracción y multiplicación — así que asumimos que los valores representados por las variables admiten estas operaciones. Es decir, estamos asumiendo, por ejemplo, que multiplicar $x \cdot y$ es válido. ¿Te suena esto?

¡Correcto! Suena mucho a campos, así que parecen tener algo que ver con todo esto. Y por supuesto, los polinomios tienen que estar definidos sobre algún campo.

Es más, si elegimos un campo finito, lo que significa que solo usamos elementos del campo como coeficientes, y restringimos los valores de las variables al campo finito también, entonces la salida del polinomio también pertenecerá al campo.

El conjunto de polinomios definidos sobre algún campo $\mathbb{F}$ usualmente se denota $\mathbb{F}[X]$.

Esto es bastante conveniente. Podemos usar nuestros campos finitos previamente definidos prácticamente sin cambios — así que esto realmente parece ser terreno fértil sobre el cual construir cosas.

Los polinomios tienen innumerables aplicaciones. Los usaremos principalmente como bloques de construcción, debido a dos áreas en las que son muy buenos: representar cómputos y codificar información.

Y lo sé — todas estas definiciones se sentirán un poco abstractas por sí solas. Así que abordemos esta siguiente parte a través de una mirada más práctica.

Codificando Información

Una de mis afirmaciones anteriores fue que los polinomios eran buenos para codificar información — ¿pero cómo puede ser eso? Después de todo, son solo expresiones que podemos evaluar. ¿De qué sirve eso para codificar?

Lo creas o no, el secreto yace en un sospechoso inesperado: los coeficientes.

Enfoquémonos en los polinomios univariados por un segundo. Listar los coeficientes de los diferentes términos (digamos de grado más alto a más bajo) resulta en una lista de elementos de campo — en otras palabras, un vector de enteros.

Olvida los polinomios por un momento: ¡un vector de enteros puede representar casi cualquier tipo de información! Es más, imagina que nuestro campo es $\mathbb{F}_2$, así que solo tenemos $0$ y $1$ disponibles. ¡Eso es exactamente lenguaje de máquina — cadenas de $0$s y $1$s!

Okay, eso es genial... ¿Pero por qué no usar vectores directamente? La única razón por la que querríamos interpretar estos vectores como polinomios es si hubiera algo para ganar al hacerlo.

Y de hecho, lo hay.

Interpolación

He hablado de esto en una publicación anterior. ¡Te recomiendo echarle un vistazo para una guía más paso a paso!

Tomemos algún polinomio $P(X)$ en $\mathbb{F}[X]$. Digamos que elegimos algunos puntos $x_1$, $x_2$, y así sucesivamente, hasta que tengamos $n$ puntos (así que llegamos a $x_n$). Cuando evaluamos el polinomio $P(X)$ en estos puntos, simplemente obtenemos un montón de elementos de campo — uno para cada entrada diferente.

$$P(x_1) = y_1, \ P(x_2) = y_2, \ ... \ P(x_n) = y_n$$

Llamamos a los pares evaluaciones o puntos de evaluación de $P$. Aunque, la terminología a veces se usa de manera bastante laxa, y "evaluaciones" podría referirse solo a los resultados. Además, nota la notación: las variables se escriben en mayúsculas, mientras que las evaluaciones son minúsculas. ¡Este será el caso para el resto de la serie!

Okay, genial, evaluar parece fácil, así que acá va una pregunta más complicada: ¿podemos ir en el otro sentido?

Esto es: dado un montón de evaluaciones $(x_1, y_1)$ hasta $(x_n, y_n)$, se puede encontrar el polinomio que generó dichos puntos?

Sí que podemos. El proceso se llama interpolación (o interpolación de Lagrange), y es extremadamente útil. Siempre y cuando estemos atentos a un par de detalles.

Veamos. Un polinomio de grado uno es simplemente una línea:

$$P(X) = mX + n$$

Quiz rápido: ¿cuántos puntos se necesitan para definir una línea?

Necesitamos al menos dos puntos. De hecho, si tenemos más puntos, necesitan estar alineados, o de lo contrario no definirían una línea, sino alguna otra función.

Click to zoom

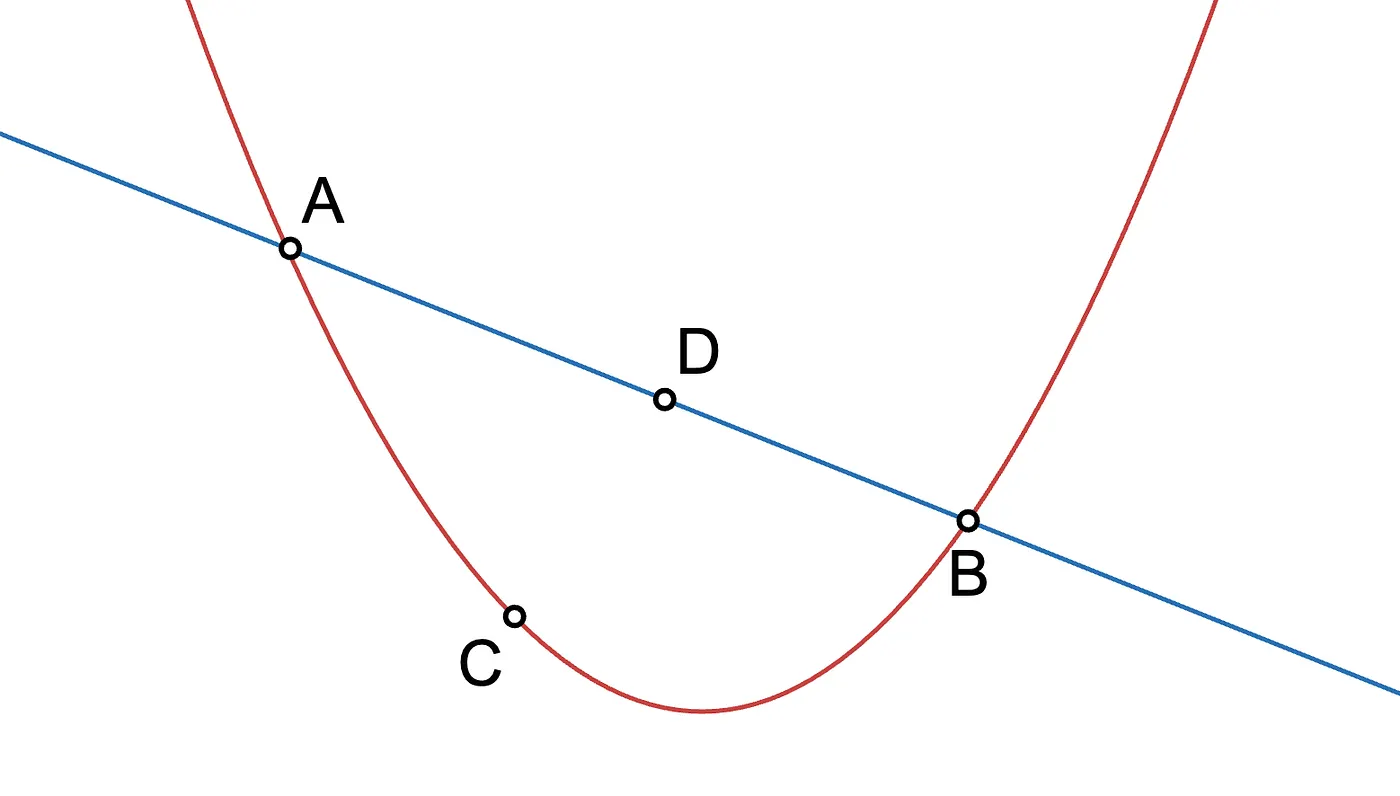
En el ejemplo anterior, está claro que interpolar tres puntos produce un polinomio de grado a lo sumo dos (una parábola), pero también podría ser de grado uno si los puntos están alineados, o grado cero si están alineados verticalmente.

Esto se generaliza muy bien a lo siguiente:

Interpolar $N$ puntos produce un polinomio de grado a lo sumo $N {-} 1$

Inversamente, necesitamos al menos $N$ puntos para codificar correctamente un polinomio de grado $N {-} 1$. Y esto tiene la siguiente implicación increíble: si tomamos cualquier polinomio univariado de grado $N {-} 1$, podemos codificarlo evaluándolo en $N$ o más puntos. Y luego, ¡cualquiera que reciba esos $N$ (o más) puntos podría recalcular el polinomio original a través de la interpolación!

¡Así que de cierta manera, tener un montón de evaluaciones polinomiales es una forma alternativa de representar algún polinomio!

Ahora deberías poder responder esto muy fácilmente:

Eso está todo bien muy bien — pero ¿cómo interpolamos realmente?

Polinomios de Lagrange

Aunque hay formas más rápidas de hacer esto (a través de la Transformada Rápida de Fourier), el método canónico es muy inteligente, y también proporciona algunas buenas perspectivas. Así que veamos eso.

La idea es la siguiente: supongamos que tenemos un conjunto de $N$ evaluaciones. Para una sola de esas, digamos $(x_i, y_i)$, podemos construir algún polinomio especial que tendrá un valor de $0$ para todos los valores $x$ excepto $x_i$, y exactamente el valor $1$ para $x_i$. Llamemos a ese polinomio $L_i(X)$.

Es como si estuviéramos "seleccionando" $x_i$ matemáticamente usando $L_i(X)$.

¿Por qué haríamos esto? Piénsalo de esta manera: si multiplicamos tal polinomio por $y_i$, entonces acabamos de fabricar una pequeña función tal que:

$$f(x_i) = y_i L_i(x_i) = y_i"$$

Como $(x_i, y_i)$ es una evaluación del polinomio original, lo que queremos obtener del proceso de interpolación es un polinomio $L(X)$ tal que $L(x_i) = y_i$ para todas nuestras evaluaciones — así que parece que $L_i(X)$ nos deja a medio camino.

Para obtener nuestro polinomio interpolado, todo lo que necesitamos hacer es sumar todos los valores de $L_i$ para todas nuestras evaluaciones:

$$L(X) = \sum_{i=1}^{n} y_i L_i(X)"$$

¡Y voilà! Ese será el resultado de nuestra interpolación. Visualmente:

Click to zoom

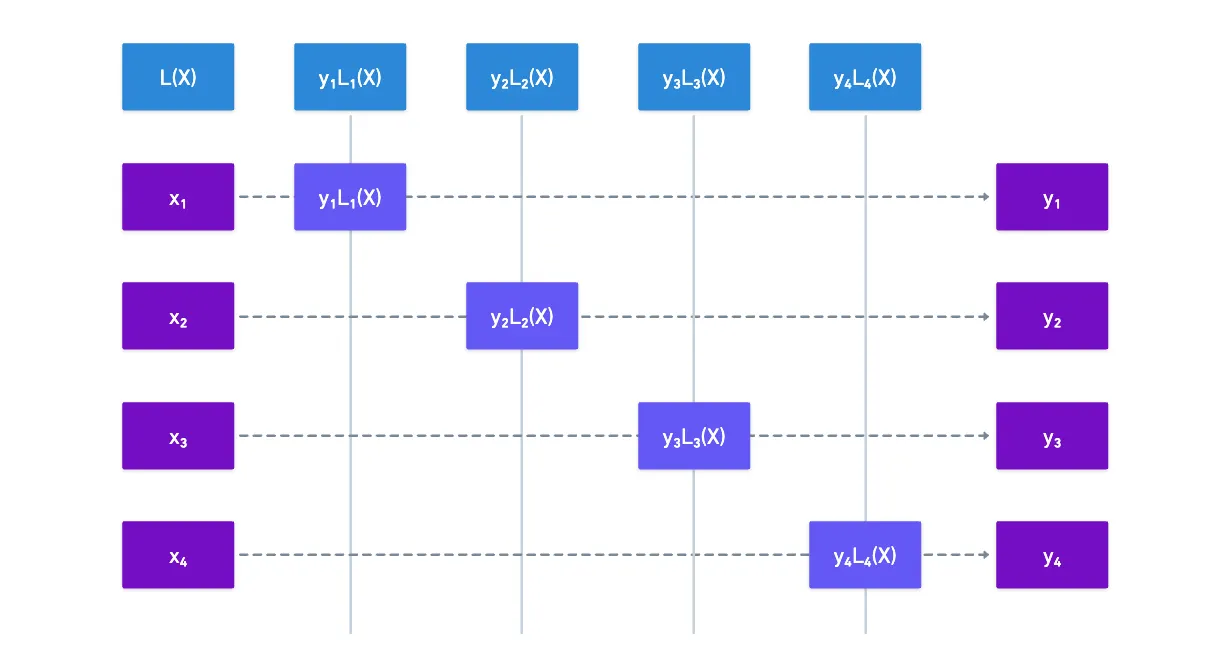
Todo lo que queda para atar bien todo es determinar cómo se definen esos $L_i(X)$.

Raíces

Recapitulemos nuestro requisito rápidamente: cada $L_i(X)$ necesitaba igualar $1$ cuando se evalúa en $x_i$, y $0$ en todas las demás evaluaciones.

Un polinomio evaluándose a $0$ es algo así como una ocurrencia especial. Tanto es así, que le damos a estos valores un nombre especial: cualquier valor $x$ tal que $P(x) = 0$ se llama una raíz del polinomio.

A pesar de su aparente simplicidad, las raíces son muy poderosas. La razón principal de esto es la existencia de un teorema importante, llamado el Teorema Fundamental del Álgebra.

Como regla general, cuando veas algo llamado "fundamental" en matemáticas, normalmente se trata de algo seriamente importante.

Simplificando un poco, una de las consecuencias más importantes de este teorema es que cualquier polinomio univariado puede expresarse como un producto de factores lineales:

$$P(X) = a(X {-} r_1)(X {-} r_2)...(X {-} r_n) = a\prod_{i=1}^{n}(X-r_i)"$$

Una observación muy importante sigue de esta expresión: un polinomio de grado $N$ tiene a lo sumo $N$ raíces. Este es un lema tan importante que no está de más repetirlo, para algo de efecto dramático:

Un polinomio de grado $N$ tiene a lo sumo $N$ raíces

Este hecho es extremadamente importante, y resulta en algunas de las herramientas más poderosas a nuestra disposición. Vamos a dejar esto en espera por ahora, pero ten en cuenta que volveremos a esto muy pronto.

Ahora, volviendo a la interpolación, resulta que esta forma es bastante útil. Está claro que cuando evaluamos cualquiera de esos valores $r_i$, obtendremos $P(x_i) = 0$. Podemos usar esto a nuestro favor aquí: los polinomios $L_i(X)$ necesitan ser $0$ en todos los valores $x$ excepto $x_i$, ¡lo que significa que son raíces de $L_i(X)$! Por lo tanto, podemos construir $L_i(X)$ como:

$$L_i(X) = a_i\prod_{\stackrel{j=1}{i \neq j}}^{n} (X {-} x_j)"$$

Estamos intencionalmente omitiendo $x_i$ para que no sea una raíz del polinomio resultante.

¡Fantástico! El único detalle que nos falta ahora es ajustar ese coeficiente $a_i$ para que obtengamos exactamente $L_i(X) = y_i$. Una simple normalización de la expresión servirá: toma cualquier valor que $L_i(X)$ produzca en $x_i$, y divide toda la expresión por eso mismo. De esta manera, al evaluar $L_i(x_i)$, simplemente obtenemos $1$.

La expresión completa es entonces:

$$L_i(X) = \frac{\prod_{i \neq j} (X {-} x_j)}{\prod_{i \neq j} (x_i {-} x_j)}"$$

¡Y eso es prácticamente todo!

El conjunto de estos polinomios $L_i(X)$ se llama una base de Lagrange. Podríamos necesitar profundizar más en lo que significa este nombre más adelante, pero por ahora, ¡el nombre debería ser suficiente para referencia!

Resumen

¡Muy bien! Eso va a ser todo por hoy.

Lo que tenemos por ahora puede parecer un poco... Decepcionante. Quiero decir, todo lo que tenemos son números y expresiones — y estas cosas probablemente se sienten un poco básicas.

Ciertamente, hay muchas capas de complejidad que podríamos explorar sobre estos elementos aparentemente simples que hemos visto hasta ahora. Pero no creo que sea práctico o instructivo hacerlo ahora.

En cambio, será mejor comenzar a explorar las aplicaciones que hacen uso de estos conceptos. A medida que comencemos a usar estas herramientas, su potencial comenzará a volverse más aparente.

Así que en nuestro próximo encuentro, estaremos viendo uno de los protocolos más simples pero más fundamentales que podemos crear a partir de estos bloques básicos de construcción presentados hoy.

¡Nos vemos pronto!