Curvas Elípticas En Profundidad (Parte 10)

---

Imagino que llegar hasta acá no debe haber sido fácil, querido lector.

Hemos pasado por nueve artículos completos de teoría de curvas elípticas, abarcando temas desde lo más básico, hasta algunas cosas realmente abstractas (los estoy estoy mirando a ustedes, divisores).

Ya es hora de que nos familiaricemos más con algunos aspectos prácticos. En particular, lo que creo que le falta a la serie es presentar algunas de las curvas reales que se usan en los algoritmos más comunes.

Al hacerlo, cubriremos algunos conceptos geniales que aún no hemos tenido la oportunidad de ver, y que cerrarán muy bien nuestro viaje.

¡Ya casi llegamos! Mantente fuerte, solo queda un sprint corto.

La Familia SECP

Nuestra historia de hoy comienza con una familia de curvas que está entre las más ampliamente desplegadas y usadas en el mundo. De hecho, ¡tu navegador muy probablemente usó una de ellas cuando se conectó a este sitio!

El nombre viene del documento donde fueron definidas, los Standards for Efficient Cryptography. Y la $p$ tiene que ver con el campo finito de orden primo sobre el cual se define la curva.

Dado que son tan omnipresentes, son un buen lugar para empezar el artículo de hoy. Hay múltiples variantes disponibles, pero solo veremos una de ellas aquí.

La Curva de Bitcoin

La curva secp256k1 es la que usan tanto Bitcoin como Ethereum.

En realidad es una curva muy simple. Su forma de Weierstrass es sencillamente:

$$y^2 = x^3 + 7$$

Sin embargo, sabemos muy bien que definir una curva elíptica no es solo cuestión de especificar su fórmula: también necesitamos definir el campo finito sobre el cual estaremos operando, y necesitamos encontrar un generador adecuado de un subgrupo cíclico grande.

Empecemos con el campo finito. Aquí está el orden (primo):

$$p = 2^{256} {-} 2^{32} {-} 2^9 {-} 2^8 {-} 2^7 {-} 2^6 {-} 2^4 {-} 1$$

Mi primera reacción al ver ese número fue "eh, eso es extrañamente específico". Es el tipo de número que te hace sospechar que algo más profundo está pasando, o al menos así es como me sentí al respecto personalmente.

Por supuesto, hay una buena razón para esta estructura particular. El número pertenece a una familia llamada los primos de Solinas (o primos de Mersenne generalizados), y su principal ventaja es que permiten la reducción modular rápida, al menos cuando se compara con algún primo random de 256 bits.

Como un bosquejo aproximado de cómo funciona esto, notemos que podemos expresar $p$ como $2^{256} {-} c$, con $c$ siendo una constante "pequeña" cuando se compara con $p$ mismo. Con esto, es fácil ver que $2^{256} \ \textrm{mod} \ p = c$.

Así que la estrategia es la siguiente: dividimos cualquier número grande que queramos reducir (digamos, 512 bits) en bits altos ($x_h$) y bits bajos ($x_l$). Podemos representar tal separación para un número arbitrario $x$ como $x = x_h.2^{256} + x_l$. Cuando aplicamos $\textrm{mod} \ p$ a la expresión, obtenemos algo fantástico: $x \ \textrm{mod} \ p = x_h.c + x_l$. Y dado que $c$ es pequeño (y también tiene una representación binaria dispersa, pero no nos preocupemos por eso ahora), ¡esta operación es súper rápida!

Campo finito, ¡listo! Ahora dirigimos nuestra atención a la estructura del grupo, empezando con su orden (número de elementos), que es este pequeño número aquí:

$$n = 2^{256} {-} 432420386565659656852420866394968145599$$

¿Qué tiene de especial eso, te preguntarás? Pues esto: es un número primo. ¿Y sabes qué significa eso? Gracias al teorema de Lagrange, estamos seguros de que todo el grupo es un solo grupo cíclico, donde cada punto que no es la identidad genera el grupo completamente.

Desde una perspectiva de seguridad, esto es ideal. La presencia de otros subgrupos más pequeños abre la puerta a algunos vectores de ataque, como el bien conocido algoritmo de Pohlig-Hellman.

Así que, en teoría, podríamos elegir cualquier punto como generador. Solo por propósitos de compatibilidad, un generador "estándar" fue seleccionado como otro parámetro de la curva.

Puedes verificar su valor aquí.

Finalmente, hay una cosita más que vale la pena mencionar sobre secp256k1 — y es sobre esa $k$ en su nombre.

Secp256k1 también pertenece a una familia de curvas llamadas curvas de Koblitz. La característica definitoria de esta familia es que tienen un endomorfismo eficientemente computable. Hay mucho material si quieres profundizar más en este tema, así que solo te daré una idea aproximada de qué se trata.

Un endomorfismo es, como ya hemos mencionado, una función que mapea $E$ (la curva) sobre sí misma. Así que lo que tenemos esencialmente es un mapa $\phi$ que actúa sobre puntos de la curva, satisfaciendo $\phi (P) = \lambda P$ para alguna constante $\lambda$.

Esto importa porque permite una multiplicación escalar más rápida usando un método llamado el método de descomposición Gallant-Lambert-Vanstone (o GLV para abreviar).

En lugar de usar la multiplicación estándar duplicar-y-sumar para encontrar $[k]P$, puedes descomponer el escalar $k$ en dos escalares más pequeños ($k_1$ y $k_2$) tal que:

$$[k]P = [k_1]P + [k_2]\phi(P)$$

Ambas multiplicaciones pueden computarse en paralelo, y luego sumarse juntas.

La aceleración es en realidad bastante significativa — aproximadamente 25–30% más rápida que la multiplicación escalar estándar. Para sistemas que realizan millones de operaciones ECDSA, esto se acumula. Sin embargo, implementar GLV correctamente es complicado y puede introducir ataques de canal lateral (side-channel attacks, como ataques de timing) si no se hace cuidadosamente.

En la práctica, muchas bibliotecas no se molestan con eso. Pero para escenarios de alto rendimiento (como nodos de blockchain validando miles de firmas por segundo), el endomorfismo GLV puede ser una optimización valiosa.

Todas estas características especiales podrían ser la razón por la que la misteriosa figura que es Satoshi Nakamoto eligió secp256k1 sobre opciones más estándar, como secp256r1. Es simple, y es rápida cuando necesitas que lo sea. Algunos también especulan que Nakamoto también evitó las curvas NIST (a.k.a. las estándar) por temor a que puedan tener puertas traseras potenciales.

Especialmente después de la controversia Dual_EC_DRBG.

Puede que nunca lo sepamos realmente. Lo que sí sabemos es que esta pequeña curva, con todos sus trucos ocultos, es responsable de asegurar cientos de miles de millones de dólares en criptomonedas. Al menos a corto plazo, ¡no se va a ningún lado!

Formas Alternativas

Hasta ahora, hemos conceptualizado y presentado curvas en su forma corta de Weierstrass:

$$y^2 = x^3 +ax + b$$

Esta es la representación "estándar". Es en lo que la mayoría de la gente piensa cuando escucha "curva elíptica". Pero esta no es la única forma que puede representar una curva elíptica, como aludimos en el primer artículo de la serie.

De hecho, mencionamos un par de formas más en ese entonces, una de las cuales quiero presentarte formalmente ahora. Aquí está la forma de Montgomery:

$$By^2 = x^3 + Ax^2 + x$$

Es diferente, pero al mismo tiempo, no es tan desconocida. Después de todo, ¡solo hay algunas pocas formas de escribir polinomios de tercer grado!

Ahora tenemos un coeficiente para $y^2$, y un nuevo término $x^2$. En general, el cambio no parece muy dramático.

Una curva que se define en esta forma es Curve25519, cuya ecuación es:

$$y^2 = x^3 + 486662x^2 + x$$

y está definida sobre el campo primo con $p = 2^{255} {-} 19$.

Muy parecido al caso de secp256k1, ese primo merece un momento de apreciación. Es un número muy simple, y también es un primo pseudo-Mersenne. Esto ayuda a hacer la aritmética modular rápida, usando técnicas similares a la reducción modular rápida presentada antes.

Sé lo que estás pensando en este punto. Frank, ¿por qué una forma diferente? ¿Qué cambia?

Las formas de Montgomery tienen una propiedad hermosa con implicaciones muy interesantes: la multiplicación escalar solo requiere usar coordenadas x. La fórmula explícita para duplicación de puntos se ve así:

$$x_{[2]P} = \frac{({x_P}^2 {-} 1)^2}{4x_P({x_P}^2 + Ax_P + 1)}$$

La suma de puntos es un poco más complicada. Aunque se puede hacer solo con coordenadas x, todo realmente encaja como un algoritmo llamado la escalera de Montgomery, que veremos en un minuto.

Antes de eso, hablemos sobre las principales ventajas de solo tener que rastrear una coordenada:

• En términos de velocidad, aproximadamente tenemos la mitad de los datos para procesar. Esto hace que la escalera de Montgomery sea aproximadamente dos veces más rápida que la multiplicación regular de Weierstrass.
• El ancho de banda también se beneficia de esta forma, porque solo necesitamos enviar las coordenadas x (32 bytes para Curve25519) en lugar de puntos completos. Esto es en realidad lo que hace el protocolo x25519 (intercambio de claves Diffie-Hellman).
• Finalmente, está el hecho de que el algoritmo de escalera de Montgomery es muy regular en su ejecución, lo que significa que el número de operaciones que realiza no depende de patrones en el escalar que se está usando para la multiplicación. Esto lo hace naturalmente resistente a un tipo de ataque llamado ataques de timing, que intentan adivinar algo sobre el escalar midiendo el tiempo que toma ejecutar un algoritmo.

Y las implementaciones de Weierstrass históricamente han tenido problemas con eso.

Suena fabuloso. ¿Entonces de qué se trata este algoritmo mágico?

La Escalera de Montgomery

En realidad, el algoritmo es hermosamente simple.

Para computar $[k]P$, necesitas mantener registro de solo dos valores: $R_0$ y $R_1$. Estos puntos satisfarán una invariante particular: $R_1 {-} R_0 = P$. Veremos por qué esto es importante en solo un minuto.

Empezando con $R_0 = \mathcal{O}$ (representado como $x = 0$ en formas de Montgomery) y $R_1 = P$, pasamos por $k$ bit por bit. Esto es, tomamos la representación binaria de $k$, y luego recorremos sus dígitos de menor significancia a mayor significancia, realizando estas actualizaciones:

• Si el bit es 0: $R_1 \leftarrow R_0 + R_1$, luego $R_0 ← 2R_0$
• Si el bit es 1: $R_0 \leftarrow R_0 + R_1$, luego $R_1 ← 2R_1$

Podemos ver un par de cosas de inmediato. Primero, la invariante efectivamente se mantiene — puedes verificar eso tú mismo con un par de ejemplos. Segundo, ambas ramas hacen exactamente una suma y una duplicación. El patrón de ejecución es idéntico, y lo que cambia es qué variable recibe cada actualización. Esta es la propiedad de tiempo constante que mencionamos antes, y la razón por la que se resisten los ataques de timing.

Finalmente, necesitamos lidiar con la suma — y aquí es donde ocurre la magia. La fórmula explícita para suma de dos puntos $U$ y $V$ es esta:

$$x_{U+V} = \frac{(x_U x_V {-} 1)^2}{(x_U {-} x_V)^2.x_{U {-} V}}$$

Algo debería llamarte la atención inmediatamente: necesitamos la coordenada x del punto $U {-} V$. Bajo circunstancias normales, esto no tendría mucho sentido — una suma que depende de otra suma (la resta es solo suma $-V$) parece un bucle imposible, y una receta para el desastre.

Pero aquí es donde entra nuestra invariante: ¡cuando sumamos $R_0$ y $R_1$, sabemos exactamente cuál es esa diferencia: $P$!

Bastante fascinante, ¿no es así?

¿Qué Pasa con el Resto?

Correcto. Ese algoritmo se ve genial y todo. Pero ¿qué pasa con toda esa cosa de ley de grupo que definimos tan cuidadosamente? O incluso peor, ¿qué pasa con toda esa teoría de divisores por la que pasamos? ¿Ya no importa eso?

No entres en pánico — ¡por supuesto que sí importa!

La forma de Montgomery es solo una forma diferente de representar curvas que también podrían escribirse en forma de Weierstrass. De hecho, hay una transformación que permite que un sistema se convierta al otro, y viceversa.

Inténtalo tú mismo: puedes convertir de forma de Montgomery a forma de Weierstrass usando el mapa $(x,y) \mapsto (x/B + A/3B, y/B)$. El otro camino es un poco más complicado, ¡pero esto debería ser suficiente para convencerte!

Dicha transformación es esencialmente un cambio de coordenadas — un mapa birracional que preserva la estructura algebraica de la curva. La ley de grupo permanece igual, los divisores permanecen iguales, y las propiedades fundamentales que hemos estudiado todas se mantienen.

Es análogo a describir el mismo objeto geométrico en coordenadas cartesianas versus coordenadas polares. El objeto mismo no cambia — solo lo estás viendo de manera diferente.

¿Así que esas intersecciones de líneas que definen la suma de puntos? Siguen ahí.

¿Los divisores? Siguen ahí.

¿La estructura del grupo? Sigue ahí.

Las formas de Montgomery simplemente permiten multiplicación escalar más eficiente. La teoría no cambia — solo la computación lo hace.

Curvas de Edwards

Curve25519 es genial para protocolos que hacen uso intensivo de multiplicación escalar, como el intercambio de claves Diffie-Hellman. Pero esto no significa que sean una bala de plata.

Por ejemplo, los algoritmos de firma digital requieren suma de puntos en lugar de multiplicación escalar. Idealmente, también necesitamos verificación rápida y tiempo de ejecución uniforme independientemente de las operaciones que se estén realizando.

En este escenario, las curvas de Montgomery se quedan cortas, ya que la suma solo tiene sentido cuando tenemos una invariante.

En cuanto a la forma de Weierstrass, el problema es que necesitamos una fórmula de suma completa — en otras palabras, una que funcione exactamente igual para todos los tipos de puntos. Debido a la existencia de un pequeño punto molesto llamado el punto en el infinito ($\mathcal{O}$), esto simplemente no es posible con la forma de Weierstrass.

Vamos a necesitar una alternativa. Y aquí es donde las formas de Edwards torcidas entran en escena.

La Forma de Edwards Torcida

Una ecuación de curva Edwards torcida se ve así:

$$ax^2 + y^2 = 1 + dx^2y^2$$

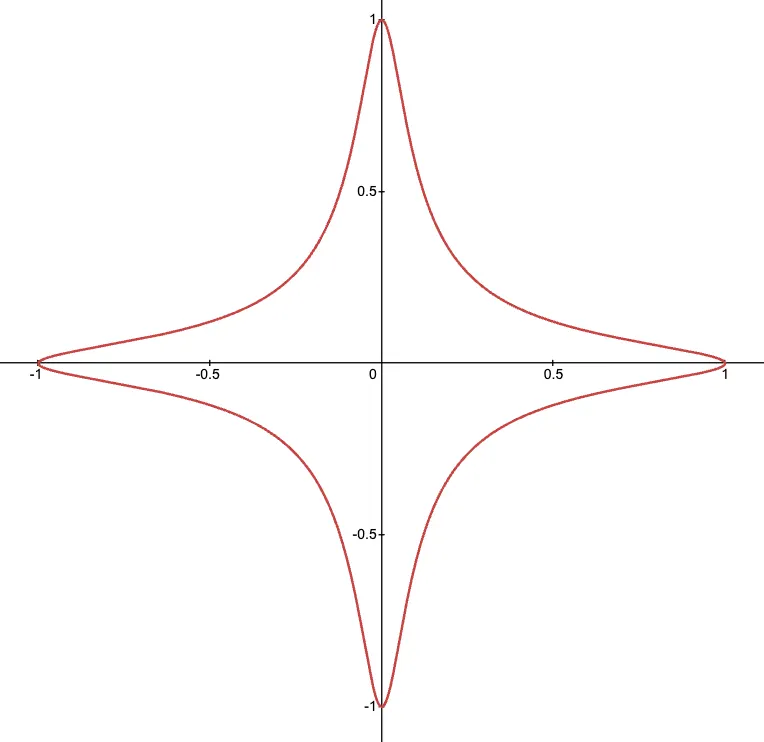
Antes de que surjan confusiones, debo aclarar: torcida aquí no tiene nada que ver con twists de curvas, como los que discutimos previamente en la serie. Es solo una elección de nomenclatura desafortunada.

Edwards Torcida es simplemente el nombre de esta forma de curva, distinguiéndola de las curvas Edwards originales propuestas por Harold Edwards en 2007 (que tenían $a = 1$). Lo "torcido" solo significa que hemos agregado el parámetro $a$ para generalizar la forma original.

Con eso fuera del camino, podemos enfocarnos en las cosas que esta forma tiene para ofrecer.

La característica a destacar de las curvas Edwards torcidas es, como se insinuó previamente, su fórmula de suma completa. En forma Edwards torcida, la suma de puntos está dada por:

$$(x_1, y_1) + (x_2, y_2) = \left(\frac{x_1y_2 + y_1x_2}{1 + dx_1x_2y_1y_2}, \frac{y_1y_2 {-} ax_1x_2}{1 {-} dx_1x_2y_1y_2}\right)$$

Echa un vistazo cercano a esta fórmula. ¿Notas algo interesante?

A primera vista, tal vez no. Pero ¿qué tal si te dijera que intentes sumar $P$ a sí mismo? La fórmula parece mantenerse bien. ¿Y qué tal la identidad? En este sistema de coordenadas, la identidad es el punto $(0,1)$ — puedes verificar por ti mismo —, y la fórmula anterior también funciona.

Ese es exactamente el poder de la suma en curvas Edwards torcidas: no hay casos especiales. ¡La fórmula es completa en el sentido de que simplemente funciona para todas las entradas!

Contrastemos esto con la forma de Weierstrass, donde tenemos que manejar varios casos diferentes:

• Si $P = \mathcal{O}$, entonces $P + Q = Q$
• Si $Q = \mathcal{O}$, entonces $P + Q = P$
• Si $P = -Q$, entonces $P + Q = \mathcal{O}$
• Si $P = Q$, usar la línea tangente (duplicación de puntos)
• De lo contrario, usar la línea a través de $P$ y $Q$

Esos son cinco casos diferentes que necesitan ser verificados y manejados por separado, y dos de esos requieren fórmulas diferentes.

Tener una sola fórmula completa tiene algunas ventajas:

• La más obvia es su simplicidad. Menos ramas significa menos oportunidades para errores. Cuando se trata de código criptográfico donde un solo error puede ser una catástrofe, esta simplicidad no es menos que invaluable.
• Segundo, dado que siempre ejecutamos la misma operación, obtenemos ejecución de tiempo constante. Muy parecido a las curvas de Montgomery, esto proporciona resistencia contra ataques de timing.
• Por último, la fórmula es simétrica y eficiente para ambos operandos. Para verificación de firmas especialmente, donde estás computando combinaciones lineales de puntos (algo como $[s]G + [h]P$), tener sumas rápidas y uniformes hace una diferencia real.

El intercambio cuando se compara con curvas de Montgomery es lo que esperarías: la multiplicación escalar no es tan rápida. Pero eso está completamente bien — y qué curva elegimos depende en gran medida del tipo de protocolos para los que las usaremos.

Ed25519

Una de las curvas Edwards torcidas más ampliamente usadas es Ed25519, que tiene la forma:

$$-x^2 + y^2 = 1 {-} (121665/121666)x^2y^2$$

¡Cuidado! ¡Esa división ahí es módulo p!

La curva está definida sobre $p = 2^{255} {-} 19$. Y ese es un valor familiar — es el mismo que usamos en Curve25519.

Esto no es coincidencia. De hecho, Ed25519 y Curve25519 son biracionalmente equivalentes — son la misma curva algebraica subyacente, pero representada en diferentes sistemas de coordenadas.

¡Como la relación que ya vimos entre las formas de Montgomery y Weierstrass!

Porque podemos esencialmente usar la misma curva en ambas formas, podemos optimizar para nuestro caso de uso y aún preservar las garantías de seguridad ofrecidas por la curva. Incluso es posible transformar puntos entre formas, en casos raros donde necesitamos tanto suma rápida como multiplicación escalar rápida.

¡Y creo que eso es increíble!

Curvas Amigables para Emparejamientos

Para cerrar, hablemos brevemente sobre curvas diseñadas específicamente para emparejamientos.

¡Si no has leído los artículos anteriores sobre emparejamientos en esta serie, sugiero fuertemente hacerlo antes de saltar a esta siguiente sección!

Al diseñar este tipo de curva, hay algunos requisitos extra que necesitamos tomar en cuenta, como:

• Necesitamos un subgrupo de orden primo de tamaño $r$.
• Necesitamos tener un grado de inmersión $k$ tal que $r$ divida $q^k {-} 1$, donde $k$ es suficientemente pequeño para eficiencia pero suficientemente grande para seguridad.
• Y algunas otras condiciones que no hemos discutido en absoluto, como garantizar seguridad de twist.

Encontrar curvas que satisfagan estas condiciones no es una tarea fácil. Por ejemplo, si eliges alguna curva aleatoria, las probabilidades son que el grado de inmersión sea muy grande — cercano al orden del grupo, en realidad — lo que hace que los emparejamientos en esas curvas sean completamente imprácticos.

Para hacer este punto absolutamente claro, recuerda que estamos realizando operaciones en extensiones de campo. El grado de inmersión nos dice cuántos elementos del campo base necesitamos almacenar para representar un solo elemento en la extensión. Y a medida que $k$ crece, las operaciones se vuelven exponencialmente más costosas, hasta el punto de ser absolutamente imposibles de manejar.

Entonces, ¿cómo procedemos a encontrar estas curvas esquivas?

Método de Multiplicación Compleja

La técnica principal para construir curvas amigables para emparejamientos se llama el método de Multiplicación Compleja (CM).

En lugar de generar curvas aleatorias y rezar para que tengan las propiedades correctas, el método CM trabaja hacia atrás: especificamos las propiedades que queremos (grado de inmersión, nivel de seguridad, etc.) y resolvemos un cierto problema para encontrar parámetros de curva que logren esos objetivos.

Dicho problema viene de un área que no hemos explorado realmente en profundidad, aunque sí mencionamos un par de cosas al respecto: el estudio de endomorfismos en curvas elípticas.

Algunas curvas tienen más endomorfismos disponibles que solo la multiplicación escalar estándar, y el endomorfismo de Frobenius (y sus potencias). Cuando esto sucede, se dice que la curva está equipada con multiplicación compleja.

¡Se llama así porque podríamos encontrar un endomorfismo que satisfaga una condición como $\psi ^2 + D = 0$ (en el anillo de endomorfismos). Esto es análogo al número complejo $i$ satisfaciendo $i^2 + 1 = 0$, ¡de ahí la nomenclatura!

Esto solo sucede si las curvas satisfacen una relación especial (la ecuación CM), dada por:

$$4q = t^2 {-} Dy^2$$

Donde $q$ es el tamaño del campo, y $t$ es la traza de Frobenius — que simplemente se define como esta diferencia:

$$t = q + 1 {-} \#E(\mathbb{F}_q)$$

Tener una restricción extra es en realidad beneficioso en este caso: significa que podemos buscar sistemáticamente curvas con las propiedades que necesitamos.

El procedimiento aproximadamente va así:

1. Elige tu grado de inmersión objetivo $k$.
2. Elige un discriminante pequeño $D$. Los valores $D$ más pequeños son más fáciles de trabajar, y típicamente toman valores como $D = 1, 2, 3, 7, 11$, etc.
3. Resuelve la ecuación CM para diferentes valores de $y$, obteniendo pares $(q, t)$.
4. Verifica si $q + 1 {-} t$ tiene un factor primo grande $r$. Esto garantizará la existencia de un subgrupo de orden $r$.
5. Verifica que $r$ divida $q^k {-} 1$. Esto asegura que el grado de inmersión es exactamente $k$ (o un divisor de $k$).
6. Verifica que $q$ sea primo (o una potencia prima). Recuerda que $q$ define nuestro campo.

Si logramos cumplir todas estas condiciones, ¡entonces habremos tropezado con una curva amigable para emparejamientos! Fácil, ¿verdad?

Nota que la ecuación de la curva misma (los valores $a$ y $b$ en $y^2 = x^3 + ax + b$) puede entonces elegirse algo libremente, siempre y cuando la curva tenga el número correcto de puntos (para obtener la traza de Frobenius requerida).

Esto es realmente solo la punta del iceberg en este tema. No entraremos en más detalle, ya que es una madriguera de conejo muy profunda que lleva a teoría algebraica de números y teoría de campos de clases.

Me encantaría decir "y eso está muy por encima de mi sueldo", pero hago esto gratis, así que...

También, necesitamos saber cómo contar puntos en una curva — otro esfuerzo interesante que dejo a tu curiosidad.

Y además de eso, estamos interesados en otras propiedades, como seguridad de twist, aritmética eficiente, y evitar ciertos vectores de ataque. En resumen:

Encontrar curvas amigables para emparejamientos es realmente difícil

Por esta razón, los criptógrafos han optado por definir algunas familias paramétricas en lugar de resolver el problema CM cada vez. Estas son fórmulas que generan curvas adecuadas para cualquier nivel de seguridad requerido — una especie de atajo curado, si quieres. Algunas de las más importantes incluyen:

• Barreto-Naehrig (BN): $k = 12$, altamente eficiente.
• Barreto-Lynn-Scott (BLS): $k = 12$, $24$, o $48$, y mejor seguridad que BN.
• Kachisa-Schaefer-Scott (KSS): $k = 18$, término medio entre eficiencia y seguridad.

Que son los métodos usados para derivar algunas de las curvas amigables para emparejamientos más ampliamente usadas, entre las cuales podemos encontrar BLS12–381 y BN254.

Al momento de escribir esto, BLS12–381 es el estándar de oro actual para criptografía basada en emparejamientos. Viene de la familia BLS con $k = 12$, definida sobre un campo primo de 381 bits. La ecuación de la curva es realmente simple:

$$y^2 = x^3 + 4$$

Es usada por gigantes como Ethereum 2.0, Zcash, Filecoin, y también se usa en la mayoría de sistemas modernos de pruebas de conocimiento cero.

Resumen

Así que sí — aunque hemos pasado por mucha teoría, quiero que nos detengamos por un momento y apreciemos cuánto más hay aún por descubrir.

De hecho, la mayoría de las cosas que definimos para curvas elípticas pueden generalizarse al estudio de variedades algebraicas.

En resumen, las curvas elípticas son estructuras hermosas que ocultan un nivel asombroso de complejidad detrás de una fachada aparentemente inofensiva.

Reúnen diferentes áreas de las matemáticas con gracia increíble, y logran un balance fantástico entre eficiencia computacional y seguridad.

Debido a la amenaza de las computadoras cuánticas, se cree que la criptografía de curvas elípticas será obsoleta pronto, y será reemplazada por la oleada actual de algoritmos post-cuánticos que se están probando y desarrollando. A corto plazo, sin embargo, ECC no es probable que vaya a ningún lado, y probablemente de la misma manera que aún vemos RSA siendo usado hoy, estoy dispuesto a apostar que va a quedarse por un buen rato.

¡Eso va a ser todo para esta serie!

No me considero un experto en el tema. De hecho, probablemente he aprendido tanto como tú en la elaboración de estos artículos, ya que cada uno de ellos ha tomado mucho esfuerzo de investigación, especialmente en esos momentos cuando sentía que las ideas no estaban haciendo clic completamente en mi cabeza.

Mi esperanza es que hayas encontrado este material útil, y tal vez incluso divertido y atractivo. Y si encuentras el tema interesante, me gustaría alentarte a no parar aquí — hay libros fantásticos con una cobertura mucho, mucho más profunda de curvas elípticas por ahí.

¡Y si algo, ya sabes dónde encontrarme!

¡Salud!