Elliptic Curves In-Depth (Part 6)

Last time around, we learned to speak the language of divisors. This is hugely important to gain a deeper understanding of elliptic curves, and is crucial to understand pairings — a construction we’ll tackle in the next couple articles.

Before that though, I want to take the time to really submerge ourselves into the theory, and explore a few things that we usually take for granted during our analysis, but are in fact not evident at all.

I promise — this will be the final stretch of bizarre theory (before we get to pairings, at least!).

That being said, this article is perhaps less practical than the others, and more focused on pure theory. Still, the ability to count points in elliptic curves is super important, but we’ll not be questioning why today.

Without further ado, let’s go!

Rational Points

One of the fundamental assumptions when working with elliptic curves over finite fields, is that there exist points on the curve with integer coordinates.

Points like $(1,1)$, $(2,3)$, or $(5,8)$.

Think about this for a second. Does this seem evident? Can we always find these integer-valued points?

More generally, we could try to find rational points: points whose coordinates are rational numbers. Depending on the curve, determining whether the curve has rational points or not can be very easy, or extremely complex.

In fact, finding rational points on curves is a classic example of Diophantine equations — polynomial equations where the goal is to find integer or rational solutions.

Fermat’s Last Theorem, which took over 350 years to prove, is perhaps the most famous example.

Guess into which of the two categories elliptic curves fall...

Yeah, of course it falls into the latter.

To get a good grasp on the ideas behind finding rational points, let’s first focus on a familiar curve, where it happens to be really easy to find rational points: a circle.

Rational Points on the Circle

Circles are represented by this simple equation:

$$x^2 + y^2 = R^2$$

Where $R$ is the radius. How would we go about finding rational points on this curve?

Let’s begin by trying to find at least one. It just so happens that all the points where the circle intersects the axes are rational: $(1,0)$, $(0,1)$, $(-1,0)$, and $(0,-1)$.

Great start! Now, we’ll use these points as seeds. Take the point $(0,1)$, for example. Then, draw a line going through it, that has a rational slope $m$, which we can write as $m_1 \ / \ m_2$. If you work out the resulting line equation, you’ll get:

$$y = \frac{m_1}{m_2}x + 1$$

This line will intersect the circle at another point:

Click to zoom

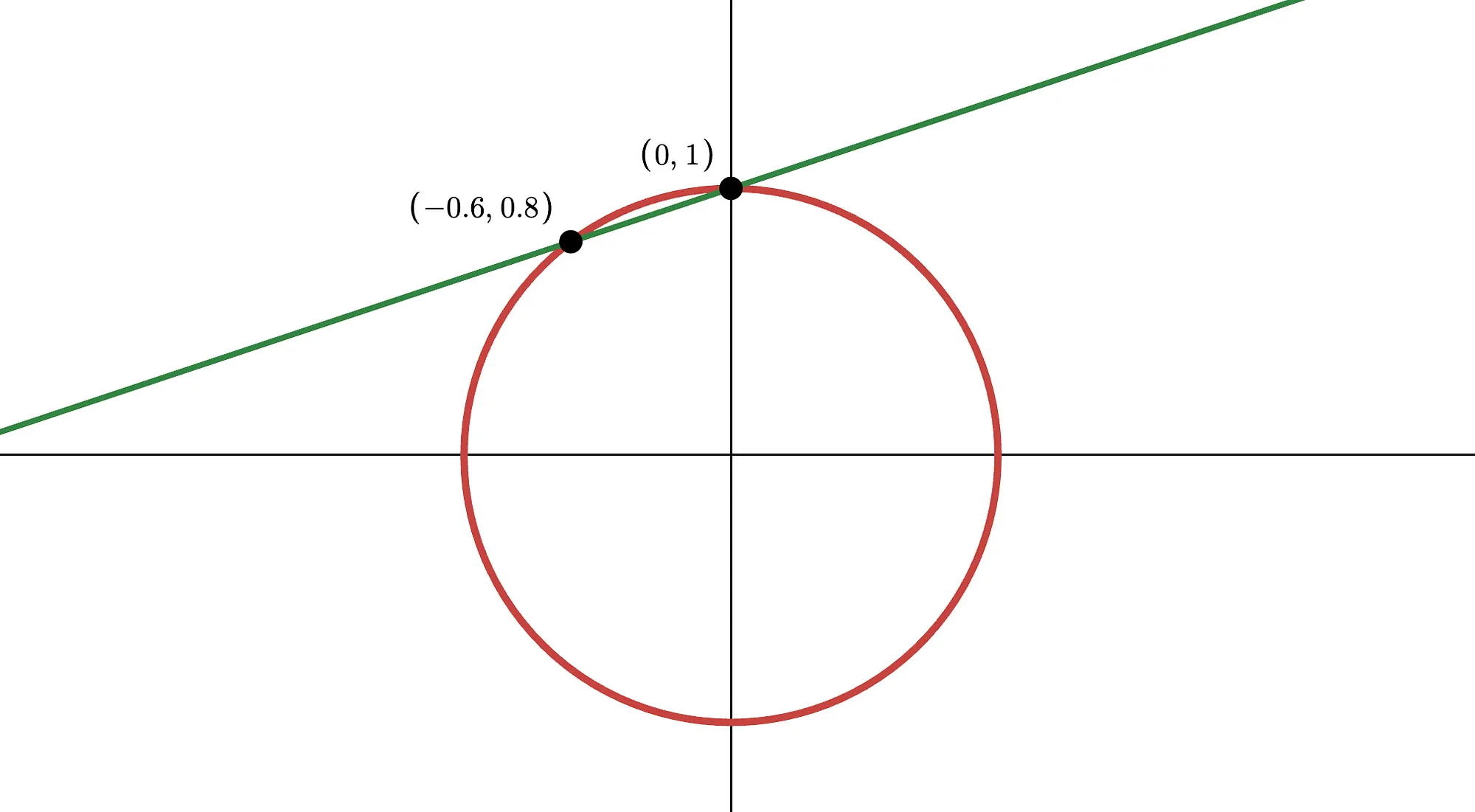
You can try this yourself in Desmos.

Oh, what’s that? The new point is rational!

Was that a fluke?

No, it wasn’t. However, justifying this takes some work.

Galois Conjugates

We first need to define what a rational function is: it’s a function that can be expressed as the ratio of two polynomials with rational coefficients. Our line is clearly a rational function — after all, it’s a polynomial with rational coefficients in itself!

When we work with these rational functions, the intersection points between curves and our rational function satisfy a special condition.

A condition that we can only understand, if we know what a Galois group is.

For this, I suggest a quick refresher on what the algebraic closure of a field is.

A Galois group is a group whose elements are functions — automorphisms, to be precise. Just a fancy name to call bijective functions which take an element of a set, and map it to another element of the same set. They “shuffle things around”, so to speak.

But not any automorphism set — it’s the set of all such automorphisms that fix elements in the base field $K$ (meaning that they act like the identity), while they shuffle around elements in the the algebraic closure $\bar{K}$. Like this:

Click to zoom

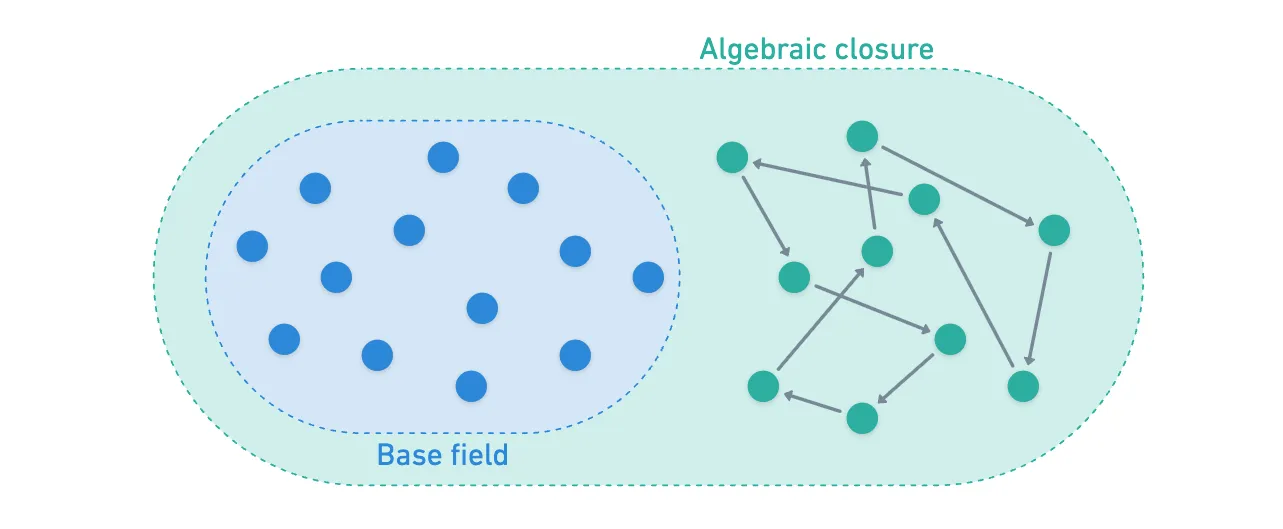
And we denote the group $\textrm{Gal}(\bar{K}/K)$.

This is the point where I presume you’re asking yourself “but Frank, why the heck should I care about this?”.

Here’s the deal: we can show that the points of intersection between a curve and a rational function need to come in Galois conjugates of the Galois group $\textrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$ — where $\mathbb{Q}$ are the rational numbers. This means that all the points are either elements of the base field, or all belong in the algebraic closure (but not to the base field).

Or in plain english: either they are all rational points, or they are all irrational. No middle ground!

Actually, this is not strictly correct, but the simplification will have to do for today.

The more precise definition of a Galois conjugate is that the set of intersection points are invariant under the action of the group, which ends up kinda meaning what we just said.

Showing this is quite involved. You can find more information in textbooks like this one, but for our intents and purposes, I think we can just run with simple the conclusion. And also, here’s a fun video about Galois theory and some of its other applications:

Alright, let’s land back onto reality. I’ll repeat the conclusion of this mathematical sidetrack:

Either all intersection points of a rational function and a curve are rational, or they are all irrational.

Naturally, in our circle example, since we started with a rational point and drew a rational function (line) through it, the other intersection point was guaranteed to be rational. And the fun thing is that we can keep repeating this process infinitely many times.

In a process that’s very akin to stereographic projection. By the way, it seems like a simple method, but it took a mathematical genius like Henri Poincaré to actually propose it. So there’s that.

But you know what? This doesn’t work with any circle. Suppose we choose $R = \sqrt{2}$ instead. Then, try to find a rational point to start drawing lines through. You’ll quickly find that you can’t find one. And indeed, this circle has no rational points at all.

We can prove this more rigorously, but again, I’m already asking you to believe me on a couple things—so what’s just another leap of faith at this point?

That’s enough circles for today, though. What does this all have to do with elliptic curves?

Rational Points on Elliptic Curves

The line drawing technique we highlighted earlier should not be unfamiliar to us at this point. It’s essentially what you do during point addition and doubling when working with elliptic curves — which results in the Mordell-Weil group we’ve already talked about.

Although, when we talked about it, we didn’t question whether if rational points existed or not, and neither did we ask ourselves the size of these groups — or more importantly, whether they were finite or infinite.

And we must be able to find rational points, because the whole gist of elliptic curves in cryptography is to work with them over finite fields!

To illustrate the challenges, let’s again use some examples.

Consider the curve $y^2 = x^3 - 2x + 1$. This curve has a few rational points you can spot at a glance — for example, $P = (0,1)$. Now, we cannot draw just about any line, like we did with the circle. We need to follow the chord and tangent rule.

So let’s start by doubling $P4. We need to find the line tangent to the curve at said point. The slope for said line is a result we explored a couple articles back — and it just so happens to be a rational number.

Therefore, the tangent line is a rational function. Since $P$ is rational, we know the other intersection point will be rational as well. Like clockwork, $[2]P$ lands at $(1,0)$.

Click to zoom

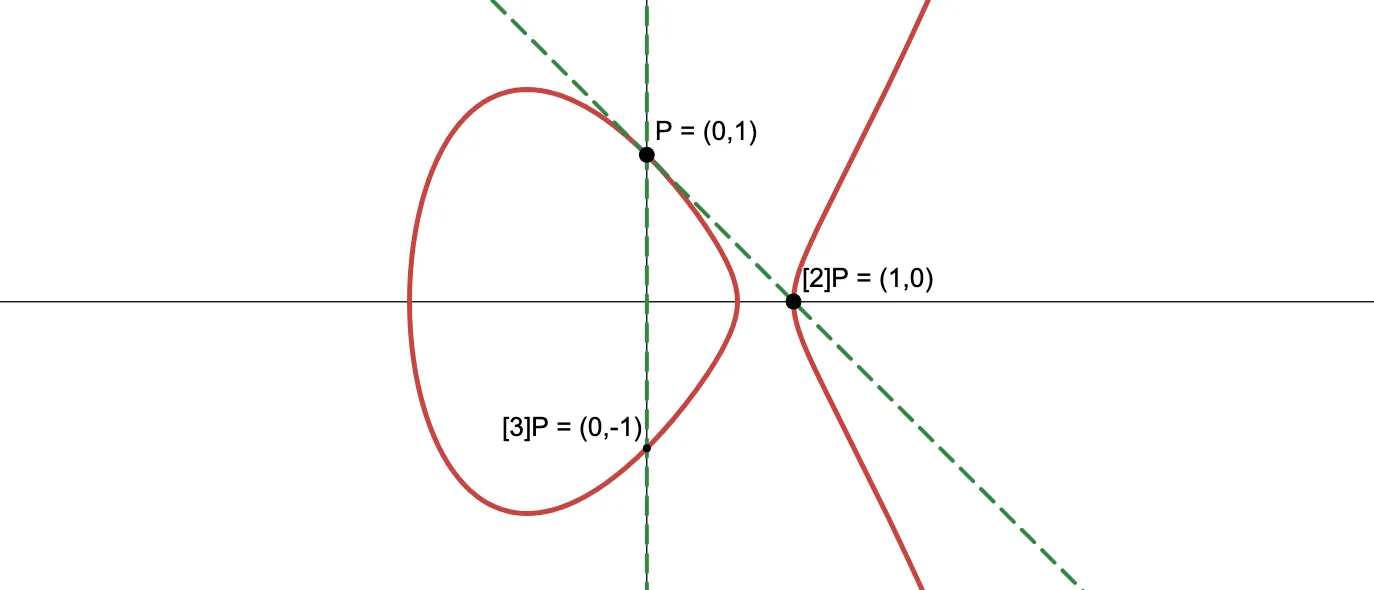
Adding $P$ and $[2]P$ yields $[3]P = (0,-1)$. And finally, $[4]P = \mathcal{O}$. This is a 4-point finite cyclic group, since $[5]P = P$.

Let’s try with a different curve now: $y^2 = x^3 - x + 1$. One trivial rational point is $P = (1,1)$, so let’s again draw the tangent, and see what happens.

Feel free to try this yourself again in Desmos. At least until you get tired. Spoiler: you won’t find any cycles!

Did you try it? If you did, you probably noticed that new and weird points seemed to keep popping up, never repeating a single one — all of them being rational points. You could keep doing this forever, and never find a duplicate.

What we found just stumbled upon is an infinite group of rational points.

Question time: are those all the rational points in the curve?

Believe it or not, this question has kept many mathematicians up at night for quite a long time. And we still don’t know how to answer that.

We have clues, though. And a famous conjecture, that’s hasn’t been proven yet, but if true, would give us tools to answer this question.

Rank

To understand the conjecture, we first need to introduce what the rank of a curve is.

In the previous examples, there were some generator elements (the P points we used) that produced finite groups, while other produced infinite groups. Likewise, we say that $P$ has a finite order in the former case, or an infinite order in the latter.

Now, finite groups are easy to describe — we can simply list all their elements. But for infinite groups, much like for infinite sets, this is not possible.

So what we do is describe them in terms of their generators.

We can use the concept of a group presentation for this, for shorthand notation.

This new idea allows us to reformulate the question we posed a few paragraphs ago — we now ask:

How many different infinite-order generators do we need to generate all the points of infinite order in an elliptic curve?

That number, my friends, is called the rank of a curve.

You can think of it like the number of “dimensions” of an elliptic curve group.

In fact, there’s a theorem (the Mordell-Weil theorem) that states that we can express the number of rational points on an elliptic curve as:

$$E(\mathbb{Q}) \simeq E(\mathbb{Q})_{\textrm{tors}} \oplus \mathbb{Z}^r$$

Which translated to human dialect, means that it can be expressed as the combination of a finite subset (the torsion group, which we’ll discuss in the next article), and another group that’s isomorphic to $\mathbb{Z}^r$ — that little $r$ being the rank of the curve.

It looks like we’re making progress, but unfortunately, we’re not. Because now the question becomes:

How do we determine the rank of an elliptic curve?

How do we even begin trying to answer that?

And this is where it gets really complicated. Grab onto your seat — things are about to get mathematically turbulent.

The Conjecture

Ok, first, a little history.

Around the year 1965, the English mathematicians Bryan John Birch and Peter Swinnerton-Dyer were studying this same problem that’s occupying our minds at present.

Their approach was simple. They took a finite field (of prime order $p$), and then they counted how many of the possible $x$ and $y$ combinations were solutions to some elliptic curve$$E. And they dubbed the number $N_p$.

Yeah, not the type of rigorous approach we’d have imagined, perhaps.

And for a single curve, they tried with various different $p$ values. And then, they plotted this function:

$$f(x) = \prod_{p \leq x} \frac{N_p}{p}$$

I must admit, this seems rather... Random. But in an unexpected turn of events, they stumbled upon this plot, which has since become quite famous:

Click to zoom

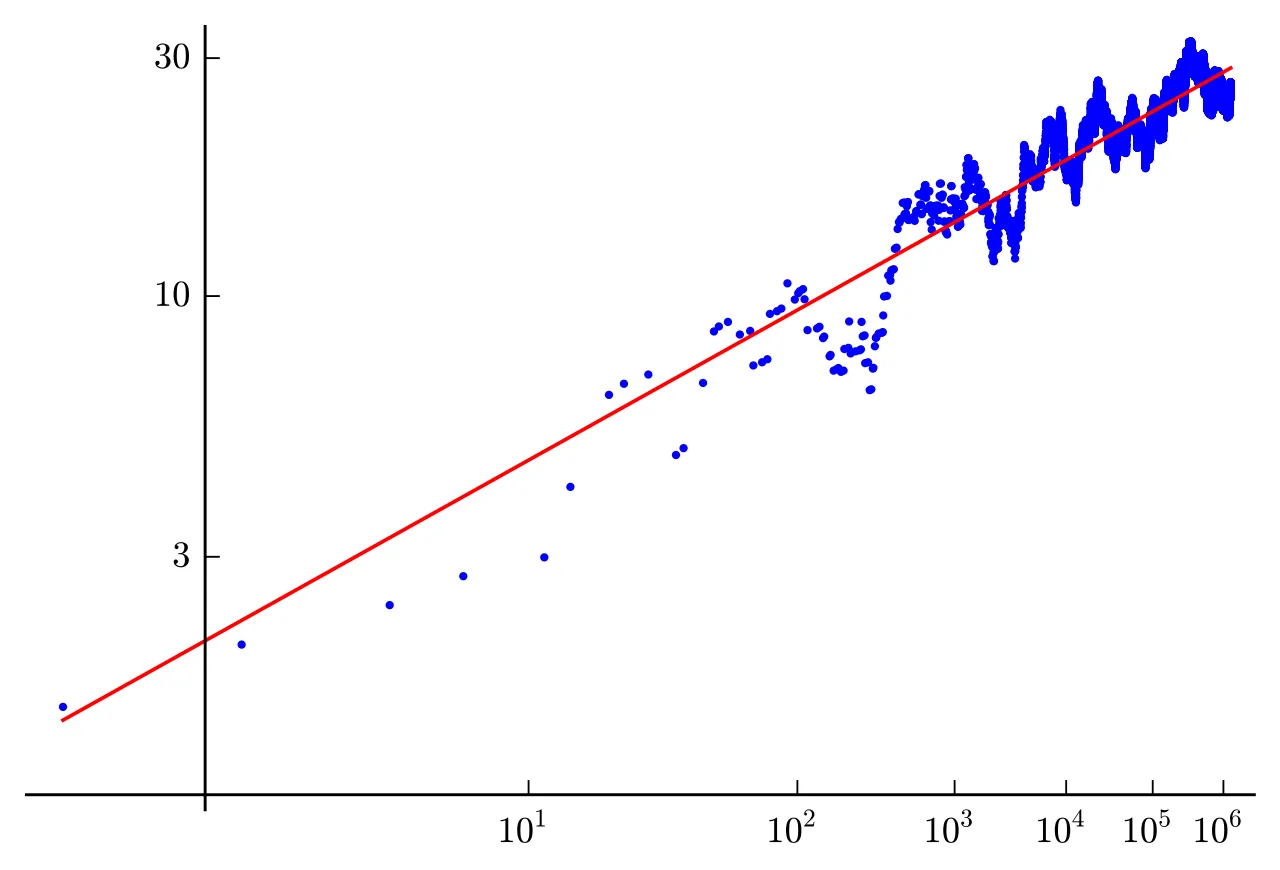
That red line you see corresponds to the function:

$$g(x) = C.\textrm{log}(x)^r$$

And yes, that $r$ exponent is the rank of the curve!

Paradoxically, other curves of known rank seemed to follow this trend — which led to the question: does this happen for every elliptic curve?

This became known as the Birch and Swinnerton-Dyer conjecture (or BSD conjecture for short), and it’s one of Millennium Problems proposed by the Clay Mathematics Institute that remains unsolved.

You can win 1 million dollars if you solve it!

It’s a conjecture that, if true, would allow us to know the rank of elliptic curves with total certainty. However, the form in which I showed you the problem is rather inconvenient, because of the whole solution counting stuff.

Can’t we find another more convenient way to formulate the problem?

L-functions

L-what?

To transform the conjecture into something that’s more manageable, we have to submerge ourselves into the perplexing and almost mystical world of complex analysis.

L-functions are complex-valued functions that are well known for having this strange ability to connect seemingly disconnected areas of maths. For instance, the Riemann hypothesis — a problem that, if solved, would entirely reveal the structure of the elusive prime numbers — is formulated in terms of an L-function.

The key insight is that they provide a way to analytically study arithmetic objects. It’s a mouthful, I know.

At some point, mathematicians realized that the conjecture could be reformulated into a more elegant form, by using these L-functions. I’m really not an expert in this field, so I’ll just give you the definition, and the small insights I was able to catch.

The Refined Conjecture

Okay, let’s define a couple things.

For each prime number $p$, we first define a number $a_p$ as:

$$a_p = p - N_p$$

Then, we use it to define what’s called a local factor:

$$L_{(p)}(E,s) = \frac{1}{1 - a_pp^{-s} + p^{1 - 2s}}$$

Where $s$ is a complex-valued variable.

You can see that $E$ is also an input to the function, as it impacts the value $N_p$, which depends on $E$.

Finally, we take the product of the local factors over the entirety of the prime numbers:

$$L(E,s) = \prod_p L_{(p)}(E,s) = \prod_p \frac{1}{1 - a_pp^{-s} + p^{1 - 2s}}$$

This is known as the Hasse-Weil L-function.

With this, the Birch-Swinnerton Dyer conjecture can be reformulated as:

The rank of an elliptic curve $E$ equals the order of vanishing of $L(E,s)$ at $s = 1$.

Let’s try to break that down just a little.

When we say order of vanishing, we’re actually talking about how many times you need to take derivatives of the function before you get a non-zero value. For example:

• If $L(E,1) \neq 0$, the order of vanishing is $0$, and the rank is $0$.
• If $L(E,1) = 0$, but $L’(E,1) \neq 0$, the order of vanishing is $1$, and the rank is $1$.
• If $L(E,1) = 0$ and $L’(E,1) = 0$, but $L’’(E,1) \neq 0$, the order of vanishing is $2$, and the rank is $2$.

And so on.

What’s quite magical is how this encodes the rank in the derivatives. There’s probably a good explanation for this, but for now, it honestly goes beyond my current understanding of the subject.

L-functions in general seem to have the ability to encode information for algebraic objects — values we call invariants.

Just like the j-invariant we discussed a few articles back.

In fact, the BSD conjecture is a special case of a more modern and more far-reaching conjecture called the Bloch-Kato conjecture, which is an attempt at explaining why these L-functions have such a remarkable behavior.

It’s a very cryptic, mysterious, and fascinating area of research.

Summary

I think that’s more than enough for today.

You’ll probably leave this article with more questions than answers. In a way, that’s the beauty of mathematics: we still have many problems to solve, and a lot of mysteries to uncover.

This also highlights how complex elliptic curves are. And remember — it all starts with a very innocent-looking expression:

$$E: y^2 = x^3 + ax + b$$

I hope that, at the very least, I could convince you that rational points in elliptic curves do exist, and we can use them as a foundation to build some cool cryptography on.

Our goal lead us down a path of mathematical weirdness. There’s always more to know, and I think it’s very important to go as far into a topic as one finds practical, or fun. It’s often better to focus on the bigger picture first, and to refine the details later.

That’s what works for me, anyway!

Well then! In the next article, we’ll continue with more crazy definitions, but with a more clear focus: understanding pairings.

See you soon!