Cryptography 101: Threshold Signatures

This is part of a larger series of articles about cryptography. If this is the first article you come across, I strongly recommend starting from the beginning of the series.

In the previous article, we learned about polynomials and saw a couple of their applications.

However, this new piece of cryptography is seemingly disjoint from everything we've learned so far. Nevertheless, there are cool ways to combine them with previous concepts, such as digital signatures.

This article will be solely dedicated to explaining one such example, where we'll combine the usual signing techniques with polynomials, to create an interesting hybrid scheme. We'll be working in the context of elliptic curves, and use $G$ and $H$ to denote group generators for a group $\mathbb{G}$.

I'll be loosely basing my explanation on this paper, with some adjustments in the hopes of making things easier to navigate.

Still, a friendly disclaimer: threshold signatures are not simple to explain. There are a lot of nuances that we'll need to clarify. So let's first look at a brief summary of what they are and what they do, before really diving into the mathematics behind them.

Just Enough Signers

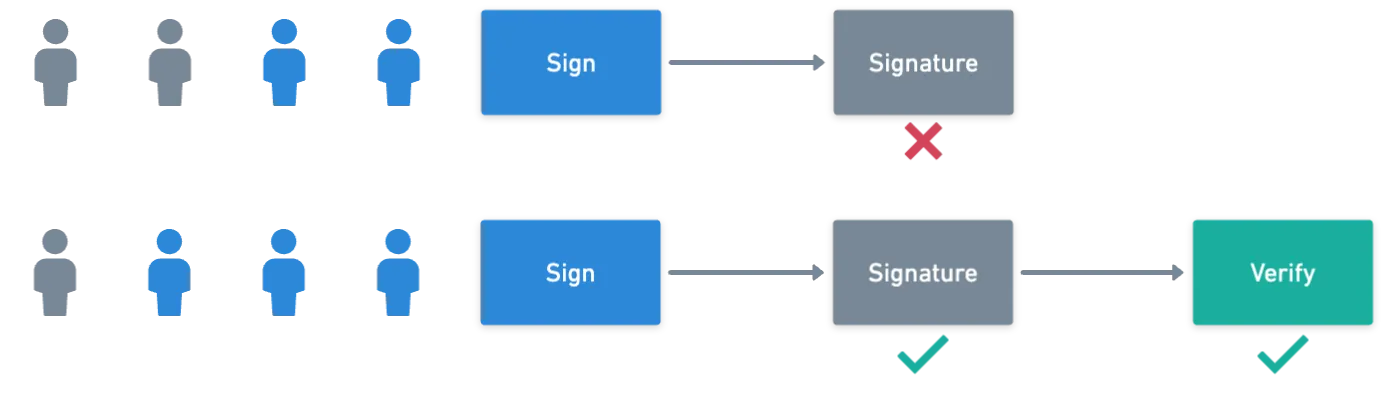
Threshold signatures are a type of multisignature — meaning that multiple participants are required to sign a message. But this time, it's not necessary for every participant to do so.

Imagine a group of ten people who have admin privileges for an application. To perform some sensitive action, we require at least three approvals.

This way, we don't have to bother all of the admins at the same time; just a subset of available signers will be enough.

This feels like an upgrade to the multisignature scheme we explored previously, where all signers were required to participate. But in reality, achieving this result involves flexing some more cryptographic muscles.

Click to zoom

We can divide threshold signatures into three major steps or algorithms (just like most signature schemes):

• Key generation (KeyGen), which is an algorithm that outputs a shared private and public key pair,
• Signing, where a message is processed along with the private key and a nonce to obtain a pair $(r, s)$,
• And verification, the step where the signature is validated against the message, and the public key.

When working with threshold signature schemes, the key generation and signing steps, which were rather straightforward in past examples, will be replaced by more complex processes involving communications between the signers. Luckily, verification remains the same — so our focus will lie on the first two steps.

Notice that the idea of requiring a threshold of signers is very reminiscent of the minimum amount of points to reconstruct a polynomial via interpolation. And in fact, this is at the core of how threshold signatures work.

Also, in order to keep things clear, we must say that the signers or participants are ordered. Each one will have an identifier or index, ranging from $1$ to $n$, the total number of participants.

Our goals are set, and the introduction is over. Shall we get to the good stuff?

Preliminaries

In threshold protocols, sharing information is key. Ultimately, the ability of a set of signers to share information is what will enable them to produce signatures.

We've already seen that sharing a secret can be achieved with Shamir's Secret Sharing (SSS). The idea was to evaluate a polynomial at many different values, and to share the results as points. And with those points, we could interpolate back the original polynomial.

But there's a catch. How can any receiver check whether if the values they receive are correctly calculated? Or, in other words, is there a way to prove that the points are effectively related to the original polynomial?

And you may be wondering why would the values be incorrect? Why would anyone send a wrong value? There are at least two reasons to consider: errors in communication, and malicious activity. It's possible that an attacker could be trying to break our signature model — we can't necessarily expect everyone to behave correctly, and we must take action to mitigate this possible scenario.

To address this concern, we'll require a new tool.

Verifiable Random Secret Sharing

What we do is ask the sharer to make a commitment. This will bind the sharer to their secret information (their polynomial), so that later they just can't produce invalid values.

This idea is what's behind Verifiable Random Secret Sharing (VRSS), sort of a drop-in replacement for SSS. What we want to do is commit to the coefficients of our polynomial — and for this, we'll require not one, but two of them:

$$f_i(x) = a_{i,0} + a_{i,1}x + a_{i,2}x^2 + ... + a_{i,t}x^t$$ $$f_i'(x) = b_{i,0} + b_{i,1}x + b_{i,2}x^2 + ... + b_{i,t}x^t$$

Why, you ask? Because commitments need to be hiding. We don't want to reveal the coefficients, so their commitments should be blinded. The coefficients of the second polynomial are in fact these blinding factors!

So by using our group generators, each participant $i$ calculates and broadcasts the commitment values $C_i$, one for each of the coefficients in the polynomials:

$$C_{i,m} = [a_{i,m}]G + [b_{i,m}]H$$

Cool! Now all that remains is sharing. And for this, everyone will need to evaluate their polynomial. Since every participant has an index $j$, we can make the choice of evaluating the share for a target player at their index, so $f_i(j)$.

What this means is that individuals will get $f_i(j)$ and $f_i'(j)$ from some other participant $i$.

And upon receiving these values, participant $j$ can validate them as follows:

$$[f_i(j)]G + [f_i'(j)]H = \sum_{m=1}^{t-1} [(j)^m]C_{i,m}$$

That's just about it! We now have a mechanism to share secret information, in a way that's verifiable. With this tool, we can start building our signature scheme.

Key Generation

Since there are multiple parties involved in threshold signatures, each participant will hold an integer $d_i$ as their share (or piece) of a private key.

However, this is not a randomly chosen integer, as per usual. Instead, the participants engage in a process where they interact with each other, ultimately producing their share of the private key. These kind of protocols are called Distributed Key Generation (DKG) algorithms.

And we can use VRSS to build our algorithm. How convenient!

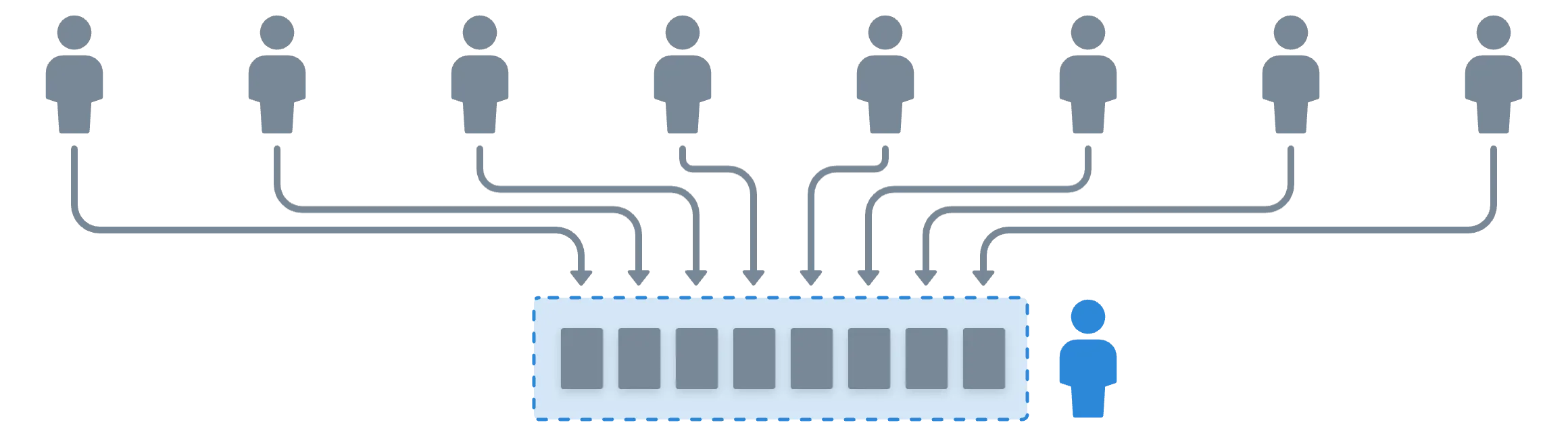
The idea is that each participant will receive a share from each of their peers, and they will use these verified values to calculate their private key share:

$$d_i = \sum_{j=1}^m f_j(i)$$

It's possible that some values do not pass verification; some parties may be disqualified in this case. This is why VRSS is important.

Still, we'll go with the happy path to keep things relatively simple.

The output of the DKG is a piece of a shared private key, $d$. None of the parties involved in this protocol know this value — only its pieces.

Click to zoom

Finally, we need a public key. And for this, each participant broadcasts their secret independent or zeroth coefficient, $a_{i,0}$. This secret cannot be disclosed as such, and therefore, it is transmitted as a public key share:

$$Q_i = [a_{i,0}]G$$

I think it's fairly odd to see the public key share being calculated like this. I bet you expected to see $d_i$ in there!

There's good reason for it not being used, though. We'll return to this statement later, because we'll need to define a couple things in order to understand what's really happening.

Once all the shares are public, then every participant can calculate the global public key independently:

$$Q = \sum_{i=1}^m Q_i$$

To wrap things up, here's a brief summary for this step:

Key generation involves parties communicating with each other, generating pieces of a shared private key. No single player knows the shared private key. A public key that is associated with the shared secret is also calculated.

With all the keys in place, all that remains is to sign.

Signing a Message

The first thing that we'll need is a message to sign. This is not trivial though, because everyone needs to agree on a message. We'll not cover how this happens — let's just assume everybody knows the message $M$ being signed.

In ECDSA, a signer would typically choose a random nonce $k$, and calculate a challenge $R = [k]G$ accordingly, producing a signature like this:

$$s = k^{-1}(H(M) + d.r) \ \textrm{mod} \ n$$

But as we've already seen, this is not how threshold cryptography tends to operate. Instead, a group of $t$ signers will communicate with each other in order to produce a signature. And the first thing they'll need, is a nonce.

Luckily, we already have a tool to generate a distributed value: DKG! Let's just say that signers execute a round of DKG, obtaining a share $k_i$, and an associated challenge:

$$R_i = \sum_{i=0}^m R_i$$

For the computation of the signature, everyone will use the x-coordinate of $R$, which we'll denote $r$.

Building the Signature

As you can probably guess by now, signature generation is also done in shares. And again, the idea is that only when a certain number of shares is available, we'll be able to produce a valid signature through the aggregation of these independently calculated parts.

Our requirement is the following: the signature shares $s_i$ should interpolate to the final signature $s$ — which should pass verification when using the public key $Q$. The most natural thing to do here, is to adapt the expression for $s$ so that it uses shares of its components instead:

$$s_i = k_i^{-1}H(M) + k_i^{-1}d_i.r \ \textrm{mod} \ n$$

But does this make sense? Here, we have an addition, multiplications, and even modular inverses. It doesn't feel obvious to assume that this will work just like that.

It seems only fair that we examine this expression and check that it works properly. And really, it's not as complicated as you'd imagine. Let's take it slow, one step at a time.

Interpolating Additions

To start us off, let's say that we have two polynomials $a(x)$ and $b(x)$. If we evaluate them at different values $i$, we get sets of points of the form $(i, a(i))$ and $(i,b(i))$. For convenience, let's just denote them $a_i$ and $b_i$:

$$a_i = (i, a(i)) b_i = (i, b(i))$$

We know that any subset of t points of these points allows us to interpolate back the original polynomials. And if we define the independent term of $a(x)$ to be $a$, we could write that:

$$a \leftarrow \textrm{interpolate}(a_1, ..., a_t)$$

As a reminder, in the context of secret sharing, we're usually interested in the independent term. This is why when we say that we interpolate some values, we may refer to the output as just this independent or zeroth coefficient, and not to the entire polynomial. But really, the full output is the entire polynomial!

Similarly, let's assume we have points $b(x)$ has independent term $b$, and so:

$$b \leftarrow \textrm{interpolate}(b_1, ..., b_t)$$

Now,what happens if we add the polynomials $a(x)$ and $b(x)$?

Click to zoom

We can add term by term, and we end up with a polynomial with the same degree as the originals ($t - 1$), but where the independent term is $g = a + b$. Also, since $g(x) = a(x) + b(x)$, then all the points that interpolate to $g$, which are $(i, g(i))$, can be calculated as $a_i + b_i$. And so:

$$g \leftarrow \textrm{interpolate}(a_1 + b_1, ..., a_t + b_t)$$

And that's awesome! This means that we can essentially add shares of a polynomial, and when interpolating, we'll get as the result the sum of the shared secrets. Neat!

Now we can analyze the public key calculation. Remember that the share $d_i$ is calculated as the sum of the $f_j(i)$ values.

Because of this, $d_i$ is essentially a share of a summation of polynomials, whose independent term will be the sum of all the $a_{i,0}$ terms. Which means, the result of interpolating all the $d_i$ will yield that summation!

Click to zoom

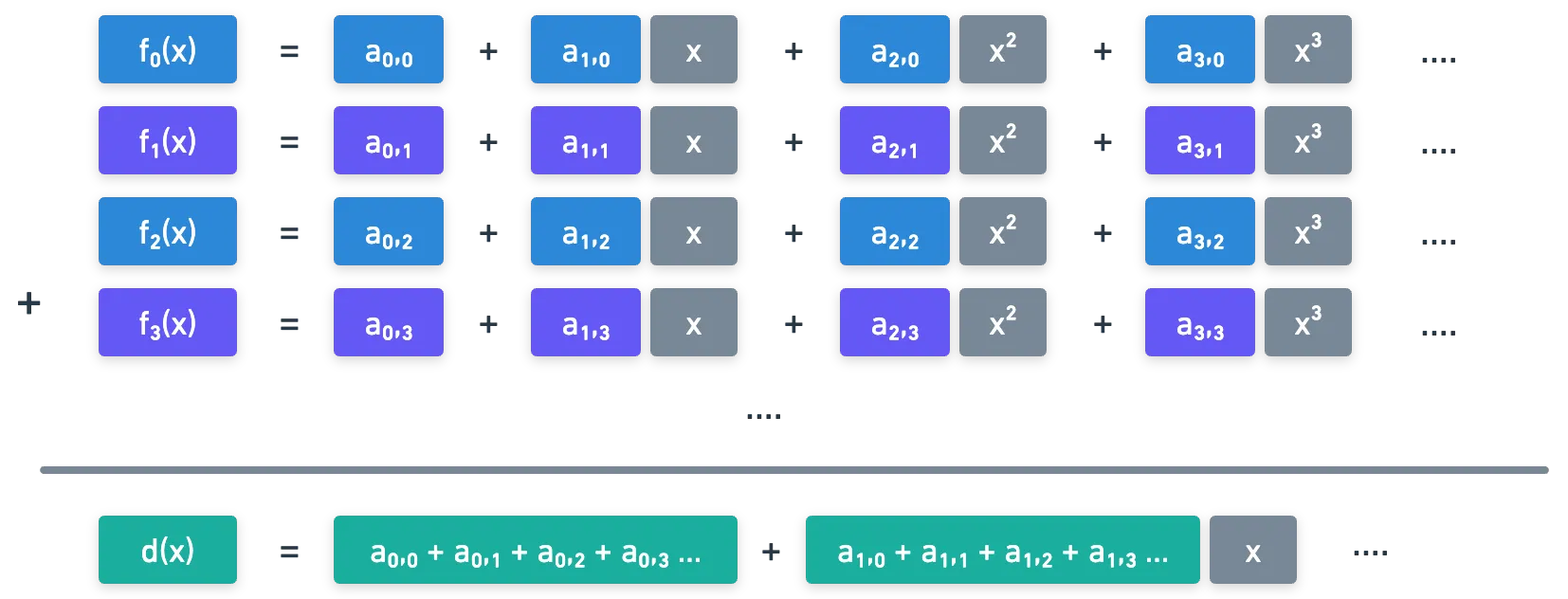
And that's the reason why the public key is calculated the way it is. Everything checks out!

$$\sum_{i=0}^m a_{i,0} \leftarrow \textrm{interpolate}(d_1, ..., d_m)$$ $$Q = \left [ \sum_{i=0}^m a_{i,0} \right ]G = \sum_{i=0}^m [a_{i,0}]G$$

Interpolating Products

Products are slightly trickier. When multiplying $a(x)$ and $b(x)$, the resulting polynomial $h(x)$ will have double the degree. And because of this, we need twice as many points for interpolation:

$$h \leftarrow \textrm{interpolate}(a_1.b_1, ..., a_{2t-1}.b_{2t-1})$$

And this is not really optimal, because now we need more values to interpolate, which means more communications between peers.

Regardless of this inconvenience, the good news is that this behaves the way we expect it to: when multiplying $h(x) = a(x)b(x)$, the independent terms are also multiplied, and our values $a_ib_i$ will also interpolate to $h = ab$!

Also worth mentioning: when multiplying shares by a constant, the resulting interpolation will also be multiplied by it:

Click to zoom

So if we take our shares to be $(i, k.a_i)$, then interpolation will yield $k.a$. Pretty straightforward, right?

Alright, we only have one more case to analyze. The pain and suffering will end promptly, I promise.

Interpolating Inverses

Really, all we're missing is handling that wretched modular inverse. What we want is to produce values ${k_{i}}^{-1}$ that, when interpolated, yield $k^{-1}$. This is going to take a couple steps. Yeah.

• First off, everyone will run a round of VRSS to produce shares $\alpha_i$. Of course, these shares interpolate like this:

$$\alpha \leftarrow \textrm{interpolate}(\alpha_1, ..., \alpha_m)$$

• Next, every participant will calculate and broadcast:

$$\mu_i = \alpha_i.k_i$$

• Since $\mu_i$ is the result of a multiplication, upon receiving $2t-1$ shares, anyone could interpolate this value:

$$\mu \leftarrow \textrm{interpolate}(\mu_1, ..., \mu_{2t-1})$$

• Finally, each participant calculates ${k_{i}}^{-1}$ in this fashion:

$${k_{i}}^{-1} = \mu^{-1}.\alpha_i$$

How does this wizardry work, you ask? Well, consider this: $μ^{-1}$ acts as a constant term when interpolating the ${k_{i}}^{-1}$ values. And because of this, we end up with:

$$\mu^{-1}.\alpha \leftarrow \textrm{interpolate}({k_1}^{-1}, ..., {k_{2t-1}}^{-1})$$ $$\mu^{-1}.\alpha = k^{-1}.\alpha^{-1}.\alpha = k^{-1}$$

And just like magic, we have built values that interpolate to the inverse of $k$!

That's all we're going to need! Let's check back on our signature calculation with our freshly-found conclusions.

Back to Signing

If we could reconstruct every shared secret, then the signature calculation would happen as in standard ECDSA:

$$s = k^{-1}H(M) + k^{-1}dr \ \textrm{mod} \ n$$

But in practice, we don't want that to happen — and we only have shares. And so we asked ourselves whether this:

$$s_i = {k_i}^{-1}H(M) + {k_i}^{-1}d_ir \ \textrm{mod} \ n$$

also interpolated to $s$. And the answer is a resounding yes, because we're only dealing with additions, products, and inverses — and we already know how these behave.

Perhaps the only problem here is that since we're dealing with a product of shares (the ${k_i}^{-1}d_ir$ term), we'll require like $3t-2$ shares to interpolate. But leaving that aside, we're sure that interpolating the $s_i$ values will yield the expected value of $s$!

Different protocols may make use of various techniques to try and mitigate the need for extra points for interpolation — and ideally, we'd want to keep that number as close to $t$ as possible. Also, the fewer communication steps are needed, the better.

To wrap things up, when each participant calculates their share $s_i$, they simply broadcast it. And when enough shares are available, anyone can interpolate, produce, and output $s$.

And there you have it! Simple, right?

I'm joking, of course — this is anything but simple. But the general idea is what's really the key takeaway:

During signing, parties again communicate with each other, generating pieces of a shared signature. When enough pieces are available, the final signature can be constructed; with less pieces than needed, it's simply not possible.

Verification happens as usual, because the output of the signature is simply the pair $(r, s)$.

Summary

I reckon this is the most technically-packed article I've written so far. I tried my best to keep it simple, but there are some things that we just can't avoid explaining. At the very least, I hope this sheds some light on some aspects that, from my experience, are not usually explained in detail.

🔥 Important: There's actually a pretty big vulnerability in the process I described, where private key shares are leaked when sharing $s_i$.

This is addressed in the paper I used as a guide, and the solution is actually quite simple. So please, don't go using this article to construct your threshold signatures — and maybe refer to the actual paper instead!

Designing these kind of Multi Party Computation protocols, where there's communication between parties, requires considering that malicious activity may exist. So in general, these protocols are filled with disqualification rounds, proofs of correctness, maybe even some encryption, and other fun stuff. Really, they are a consolidation of many different techniques, and tend to be complex.

Multi Party Computation is, in general, quite complex.

This is really the simplest scheme I could find in terms of what tools are needed, and is presented mostly in the hopes of illustrating the main components of these techniques. And this means that the more tools we can accrue, the easier it will be to craft more complex schemes.

Having said that, our journey will continue by presenting yet another extremely powerful tool, that will unlock new types of functionality: pairings. See you on the next one!