Cryptography 101: Homomorphisms and Isomorphisms

This is part of a larger series of articles about cryptography. If this is the first article you come across, I strongly recommend starting from the beginning of the series.

So far, our basic understanding of groups has proven useful enough to design cryptographic schemes that accommodate to a lot of needs — encryption, signatures, (and some exotic variants), proofs, commitments, verifiable randomness, etc.

I believe the time is ripe for us to further our understanding of group structures a bit, and while doing so, uncover a new set of cool cryptographic primitives.

You may have heard about homomorphisms and isomorphisms already. But what are these funny-named things, anyway?

Homomorphisms in a Nutshell

In general, a homomorphism is a function or map that preserves algebraic properties.

Recall that when working with groups, we only have a set and an operation. So a group homomorphism really maps elements of one group to another group, where the properties of the operation are preserved.

All this mumbo-jumbo can be reduced to this: if a and b are elements of a group, then an homomorphism f should behave like this:

$$f(a+b) = f(a) + f(b)$$

A great example of an homomorphism happens when we take an elliptic curve group with generator $G$ and order $n$, and the additive group of integers modulo $n$. And we just define:

$$f: \mathbb{Z}_n \rightarrow \langle G \rangle \ / \ f(x) = [x]G$$

We can easily see that addition is preserved:

$$f(a) + f(b) = [a]G + [b]G = [a + b]G = f(a + b)$$

Isomorphisms

Notice that in the case above, there's a one-to-one correspondence between elements of both groups. This need not always be the case: if we had chosen the integers modulo $q$ instead, with $q > n$, then at least two integers would share the same functional value.

In the case that there is in fact a one-to-one correspondence, then in theory we could use $f$ to map $\mathbb{Z}_n$ to $\langle G \rangle$, and its inverse $f^{-1}$ to map $\langle G \rangle$ to $\mathbb{Z}_n$.

In mathematical terms, this means that f is a bijection. You know, just in case you want to be more precise about it!

When this happens, we say that $f$ is an isomorphism instead of an homomorphism. And the groups are said to be isomorphic.

For all we care in terms of group theory, isomorphic groups are essentially the same group in disguise, for we can find a function that lets us transform one group into the other, and vice versa.

Why Should I Care?

Ah, the million-dollar question.

The idea of groups being homomorphic or isomorphic is very interesting, because moving back and forth from the chosen groups means that we can perform operations in either of them. And this allows us to do some magic. We'll see that in action in a minute.

Before jumping into an example though, I want to clarify some notation you may come across. If you check for instance this page on ElGamal's cryptosystem (an algorithm we'll look at in just a minute), you'll notice that they don't seem to use addition when working with groups. Instead, they use multiplication, and exponential notation:

$$y = g^x$$

Huh. This doesn't resemble our previous examples. How so?

The key to understand this is to see things under the lens of isomorphism. Take a look at these two groups:

$$\mathbb{Z}_5 = \{0, 1, 2, 3, 4\}$$ $$G_5 = \{1, g, g^2, g^3, g^4\}$$

If we just grab pen and paper and match element by element, we can clearly see that there's a one-to-one correspondence. Formally, the relation has the form:

$$f(x) = g^x$$

We say that the second group is multiplicative — notice that addition of elements in $\mathbb{Z}_5$ is replaced by multiplication of elements in $G_5$:

$$f(a + b) = g^{a+b} = g^a.g^b = f(a).f(b)$$

This is totally acceptable, since the operations in both groups are not necessarily the same.

So yeah, if you ever see the multiplicative notation while looking at a group-based system, bear in mind that an additive version can also probably be formulated by means of this isomorphism.

Homomorphic Encryption

Okay, enough formalisms. Let's get to the good stuff.

Suppose you want to perform a sum of two integers, modulo $q$. But these numbers are encrypted. Normally, you'd have to decrypt both numbers, and add them. And if you want to store the encrypted result, you'd have to re-encrypt.

But what if we could skip the decryption entirely?

This is exactly the goal of homomorphic encryption: performing operations on protected, private data, but obtaining the same result as one would get by operating with the plain, unprotected data, and encrypting later.

Click to zoom

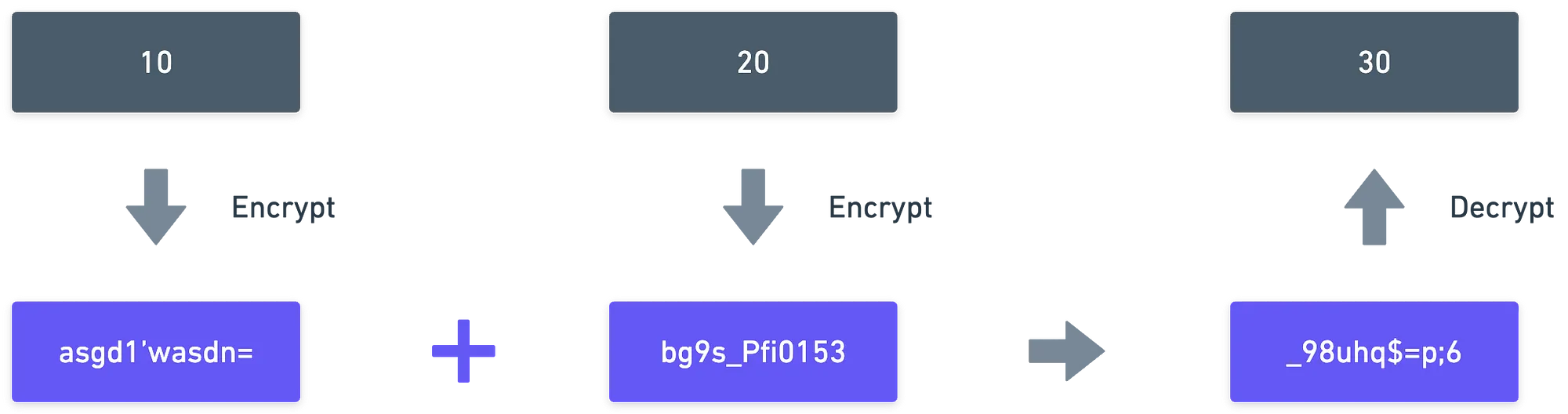
And that's awesome, because we can save ourselves the time of executing decryption operations — which are expensive — , while also preserving privacy of the data.

In theory, at least. There are some nuances around this, as we'll discuss in a minute. But the privacy part is cool, though!

So, how do we achieve this kind of functionality?

ElGamal Encryption

This is one of the simplest cryptosystems out there. In spite of it's simplicity, the encryption function has a very nice property: it's homomorphic!

Thus, we can perform operations of the encrypted data. Let's see how it goes.

As always, we'll start with Alice having a private key $$, which she uses to calculate a public key $Q = [d]G$. And yeah, $G$ is your typical elliptic curve generator.

Let's say Bob wants to encrypt a message for Alice, knowing her public key $Q$. For this to work, we must assume that the message is a point in the elliptic curve, $M$. And this can be obtained by passing the original message through a reversible function (hashing won't do).

We won't cover how to do that first step now — let's just assume we know how to do it.

Then, Bob follows this procedure to encrypt:

• He chooses a random integer r, and computes $R = [r]G$.
• After that, he calculates a mask (as usual) as $[r]Q$.
• Finally, he adds the mask to the message, so $C = M + [r]Q$.

The obtained ciphertext is $(R, C)$. To decrypt, Alice has to:

• Compute $[d]R$, which will be exactly equal to the mask $[r]Q$.
• Subtract the mask from $C$, so $C - [r]Q = M$.

Since we're being more precise now, we can say that subtracting is really adding the additive inverse of the subtracted value. It's just easier to say "subtract".

The encryption part of this process can be expressed as a function that takes a message $M$, and some randomness $r$, and outputs a ciphertext:

$$\varepsilon: \langle G \rangle \times \mathbb{Z}_q \rightarrow \langle G \rangle \times \langle G \rangle \ / \ \varepsilon(M,r) = ([r]G, M + [r]Q)$$

And this will be our homomorphism.

Imagine you encrypt $M_1$ with randomness $r_1$, and $M_2$ with randomness $r_2$. What happens if we add the encrypted results?

$$\varepsilon(M_1, r_1) + \varepsilon(M_2, r_2) = ([r_1]G, M_1+[r_1]Q) + ([r_2]G, M_2+[r_2]Q)$$ $$= ([r_1 + r_2]G, M_1+M_2+[r_1 + r_2]Q) = \varepsilon(M_1 + M_2, r_1 + r_2)$$

And boom! The result is the same as if we had summed the messages (and randomness) first!

Just like magic.

Observations

The scheme presented above is just about as simple as it gets. And although this example is very illustrative, it's not perfect by any means, and there are a thing or two we must say about it.

Encodable Messages

First, notice that the message we can encrypt is related to the group order, $n$. Remember that the group order means the number of elements in the group, so there's only finitely many ($n$, to be precise) different points in the group.

Since we're required to reversibly encode our message to a point $M$, then this means that each point $M$ corresponds to a unique message — so there's only n unique messages we can encode.

And this is, in turn, means that we cannot encode a message of arbitrary length. We could think of clever strategies to separate a message in "chunks", but this could undermine the homomorphic aspect of our scheme.

But this doesn't mean that the technique has no value — for instance, think of the messages as private balances. We could deal with a maximum representable balance, could we not?

Partial Homomorphism

On the other hand, this homomorphic encryption only supports one operation. And this is to be expected, since we're working with groups. So if the group operation is addition, then we can't do multiplication. And thus, this is known as Partial Homomorphic Encryption, or PHE.

If we can support both addition and multiplication, then our scheme would be fully homomorphic — and we would talk about Fully Homomorphic Encryption, or FHE for short.

Crafting a fully homomorphic encryption scheme is no easy task — and groups simply won't do. We'll require a different mathematical structure to tackle this, one that supports two operations. When that's our requirement, we need to jump into the domain of ring theory, an endeavor we will pursue later in the series.

Zero-Knowledge Proofs

Picture an application with private balances. You can decrypt your own balance, but whoever process a transfer request can't. Therefore, you need to somehow prove to the processor that you:

• Know your balance, and the amount to transfer
• Have enough balance to cover the transfer

But you need to do this without revealing the values, because the whole point of the application is to keep balances private!

In order to do this, we'll need to couple our homomorphic encryption efforts with Zero-Knowledge Proofs (ZKPs). And generally speaking, ZKPs tend to be computationally expensive — so the benefits of not having to decrypt are somewhat balanced out because of this. Nevertheless, privacy of the data may be required — for instance, homomorphic encryption is an attractive solution for privacy on public networks, such as Blockchains.

Summary

This time around, we went a little deeper into the mathematics, which ultimately allows us to better understand the structures that underly our constructions.

We saw a (partially) homomorphic encryption scheme in action. Of course, ElGamal's is not the only system that has this homomorphism property. Other group-based schemes exist, such as the Benaloh cryptosystem or the heavily-cited Paillier cryptosystem.

We've come a long way. For now, we'll put a stop to our exploration of elliptic curve cryptography (ECC). But this is not the end of the journey, by any means. Turns out that elliptic curve groups work very nicely with another construction that allows some very cool cryptography. We'll get into that soon.

However, there's a topic I want to touch on before that: polynomials, and the possibilities they offer. This will be the topic for the next article!