Las Crónicas de ZK: Modelos de Cómputo

¡Hola! ¡Me alegra que hayas sobrevivido al artículo anterior!

No hace falta que te hagas el fuerte, sé que probablemente fue mucho. Perdón por eso.

Quizás la conclusión más importante de nuestro último encuentro fue que pudimos demostrar que verificar un cómputo general de manera eficiente es posible. Pero entonces, también mencionamos que rara vez escribimos programas como circuitos aritméticos. O sea... Cada uno con lo suyo, pero ¿qué clase de loco tendrías que ser para escribir programas como compuertas de suma y multiplicación conectadas?

En su lugar, usualmente usamos niveles más altos de abstracción, en forma de lenguajes de programación. Usamos bucles, condicionales, funciones. ¿Qué hacemos con esos?

¿Qué hago con mi programa en Python, bro?

Bromas aparte, la pregunta real es: ¿por qué circuitos? Y aunque hemos visto algunos buenos puntos a su favor, como su descomponibilidad, es difícil sacarse la idea de que querríamos probar cosas sobre otros tipos de programas.

Así que hoy, quiero guiarte a través de las conexiones entre estos diferentes modelos de cómputo. Estas revelarán algunos aspectos fundamentales de la computación verificable en general, y abrirán un mundo de posibilidades.

No sé tú, ¡pero esto suena emocionante! ¡Vamos!

Computación

Nuestro viaje de hoy comienza con una pregunta simple: ¿qué significa realizar una cómputo?

A primera vista, esto podría parecer una pregunta tonta. Escribes código, la computadora lo ejecuta, obtienes un resultado. ¿Dónde está la complejidad en eso?

Pero si lo pensamos con más cuidado, las cosas empiezan a ponerse interesantes. Por ejemplo, escribir un programa para sumar dos números en JavaScript no es lo mismo que escribir instrucciones en Assembly para sumar dos números. Tampoco es lo mismo escribir un circuito para este mismo propósito.

¿Son todos estos el mismo cómputo? Ciertamente se ven diferentes, usando una sintaxis diferente, operaciones diferentes, y quizás lo más obvio, diferentes niveles de abstracción. Pasamos de la simplicidad de una puerta de un circuito, a la arquitectura compleja de una CPU, a todas las locuras interpretativas de JavaScript.

Sin embargo, intuitivamente, todos estos ejemplos hacen lo mismo: ¡suman dos números!

Este asunto está en el núcleo mismo de la teoría de la computación: ¿qué significa que diferentes procesos computen lo mismo? Y más importante aún: ¿son algunos modelos de computación fundamentalmente mejores o más poderosos que otros, o son todos equivalentes en algún sentido?

No debería sorprendernos que haya toda una rama de las matemáticas (y la ciencia de la computación) dedicada a estudiar este tipo de preguntas sobre modelos de computación.

Teoría de la Complejidad Computacional

En resumen, la teoría de la complejidad computacional es el estudio de lo que puede y no puede ser computado de manera eficiente.

Uno de sus conceptos fundamentales es el de clases de complejidad: grupos de problemas con dificultad equivalente, para los cuales podríamos intentar encontrar algoritmos eficientes.

Así, podemos estudiar modelos de cómputo para resolver problemas en estas clases, en lugar de adaptarnos a problemas particulares.

Estos modelos para de cómputo son realmente abstracciones matemáticas que capturan la esencia de lo que significa "computar algo", independientemente de lenguajes de programación o hardware.

Acá van algunos de los principales modelos que estudia la teoría de la complejidad. Algunos de ellos seguro te sonarán familiares:

• Máquinas de Turing: básicamente el abuelo de los modelos de computación. Imaginemos una cinta infinita que contiene celdas, que a su vez contienen símbolos. La máquina apunta a una sola posición en la cinta en cualquier momento, y puede moverse a la izquierda o a la derecha. Dependiendo del valor del símbolo, y basándose en un conjunto simple de reglas, este puntero a la cinta puede moverse a la izquierda o a la derecha a otras ubicaciones, e incluso escribir en la cinta. Quizás te sorprenda que, a pesar de ser absurdamente simple, las máquinas de Turing pueden computar cualquier cosa que sea computable.
• Máquinas de Acceso Aleatorio (RAMs): un modelo más cercano a las computadoras reales, con direcciones de memoria a las que puedes acceder directamente. Esto es esencialmente cómo funciona tu laptop tras bambalinas.
• Cálculo Lambda: un enfoque puramente matemático donde todo es una función. Solo hay tres operaciones: definir funciones, aplicar funciones a argumentos, y sustituir variables. Sin bucles, sin declaraciones if, sin cambiar variables — ¡solo composición pura de funciones!

¡Y luego, están los circuitos booleanos y circuitos aritméticos de los que hemos estado hablando durante algunos artículos!

A pesar de verse tremendamente diferentes en la superficie, la mayoría de estos modelos resultan ser equivalentes de una manera profunda e intrigante.

El Teorema de Cook-Levin

En 1971, dos científicos de la computación llamados Stephen Cook y Leonid Levin probaron independientemente algo notable que tiene implicaciones profundas para nuestro análisis.

Para entender su teorema, primero necesitamos hablar sobre una clase de complejidad especial, llamada NP.

NP significa tiempo polinomial no determinista, y es la clase de problemas donde podemos verificar una solución rápidamente (en tiempo polinomial), pero encontrar dicha solución se considera difícil (al menos, toma más que tiempo polinomial).

Si estrujas un poco tu memoria, recordarás que ya hablamos de esto en el primer artículo, ¡cuando mencionamos el Sudoku!

Con esto, ahora podemos saltar al teorema de Cook-Levin. Aunque no lo vamos a probar, ¡porque eso tomaría mucho más que un solo artículo! Además, solo el enunciado nos dará mucho que procesar. Aquí va:

Cualquier problema en NP puede ser reducido a satisfacibilidad de circuitos en tiempo polinomial

¡Sí! ¿Recuerdas nuestro problema de satisfacibilidad de circuitos (CSAT)? No solo resulta ser un problema NP, sino que también es equivalente a cualquier otro problema NP que existe (tomando un factor de incremento polinomial en tiempo de ejecución).

La forma en que enmarqué la discusión entre satisfacibilidad de circuitos y evaluación de circuitos terminó pintando una imagen muy diferente sobre la importancia y generalidad de la satisfacibilidad de circuitos... ¡Eso no podría estar más lejos de la verdad, como ahora sabemos!

Así que al final, la satisfacibilidad de circuitos tiene un papel teórico central. Debido al teorema de Cook-Levin, podemos tomar cualquier problema NP, y convertirlo en una instancia de CSAT. El teorema garantiza que esto es posible, pero por supuesto, los mecanismos pueden variar.

Una vez que tenemos nuestra instancia de CSAT, podemos producir un circuito aritmético. Lo cual nos permite concluir:

Los circuitos aritméticos son un modelo universal para la computación acotada

¡Sí! Cualquier cómputo que nos importe puede ser expresado como un circuito aritmético. Esta es la razón principal por la que hemos estado estudiando circuitos hasta ahora, además de las características interesantes que poseen: son matemáticamente simples, descomponibles, posiblemente estructurados, y ahora además de eso, universales.

También hay otra consecuencia agradable de esto: podríamos usar CSAT como un punto de pivote para demostrar que cualquier par de problemas NP son equivalentes.

Click to zoom

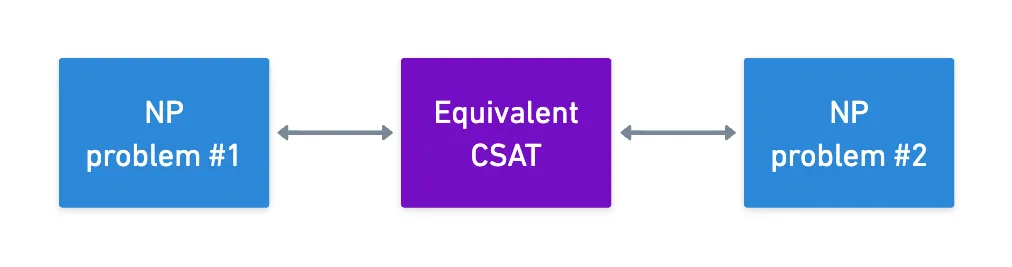
Lo realmente genial de esto es que potencialmente podríamos encontrar un sistema de pruebas muy eficiente para un problema NP particular, y podríamos al menos en teoría convertir cualquier otro problema NP a esa forma — por supuesto, con los costos de transformación asociados (que usualmente llamamos un factor de explosión, o blowup factor en inglés).

Esto sugiere una sutileza poderosa: con transformaciones apropiadas, ¡podemos aplicar cualquier algoritmo de prueba a cualquier problema!

Si esta es una buena estrategia o no... ¡Esa es otra historia!

Lenguajes y Problemas de Decisión

¡Bien! Hemos establecido exitosamente que los circuitos son universales.

Si bien esto tiene un valor teórico inmenso, hay un cambio sutil de perspectiva que necesitamos hacer explícito — uno que se volverá crucial a medida que nos adentremos más en los sistemas ZK.

Un Adelanto de ZK

Para motivar esto, profundicemos brevemente nuestra discusión sobre conocimiento cero desde el primer artículo.

Todavía es muy temprano para que definamos formalmente lo que entendemos por "conocimiento cero". Eso no significa, sin embargo, que no podamos empezar a acercarnos a la definición real a través de conceptos ligeramente más sofisticados.

Una cosa que no sabíamos en ese entonces es que podemos usar circuitos para representar cómputos. Ahora que lo sabemos, podemos definir aproximadamente qué significa ZK. Va así: un probador intentará convencer a un verificador de que conoce alguna entrada $w$ a un circuito dado de manera que la salida del circuito sea un valor específico:

$$\varphi(w) = 0$$

El valor de salida esperado usualmente es $0$. Y cualquier circuito se convierte fácilmente a este formato agregando una puerta extra que resta la salida esperada.

Lo que hace que esto sea conocimiento cero es que el verificador puede ser convencido sin nunca conocer $w$.

Suficientemente simple, ¿no?

Observemos que en la formulación anterior, al verificador nunca le importa realmente el valor real de $w$, solo que existe tal $w$, y esta pregunta solo tiene dos respuestas válidas: sí y no.

Los problemas planteados de esta manera se llaman problemas de decisión, y están en el extremo opuesto directo del tipo de problemas donde en realidad podríamos preocuparnos por encontrar una solución válida a un problema.

¡Por ejemplo, queremos encontrar una entrada que satisfaga un circuito!

Este tipo de problema se llama un problema de búsqueda, y supongo que podrían sentirse más naturales para la mayoría de las personas. Tenemos un problema, encontramos una solución que funciona, boom. ¿A quién le importan todas las soluciones posibles?

Bueno, ZK sí: ¡el verificador solo necesita saber que existe una solución válida, sin obtener conocimiento de su valor!

Además, los dos tipos de problemas están estrechamente relacionados: si puedes resolver el problema de búsqueda, obviamente puedes resolver el problema de decisión (¡porque has encontrado una solución!).

La otra dirección es un poco más complicada, pero en términos generales, si puedes resolver el problema de decisión de manera eficiente, a menudo también puedes resolver el problema de búsqueda de manera eficiente. Esto se hace a través de una técnica llamada auto-reducibilidad.

En este sentido, la teoría de la complejidad computacional estudia los problemas de decisión usando un marco matemático muy riguroso, llamado lenguajes.

Lenguajes

Antes de que preguntes: no, esto no tiene nada que ver con lenguajes de programación como Python o Rust.

Un lenguaje es simplemente un conjunto de strings que codifican "instancias sí" de un problema.

Creo que esto es más fácil de entender con un ejemplo. Consideremos el siguiente problema: se nos da algún número, y nos preguntamos "¿es ese número primo?".

Por supuesto, podrías seguir adelante y escribir un algoritmo para determinar esto. Pero conceptualmente, hay algo más que podemos hacer. Definamos el conjunto $\mathcal{L}_p$ como:

$$\mathcal{L}_p = \{2,3,5,7,11,13,17,19,23,...\}$$

O quizás de manera más reducida:

$$\mathcal{L}_p = \{n : n \ \textrm{es primo}\}$$

Debería estar completamente claro lo que queríamos decir: este es exactamente el conjunto de todas los valores (en este caso, números) para los cuales la respuesta a nuestra pregunta original es sí. Y verificar si un número es primo, siempre que conozcamos este lenguaje de antemano, es tan simple como verificar si el número pertenece a $\mathcal{L}_p$.

Y sé lo que estás pensando: ¿cuál es el punto?

En nuestro ejemplo, ¿cómo es que encontrar $\mathcal{L}_p$ (que por supuesto es un conjunto infinito) es más fácil que determinar si un solo número es primo?

Sí, podría parecer un formalismo sin sentido, pero los lenguajes son en realidad bastante poderosos. Al enmarcar problemas en estos términos, podemos:

• Hablar con precisión sobre lo que significa resolver un problema (encontrar un valor que pertenece a $\mathcal{L}$).
• Definir clases de complejidad como conjuntos de lenguajes.
• Razonar sobre reducciones entre problemas.

Por ejemplo, nuestro problema general de satisfacibilidad de circuitos puede ser planteado como un lenguaje:

$$\mathcal{L}_{\textrm{CSAT}} = \{\phi : \exists x \ \textrm{s.t.} \ \phi(x) = 1\}$$

Este es el conjunto de todos los circuitos que tienen al menos una entrada satisfactoria. El problema de decisión entonces pregunta si un circuito particular $\phi(X)$ es satisfacible, ¡lo cual es equivalente a preguntar si pertenece al lenguaje!

Alternativamente, podríamos definir otro lenguaje para un circuito específico, como el conjunto de todas sus entradas satisfactorias. En ese caso, ¡la solución a #SAT (el problema de conteo) simplemente devuelve el tamaño de dicho lenguaje!

Testigos

Ahora, aquí es donde las cosas se ponen interesantes para ZK.

Mencionamos que los problemas NP son aquellos para los cuales podemos verificar una solución rápidamente. Y dado que ya nos hemos movido a la teoría formal, quizás ahora sea un buen momento para definir con más precisión lo que queremos decir por verificar.

En el marco de lenguajes, la verificación involucra tres piezas:

• La instancia del problema ($x$), que representa el problema que estamos tratando de resolver (es decir, un rompecabezas de Sudoku específico, un circuito dado).
• El testigo ($w$), que es solo una pieza de evidencia que prueba que $x$ tiene una solución.
• El verificador ($\mathcal{V}$), que es un algoritmo que verifica si $w$ es evidencia válida para $x$.

Con estas piezas, podemos formular lo siguiente: un lenguaje $\mathcal{L}$ está en NP si existe un verificador de tiempo polinomial $\mathcal{V}$ y un testigo de tamaño polinomial $w$ tal que:

$$x \in \mathcal{L} \iff \exists w : \mathcal{V}(x, w) = 1$$

Sí... ¿Qué diablos es eso?

Relájate, te tengo cubierto. En español simple, lo que esto está diciendo es que para problemas NP, una solución a $x$ puede ser verificada en tiempo polinomial (así que, rápidamente) por el verificador $\mathcal{V}$ gracias al uso del testigo $w$.

Pero ¿qué podría ser este $w$? Nuestros dos ejemplos hasta ahora revelan:

• En Sudoku, $x$ es una cuadrícula parcialmente llena, $w$ es la solución completa al rompecabezas, y $\mathcal{V}$ simplemente verifica que todas las filas, columnas y cuadrados contengan todos los números del $1$ al $9$.
• En CSAT, $x$ es el circuito con el que estamos tratando, $w$ es una entrada que satisface el circuito (así que, produce $1$ o $\textrm{TRUE}$), y $\mathcal{V}$ funciona evaluando el circuito con entrada $w$, y verificando la salida obtenida.

La verificación es obviamente rápida en ambos casos. Sin embargo, los testigos podrían levantar algunas cejas: ¡son soluciones válidas completas al problema!

Espera... ¿Soluciones válidas? ¡Eso significa que el verificador aprenderá la solución al problema! ¿No rompe eso nuestra definición de conocimiento cero?

En lugar de entrar en modo pánico, supongo que es mucho mejor para nuestra salud mental hacernos esta pregunta fundamental: ¿es posible que el probador mantenga $w$ privado, pero de alguna manera convenza al verificador de que $x \in \mathcal{L}$?

Algo como: "Conozco una entrada a este circuito ($w$) que hace que la salida sea $\textrm{TRUE}$, pero no te voy a decir cuál es... ¡Y aún así puedo convencerte!".

Por supuesto, esto es absolutamente posible (¡no estaríamos aquí de otra manera!).

El punto clave es que podemos intentar probar que $w$ existe, sin revelarlo. Y esto es el aspecto esencial que define el conocimiento cero.

Además, el testigo no siempre tiene que ser la solución completa. Solo necesita ser evidencia suficiente. Los sistemas ZK avanzados usan testigos comprimidos o inteligentemente estructurados, lo que ayuda a hacer las pruebas más eficientes.

Por desgracia, todo esto es más fácil decirlo que hacerlo. Empezaremos a ver formas de hacer esto en su momento, pero este nuevo marco de lenguajes al menos nos da una forma más limpia de formular nuestro objetivo:

Probar que $x$ pertenece al lenguaje, mientras ocultamos el testigo $w$.

En otras palabras: ¡probar que un circuito es satisfacible, sin revelar la entrada satisfactoria real!

De la Teoría a la Práctica

Bien, hemos cubierto mucha teoría. Los circuitos son universales, los lenguajes nos dan un marco formal, los testigos ayudan con ZK, sí, sí... ¿Pero cómo me ayuda esto realmente a probar cosas? ¿Cómo funciona esto realmente en la práctica?

Bueno, después de todo este bombardeo teórico, aquí hay una buena noticia: no escribimos circuitos aritméticos manualmente.

¡Eso sería una locura!

El teorema de Cook-Levin que vimos antes nos permite hacer algo bastante agradable: podemos construir pipelines de compilación que transforman cualquier cómputo en una forma probable.

Para esto, los sistemas ZK modernos usan una arquitectura frontend-backend.

En pocas palabras, lo que haces es escribir tu cómputo de una manera más natural, usando ya sea:

• Lenguajes de Dominio Específico (DSLs) como Circom o Noir, donde escribimos código tipo circuito que sigue siendo más legible para humanos que las puertas de mierda.
• Lenguajes de propósito general, como Rust o Python.

Los frontends procesan estas representaciones, y las transforman en formas adecuadas que son simplemente representaciones algebraicas de circuitos, como R1CS, aritmetización PLONK, y AIR.

¡No te preocupes, veremos qué son esos más tarde!

Luego, los backends toman estas representaciones de circuitos y usan sistemas de prueba (como GKR, u otros que exploraremos más tarde) para generar las pruebas ZK reales.

Por supuesto, ¡todo este pipeline no sería posible si no fuera por los resultados teóricos que cubrimos hoy!

Cook-Levin garantiza que cualquier cómputo puede ser reducido a un problema CSAT, lo que nos da una enorme versatilidad. Por supuesto, estas transformaciones tienen costos, y los diferentes sistemas de prueba hacen diferentes compensaciones, o incluso pueden estar adaptados para situaciones específicas — así que tendremos que ser cuidadosos con nuestras selecciones.

Pero bueno, ¡al menos tenemos algo de margen de maniobra!

Resumen

¡Eso es suficiente teoría por hoy!

Nuestra simple pregunta inicial nos llevó por un camino teórico intenso en la teoría de la complejidad computacional — el estudio de diferentes modelos de cómputo y sus relaciones.

Esto reveló cosas importantes: los modelos son fundamentalmente equivalentes, y los problemas pueden convertirse entre uno dentro de la misma clase de complejidad (hasta una explosión polinomial). En particular, el teorema de Cook-Levin muestra cómo cualquier problema NP puede ser reducido a satisfacibilidad de circuitos, lo que dice algo sobre la universalidad de los circuitos.

También introdujimos un marco crucial: lenguajes y testigos. Esta es una forma diferente de pensar sobre problemas. Podría parecer un poco extraño por ahora, pero es un conjunto poderoso de herramientas para pruebas formales. Usaremos lenguajes más adelante, pero por ahora, solo mantener su existencia en el fondo de tu mente es suficiente.

Si estás aquí después de todas estas cosas, ¡felicidades! Este es probablemente el salto teórico más difícil de la serie. Claro, necesitaremos hablar sobre otros conceptos teóricos más tarde, pero al menos para mí, esta fue la parte más complicada de escribir, o incluso de entender.

Así que la próxima vez, empezaremos a construir sobre todos los fundamentos que hemos cubierto hasta ahora, usando algunas ideas que probablemente se sentirán más familiares, y sin embargo, ayudarán a hacer que la computación verificable y los sistemas ZK sean realmente utilizables.

¡Hasta entonces!