Blockchain 101: Storage

This is part of a larger series of articles about Blockchain. If this is the first article you come across, I strongly recommend starting from the beginning of the series.

Last time, we went through a high-level introduction of Ethereum.

Although many of the ideas we discussed were new when compared to Bitcoin, they are actually quite fundamental in most Blockchain systems— especially the ability to create and execute these programs we call Smart Contracts.

The level of abstraction we’ve managed so far hides all the inner workings of Ethereum’s architecture. And that’s fine as a first approach, as some concepts feel very new and exotic, again, when compared with Bitcoin.

But you and I both know — you’re not here for the higher level of abstraction.

In the next few articles, we’ll be diving into Ethereum’s machinery, slowly uncovering its secrets.

To kick things off, let’s look at how data is stored.

Shall we?

State and Storage

The first thing we need to understand is how the state of the Blockchain is modeled in Ethereum, so that we can figure out strategies to store it. In this aspect, Bitcoin was much simpler: the state was just a list of available UTXOs.

Although storing these UTXOs has its ins and outs, conceptually, it’s pretty simple. We could picture this as a table containing the full state, like this:

Click to zoom

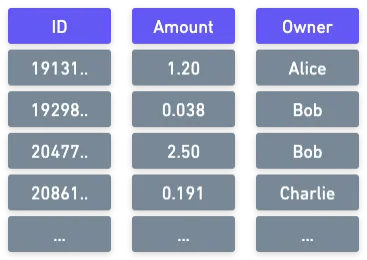
So, what about Ethereum? It clearly isn’t going to be this simple. State is an abstract concept to represent just about anything. We’ll need something a little more sophisticated than our simple conceptual table...

Since we already know we’re working with accounts, and basically the entirety of Ethereum’s state can be described in terms of the state of individual accounts, let’s ask ourselves: just what defines the state of an account?

In the previous article, we mentioned a couple noteworthy things:

• Accounts can have a native token (Ether) balance
• Accounts can either be an Externally Owned Account (EOA), or a contract account, containing code to execute

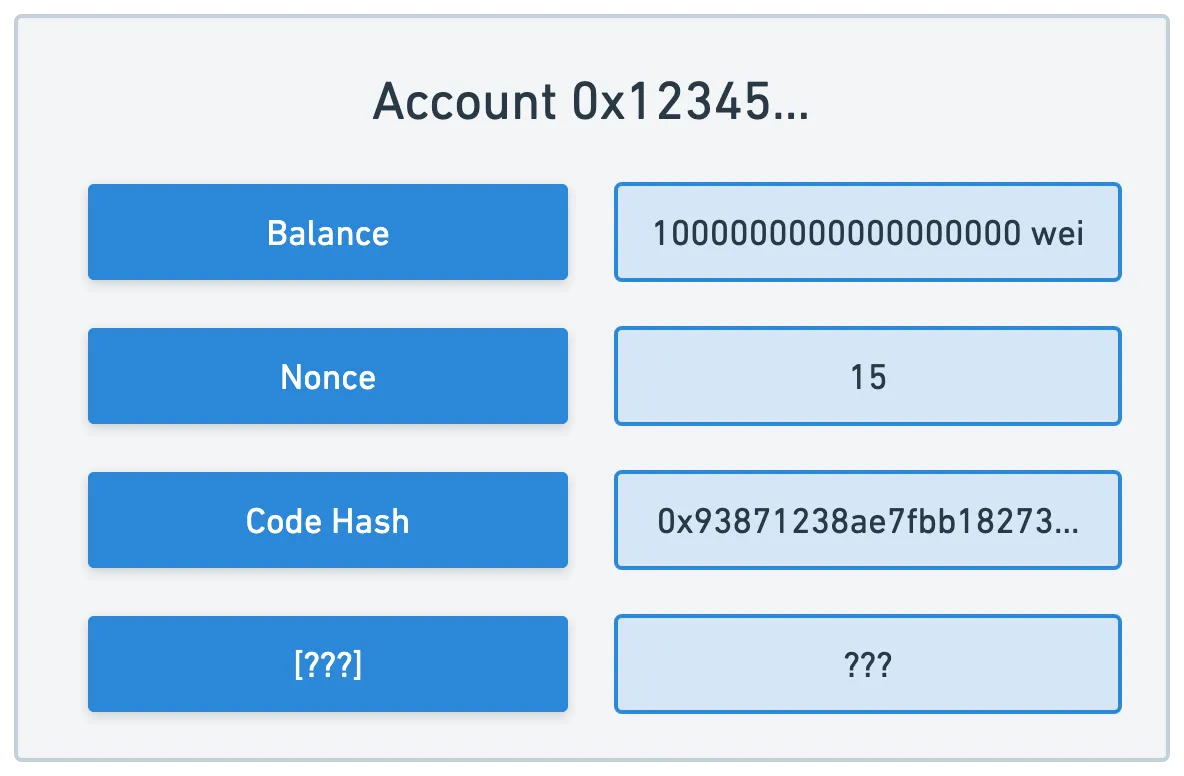
Plus, there are a couple more items that we need to throw into the mix. One such thing is a nonce, which is an incremental count of transactions. We also need another thing we’ll discuss in just a moment.

We can think of accounts as these pockets of data containing account information as a set of key-value pairs:

Click to zoom

Now, one thing that’s desirable (although we didn’t talk much about this in our pass through Bitcoin) is to have some sort of fingerprint for the entire state of the Blockchain, so that we can identify a state by a single value, and be sure that if anything at all changes, this fingerprint will change.

This is a useful way to tag or identify the current state of the Blockchain.

We already know of a structure that allows for this kind digestion process into a single root: Merkle trees!

But Merkle trees alone simply won’t make the cut in this scenario. In particular, they have two important shortcomings:

• They are not very practical for insertion (nor deletion) operations, as we need to take care of padding (making sure that the number of leaves is a power of $2$), and
• They offer no way to search for nodes, as there’s no built-in identification system

I believe the second point is of the most importance here: given an account’s address, we want to be able to quickly find its attributes.

To address these issues, a slightly different data structure is used to encode accounts: a Merkle-Patricia trie.

Finding a Suitable Data Structure

What we need is a structure that allows for some kind of indexing. Merkle trees have really simple incremental indices — these values are only used to keep leaves ordered, but say nothing about their content.

But there’s another structure that puts the identifier of a node at the center of its design: a trie.

Tries (also known as prefix trees) are, as you would expect from the name, special types of trees. Starting from the root node, each leaf is associated to an alphanumeric character. Because of this, following any one path in the tree will form a string of characters, one node at a time.

Click to zoom

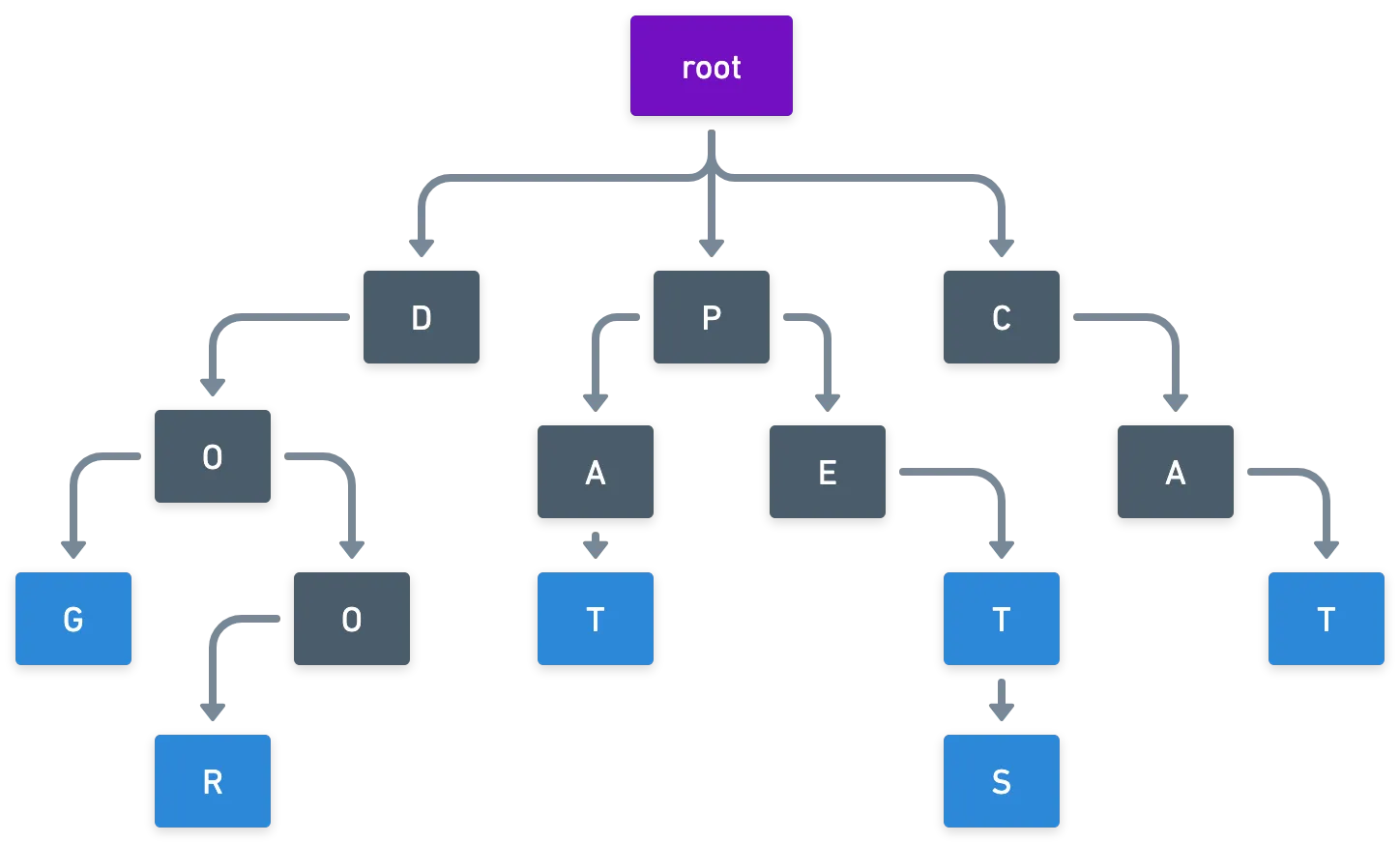
The cool part about this kind of structure is that finding a node by its index is as simple as traversing the tree one letter (node) at a time!

And of course, a terminal node will contain the information stored under the specified index.

Something that happens with these trees though, is that their depth is determined by the longest index, in terms of character length. And this may cause storage problems, because we need to keep track of a large number of intermediate nodes in memory. Also, nodes can potentially have a single child, which would pose a problem for us, for reasons we’ll see further ahead.

To try and remedy these situations, we can use a simple variation: a radix tree. Essentially, we condense nodes that have a single child into one node.

Click to zoom

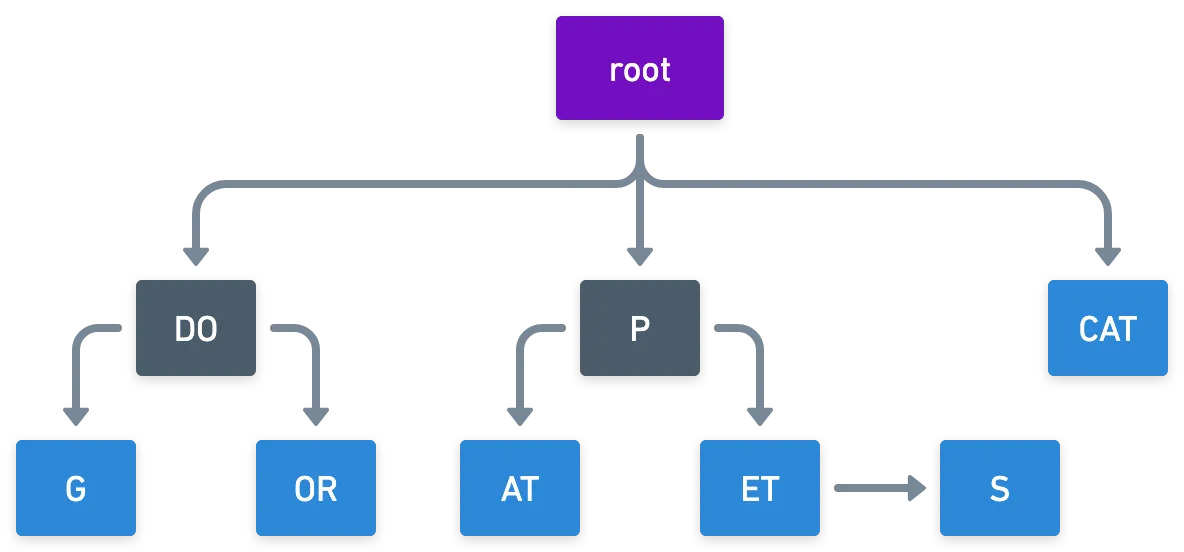
You can see insertions and deletions in action in this website.

One thing to notice is that there’s a maximum number of children a node can have. In the case of alphanumeric characters, a single node can have up to $62$ different children, one for each unique character. Unsurprisingly, this number is called the radix of the trie — which is determined by the “alphabet” we use, and not the structure itself.

Patricia Tries

All this to finally say:

Patricia tries are essentially radix tries with radix = 2, with a couple twists

Just for the sake of completeness: PATRICIA stands for “Practical Algorithm To Retrieve Information Coded in Alphanumeric”.

This means that the alphabet is binary — just the numbers $0$ and $1$ are used.

There are other subtleties to consider when constructing a Patricia trie, one of which is the inclusion of a skip value that makes traversals more efficient.

Lastly (and importantly), Patricia tries can be organized in such a way that there are no single-child nodes. In other words, every node will either be a leaf node (no children) or an internal node (two children).

While radix tries in general can have single-child nodes, it’s possible to enforce this no-single-child-nodes condition on any radix trie.

Here’s an example:

Suppose we want to organize these keys in a Patricia trie

• 10010000 (144)
• 10010100 (148)
• 10011000 (152)
• 10100000 (160)
• 11000000 (192)
• 11000001 (193)

Here’s what a Patricia trie may look like:

Click to zoom

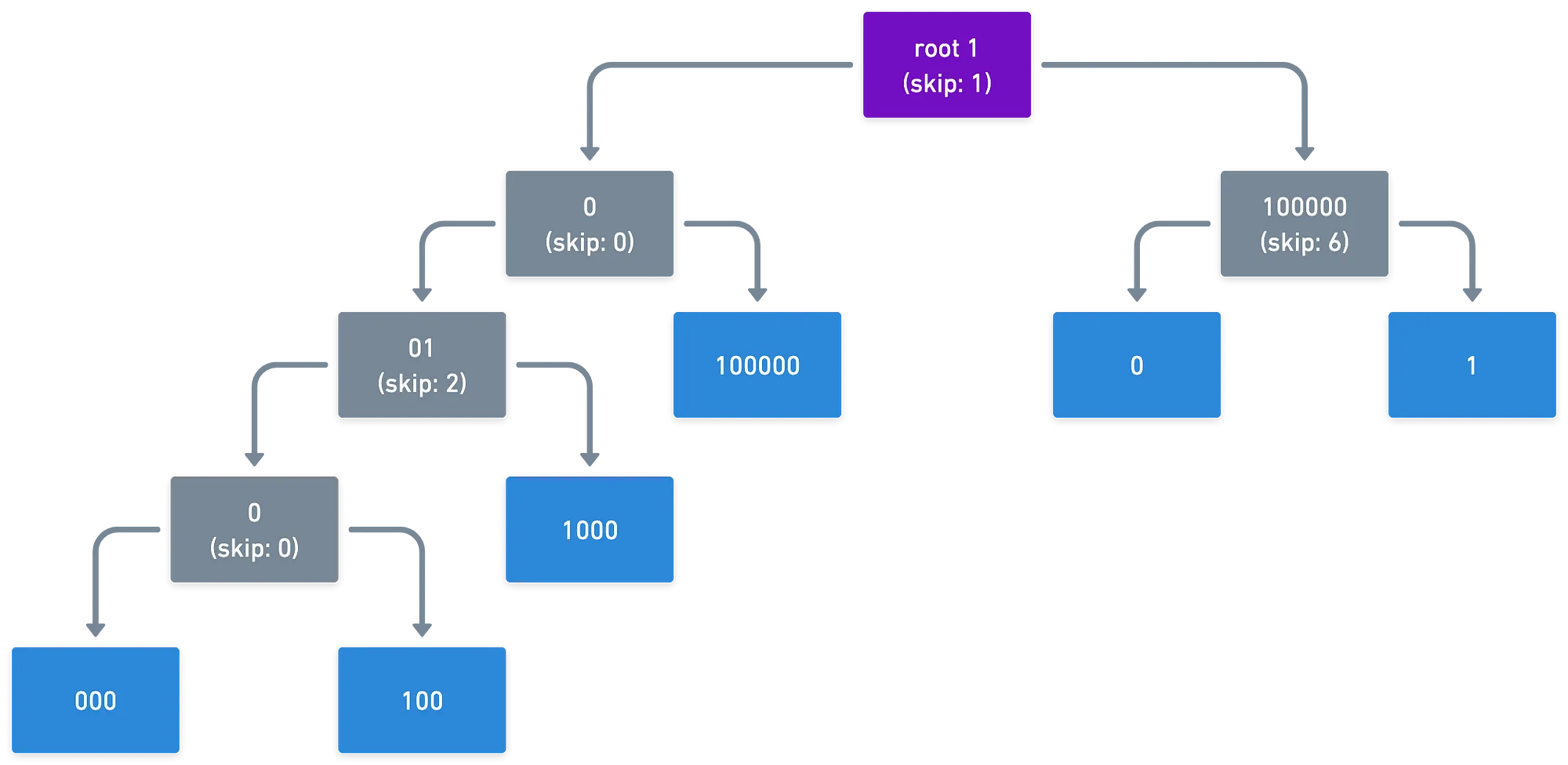
Patricia tries are very compact and memory-efficient, while also allowing for fast insertions and deletions, which is an interesting property for a system (like Blockchain) that needs to handle a constantly changing state!

Merkleizing It

All that remains is adding this sort of “fingerprinting” feature to Patricia tries that’s so important in Merkle trees. Can we combine the best of both worlds?

For sure! With two very simple considerations:

• The index or identifier for a node, which defines its placement in the tree, is determined by the address of an account
• Internal nodes — which have two children — keep track of the hash of the concatenation of its children’s hashes

Particularly, this hash consolidation on parent nodes “flows up” the tree, so that the root node will contain a hash that is unique to the tree, and depends on every single leaf, just like in Merkle trees!

A Caveat

Here’s a curveball: even though we’ve heavily suggested that Ethereum uses Patricia Merkle tries — and you’ll normally see documentation floating around the internet stating this — , the truth is that it doesn’t.

Ethereum currently uses radix tries, with a radix of $16$. Hex tries, we could say!

Despite not being technically correct, the community seems to have adopted the term “Patricia Merkle trie” anyway. We could at least say that we’re working with a modified version, but the reality is that they are just radix-16 Merkle tries, with the constraint of every node having either no children, or at least two (and up to $16$) children.

The above constraint enables Merkleization, so we don’t have anything to worry about in this aspect — internal nodes will always have enough children for the process to work. Neat!

Bloating

So we’ve settled on a structure to store accounts. At this point, we should note that the Modified Patricia Merkle tree will be hella big, because there are lots of accounts to keep track of.

And this means trouble — after all, the state trie has to be stored somewhere, and that place needs to have lots of available memory. This situation was baptized Blockchain bloating or state bloating, and it’s a concern that Blockchains are still trying to solve.

Ethereum’s team has full knowledge of this problem, and one of the major milestones in the evolution of this Blockchain is to try and reduce bloat, in a possible future event they call “The Purge”. Here’s a great post by the very mastermind behind Ethereum going into much more detail!

Also worth mentioning, there are other possible futures envisioned by the Ethereum team, with their own research being conducted. One such alternative was named "The Verge", which proposes switching the Patricia Merkle trie storage with another structure called Verkle trees, possibly combined with STARK proofs.

It’s a lot to take in — and I believe it wiser to start by understanding the current state of things!

Regardless, the information is stored in network nodes. But not every node needs to store this gigantic state — some of them are specialized for this purpose, and a little more. The type of nodes that store the state trie are full nodes, or archive nodes — while other, like pruned nodes or light nodes store only a portion (or none of) the state. All these nodes have different functions, which we may explore in future articles.

Storage... Where?

Up until now we’ve said that account data is stored in Patricia Merkle tries. But that’s not entirely true.

While it is true that the data structure is very useful to condense the entire state of the Blockchain into a single root, we’ve never mentioned where those tries live in storage. And the truth is, they aren’t stored as such.

Truth is that Ethereum uses a key-value database to store information.

I know, shocking.

Why go through all that trouble looking for a suitable data structure, then? Before we start pondering the meaning of life after this revelation, let’s consider the implications here.

Each account is represented by some identifier (i.e. an address), and some attributes — nonce, balance, etc. Patricia Merkle tries give us an elegant way to consolidate the data in the entirety of Ethereum’s accounts into a single root, which works wonders when checking for data consistency. But the trie says nothing about where each account’s data lives.

And so, we can decide to store the data for each account wherever we like. A key-value database happens to be a good choice. It does the job of storing the identifier-account pair, while not adding any extra features that are unnecessary for this application (looking at you, relational databases).

Just for reference, the Go Ethereum (GETH) node implementation uses LevelDB as its key/value storage.

So long as the identifiers in our key-value database are used as the paths in the Patricia Merkle trie, we can reconstruct the tree (by hashing node contents), and calculate its root as needed. All is good!

Back to State Representation

Awesome! We have our Patricia Merkle trie, stored in a key-value database, hosted in some nodes in the Blockchain. Leaves in the tree hold account information, which we loosely defined as a set of attributes (also in key-value fashion) a couple minutes ago.

Don’t you feel like something’s missing? Aren’t we forgetting something?

Accounts are not the only things to store — we also need to deal with the data associated with each Smart Contract!

Each Smart Contract defines its own set of rules (we’ll get into that later in the series), and crucially, its own state. Defining this custom state is an art in its own right — but ultimately, we’ll need to store it somewhere. Care to guess how we’ll be storing that information?

You probably guessed it: in another Patricia Merkle trie!

So yeah, every Smart Contract will have its own trie (let’s call it a contract trie) representing its state, and said trie will have a root hash. And we can store this hash in the accounts trie, so that we can quickly check that the information stored in a contract trie has not been altered.

This completes our account representation — we just need to add the storageRoot key, where we’ll save the root hash of a contract trie, in case the account is a contract account:

Click to zoom

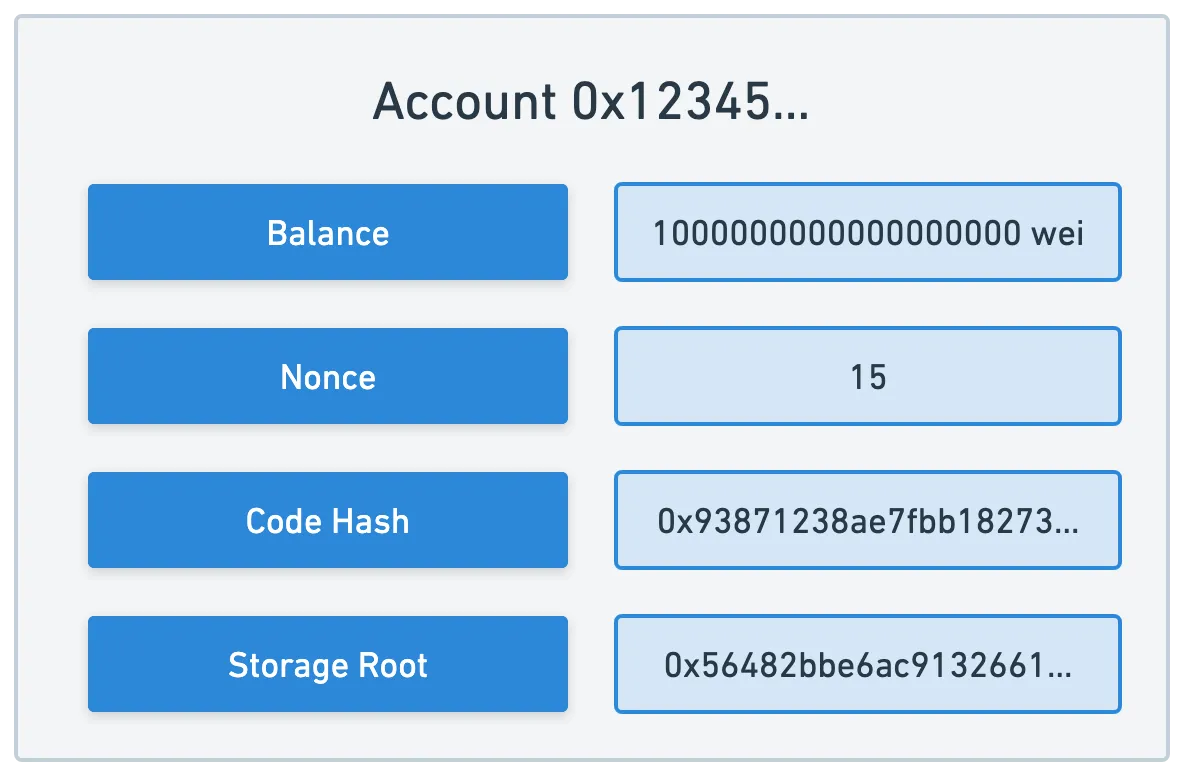
And that’s just about it! Not as mysterious in the end, isn’t it?

Summary

This time around, we’ve discussed the data structures used to store Ethereum’s state.

I think learning about these data structures is not only fun, but it may also prove useful for other applications. Patricia tries are used to solve other types of problems that are totally unrelated to Blockchain, like for example IP address lookups.

I’ve purposely left something important out of the scope of this article. In the case of accounts, we’ve completely defined what is to be “stored” in our Patricia Merkle trie. But what about Smart Contracts?

We haven’t yet addressed how Ethereum’s state is modeled. In other words, we know how to store the data of a Smart Contract, but we don’t really know what we’re storing!

And so, the next step in our adventure will find us working through the operating principles of Smart Contracts — we’ll start by understanding how their state is defined, and then delve into how they receive and handle user interaction (calls). Until the next one!